| Revision as of 21:21, 9 August 2020 edit88.12.136.21 (talk) →Center of mass motion (1st one-body problem)← Previous edit | Latest revision as of 03:40, 2 December 2024 edit undoHellacioussatyr (talk | contribs)Extended confirmed users9,667 edits →Central forcesTag: 2017 wikitext editor | ||
| (44 intermediate revisions by 29 users not shown) | |||
| Line 1: | Line 1: | ||
| {{ |
{{Short description|Motion problem in classical mechanics}} | ||
| {{About|the two-body problem in classical mechanics|the career management problem of working couples|Two-body problem (career)}} | {{About|the two-body problem in classical mechanics|the relativistic version|Two-body problem in general relativity|the career management problem of working couples|Two-body problem (career)}} | ||
| {{multiple image | {{multiple image | ||
| |direction=horizontal | |direction=horizontal | ||
| Line 9: | Line 8: | ||
| |image1=orbit5.gif | |image1=orbit5.gif | ||
| |image2=orbit2.gif | |image2=orbit2.gif | ||
| |footer=''Left: |
|footer='''Left:''' Two bodies of similar ] orbiting a common ] external to both bodies, with ]s. This model is typical of ].<br>'''Right:''' Two bodies with a "slight" difference in mass orbiting a common barycenter. Their sizes and this type of orbit are similar to the ] (in which the barycenter is external to both bodies), as well as the ]–] system (in which the barycenter is internal to the larger body). | ||
| }} | }} | ||
| {{Astrodynamics}} | {{Astrodynamics}} | ||
| In ], the '''two-body problem''' is to predict the motion of two massive objects which are abstractly viewed as ]. The problem assumes that the two objects interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored. | |||
| In ], the '''two-body problem''' is to calculate and predict the motion of two massive bodies that are orbiting each other in space. The problem assumes that the two bodies are ]s that interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored. | |||
| The most prominent case of the classical two-body problem is the ] case (see also ]), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as ], ], and ]. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions. | |||
| The most prominent example of the classical two-body problem is the gravitational case (see also ]), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as ]s, ]s, and ]. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions. | |||
| A simpler "one body" model, the "]", treats one object as the immobile source of a force acting on other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (as with a light planet orbiting a heavy star, where the star can be treated as essentially stationary). | A simpler "one body" model, the "]", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (as with a light planet orbiting a heavy star, where the star can be treated as essentially stationary). | ||
| However, the one-body approximation is usually unnecessary except as a stepping stone. For many forces, including gravitational ones, the general version of the two-body problem can be ], allowing it to be solved completely, and giving a solution simple enough to be used effectively. | However, the one-body approximation is usually unnecessary except as a stepping stone. For many forces, including gravitational ones, the general version of the two-body problem can be ], allowing it to be solved completely, and giving a solution simple enough to be used effectively. | ||
| Line 26: | Line 26: | ||
| === Gravitation and other inverse-square examples === | === Gravitation and other inverse-square examples === | ||
| The two-body problem is interesting in astronomy because pairs of astronomical objects are often moving rapidly in arbitrary directions (so their motions become interesting), widely separated from one another (so they |
The two-body problem is interesting in astronomy because pairs of astronomical objects are often moving rapidly in arbitrary directions (so their motions become interesting), widely separated from one another (so they will not collide) and even more widely separated from other objects (so outside influences will be small enough to be ignored safely). | ||
| Under the force of ], each member of a pair of such objects will orbit their mutual center of mass in an elliptical pattern, unless they are moving fast enough to escape one another entirely, in which case their paths will diverge along other planar ]. If one object is very much heavier than the other, it will move far less than the other with reference to the shared center of mass. The mutual center of mass may even be inside the larger object. | Under the force of ], each member of a pair of such objects will orbit their mutual center of mass in an elliptical pattern, unless they are moving fast enough to escape one another entirely, in which case their paths will diverge along other planar ]s. If one object is very much heavier than the other, it will move far less than the other with reference to the shared center of mass. The mutual center of mass may even be inside the larger object. | ||
| For |
For the derivation of the solutions to the problem, see ] or ]. | ||
| In principle, the same solutions apply to macroscopic problems involving objects interacting not only through gravity, but through any other attractive ] obeying an ], with ] being the obvious physical example. In practice, such problems rarely arise. Except perhaps in experimental apparatus or other specialized equipment, we rarely encounter electrostatically interacting objects which are moving fast enough, and in such a direction, as to avoid colliding, and/or which are isolated enough from their surroundings. | In principle, the same solutions apply to macroscopic problems involving objects interacting not only through gravity, but through any other attractive ] obeying an ], with ] being the obvious physical example. In practice, such problems rarely arise. Except perhaps in experimental apparatus or other specialized equipment, we rarely encounter electrostatically interacting objects which are moving fast enough, and in such a direction, as to avoid colliding, and/or which are isolated enough from their surroundings. | ||
| The dynamical system of a two-body system under the influence of torque turns out to be a ].<ref>{{cite journal |last1=Luo |first1=Siwei |title=The Sturm-Liouville problem of two-body system |journal=Journal of Physics Communications | date=22 June 2020 |volume=4 |issue=6 |page=061001 |doi=10.1088/2399-6528/ab9c30|bibcode=2020JPhCo...4f1001L |doi-access=free }}</ref> | |||
| === Inapplicability to atoms and subatomic particles === | === Inapplicability to atoms and subatomic particles === | ||
| Line 38: | Line 40: | ||
| Although the two-body model treats the objects as point particles, classical mechanics only apply to systems of macroscopic scale. Most behavior of subatomic particles ''cannot'' be predicted under the classical assumptions underlying this article or using the mathematics here. | Although the two-body model treats the objects as point particles, classical mechanics only apply to systems of macroscopic scale. Most behavior of subatomic particles ''cannot'' be predicted under the classical assumptions underlying this article or using the mathematics here. | ||
| ] in an atom are sometimes described as "orbiting" its ], following an ] of ] (this is the source of the term "]"). However, electrons don't actually orbit nuclei in any meaningful sense, and ] are necessary for any useful understanding of the electron's real behavior. Solving the classical two-body problem for an electron orbiting an atomic nucleus is misleading and does not produce many useful insights. | ]s in an atom are sometimes described as "orbiting" its ], following an ] of ] (this is the source of the term "]"). However, electrons don't actually orbit nuclei in any meaningful sense, and ] are necessary for any useful understanding of the electron's real behavior. Solving the classical two-body problem for an electron orbiting an atomic nucleus is misleading and does not produce many useful insights. | ||
| == Reduction to two independent, one-body problems == | == Reduction to two independent, one-body problems == | ||
| {{See also|Classical central-force problem#Relation to the classical two-body problem}} | |||
| {{See also|Kepler problem}} | |||
| {{Duplication|date=June 2019|section=yes|dupe=Classical central-force problem#Relation to the classical two-body problem|note=we keep this article as the primary article for the math part}} | |||
| The complete two-body problem can be solved by re-formulating it as two one-body problems: a trivial one and one that involves solving for the motion of one particle in an external ]. Since many one-body problems can be solved exactly, the corresponding two-body problem can also be solved. | |||
| {{Duplication|date=June 2019|section=yes|dupe=Classical central-force problem#Relation to the classical two-body problem}} | |||
| ] for two-body problem; Jacobi coordinates are <math>\boldsymbol{R}=\frac {m_1}{M} \boldsymbol{x}_1 + \frac {m_2}{M} \boldsymbol{x}_2 </math> and <math>\boldsymbol{r} = \boldsymbol{x}_1 - \boldsymbol{x}_2 </math> with <math>M = m_1+m_2 \ </math>.<ref name=Betounes>{{cite book|title=Differential Equations| author=David Betounes|url=https://archive.org/details/differentialequa0000beto|url-access=registration| isbn=0-387-95140-7 | page=58; Figure 2.15|date=2001|publisher=Springer}}</ref>]] | |||
| The complete two-body problem can be solved by re-formulating it as two one-body problems: a trivial one and one that involves solving for the motion of one particle in an external ]. Since many one-body problems can be solved exactly, the corresponding two-body problem can also be solved. | |||
| Let {{math|'''x'''<sub>1</sub>}} and {{math|'''x'''<sub>2</sub>}} be the vector positions of the two bodies, and ''m''<sub>1</sub> and ''m''<sub>2</sub> be their masses. The goal is to determine the trajectories {{math|'''x'''<sub>1</sub>(''t'')}} and {{math|'''x'''<sub>2</sub>(''t'')}} for all times ''t'', given the initial positions {{math|1='''x'''<sub>1</sub>(''t'' = 0)}} and {{math|1='''x'''<sub>2</sub>(''t'' = 0)}} and the initial velocities {{math|1='''v'''<sub>1</sub>(''t'' = 0)}} and {{math|1='''v'''<sub>2</sub>(''t'' = 0)}}. | |||
| ] for two-body problem; Jacobi coordinates are <math>\boldsymbol{R}=\frac {m_1}{M} \boldsymbol{x}_1 + \frac {m_2}{M} \boldsymbol{x}_2 </math> and <math>\boldsymbol{r} = \boldsymbol{x}_1 - \boldsymbol{x}_2 </math> with <math>M = m_1+m_2 \ </math>.<ref name=Betounes>{{cite book|title=Differential Equations|author=David Betounes|url=https://archive.org/details/differentialequa0000beto|url-access=registration|isbn=0-387-95140-7|page=58; Figure 2.15|date=2001|publisher=Springer}}</ref>]] | |||
| Let '''x'''<sub>1</sub> and '''x'''<sub>2</sub> be the vector positions of the two bodies, and ''m''<sub>1</sub> and ''m''<sub>2</sub> be their masses. The goal is to determine the trajectories '''x'''<sub>1</sub>(''t'') and '''x'''<sub>2</sub>(''t'') for all times ''t'', given the initial positions '''x'''<sub>1</sub>(''t'' = 0) and '''x'''<sub>2</sub>(''t'' = 0) and the initial velocities '''v'''<sub>1</sub>(''t'' = 0) and '''v'''<sub>2</sub>(''t'' = 0). | |||
| When applied to the two masses, ] states that | When applied to the two masses, ] states that | ||
| {{NumBlk||<math display="block">\mathbf{F}_{12}(\mathbf{x}_{1},\mathbf{x}_{2}) = m_{1} \ddot{\mathbf{x}}_{1} </math>|Equation {{EquationRef|1}}}} | |||
| {{NumBlk||<math display="block">\mathbf{F}_{21}(\mathbf{x}_{1},\mathbf{x}_{2}) = m_{2} \ddot{\mathbf{x}}_{2} </math>|Equation {{EquationRef|2}}}} | |||
| :<math> | |||
| \mathbf{F}_{12}(\mathbf{x}_{1},\mathbf{x}_{2}) = m_{1} \ddot{\mathbf{x}}_{1} \quad \quad \quad (\mathrm{Equation} \ 1) | |||
| </math> | |||
| :<math> | |||
| \mathbf{F}_{21}(\mathbf{x}_{1},\mathbf{x}_{2}) = m_{2} \ddot{\mathbf{x}}_{2} \quad \quad \quad (\mathrm{Equation} \ 2) | |||
| </math> | |||
| where '''F'''<sub>12</sub> is the force on mass 1 due to its interactions with mass 2, and '''F'''<sub>21</sub> is the force on mass 2 due to its interactions with mass 1. The two dots on top of the '''x''' position vectors denote their second derivative with respect to time, or their acceleration vectors. | where '''F'''<sub>12</sub> is the force on mass 1 due to its interactions with mass 2, and '''F'''<sub>21</sub> is the force on mass 2 due to its interactions with mass 1. The two dots on top of the '''x''' position vectors denote their second derivative with respect to time, or their acceleration vectors. | ||
| Adding and subtracting these two equations decouples them into two one-body problems, which can be solved independently. ''Adding'' equations (1) and (2) results in an equation describing the ] (]) motion. By contrast, ''subtracting'' equation (2) from equation (1) results in an equation that describes how the vector '''r''' |
Adding and subtracting these two equations decouples them into two one-body problems, which can be solved independently. ''Adding'' equations (1) and ({{EquationNote|2}}) results in an equation describing the ] (]) motion. By contrast, ''subtracting'' equation (2) from equation (1) results in an equation that describes how the vector {{math|1='''r''' = '''x'''<sub>1</sub> − '''x'''<sub>2</sub>}} between the masses changes with time. The solutions of these independent one-body problems can be combined to obtain the solutions for the trajectories {{math|'''x'''<sub>1</sub>(''t'')}} and {{math|'''x'''<sub>2</sub>(''t'')}}. | ||
| === Center of mass motion (1st one-body problem) === | === Center of mass motion (1st one-body problem) === | ||
| Let <math>\mathbf{R} </math> be the position of the ] (]) of the system. Addition of the force equations (1) and (2) yields | Let <math>\mathbf{R} </math> be the position of the ] (]) of the system. Addition of the force equations (1) and (2) yields | ||
| <math display="block">m_1 \ddot{\mathbf{x}}_1 + m_2 \ddot{\mathbf{x}}_2 = (m_1 + m_2)\ddot{\mathbf{R}} = \mathbf{F}_{12} + \mathbf{F}_{21} = 0</math> | |||
| where we have used ] {{math|1='''F'''<sub>12</sub> = −'''F'''<sub>21</sub>}} and where | |||
| :<math> | |||
| <math display="block">\ddot{\mathbf{R}} \equiv \frac{m_{1}\ddot{\mathbf{x}}_{1} + m_{2}\ddot{\mathbf{x}}_{2}}{m_{1} + m_{2}}.</math> | |||
| </math> | |||
| where we have used ] '''F'''<sub>12</sub> = −'''F'''<sub>21</sub> and where | |||
| :<math> | |||
| \ddot{\mathbf{R}} \equiv \frac{m_{1}\ddot{\mathbf{x}}_{1} + m_{2}\ddot{\mathbf{x}}_{2}}{m_{1} + m_{2}}. | |||
| </math> | |||
| The resulting equation: | The resulting equation: | ||
| <math display="block">\ddot{\mathbf{R}} = 0</math> | |||
| shows that the velocity <math>\mathbf{v} = \frac{dR}{dt}</math> of the center of mass is constant, from which follows that the total momentum {{math|''m''<sub>1</sub> '''v'''<sub>1</sub> + ''m''<sub>2</sub> '''v'''<sub>2</sub>}} is also constant (]). Hence, the position {{math|'''R'''(''t'')}} of the center of mass can be determined at all times from the initial positions and velocities. | |||
| :<math> | |||
| \ddot{\mathbf{R}} = 0 | |||
| </math> | |||
| shows that the velocity <math> | |||
| {\mathbf{v}}= {dR \over dt} | |||
| </math> of the center of mass is constant, from which follows that the total momentum ''m''<sub>1</sub> '''v'''<sub>1</sub> + ''m''<sub>2</sub> '''v'''<sub>2</sub> is also constant (]). Hence, the position '''R''' (''t'') of the center of mass can be determined at all times from the initial positions and velocities. | |||
| ===Displacement vector motion (2nd one-body problem)=== | ===Displacement vector motion (2nd one-body problem)=== | ||
| Dividing both force equations by the respective masses, subtracting the second equation from the first, and rearranging gives the equation | Dividing both force equations by the respective masses, subtracting the second equation from the first, and rearranging gives the equation | ||
| <math display="block"> | |||
| :<math> | |||
| \ddot {\mathbf{r}} = \ddot{\mathbf{x}}_{1} - \ddot{\mathbf{x}}_{2} = | \ddot {\mathbf{r}} = \ddot{\mathbf{x}}_{1} - \ddot{\mathbf{x}}_{2} = | ||
| \left( \frac{\mathbf{F}_{12}}{m_{1}} - \frac{\mathbf{F}_{21}}{m_{2}} \right) = | \left( \frac{\mathbf{F}_{12}}{m_{1}} - \frac{\mathbf{F}_{21}}{m_{2}} \right) = | ||
| \left(\frac{1}{m_{1}} + \frac{1}{m_{2}} \right)\mathbf{F}_{12} | \left(\frac{1}{m_{1}} + \frac{1}{m_{2}} \right)\mathbf{F}_{12} | ||
| </math> | </math> | ||
| where we have again used ] {{math|1='''F'''<sub>12</sub> = −'''F'''<sub>21</sub>}} and where {{math|'''r'''}} is the ] from mass 2 to mass 1, as defined above. | |||
| The force between the two objects, which originates in the two objects, should only be a function of their separation {{math|'''r'''}} and not of their absolute positions {{math|'''x'''<sub>1</sub>}} and {{math|'''x'''<sub>2</sub>}}; otherwise, there would not be ], and the laws of physics would have to change from place to place. The subtracted equation can therefore be written: | |||
| where we have again used ] '''F'''<sub>12</sub> = −'''F'''<sub>21</sub> and where '''r''' is the ] from mass 2 to mass 1, as defined above. | |||
| <math display="block">\mu \ddot{\mathbf{r}} = \mathbf{F}_{12}(\mathbf{x}_{1},\mathbf{x}_{2}) = \mathbf{F}(\mathbf{r})</math> | |||
| The force between the two objects, which originates in the two objects, should only be a function of their separation '''r''' and not of their absolute positions '''x'''<sub>1</sub> and '''x'''<sub>2</sub>; otherwise, there would not be ], and the laws of physics would have to change from place to place. The subtracted equation can therefore be written: | |||
| :<math> | |||
| \mu \ddot{\mathbf{r}} = \mathbf{F}_{12}(\mathbf{x}_{1},\mathbf{x}_{2}) = \mathbf{F}(\mathbf{r}) | |||
| </math> | |||
| where <math>\mu</math> is the ''']''' | where <math>\mu</math> is the ''']''' | ||
| <math display="block">\mu = \frac{1}{\frac{1}{m_1} + \frac{1}{m_2}} = \frac{m_1 m_2}{m_1 + m_2}.</math> | |||
| Solving the equation for {{math|'''r'''(''t'')}} is the key to the two-body problem. The solution depends on the specific force between the bodies, which is defined by <math>\mathbf{F}(\mathbf{r})</math>. For the case where <math>\mathbf{F}(\mathbf{r})</math> follows an ], see the ]. | |||
| :<math> | |||
| \mu = \frac{1}{\frac{1}{m_1} + \frac{1}{m_{2}}} = \frac{m_1 m_2}{m_1 + m_2}. | |||
| </math> | |||
| Solving the equation for '''r'''(''t'') is the key to the two-body problem. The solution depends on the specific force between the bodies, which is defined by <math>\mathbf{F}(\mathbf{r})</math>. For the case where <math>\mathbf{F}(\mathbf{r})</math> follows an ], see the ]. | |||
| Once '''R''' (''t'') and '''r'''(''t'') have been determined, the original trajectories may be obtained | |||
| :<math> | |||
| \mathbf{x}_1(t) = | |||
| \mathbf{R} (t) + \frac{m_2}{m_1 + m_2} \mathbf{r}(t) | |||
| </math> | |||
| :<math> | |||
| \mathbf{x}_2(t) = | |||
| \mathbf{R} (t) - \frac{m_{1}}{m_1 + m_2} \mathbf{r}(t) | |||
| </math> | |||
| Once {{math|'''R'''(''t'')}} and {{math|'''r'''(''t'')}} have been determined, the original trajectories may be obtained | |||
| <math display="block">\mathbf{x}_1(t) = \mathbf{R} (t) + \frac{m_2}{m_1 + m_2} \mathbf{r}(t)</math> | |||
| <math display="block">\mathbf{x}_2(t) = \mathbf{R} (t) - \frac{m_1}{m_1 + m_2} \mathbf{r}(t)</math> | |||
| as may be verified by substituting the definitions of '''R''' and '''r''' into the right-hand sides of these two equations. | as may be verified by substituting the definitions of '''R''' and '''r''' into the right-hand sides of these two equations. | ||
| == Two-body motion is planar == | == Two-body motion is planar == | ||
| The motion of two bodies with respect to each other always lies in a plane (in the ]). |
The motion of two bodies with respect to each other always lies in a plane (in the ]). | ||
| Proof: Defining the ] '''p''' and the ] '''L''' of the system, with respect to the center of mass, by the equations | Proof: Defining the ] {{math|'''p'''}} and the ] {{math|'''L'''}} of the system, with respect to the center of mass, by the equations | ||
| <math display="block">\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{r} \times \mu \frac{d\mathbf{r}}{dt},</math> | |||
| where {{mvar|μ}} is the ] and {{math|'''r'''}} is the relative position {{math|'''r'''<sub>2</sub> − '''r'''<sub>1</sub>}} (with these written taking the center of mass as the origin, and thus both parallel to {{math|'''r'''}}) the rate of change of the angular momentum {{math|'''L'''}} equals the net ] {{math|'''N'''}} | |||
| :<math> | |||
| \mathbf{L} = \mathbf{r} \times \mathbf{ |
<math display="block">\mathbf{N} = \frac{d\mathbf{L}}{dt} = \dot{\mathbf{r}} \times \mu\dot{\mathbf{r}} + \mathbf{r} \times \mu\ddot{\mathbf{r}} \ ,</math> | ||
| and using the property of the ] that {{math|1='''v''' × '''w''' = '''0'''}} for any vectors {{math|'''v'''}} and {{math|'''w'''}} pointing in the same direction, | |||
| </math> | |||
| <math display="block"> \mathbf{N} \ = \ \frac{d\mathbf{L}}{dt} = \mathbf{r} \times \mathbf{F} \ ,</math> | |||
| where μ is the ] and '''r''' is the relative position '''r<sub>2</sub>'''-'''r<sub>1</sub>''' (with these written taking the center of mass as the origin, and thus both parallel to '''r''') the rate of change of the angular momentum '''L''' equals the net ] '''N''' | |||
| with {{math|1='''F''' = ''μ'' ''d''{{i sup|2}}'''r'''/''dt''{{i sup|2}}}}. | |||
| Introducing the assumption (true of most physical forces, as they obey ]) that the force between two particles acts along the line between their positions, it follows that {{math|1='''r''' × '''F''' = '''0'''}} and the ] (conserved). Therefore, the displacement vector {{math|'''r'''}} and its velocity {{math|'''v'''}} are always in the plane ] to the constant vector {{math|'''L'''}}. | |||
| :<math> | |||
| \mathbf{N} = \frac{d\mathbf{L}}{dt} = \dot{\mathbf{r}} \times \mu\dot{\mathbf{r}} + \mathbf{r} \times \mu\ddot{\mathbf{r}} \ , | |||
| </math> | |||
| and using the property of the ] that '''v''' × '''w''' = '''0''' for any vectors '''''v''''' and '''''w''''' pointing in the same direction, | |||
| :<math> | |||
| \mathbf{N} \ = \ \frac{d\mathbf{L}}{dt} = \mathbf{r} \times \mathbf{F} \ , | |||
| </math> | |||
| with '''F''' = ''μ d''<sup> 2</sup>'''r''' /''dt''<sup> 2</sup>. | |||
| Introducing the assumption (true of most physical forces, as they obey ]) that the force between two particles acts along the line between their positions, it follows that '''r''' × '''F''' = '''0''' and the ] (conserved). Therefore, the displacement vector '''r''' and its velocity '''v''' are always in the plane ] to the constant vector '''L'''. | |||
| == Energy of the two-body system == | == Energy of the two-body system == | ||
| If the force '''F'''('''r''') is ] then the system has a ] ''U''('''r'''), so the total ] can be written as | If the force {{math|'''F'''('''r''')}} is ] then the system has a ] {{math|''U''('''r''')}}, so the total ] can be written as | ||
| <math display="block">E_\text{tot} = \frac{1}{2} m_1 \dot{\mathbf{x}}_1^2 + \frac{1}{2} m_2 \dot{\mathbf{x}}_2^2 + U(\mathbf{r}) = \frac{1}{2} (m_1 + m_2) \dot{\mathbf{R}}^2 + {1 \over 2} \mu \dot{\mathbf{r}}^2 + U(\mathbf{r})</math> | |||
| In the center of mass frame the ] is the lowest and the total energy becomes | In the center of mass frame the ] is the lowest and the total energy becomes | ||
| <math display="block">E = \frac{1}{2} \mu \dot{\mathbf{r}}^2 + U(\mathbf{r})</math> | |||
| The coordinates '''x'''<sub>1</sub> and '''x'''<sub>2</sub> can be expressed as | The coordinates {{math|'''x'''<sub>1</sub>}} and {{math|'''x'''<sub>2</sub>}} can be expressed as | ||
| <math display="block"> \mathbf{x}_1 = \frac{\mu}{m_1} \mathbf{r}</math> | |||
| <math display="block"> \mathbf{x}_2 = - \frac{\mu}{m_2} \mathbf{r}</math> | |||
| and in a similar way the energy ''E'' is related to the energies ''E''<sub>1</sub> and ''E''<sub>2</sub> that separately contain the kinetic energy of each body: | and in a similar way the energy ''E'' is related to the energies {{math|''E''<sub>1</sub>}} and {{math|''E''<sub>2</sub>}} that separately contain the kinetic energy of each body: | ||
| <math display="block">\begin{align} | |||
| :<math> | |||
| E_1 & = \frac{\mu}{m_1} E = \frac{1}{2} m_1 \dot{\mathbf{x}}_1^2 + \frac{\mu}{m_1} U(\mathbf{r}) \\ | |||
| \begin{align} | |||
| E_2 & = \frac{\mu}{m_2} E = \frac{1}{2} m_2 \dot{\mathbf{x}}_2^2 + \frac{\mu}{m_2} U(\mathbf{r}) \\ | |||
| E_2 & = \frac{\mu}{m_2}E = {1 \over 2} m_2 \dot{\mathbf{x}}_2^2 + \frac{\mu}{m_2} U(\mathbf{r}) \\ | |||
| E_\text{tot} & = E_1 + E_2 | E_\text{tot} & = E_1 + E_2 | ||
| \end{align} | \end{align}</math> | ||
| </math> | |||
| == Central forces == | == Central forces == | ||
| {{main|Classical central-force problem}} | {{main|Classical central-force problem}} | ||
| For many physical problems, the force '''F'''('''r''') is a ], i.e., it is of the form | For many physical problems, the force {{math|1='''F'''('''r''')}} is a ], i.e., it is of the form | ||
| <math display="block">\mathbf{F}(\mathbf{r}) = F(r)\hat{\mathbf{r}}</math> | |||
| where {{math|1=''r'' = {{abs|'''r'''}}}} and {{math|1='''r̂''' = '''r'''/''r''}} is the corresponding ]. We now have: | |||
| :<math>\mathbf{F}(\mathbf{r}) = F(r)\hat{\mathbf{r}}</math> | |||
| <math display="block">\mu \ddot{\mathbf{r}} = {F}(r) \hat{\mathbf{r}} \ ,</math> | |||
| where ''r'' = |'''r'''| and '''r̂''' = '''r'''/''r'' is the corresponding ]. We now have: | |||
| where {{math|''F''(''r'')}} is negative in the case of an attractive force. | |||
| :<math> | |||
| \mu \ddot{\mathbf{r}} = {F}(r) \hat{\mathbf{r}} \ , | |||
| </math> | |||
| where ''F''(''r'') is negative in the case of an attractive force. | |||
| ==See also== | ==See also== | ||
| Line 190: | Line 139: | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | * ] | ||
| * ] | |||
| * ] | |||
| * ] | * ] | ||
| Line 205: | Line 151: | ||
| * {{cite book | author = Landau LD | author-link = Lev Landau | author2 = Lifshitz EM | author2-link = Evgeny Lifshitz | date = 1976 | title = Mechanics | edition = 3rd. | publisher = ] | location = New York | isbn = 0-08-029141-4 | url-access = registration | url = https://archive.org/details/mechanics00land }} | * {{cite book | author = Landau LD | author-link = Lev Landau | author2 = Lifshitz EM | author2-link = Evgeny Lifshitz | date = 1976 | title = Mechanics | edition = 3rd. | publisher = ] | location = New York | isbn = 0-08-029141-4 | url-access = registration | url = https://archive.org/details/mechanics00land }} | ||
| * {{cite book | author = Goldstein H | author-link = Herbert Goldstein | date = 1980 | title = ] | edition = 2nd. | publisher = ] | location = New York | isbn = 0-201-02918-9}} | * {{cite book | author = Goldstein H | author-link = Herbert Goldstein | date = 1980 | title = ] | edition = 2nd. | publisher = ] | location = New York | isbn = 0-201-02918-9}} | ||
| == External links == | == External links == | ||
| * at ] | * at ] | ||
| {{Authority control}} | |||
| {{DEFAULTSORT:Two-Body Problem}} | {{DEFAULTSORT:Two-Body Problem}} | ||
| ] | |||
| ] | ] | ||
| ] | ] | ||
Latest revision as of 03:40, 2 December 2024
Motion problem in classical mechanics This article is about the two-body problem in classical mechanics. For the relativistic version, see Two-body problem in general relativity. For the career management problem of working couples, see Two-body problem (career).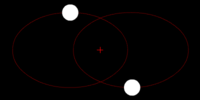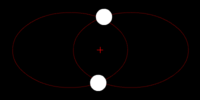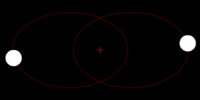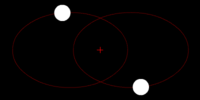
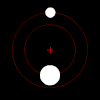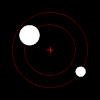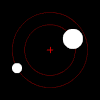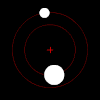 Left: Two bodies of similar mass orbiting a common barycenter external to both bodies, with elliptic orbits. This model is typical of binary stars.
Left: Two bodies of similar mass orbiting a common barycenter external to both bodies, with elliptic orbits. This model is typical of binary stars.Right: Two bodies with a "slight" difference in mass orbiting a common barycenter. Their sizes and this type of orbit are similar to the Pluto–Charon system (in which the barycenter is external to both bodies), as well as the Earth–Moon system (in which the barycenter is internal to the larger body).
| Part of a series on |
| Astrodynamics |
|---|
| Orbital mechanics |
| Orbital elements |
|
Types of two-body orbits by eccentricity Transfer orbit |
| Equations |
| Celestial mechanics |
| Gravitational influences |
| N-body orbitsLagrangian points |
| Engineering and efficiency |
| Preflight engineering |
| Efficiency measures |
| Propulsive maneuvers |
In classical mechanics, the two-body problem is to calculate and predict the motion of two massive bodies that are orbiting each other in space. The problem assumes that the two bodies are point particles that interact only with one another; the only force affecting each object arises from the other one, and all other objects are ignored.
The most prominent example of the classical two-body problem is the gravitational case (see also Kepler problem), arising in astronomy for predicting the orbits (or escapes from orbit) of objects such as satellites, planets, and stars. A two-point-particle model of such a system nearly always describes its behavior well enough to provide useful insights and predictions.
A simpler "one body" model, the "central-force problem", treats one object as the immobile source of a force acting on the other. One then seeks to predict the motion of the single remaining mobile object. Such an approximation can give useful results when one object is much more massive than the other (as with a light planet orbiting a heavy star, where the star can be treated as essentially stationary).
However, the one-body approximation is usually unnecessary except as a stepping stone. For many forces, including gravitational ones, the general version of the two-body problem can be reduced to a pair of one-body problems, allowing it to be solved completely, and giving a solution simple enough to be used effectively.
By contrast, the three-body problem (and, more generally, the n-body problem for n ≥ 3) cannot be solved in terms of first integrals, except in special cases.
Results for prominent cases
Gravitation and other inverse-square examples
The two-body problem is interesting in astronomy because pairs of astronomical objects are often moving rapidly in arbitrary directions (so their motions become interesting), widely separated from one another (so they will not collide) and even more widely separated from other objects (so outside influences will be small enough to be ignored safely).
Under the force of gravity, each member of a pair of such objects will orbit their mutual center of mass in an elliptical pattern, unless they are moving fast enough to escape one another entirely, in which case their paths will diverge along other planar conic sections. If one object is very much heavier than the other, it will move far less than the other with reference to the shared center of mass. The mutual center of mass may even be inside the larger object.
For the derivation of the solutions to the problem, see Classical central-force problem or Kepler problem.
In principle, the same solutions apply to macroscopic problems involving objects interacting not only through gravity, but through any other attractive scalar force field obeying an inverse-square law, with electrostatic attraction being the obvious physical example. In practice, such problems rarely arise. Except perhaps in experimental apparatus or other specialized equipment, we rarely encounter electrostatically interacting objects which are moving fast enough, and in such a direction, as to avoid colliding, and/or which are isolated enough from their surroundings.
The dynamical system of a two-body system under the influence of torque turns out to be a Sturm-Liouville equation.
Inapplicability to atoms and subatomic particles
Although the two-body model treats the objects as point particles, classical mechanics only apply to systems of macroscopic scale. Most behavior of subatomic particles cannot be predicted under the classical assumptions underlying this article or using the mathematics here.
Electrons in an atom are sometimes described as "orbiting" its nucleus, following an early conjecture of Niels Bohr (this is the source of the term "orbital"). However, electrons don't actually orbit nuclei in any meaningful sense, and quantum mechanics are necessary for any useful understanding of the electron's real behavior. Solving the classical two-body problem for an electron orbiting an atomic nucleus is misleading and does not produce many useful insights.
Reduction to two independent, one-body problems
See also: Classical central-force problem § Relation to the classical two-body problem See also: Kepler problem| This section duplicates the scope of other articles, specifically Classical central-force problem#Relation to the classical two-body problem. Please discuss this issue and help introduce a summary style to the section by replacing the section with a link and a summary or by splitting the content into a new article. (June 2019) |
The complete two-body problem can be solved by re-formulating it as two one-body problems: a trivial one and one that involves solving for the motion of one particle in an external potential. Since many one-body problems can be solved exactly, the corresponding two-body problem can also be solved.

Let x1 and x2 be the vector positions of the two bodies, and m1 and m2 be their masses. The goal is to determine the trajectories x1(t) and x2(t) for all times t, given the initial positions x1(t = 0) and x2(t = 0) and the initial velocities v1(t = 0) and v2(t = 0).
When applied to the two masses, Newton's second law states that
| Equation 1 |
| Equation 2 |
where F12 is the force on mass 1 due to its interactions with mass 2, and F21 is the force on mass 2 due to its interactions with mass 1. The two dots on top of the x position vectors denote their second derivative with respect to time, or their acceleration vectors.
Adding and subtracting these two equations decouples them into two one-body problems, which can be solved independently. Adding equations (1) and (2) results in an equation describing the center of mass (barycenter) motion. By contrast, subtracting equation (2) from equation (1) results in an equation that describes how the vector r = x1 − x2 between the masses changes with time. The solutions of these independent one-body problems can be combined to obtain the solutions for the trajectories x1(t) and x2(t).
Center of mass motion (1st one-body problem)
Let be the position of the center of mass (barycenter) of the system. Addition of the force equations (1) and (2) yields where we have used Newton's third law F12 = −F21 and where
The resulting equation: shows that the velocity of the center of mass is constant, from which follows that the total momentum m1 v1 + m2 v2 is also constant (conservation of momentum). Hence, the position R(t) of the center of mass can be determined at all times from the initial positions and velocities.
Displacement vector motion (2nd one-body problem)
Dividing both force equations by the respective masses, subtracting the second equation from the first, and rearranging gives the equation where we have again used Newton's third law F12 = −F21 and where r is the displacement vector from mass 2 to mass 1, as defined above.
The force between the two objects, which originates in the two objects, should only be a function of their separation r and not of their absolute positions x1 and x2; otherwise, there would not be translational symmetry, and the laws of physics would have to change from place to place. The subtracted equation can therefore be written: where is the reduced mass
Solving the equation for r(t) is the key to the two-body problem. The solution depends on the specific force between the bodies, which is defined by . For the case where follows an inverse-square law, see the Kepler problem.
Once R(t) and r(t) have been determined, the original trajectories may be obtained as may be verified by substituting the definitions of R and r into the right-hand sides of these two equations.
Two-body motion is planar
The motion of two bodies with respect to each other always lies in a plane (in the center of mass frame).
Proof: Defining the linear momentum p and the angular momentum L of the system, with respect to the center of mass, by the equations
where μ is the reduced mass and r is the relative position r2 − r1 (with these written taking the center of mass as the origin, and thus both parallel to r) the rate of change of the angular momentum L equals the net torque N and using the property of the vector cross product that v × w = 0 for any vectors v and w pointing in the same direction,
with F = μ dr/dt.
Introducing the assumption (true of most physical forces, as they obey Newton's strong third law of motion) that the force between two particles acts along the line between their positions, it follows that r × F = 0 and the angular momentum vector L is constant (conserved). Therefore, the displacement vector r and its velocity v are always in the plane perpendicular to the constant vector L.
Energy of the two-body system
If the force F(r) is conservative then the system has a potential energy U(r), so the total energy can be written as
In the center of mass frame the kinetic energy is the lowest and the total energy becomes The coordinates x1 and x2 can be expressed as and in a similar way the energy E is related to the energies E1 and E2 that separately contain the kinetic energy of each body:
Central forces
Main article: Classical central-force problemFor many physical problems, the force F(r) is a central force, i.e., it is of the form where r = |r| and r̂ = r/r is the corresponding unit vector. We now have: where F(r) is negative in the case of an attractive force.
See also
- Energy drift
- Equation of the center
- Euler's three-body problem
- Kepler orbit
- Kepler problem
- n-body problem
- Three-body problem
- Virial theorem
References
- Luo, Siwei (22 June 2020). "The Sturm-Liouville problem of two-body system". Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30.
- David Betounes (2001). Differential Equations. Springer. p. 58; Figure 2.15. ISBN 0-387-95140-7.
Bibliography
- Landau LD; Lifshitz EM (1976). Mechanics (3rd. ed.). New York: Pergamon Press. ISBN 0-08-029141-4.
- Goldstein H (1980). Classical Mechanics (2nd. ed.). New York: Addison-Wesley. ISBN 0-201-02918-9.
 and
and  with
with  .
.

 be the position of the
be the position of the  where we have used
where we have used 
 shows that the velocity
shows that the velocity  of the center of mass is constant, from which follows that the total momentum m1 v1 + m2 v2 is also constant (
of the center of mass is constant, from which follows that the total momentum m1 v1 + m2 v2 is also constant ( where we have again used
where we have again used  where
where  is the
is the 
 . For the case where
. For the case where 
 as may be verified by substituting the definitions of R and r into the right-hand sides of these two equations.
as may be verified by substituting the definitions of R and r into the right-hand sides of these two equations.

 and using the property of the
and using the property of the  with F = μ dr/dt.
with F = μ dr/dt.

 The coordinates x1 and x2 can be expressed as
The coordinates x1 and x2 can be expressed as

 and in a similar way the energy E is related to the energies E1 and E2 that separately contain the kinetic energy of each body:
and in a similar way the energy E is related to the energies E1 and E2 that separately contain the kinetic energy of each body:

 where r = |r| and r̂ = r/r is the corresponding
where r = |r| and r̂ = r/r is the corresponding  where F(r) is negative in the case of an attractive force.
where F(r) is negative in the case of an attractive force.