| Revision as of 00:31, 25 December 2023 view sourceDVdm (talk | contribs)Autopatrolled, Extended confirmed users, New page reviewers, Pending changes reviewers, Rollbackers138,503 edits Reverting edit(s) by Bera678 (talk) to rev. 1144070767 by DVdm: Personal attack towards another editor (WP:NPA) (RW 16.1)Tags: RW Undo← Previous edit |
Revision as of 06:29, 7 December 2024 view source Jonesey95 (talk | contribs)Autopatrolled, Extended confirmed users, Page movers, Mass message senders, Template editors378,696 edits Fix high-priority Linter errors. I hope you don't mind this minor cleanup edit in your user space.Next edit → |
| Line 11: |
Line 11: |
|
On page 230 in to , Dingle writes: |
|
On page 230 in to , Dingle writes: |
|
: (start quote) |
|
: (start quote) |
|
::<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; border-radius: 10px; background-color: {{{color|#fff7f7}}};"> |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; border-radius: 10px; background-color: {{{color|#fff7f7}}};"> |
|
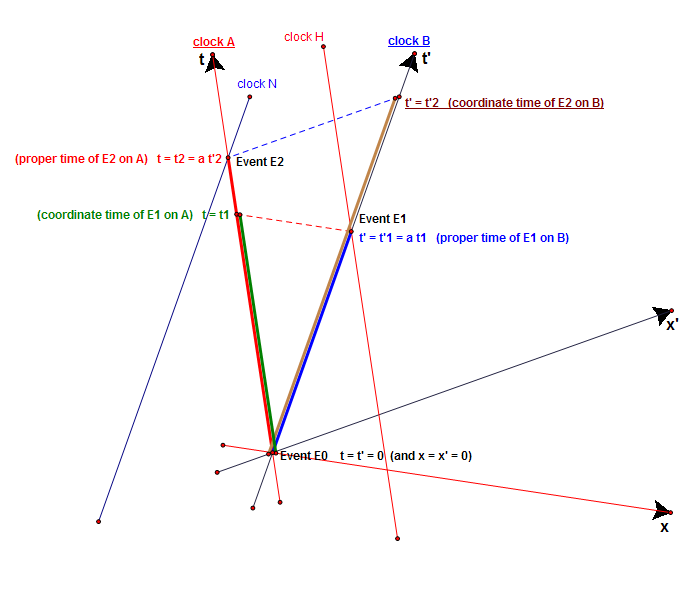
:::: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{ForestGreen}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
:::: {{!xt|Thus, between events E0 and E1, A advances by <math>\color{ForestGreen}{t_1}</math> and B by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
::::: <math>\frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
::::: <math>\frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
| Line 22: |
Line 22: |
|
Dingle should have written as follows: |
|
Dingle should have written as follows: |
|
: (start correction) |
|
: (start correction) |
|
::<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; border-radius: 10px; background-color: {{{color|#f7fff7}}};"> |
|
<div style="padding: 1em; border: solid 3px {{{bordercolor|#a08040}}}; border-radius: 10px; background-color: {{{color|#f7fff7}}};"> |
|
:::: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{ForestGreen}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
:::: {{xt|Thus, between events E0 and E1, A, which is '''not present''' at both events, advances by <math>\color{ForestGreen}{t_1}</math> and B, which is '''present''' at both events, by <math>\color{Blue}{t'_1 = a t_1}</math> by (1). Therefore}} |
|
::::: <math>\frac{\color{ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{ForestGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
|
::::: <math>\frac{\color{ForestGreen}{\text{rate of clock not present at both events E0 and E1}}}{\color{Blue}{\text{rate of clock present at both events E0 and E1}}} = \frac{\color{ForestGreen}{\text{coordinate time of E1}}}{\color{Blue}{\text{proper time of E1}}} = \frac{\color{ForestGreen}{\text{rate of A}}}{\color{Blue}{\text{rate of B}}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{t'_1}} = \frac{\color{ForestGreen}{t_1}}{\color{Blue}{a t_1}} = \frac{1}{a} > 1 \qquad \text{(3)}</math> |
| Line 28: |
Line 28: |
|
:::: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
|
:::: {{xt|Thus, between events E0 and E2, B, which is '''not present''' at both events, advances by <math>\color{Brown}{t'_2}</math> and A, which is '''present''' at both events, by <math>\color{Red}{t_2 = a t'_2}</math> by (2). Therefore}} |
|
::::: <math>\frac{\color{Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color{Red}{\text{rate of clock present at both events E0 and E2}}} = \frac{\color{Brown}{\text{coordinate time of E2}}}{\color{Red}{\text{proper time of E2}}} = \frac{\color{Brown}{\text{rate of B}}}{\color{Red}{\text{rate of A}}} = \frac{\color{Brown}{t'_2}}{\color{Red}{t_2}} = \frac{\color{Brown}{t'_2}}{\color{Red}{a t'_2}} = \frac{1}{a} > 1 \qquad \text{(4)}</math> |
|
::::: <math>\frac{\color{Brown}{\text{rate of clock not present at both events E0 and E2}}}{\color{Red}{\text{rate of clock present at both events E0 and E2}}} = \frac{\color{Brown}{\text{coordinate time of E2}}}{\color{Red}{\text{proper time of E2}}} = \frac{\color{Brown}{\text{rate of B}}}{\color{Red}{\text{rate of A}}} = \frac{\color{Brown}{t'_2}}{\color{Red}{t_2}} = \frac{\color{Brown}{t'_2}}{\color{Red}{a t'_2}} = \frac{1}{a} > 1 \qquad \text{(4)}</math> |
|
:::: {{xt|'''Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time:<p>hence there is no reason to say that the theory requiring them must be false.'''}} |
|
:::: {{xt|'''Equations (3) and (4) are consistent and say that any event's coordinate time is always larger than its proper time:'''<p>'''hence there is no reason to say that the theory requiring them must be false.'''</p>}} |
|
</div> |
|
</div> |
|
: (end correction) |
|
: (end correction) |
 and B by
and B by  by (1). Therefore
by (1). Therefore

 and A by
and A by  by (2). Therefore
by (2). Therefore


