| Revision as of 09:20, 5 April 2009 editOli Filth (talk | contribs)Extended confirmed users, Pending changes reviewers, Rollbackers18,040 edits Reverted 1 edit by 59.184.160.59; Self-redirect. (TW)← Previous edit | Revision as of 15:07, 6 April 2009 edit undoJbolden1517 (talk | contribs)5,334 edits science apologist version.... Major Major revision see User_talk:Durova for contextNext edit → | ||
| Line 2: | Line 2: | ||
| {{For|the book by Sir Isaac Newton|Opticks}} | {{For|the book by Sir Isaac Newton|Opticks}} | ||
| ].]] | |||
| {{Nofootnotes|date=March 2009}} | |||
| '''Optics''' is the study of the behavior and properties of ], including its ] with ] and its ] by ].<ref name=McGrawHill>{{cite book|title=McGraw-Hill Encyclopedia of Science and Technology|edition=5th edition|publisher=The McGraw-Hill Companies, Inc.|date=1993}}</ref> The word ''optics'' comes from the ] word ''{{polytonic|ὀπτική}}'', meaning ''appearance'' or ''look''.<ref>{{cite book|title=The Concise Oxford Dictionary of English Etymology |date=1996 |author=T. F. HOAD}}</ref> | |||
| ]'']] | |||
| Optics usually describes the behavior of ] light and the behavior of ] and ] light, which are similar to visible light but are not detectable by the naked human eye. Other phenomena such as ]s, ]s, and ] waves can be described with optical principles because all of these, along with visible light, are types of ].<ref name=McGrawHill /> During the nineteenth century the physicist ] discovered that light is a type of ]; since that time optics has largely been regarded as a sub-field of ] within ]. | |||
| '''Optics''' is the study of the behavior and properties of ] including its ] with ] and its ] by ].<ref name=McGrawHill>{{cite book|title=McGraw-Hill Encyclopedia of Science and Technology|edition=5th edition|publisher=The McGraw-Hill Companies, Inc.|date=1993}}</ref> The word ''optics'' comes from ''{{polytonic|ὀπτική}}'', meaning ''appearance'' or ''look'' in ].<ref>{{citebook|title=The Concise Oxford Dictionary of English Etymology |date=1996 |author=T. F. HOAD}}</ref> | |||
| ] can be used to describe most everyday optical phenomena. It is usually simpler to use one of the two broad simplifying assumptions for describing light: to treat light as a ] or as a ]. '']'', developed in the 16th and 17th century, treats light as a collection of rays that travel in straight lines unless they are bent through ]. '']'' was developed in the 19th century and accounts for the wave-like<!--Perhaps this could be changed, but wave-nature didn't seem right to me. --> nature of light, which is needed in particular to explain ] and ]. | |||
| Optics usually describes the behavior of ], ], and ] light; however because light is an ], similar phenomena occur in ]s, ]s, ] waves, and other forms of ] and analogous phenomena occur with ] beams.<ref name=McGrawHill /> Since the discovery by ] that light is electromagnetic radiation, optics has largely been regarded in ] as a sub-field of ]. Some optical phenomena depend on the ] nature of light relating some areas of optics to ]. In practice, the vast majority of optical phenomena can be accounted for using the classical electromagnetic description of light, as described by ], resorting to phenomenological rules (e.g. Beer's Law, constitutive equations) to describe the interaction of light with matter. Even when still completely classical, complete electromagnetic descriptions of optical behavior are often difficult to apply to practical problems. This is why particular simplified models are used instead, notably those of ] and ]. These limited models adequately describe large subsets of optical phenomena while ignoring behavior that is insignificant for the system of interest.<ref name=McGrawHill /> | |||
| Together, geometrical and physical optics encompass ''classical optics'', a system of models capable of describing and predicting many optical phenomena. However, in certain situations, more modern approaches must be used for accurate predictions and explanations. In particular, observations that light behaves ] were first correctly explained in the early twentieth century when ] replaced classical electromagnetism. ] deals with the best model of light scientists have developed to date: the ]. | |||
| The pure science of optics is called optical science or ] to distinguish it from applied optical sciences, which are referred to as ]. Prominent subfields of optical engineering include ], ], and ]. Some of these fields overlap, with nebulous boundaries between the subjects terms that mean slightly different things in different parts of the world and in different areas of industry.<ref>{{cite web|title=SPIE society|url=http://spie.org/}}</ref> A professional community of researchers in ] has developed in the last several decades due to advances in ].<ref>{{cite book|title=The principles of nonlinear optics|author=Shen, Y. R.|publisher=New York, Wiley-Interscience|date=1984}} | |||
| </ref> | |||
| Optical science is relevant to and studied in many related disciplines including ], ], and ] (particularly ] and ]). | Optical science is relevant to and studied in many related disciplines including ], ], ], and ] (particularly ] and ]). Practical applications of optics are found in a variety of technologies and everyday objects, including ]s, ]es, ]s, ]s, ]s, and ]. | ||
| ==History== | ==History== | ||
| ]'s manuscript showing his discovery of the law of refraction, now known as ].]] | |||
| {{main|History of optics}} | {{main|History of optics}} | ||
| Optics began with the development of ] by the ]ians and ]ns, followed by theories on ] and ] developed by ancient ] and ] philosophers, and the development of ] in the ]. The earliest known ] were made from polished ], often ], and have been dated as early as 700 BC for ]n lenses such as the Layard/]<ref> </ref>. The ]s and Greeks filled glass ]s with water to make lenses. | |||
| {{Expand-section|date=March 2009}} | |||
| ] (c. 801–873) was one of the earliest important writers on optics in the ]. In a work known in the west as ''De radiis stellarum'', al-Kindi first articulated ], something not accepted in Europe for another 800 years.<ref>Cited in D. C. Lindberg, ''Theories of Vision from al-Kindi to Kepler'', (Chicago: Univ. of Chicago Pr., 1976), p. 19.</ref> This theory of the active power of rays had an influence on later Western scholars such as as ] and ].<ref>{{citation|first=David C.|last=Lindberg|journal=]|volume=62|issue=4|date=Winter 1971|pages=469–489 |doi=10.1086/350790|title=Alkindi's Critique of Euclid's Theory of Vision}}</ref> In 984, the ], ] wrote a treatise "On Burning Mirrors and Lenses", correctly describing a law of ] mathematically equivalent to ].<ref>R. Rashed, "A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses", '']'' 81 (1990): 464–91.</ref> He used his law of refraction to compute the shapes of lenses and mirrors that focus light at a single point on the axis. In the early eleventh century, ] wrote his '']'', which extensively documented the then-current Islamic understanding of optics; it included the first descriptions of the optical phenomena associated with ] and ],<ref name=Wade>{{Harv|Wade|Finger|2001}}</ref><ref name=Elliott>{{Harv|Elliott|1966|Chapter 1}}</ref> having great influence in the later development of the modern telescope.<ref>O. S. Marshall (1950). "Alhazen and the Telescope", ''Astronomical Society of the Pacific Leaflets'' '''6''', p. 4.</ref> | |||
| In the thirteenth century, ], inspired by Ibn al-Haytham, used parts of glass spheres as ]es and discovered that light reflects from objects rather than being released from them. In Italy, around 1284, ] invented the first wearable eye ].<ref>{{cite web |last=Bellis |first=Mary |title=The History of Eye Glasses or Spectacles |work=About.com:Inventors |url=http://inventors.about.com/od/gstartinventions/a/glass_3.htm |accessdate=2007-09-01}}</ref> The first rudimentary telescopes were developed independently in the 1570s and 1580s by ],<ref></ref> ]<ref name=Topdemir>{{citation|first=Hüseyin Gazi|last=Topdemir|title=Takîyüddîn'in Optik Kitabi|publisher=Ministry of Culture Press, ]|year=1999}}</ref> and ].<ref>Giambattista della Porta, (2005), ''Natural Magick'', page 339. NuVision Publications, LLC.</ref> | |||
| The earliest known working telescopes were ]s, a type which rely entirely on lenses for magnification. Their development in the ] in 1608 was by three individuals: ] and ], who were spectacle makers in Middelburg, and ] of ]. In Italy, ] greatly improved upon these designs the following year. ] constructed the first ] in 1616, which incorporated a mirror to improve magnification. In 1668, ] designed an improved reflecting telescope that bears his name, the ].<ref></ref> | |||
| The first microscope was made around 1595 in ].<ref>, Nobel Foundation, retrieved April 3, 2009 </ref> Three different ] makers have been given credit for the invention: ] (who also developed the first real ]); ]; and his son, ]. The coining of the name "microscope" has been credited to ], who gave that name to Galileo's compound microscope in 1625.<ref>Stephen Jay Gould(2000). The Lying Stones of Marrakech, ch.2 "The Sharp-Eyed Lynx, Outfoxed by Nature". London: Jonathon Cape. ISBN 0224050443</ref> | |||
| Optical theory progressed in the mid-seventeenth century with ] written by ], which explained a variety of optical phenomena including reflection and refraction by assuming that light was ] by objects which produced it.<ref name=Sabra>{{cite book|title=Theories of light, from Descartes to Newton|author=A. I. Sabra|publisher=CUP Archive|date=1981|isbn=0521284368}}</ref> This differed substantively from ancient Greek notions that light emanated from the ]. In the late 1660s and early 1670s, Newton expanded Descartes' ideas into a ], famously showing that white light, instead of being a unique color, was a really composite of different colors that can be separated into a ] with a ]. In 1690, ] proposed a ] for light based on suggestions that had been made by ] in 1664. Hooke himself publicly criticized Newton's theories of light; the feud between the two lasted until Hooke's death. In 1704, Newton published '']'' and, at the time, partly because of his success in other areas of physics, was generally considered to be the victor in the debate over the nature of light.<ref name=Sabra /> | |||
| Newtonian optics and emission theory was generally accepted as correct until the early nineteenth century when ] and ] conducted experiments in the ] of light that firmly established light's wave-nature. Young's famous ] showed that light followed the ], something normal particles do not follow. This experiment lead to a theory of ] for light and opened an entire theory of ],<ref>{{cite book|last=Magie|first=William Francis|title=A Source Book in Physics|publisher=Harvard University Press|year=1935}} p. 309</ref> This was the optical theory that was successfully unified with ] by James Clerk Maxwell in the 1860s.<ref> James Clerk Maxwell, '']'', Philosophical Transactions of the Royal Society of London 155, 459-512 (1865).</ref> | |||
| The next development in optical theory came in 1899 when ] correctly modeled ] by assuming that the exchange of energy between light and matter only occurred in discrete amounts he called ''quanta''.<ref name="Kragh">For a solid approach to the complexity of Planck's intellectual motivations for the quantum, for his reluctant acceptance of its implications, see Helge Kragh, , ''Physics World''. December 2000.</ref> In 1905, ] published the theory of the ] that firmly established the quantization of light itself.<ref>{{Citation | |||
| |last=Einstein|first=Albert|year=1905a | |||
| |title=On a Heuristic Viewpoint Concerning the Production and Transformation of Light | |||
| |journal=Annalen der Physik|volume=17|pages=132–148 | |||
| |url=http://lorentz.phl.jhu.edu/AnnusMirabilis/AeReserveArticles/eins_lq.pdf | |||
| }}. This annus mirabilis paper on the photoelectric effect was received by Annalen der Physik 18 March.</ref> In 1913, ] showed that atoms could only emit discrete amounts of energy, thus explaining the discrete lines seen in ] and ].<ref>1913. "" ''Philosophical Magazine'' 26 (Series 6): 1-25. The landmark paper laying the ] and ]ing.</ref> The understanding of the interaction between light and ], which followed from these developments, not only formed the basis of quantum optics but also was crucial for the ] of ] as a whole. | |||
| ] gained practical importance with the invention of the ] in 1953 and the ] in 1960.<ref>{{cite book |last=Taylor |first=Nick |title=LASER: The inventor, the Nobel laureate, and the thirty-year patent war |year=2000 |publisher=Simon & Schuster |location=New York |isbn=0-684-83515-0 }}</ref> Following the work of ] in ], ], ], and ] applied quantum theory to the electromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the ] of light. The ultimate culmination was the theory of ], which explains all optics and electromagnetic processes in general as being the result of the exchange of real and ] ]s.<ref>{{cite book |last=Feynman |first=Richard |authorlink=Richard Feynman |date=1985 |url=http://www.amazon.com/gp/reader/0691024170 |title=QED: The Strange Theory of Light and Matter |chapter=Chapter 1 |page=6 |publisher=Princeton University Press}}</ref> | |||
| == Classical optics == | == Classical optics == | ||
| ] propagates through ] as a ] with ]s, ]s, ], and ]s that are unique to how it was ] and the particular conditions of the material through which it is propagating.]] | |||
| Classical optics works by ] light as an electromagnetic ] composed of ] ] and ]s. These fields generate each other according to ] as the wave propagates through ] and oscillates in ].<ref>Maxwell, ''A Dynamical Theory of the Electromagnetic Field'', 1864 '''5''', page 499.</ref> | |||
| Before ] became important, optics consisted mainly of the application of classical electromagnetism and its ]s to light. Classical optics divides into two main branches: geometric optics and ]. | |||
| The ] of light waves is determined by the ] of the oscillations of the emitter. While the frequency of a light wave does not normally change as light transmits through different materials, called ], the wavelength of light is affected by the ] in different media. Since the speed (''v'') of any wave is related by the formula | |||
| ''Geometric optics'', or ''ray optics'', describes ] ] in terms of "]". Rays are bent at the ] between two dissimilar media, and may be curved in a ] in which the ] is a function of position. The "ray" in geometric optics is an ], or "]," which is perpendicular to the ]s of the actual optical waves (therefore collinear with the wave vector). Geometric optics provides rules for propagating these rays through an optical system, which indicates how the actual wavefront will propagate. This is a significant simplification of optics, and fails to account for many important optical effects such as ] and ]. It is a good approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging, including ]s. | |||
| :<math>v=\lambda \nu</math> | |||
| Geometric optics is often simplified even further by making the ], or "small angle approximation." The mathematical behavior then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of ] and ''paraxial raytracing'', which are used to find first-order properties of optical systems, such as approximate image and object positions and magnifications. | |||
| ] is an expansion of paraxial optics that provides a more accurate model of coherent radiation like ] beams. While still using the paraxial approximation, this technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics. | |||
| where <math>\lambda</math> is the wavelength and <math>\nu</math> is the frequency of the wave, a changing wavelength results in a changing ] of light.<ref>{{cite book | title = In Quest of the Universe | author = Theo Koupelis and Karl F. Kuhn | publisher = Jones & Bartlett Publishers | year = 2007 | isbn = 0763743879 | url = http://books.google.com/books?id=WwKjznJ9Kq0C&pg=PA102&dq=wavelength+lambda+light+sound+frequency+wave+speed&lr=&as_brr=3&ei=nfIpSazAMIzukgSP04nODg }}</ref> This can be characterized with by the index of refraction, a unitless number defined as | |||
| ''Physical optics'' or ] builds on ] and models the propagation of complex wavefronts through optical systems, including both the ] and the ] of the wave. This technique, which is usually applied numerically on a computer, can account for diffraction, ], and polarization effects, as well as other complex effects. Approximations are still generally used, however, so this is not a full electromagnetic wave theory model of the propagation of light. Such a full model is much more computationally demanding, but can be used to solve small-scale problems that require this more accurate treatment. | |||
| :<math>n=c/v</math> | |||
| === Topics related to classical optics === | |||
| where ''c'' is the ] -- a ] value equal to 299,792,458 ].<ref name=Delphenich> | |||
| {{Col-begin}} | |||
| {{cite journal |title=Nonlinear optical analogies in quantum electrodynamics |url=http://arxiv.org/abs/hep-th/0610088v1 |author=D. H. Delphenich |year=2006 |journal=ArXiv preprint}}</ref> | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ** ]s | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * Geometric optics of: | |||
| ** ] | |||
| ** ]s | |||
| ** ]s | |||
| ** ] | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| ** ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| ** ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| ] in a ].]] | |||
| The ] of the light wave is related to the ] of the light which is related to the ] stored in the electric and magnetic fields of the light wave. | |||
| {{Col-end}} | |||
| Before ] became important, optics consisted mainly of the application of classical electromagnetism and its ]s to light. Classical optics divides into two main branches: ] and ]. | |||
| ===Geometrical optics=== | |||
| {{main|Geometrical optics}} | |||
| ] in ]. In this image, each maximum amplitude ] is marked with a ] to illustrate the ]. The ] is the arrow ] to these ] surfaces.]] | |||
| ''Geometrical optics'', or ''ray optics'', describes ] ] in terms of "]". The "ray" in geometric optics is an ], or "]", that can be used to predict the path of light. A light ray is a a ] that is ] to a ]s of a ] (therefore ] with the ]). Light rays bend at the ] between two dissimilar media, and may be curved in a ] in which the ] changes. Geometrical optics provides rules for propagating these rays through an optical system, which indicates how the actual wavefront will propagate. This is a significant simplification of optics that fails to account for optical effects such as ] and ]. It is a good approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging, including ]s. | |||
| A slightly more rigorous definition of a light ray follows from ] which states that ''the path taken between two points by a ray of light is the path that can be traversed in the least time.''<ref>Arthur Schuster, ''An Introduction to the Theory of Optics'', London: Edward Arnold, 1904 .</ref> | |||
| ====Approximations==== | |||
| Geometric optics is often simplified even further by making the ], or "small angle approximation." The mathematical behavior then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of ] and ''paraxial ]'', which are used to find basic properties of optical systems, such as approximate ] and object positions and ]s.<ref name=Greivenkamp>{{cite book | first=John E. | last=Greivenkamp | year=2004 | title=Field Guide to Geometrical Optics | publisher=SPIE | others=SPIE Field Guides vol. '''FG01''' | isbn=0-8194-5294-7 |pages=19–20 }}</ref> | |||
| The ] is an expansion of paraxial optics that provides a more accurate model of coherent radiation like ] beams. While still using the paraxial approximation, this technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics.<ref>{{cite book | first = Anthony E.|last=Siegman|year=1986|title=Lasers|publisher=University Science Books|isbn= 0-935702-11-3}} Chapter 16.</ref> | |||
| ====Reflections==== | |||
| {{main|reflection}} | |||
| ] | |||
| Reflections can be divided into two types: ] and ]. In diffuse reflection, the wavefronts do not maintain paraxiality due to imperfections in the reflecting surface. Modeling of diffuse reflection can only be done in a statistical, average sense, generally characterized by an ] that indicates a certain amount of light intensity is lost during the reflection due to ].<ref name="PhysicsWorld"></ref> | |||
| Specular reflection, in comparison, occurs when the wavefronts maintain paraxiality due to reflection off of a ]. This allows for production of coherent images that can be associated with an actual (]) or extrapolated (]) location in space. An incident ray meets a surface at an angle with respect to ] called the ] (<math>\theta_i</math>) and reflects off the surface at an angle with respect to normal called the ] (<math>\theta_r</math>). The law of reflection states | |||
| :<math>\theta_i=\theta_r</math>.<ref name=Geoptics>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0201529815}}Chapter 35</ref> | |||
| For ], the law of reflection implies that the images of objects are upright and the same distance behind the mirror as the distance that objects are in front of the mirror and the image size is the same as the object size (i.e. the ] of a flat mirror is unity). The law also implies that ]s are ] (i.e. left and right are interchanged). ]s can be used to create reflections that are not parity inverted and also ].<ref name=Geoptics /> | |||
| ] can be modeled by ] and using the law of reflection at each point of the ] to surface. For ] surfaces, the parallel rays incident on the mirror will all converge at a ]. Other curved surfaces will also exhibit a focal point with aberrations due to the diverging shape causing the focal point to be smeared out in space. The most famous example of this is the so-called ]. The images of objects seen in a curved mirror follow the ] which relates the object distance (<math>d_o</math>) and image distances (<math>d_i</math>) to the focal length (<math>f</math>): | |||
| :<math>\frac{1}{d_o}+ \frac{1}{d_i} = \frac{1}{f}</math>.<ref name=Geoptics /> | |||
| The ] of a mirror is defined as the height of the image divided by the height of the object: | |||
| :<math>m \equiv \frac{h_i}{h_o} = - \frac{d_i}{d_o}</math>. | |||
| The negative sign in this equation is used as a ]. By convention, if the magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down). Upright images in mirrors are virtual images while inverted images are real and can be ] onto a screen.<ref name=Geoptics /> | |||
| ====Refractions==== | |||
| {{main|Refraction}} | |||
| ] | |||
| Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is a simple interface between one medium with index of refraction <math>n_1</math> and another medium with index of refraction <math>n_2</math>. In such situations, ] describes the resulting deflection of the light ray: | |||
| :<math>n_1\sin\theta_1 = n_2\sin\theta_2\ </math> | |||
| where <math>\theta_1</math> and <math>\theta_2</math> are the angles between the normal (to the interface) plane and the incident waves respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies: | |||
| :<math>v_1\sin\theta_2\ = v_2\sin\theta_1</math> | |||
| where <math>v_1</math> and <math>v_2</math> are the wave velocities through the respective media.<ref name=Geoptics /> | |||
| Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called ] and allows for ] technology. Another refraction scenario of note is the situation where the refracted ray and the reflected ray form a ]. The angle of incidence required for such a scenario is known as ] and results in the production of ].<ref name=Geoptics /> | |||
| Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a ] results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce ] ] that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to ].<ref name=Geoptics /> | |||
| Some media have an index of refraction which changes and, thus, light rays end up curving through the medium rather than traveling in straight lines. This effect is what is responsible for ]s seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a changing index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including ] and ]. The phenomenon is studied in the field of ].<ref>E. W. Marchand, Gradient Index Optics, New York, NY, Academic Press, 1978.</ref> | |||
| ] | |||
| A device which produces converging or diverging light rays due to refraction is known as a ]. Thin lenses produce focal points on either side that can be modeled using the ].<ref name=hecht>{{cite book | first=Eugene|last=Hecht|year=1987|title=Optics|edition=2nd ed.|publisher=Addison Wesley|isbn=0-201-11609-X}} Chapters 5 & 6.</ref> In general, two types of lenses exist: ]es which cause parallel light rays to converge and ]es which cause parallel light rays to diverge. The detail prediction of how images are produced in these lenses can be made using ray-tracing similar to curved mirrors. Also similar to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length (<math>f</math>) and object distance (<math>S_1</math>): | |||
| :<math>\frac{1}{S_1} + \frac{1}{S_2} = \frac{1}{f} </math> | |||
| where <math>S_2</math> is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.<ref name=hecht /> | |||
| Likewise, the magnification of a lens is given by | |||
| :<math> M = - \frac{S_2}{S_1} = \frac{f}{f - S_1} </math> | |||
| where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.<ref name=Geoptics /> | |||
| Lenses suffer from ] that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light (]).<ref name=Geoptics /> | |||
| ====Optical instruments==== | |||
| ]'']] | |||
| {{main|optical instruments}} | |||
| Single lenses have a variety of applications including ]es, ]es, and ]es while single mirrors are used in ]s and ]s. Combining a number of mirrors, prisms, and lenses produces compound optical instruments which have practical uses. For example, a ] is simply two plane mirrors aligned to allow for viewing around obstructions. The most famous compound optical instruments in science are the ] and the ] which were both invented by the Dutch in the late 16th century.<ref name=instrument>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0201529815}}Chapter 36</ref> | |||
| Microscopes were first developed with just two lenses: an ] and an ]. The objective lens is essentially a ] and was designed with a very small focal length while the eyepieces generally has longer focal lengths. This has the effect of producing magnified images of close objects. Generally, an additional source of illumination is used since magnified images are dimmer due to the ] and the spreading of light rays over a larger surface area. Modern microscopes, known as ''compound microscopes'' have many lenses in them (typically four) to optimize the functionality and enhance image stability.<ref name=instrument /> A slightly different variety of microscope, the ], looks at side-by-side images to produce a ] ] view that appears three dimensional when used by humans.<ref name=nikonstereo1> by Paul E. Nothnagle, William Chambers, and Michael W. Davidson, ''] MicroscopyU''.</ref> | |||
| The first telescopes, called '']s'' were also developed with a single objective and eyepiece lens. In contrast to the microscope, the objective lens of the telescope was designed with a large focal length to avoid optical aberrations. The objective focuses an image of an object that is essentially at ] at its focal point which is adjusted to be at the focal point of an eyepiece which is generally of a much smaller focal length. The main goal of a telescope is not necessarily magnification, but rather collection of light which is determined by the physical size of the objective lens. Thus, telescopes are normally indicated by the diameters of their objectives rather than by the magnification which can be changed by switching eyepieces. Because the magnification of a telescope is equal to the focal length of the objective divided by the focal length of the eyepiece, smaller focal-legnth eyepieces cause greater magnification.<ref name=instrument /> | |||
| Since crafting large lenses is much more difficult than crafting large mirrors, most modern telescopes are '']s'', that is, telescopes that use a primary mirror rather than an objective lens. The same general optical considerations apply to reflecting telescopes that applied to refracting telescopes, namely, the larger the primary mirror, the more light collected ad the magnification is still equal to the focal length of the primary mirror divided by the focal length of the eyepiece. Professional class telescopes generally do not have eyepieces and instead place an instrument (often a ]) at the focal point instead.<ref name=instrument /> | |||
| ===Physical optics=== | |||
| {{main|Physical optics}} | |||
| ''Physical optics'' or ] builds on ] which states that every point on an advancing wavefront is the center of a new disturbance. When combined with the ], this allows for an explanation of how optical phenomena are manifested when there are multiple sources or obstructions that are spaced at similar size as the wavelength of the light.<ref name=phyoptics>Longhurst RS, Geometrical and Physical Optics, 2nd Edition, 1968, Longmans </ref> | |||
| Complex models based on physical optics can account for the propagation of any wavefront through an optical system, including the ], ], and ] of the wave.<ref name=phyoptics /> Additionally, all of the results from geometrical optics can be recovered using the techniques of ] which apply many of the same mathematical and analytical techniques used in ] and ]. Using ] on a computer, optical scientists can account for most ], ], and ] effects, as well as other complex ] patterns. Physical optics still relies on approximations, however, so this is not a full electromagnetic wave theory model of the propagation of light. Such a full model is much more computationally demanding and is normally only used to solve small-scale problems that require more accurate treatments.<ref name=Fourier>{{cite book |first=Joseph|last=Goodman|year=2005|title=Introduction to Fourier Optics|edition=3rd ed,|publisher=Roberts & Co Publishers|isbn=0974707724}} or online </ref> | |||
| ====Superposition and interference==== | |||
| {{main|superposition principle|interference}} | |||
| The ] can be used to predict the precise shape of interacting waveforms through the simple addition of the disturbances. The resulting wave pattern is generally termed "]" and can result in a variety of outcomes. If two waves of the same wavelength and frequency are in ], then the ] align with other crests and wave troughs align with other troughs. This results in ] and an increase in the amplitude of the wave, which for light is associated with a brightening of the waveform in that location. Alternatively, if the two waves of the same wavelength and frequency are out of phase, then the wave crests will align with wave troughs and vice-versa. This results in ] and a decrease in the amplitude of the wave, which for light is associated with a dimming of the waveform at that location. See below for an illustration of this effect.<ref name=interference>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0201529815}}Chapter 37</ref> | |||
| {| | |||
| |- | |||
| | '''combined<br> waveform''' | |||
| | colspan="2" rowspan="3" | ] | |||
| |- | |||
| | '''wave 1''' | |||
| |- | |||
| | '''wave 2''' | |||
| |- | |||
| | <br> | |||
| | '''Two waves in phase''' | |||
| | '''Two waves 180° out <br>of phase''' | |||
| |} | |||
| Since Huygens's principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns.<ref name=interference /> ] is the science of measuring these patterns, usually as a means of making precise determinations of distances or ]s.<ref name=interferometry>{{cite book|last=Hariharan|first=P.|title=Optical Interferometry|edition=2nd edition|publisher=]|place=]|year=2003|url=http://www.astro.lsa.umich.edu/~monnier/Publications/ROP2003_final.pdf}}</ref> The ] was a famously used interference effects to accurately measure the speed of light.<ref>Earl R. Hoover, ''Cradle of Greatness: National and World Achievements of Ohio’s Western Reserve'' (Cleveland: Shaker Savings Association, 1977).</ref> | |||
| ] | |||
| The appearance of ] is directly affected by interference effects. Nonreflective coatings have an index of refraction less than the material on which they are deposited. Such coatings minimize glare and can eliminate a large amount of unwanted reflection. If the thin film has a thickness that is one fourth the wavelength of incident light, the reflected wave from the top of the film and the reflected wave from the film/material interface will be exactly 180 degrees out-of-phase causing destructive interference. Since this can only be done for one particular wavelength, usually a wavelength associated with yellow-green (<math>\lambda = 550</math>nm) where the ] is the brightest is chosen. Alternatively, if the thin-film coating has an index of refraction greater than than the material on which it is deposited, then the reflected wave from the top of the film and the reflected wave from the film/material interface will be in phase when the film has a thickness of one fourth a wavelength. Such optical coatings are used for ]s on ] visors and for color separation in ] cameras. This interference effect is also what causes the colorful rainbow patterns seen in oil slicks.<ref name=interference /> | |||
| ====Diffraction and optical resolution==== | |||
| {{main|diffraction|optical resolution}} | |||
| ] | |||
| ] is the process by which light interference is most commonly observed. The effect was first described in 1665 by ] who also coined the term diffraction, from the Latin ''diffringere'', 'to break into pieces', referring to light breaking up into different directions.<ref>{{cite book | title = Memoires pour l'histoire des sciences et des beaux arts | author = Jean Louis Aubert | publisher = Impr. de S. A. S.; Chez E. Ganeau| location = Paris | year = 1760 | pages = 149 | url = http://books.google.com/books?vid=OCLC58901501&id=3OgDAAAAMAAJ&pg=PP151&lpg=PP151&dq=grimaldi+diffraction+date:0-1800&as_brr=1 }}</ref><ref>{{cite book | title = A Treatise on Optics | author = Sir David Brewster | year = 1831 | publisher = Longman, Rees, Orme, Brown & Green and John Taylor | location = London | pages = 95 | url = http://books.google.com/books?vid=OCLC03255091&id=opYAAAAAMAAJ&pg=RA1-PA95&lpg=RA1-PA95&dq=grimaldi+diffraction+date:0-1840&as_brr=1 }}</ref> Later that century, Robert Hooke and Isaac Newton also described phenomena now known to be diffraction in ]<ref>Robert Hooke. "Micrographia: or, Some physiological descriptions of minute bodies made by magnifying glasses". London: J. Martyn and J. Allestry, 1665. (first edition).</ref> while ] recorded his observations of diffraction patterns from bird feathers.<ref>{{cite journal | author = Turnbull, H. W. | title = Early Scottish Relations with the Royal Society: I. James Gregory, F.R.S. (1638–1675) | journal = Notes and Records of the Royal Society of London | year = 1940–1941 | volume = 3 | pages = 22 – 38 | url = http://www.jstor.org/sici?sici=0035-9149(194004%2F194109)3%3C22%3AESRWTR%3E2.0.CO%3B2-D&cookieSet=1}}</ref> | |||
| The first physical optics model of diffraction that relied on Huygen's Principle was developed in 1803 by ] in his accounts of the interference patterns of from two closely spaced slits. Explaining his results by interference of the waves emanating from the two different slits, he deduced that light must propagate as waves.<ref>{{cite book|last =Rothman|first =Tony|authorlink =Tony Rothman|title =Everything's Relative and Other Fables in Science and Technology |publisher =Wiley|location =New Jersey|date =2003|isbn =0471202576}}</ref> ] did more definitive studies and calculations of diffraction, published in 1815 and 1818.<ref name=hecht /> | |||
| The simplest physical models of diffraction use by equations that describe the angular separation of light and dark fringes due to light of a particular wavelength (<math>\lambda</math>). In general, the equation takes the form | |||
| :<math>m \lambda = d \sin \theta</math> | |||
| where <math>d</math> is the separation between two wavefront sources (in the case of Young's experiments, it was ]), <math>\theta</math> is the angular separation between the central fringe and the <math>m</math>th order fringe, where the central maximum is <math>m = 0</math>.<ref name=diffraction>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0201529815}}Chapter 38</ref> | |||
| This equation is modified slightly to take into account a variety of situations such diffraction through a single gap, diffraction through multiple slits, or diffraction through a ] that contains a large number of slits at equal spacing.<ref name=diffraction /> More complicated models of diffraction require working with the mathematics of ] or ].<ref name=phyoptics /> | |||
| ] makes use of the fact that atoms in a ] have regular spacing at distances that are on the order of one ]. To see diffraction patterns, ]s with similar wavelengths to that spacing are passed through the crystal. Since crystals are three-dimensional objects rather than two dimensional gratings, the associated diffraction pattern varies in two directions according to ] with the associated bright spots occurring in ] and <math>d</math> being twice the spacing between atoms.<ref name=diffraction /> | |||
| Diffraction effects limit the ability for an optical detector to ] separate light sources. In general, light that is passing through an ] will experience diffraction and the best images that can be created (so-called ]) appear as acentral spot with surrounding bright rings, separated by dark nulls; this pattern is known as an ], and the central bright lobe as an ].<ref name=hecht /> The size of such a disk is given by | |||
| :<math> \sin \theta = 1.22 \frac{\lambda}{D}</math> | |||
| where ''θ'' is the angular resolution, ''λ'' is the ] of light, and ''D'' is the ] of the lens aperture. If the angular separation of the two points is significantly less than the Airy disk angular radius, then the two points cannot be resolved in the image, but if their angular separation is much greater than this, distinct images of the two points are formed and they can therefore be resolved. ] defined the somewhat arbitrary "]" that two points whose angular separation is equal to the Airy disk radius to first null can be considered to be resolved. It can be seen that the greater the diameter of the lens or its aperture, the finer the resolution.<ref name=diffraction /> Inteferometry, with its ability to mimic extremely large baseline aperatures, allows for the greatest angular resolution possible.<ref name=interferometry /> | |||
| For astronomical imaging, the atmosphere prevents optimal resolution from being achieved in the visible spectrum due to the atmospheric ] and ] which cause stars to ]. Astronomers refer to this effect as the quality of ]. Techniques known as ] have been utilized to eliminate the atmospheric disruption of images and achieve results that approach the diffraction limit.<ref>'' by Robert Nigel Tubbs</ref> | |||
| ====Dispersion and scattering==== | |||
| ] through a ].]] | |||
| {{main|Dispersion (optics)|Scattering}} | |||
| Refractive processes take place in the physical optics limit as a kind of ]. The simplest type of scattering is ] which occurs when electromagnetic waves are deflected by single particles. In the limit of Thompson scattering, light is dispersed independent of the frequency, in contrast to ] which is frequency-dependent and strictly a ] process. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as ] while the similar process for scattering by particles that are similar or larger in wavelength is known as ] with the ] being a commonly observed result. ] occurs in situations where the frequency changes due to excitation of atoms and molecules and ] occurs when the frequency of light changes due to local changes and movements of a dense material.<ref>{{cite book |last= Bohren |first= Craig F.|coauthors= Donald R. Huffman |title=Absorption and Scattering of Light by Small Particles |publisher= ] |year= 1983 |isbn= 0-471-29340-7 }}</ref> | |||
| Dispersion occurs when different frequencies of light have different ] due to either material differences (material dispersion) or due to the geometry of an optical ] (waveguide dispersion). The most commonly observed dispersion observed is due to the fact that for visible light, most transparent materials (e.g. glasses) have: | |||
| :<math>1 < n(\lambda_{\rm red}) < n(\lambda_{\rm green}) < n(\lambda_{\rm blue})\ ,</math> | |||
| or alternatively: | |||
| :<math>\frac{{\rm d}n}{{\rm d}\lambda} < 0,</math> | |||
| that is, refractive index ''n'' decreases with increasing wavelength λ. In this case, the medium is said to have ''normal dispersion''. Whereas, if the index increases with increasing wavelength the medium has ''anomalous dispersion''.<ref name=Geoptics /> | |||
| At the interface of such a material with air or vacuum (index of ~1), Snell's law predicts that light incident at an angle θ to the ] will be refracted at an angle arcsin( sin (θ) / ''n'') . Thus, blue light, with a higher refractive index, will be bent more strongly than red light, resulting in the well-known ] pattern.<ref name=Geoptics /> | |||
| ] in ] groups. The red dot moves with the ], and the green dots propagate with the ]. In this case, the phase velocity is twice the group velocity. The red dot overtakes two green dots, when moving from the left to the right of the figure. This has the effect of spreading the individual frequencies (which travel with the phase velocity) apart from the wave packet (which travels with the group velocity). Lower frequency waves spread at a slower rate than higher frequency waves, resulting in a spreading of the spectrum from high frequency being the most deflected to low frequency being the least deflected.]] | |||
| Material dispersion is characterized by the ] which relates the refractive index of the material to how it changes as a function of frequency. Waveguide dispersion is dependent on how the ] of the situation changes.<ref name=hecht /> Both kinds of dispersion cause changes in the ] of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified as a group dispersion delay parameter: | |||
| :<math>D = \frac{1}{v_g^2} \frac{dv_g}{d\lambda}</math> | |||
| where <math>v_g</math> is the ].<ref name=optnet>Rajiv Ramaswami and Kumar N. Sivarajan, ''Optical Networks: A Practical Perspective'' (Academic Press: London 1998).</ref> For a uniform medium, the group velocity is | |||
| :<math>v_g = c \left( n - \lambda \frac{dn}{d\lambda} \right)^{-1}</math> | |||
| where ''n'' is the index of refraction and ''c'' is the speed of light in a vacuum.<ref>Brillouin, Léon. ''Wave Propagation and Group Velocity''. Academic Press Inc., New York (1960)</ref> This gives a simpler form for the dispersion delay parameter: | |||
| :<math>D = - \frac{\lambda}{c} \, \frac{d^2 n}{d \lambda^2}.</math> | |||
| If ''D'' is less than zero, the medium is said to have ''positive dispersion''. If ''D'' is greater than zero, the medium has ''negative dispersion''. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes ''positively ]ed'', or ''up-chirped'', increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously dispersive medium, high frequency components travel faster than the lower ones, and the pulse becomes ''negatively ]ed'', or ''down-chirped'', decreasing in frequency with time.<ref>{{cite book | |||
| | last = Born | |||
| | first = Max | |||
| | authorlink = Max Born | |||
| | last2 = Wolf | |||
| | first2 = Emil | |||
| | title = Principle of Optics | |||
| | publisher = ] | |||
| | date = October 1999 | |||
| | location = Cambridge | |||
| | pages = 14–24 | |||
| | isbn = 0521642221}}</ref> | |||
| The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on ]s, since if dispersion is too high, a group of pulses representing will spread in time and merge together, making it impossible to extract the signal.<ref name=optnet /> | |||
| ====Polarization==== | |||
| {{main|Polarization}} | |||
| ] is a general property of waves that describes the orientation of their ]s. For ]s such as many electromagnetic waves, it describes the orientation of the oscillations in the plane perpendicular to the wave's direction of travel. The oscillations may be oriented in a single direction (]), or the oscillation direction may rotate as the wave travels (] or ]). Circularly polarized waves can rotate rightward or leftward in the direction of travel, and which of those two rotations is present in a wave is called the wave's ].<ref name=light>{{cite book|title=University Physics 8e|author=Hugh D. Young|publisher=Addison-Wesley|date=1992|isbn=0201529815}}Chapter 34</ref> | |||
| The typical way to consider polarization is to keep track of the orientation of the electric field ] as the electromagnetic wave propagates. The electric field vector of a plane wave may be arbitrarily divided into two perpendicular ] labeled ''x'' and ''y'' (with '''z''' indicating the direction of travel). The shape traced out in the x-y plane by the electric field vector is a ] that describes the ''polarization state''.<ref name=hecht /> The following figures show some examples of the evolution of the electric field vector (blue), with time (the vertical axes), at a particular point in space, along with its ''x'' and ''y'' components (red/left and green/right), and the path traced by the vector in the plane (purple): The same evolution would occur when looking at the electric field at a particular time while evolving the point in space, along the direction opposite to propagation. | |||
| <div style="float:left;width:170px"> | |||
| ] | |||
| <center>''Linear''</center> | |||
| </div> | |||
| <div style="float:left;width:170px"> | |||
| ] | |||
| <center>''Circular''</center> | |||
| </div> | |||
| <div style="float:left;width:170px"> | |||
| ] | |||
| <center>''Elliptical''</center> | |||
| </div> | |||
| <br style="clear:both"> | |||
| In the leftmost figure above, the x and y components are in phase. In this case the ratio of the strengths of the two components is constant, so the direction of the electric vector (the vector sum of these two components) is constant. Since the tip of the vector traces out a single line in the plane, this special case is called ]. The direction of this line depends on the relative amplitudes of the two components.<ref name=light /> | |||
| In the middle figure, the two orthogonal components have exactly the same amplitude and are exactly ninety degrees out of phase. In this case one component is zero when the other component is at maximum or minimum amplitude. There are two possible phase relationships that satisfy this requirement: the ''x'' component can be ninety degrees ahead of the ''y'' component or it can be ninety degrees behind the ''y'' component. In this special case the electric vector traces out a circle in the plane, so this special case is called ]. The direction the field rotates in, depends on which of the two phase relationships exists. These cases are called ''right-hand circular polarization'' and ''left-hand circular polarization'', depending on which way the electric vector rotates.<ref name=hecht /> | |||
| In all other cases, where the two components are not in phase and either do not have the same amplitude and/or are not ninety degrees out of phase, the polarization is called ] because the electric vector traces out an ] in the plane (the ''polarization ellipse''). This is shown in the above figure on the right. Detailed mathematics of polarization is done using ] and is characterized by the ].<ref name=hecht /> | |||
| Media that have different indexes of refraction for different polarization modes are called '']''.<ref name=light /> Well known manifestations of this effect appear in optical ]s/retarders (linear modes) and in ]/] (circular modes).<ref name=hecht /> If the path length in the birefringent medium is sufficient, plane waves will exit the material with a significantly different propagation direction, due to ]. For example, this is the case with macroscopic ]s of ], which present the viewer with two offset, orthogonally polarized images of whatever is viewed through them. It was this effect that provided the first discovery of polarization, by ] in 1669. In addition, the phase shift, and thus the change in polarization state, is usually frequency dependent, which, in combination with ], often gives rise to bright colors and rainbow-like effects. In ], this property, known as ], is frequently exploited using polarization ]s, for the purpose of identifying minerals. Additionally, many plastics that are not normally birefringent will become so when subject to ], which is a phenomenon that is the basis of ].<ref name=light /> | |||
| ] | |||
| Media that reduce the amplitude of certain polarization modes are called '']''. with devices that block nearly all of the radiation in one mode known as ''polarizing filters'' or simply "]s". Malus' law, which is named after ], says that when a perfect polarizer is placed in a linear polarized beam of light, the intensity, ''I'', of the light that passes through is given by | |||
| :<math> I = I_0 \cos^2 \theta_i \quad ,</math> | |||
| where | |||
| :''I''<sub>0</sub> is the initial intensity, | |||
| :and ''θ<sub>i</sub>'' is the angle between the light's initial polarization direction and the axis of the polarizer.<ref name=light /> | |||
| A beam of unpolarized light can be thought of as containing a uniform mixture of linear polarizations at all possible angles. Since the average value of <math>\cos^2 \theta</math> is 1/2, the transmission coefficient becomes | |||
| :<math> \frac {I}{I_0} = \frac {1}{2}\quad .</math> | |||
| In practice, some light is lost in the polarizer and the actual transmission of unpolarized light will be somewhat lower than this, around 38% for Polaroid-type polarizers but considerably higher (>49.9%) for some birefringent prism types.<ref name=hecht /> | |||
| In addition to birefringence and dichroism in extended media, polarization effects can also occur at (reflective) interface between two materials of different ]. These effects are treated by the ]. Part of the wave is transmitted and part is reflected, with the ratio depending on angle of incidence and the angle of refraction. In this way, physical optics recovers ].<ref name=hecht /> | |||
| ] on the sky in a photograph. The picture on the right uses the filter optimally adjusted to eliminate certain polarizations of the scattered blue light from the sky.]] | |||
| In nature, ] is often produced by a large number of individual sources, producing waves independently of each other. This type of light is described as '']''. In general there is no single frequency but rather a ] of different frequencies present, and even if filtered to an arbitrarily narrow frequency range, there may not be a consistent state of polarization. However, this does not mean that polarization is only a feature of coherent radiation. Incoherent radiation may show ] between the components of the electric field, which can be interpreted as ''partial polarization''. In general it is possible to describe an observed wave field as the sum of a completely incoherent part (no correlations) and a completely polarized part. One may then describe the light in terms of the ], and the parameters of the polarization ellipse.<ref name=hecht /> | |||
| Light reflected by shiny transparent materials is partly or fully polarized, except when the light is ] (perpendicular) to the surface. It was through this effect that polarization was first discovered in 1808 by the mathematician ]. Polarization by scattering is observed as light passes through the ]. The ] light produces the brightness and color in clear ]. This partial polarization of scattered light can be used to darken the sky in ], increasing the contrast. Optical polarization is principally of importance in ] due to ] and "optical rotation" (]) exhibited by ] (]) ].<ref name=hecht /> | |||
| == Modern optics == | == Modern optics == | ||
| {{main|Optical physics|optical engineering}} | |||
| ''Modern optics'' encompasses the areas of optical science and engineering that became popular in the 20th century. These areas of optical science typically relate to the electromagnetic or quantum properties of light but do include other topics. | |||
| '' |
''Modern optics'' encompasses the areas of optical science and engineering that became popular in the 20th century. These areas of optical science typically relate to the electromagnetic or quantum properties of light but do include other topics. A major subfield of modern optics, ], deals with specifically quantum mechanical properties of light. Quantum optics is not just theoretical; some modern devices have principles of operation that depend on quantum mechanics. For example, ] use ] to amplify light. Light detectors, such as ]s and ]s, respond to individual photons. Electronic ]s, such as ], exhibit ] corresponding to the statistics of individual photon events. ]s and ]s also cannot be understood without quantum mechanics. In the study of these devices, quantum optics often overlaps with ].<ref>D. F. Walls and G. J. Milburn ''Quantum Optics'' (Springer 1994)</ref> | ||
| Specialty areas of optics research include the study of how light interacts with specific materials as in ] and ]s. Other research focus on the phenomenology of electromagnetic waves as in ], ], ], and ]. Additionally, ]s have taken an interest in ], ], and ] as a possible components of the "next generation" of computers.<ref>''Optical Computer Architectures: The Application of Optical Concepts to Next Generation Computers'', ''Optical Computer Architectures: The Application of Optical Concepts to Next Generation Computers'' book by Alastair D. McAulay (1999)</ref> | |||
| === Topics related to modern optics === | |||
| {{Col-begin}} | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ]s | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ]s | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] (]s) | |||
| * ] | |||
| {{Col-end}} | |||
| Today, the pure science of optics is called optical science or ] to distinguish it from applied optical sciences, which are referred to as ]. Prominent subfields of optical engineering include ], ], and ] with practical applications like ], ], and ]. Some of these fields overlap, with nebulous boundaries between the subjects terms that mean slightly different things in different parts of the world and in different areas of industry.<ref>{{cite web|title=SPIE society|url=http://spie.org/}}</ref> A professional community of researchers in ] has developed in the last several decades due to advances in ].<ref>{{cite book|title=The principles of nonlinear optics|author=Shen, Y. R.|publisher=New York, Wiley-Interscience|date=1984}} | |||
| == Other optical fields == | |||
| </ref> | |||
| ===Lasers=== | |||
| {{Col-begin}} | |||
| ]).]] | |||
| {{Col-break|width=33%}} | |||
| {{main|Laser}} | |||
| * ] | |||
| * ] | |||
| A laser is a device that emits ] (]) through a process called '']''. The term ''laser'' is an ] for ''Light Amplification by Stimulated Emission of Radiation''.<ref>{{cite web|accessdate=2008-05-15|url=http://dictionary.reference.com/browse/laser|title=laser |publisher=] }}</ref> Laser light is usually spatially ], which means that the light either is emitted in a narrow, ], or can be converted into one with the help of optical components such as ]es. Because the ] equivalent of the laser, the '']'', was developed first, devices that emit microwave and ] frequencies are usually called ''masers''.<ref name="autogenerated1"></ref> | |||
| * ] | |||
| * ] | |||
| The first working laser was demonstrated on 16 May 1960 by ] at ].<ref>{{cite web|accessdate=2008-05-15|url=http://www.press.uchicago.edu/Misc/Chicago/284158_townes.html|title=The first laser |publisher=]|author=] }}</ref> When first invented, they were called "a solution looking for a problem".<ref>{{cite book|title=A Century of Nature: Twenty-One Discoveries that Changed Science and the World|author= Charles H. Townes |authorlink=Charles Hard Townes|chapter=The first laser|chapterurl=http://www.press.uchicago.edu/Misc/Chicago/284158_townes.html|editor= Laura Garwin and Tim Lincoln|publisher=University of Chicago Press|year=2003|pages=107–12|isbn=0-226-28413-1|accessdate=2008-02-02}}</ref> Since then, lasers have become a multi-billion dollar industry, finding utility in thousands of highly varied applications. | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| The first application of lasers visible in the daily lives of the general population was the supermarket ] scanner, introduced in 1974.<ref name="denso-wave, handheld illustrations" >{{cite web | |||
| * ] | |||
| |title=Handheld barcode scanner technologies, illustrated | |||
| * ] | |||
| |url=http://www.denso-wave.com/en/adcd/fundamental/barcode/scanner.html | |||
| * ] | |||
| }}</ref> The ] player, introduced in 1978, was the first successful consumer product to include a laser, but the ] player was the first laser-equipped device to become truly common in consumers' homes, beginning in 1982.<ref name=BBC6950933>{{cite web | |||
| {{Col-break|width=33%}} | |||
| |url=http://news.bbc.co.uk/2/hi/technology/6950933.stm | |||
| * ] | |||
| |title=How the CD was developed | |||
| * ] | |||
| |author= | |||
| * ] | |||
| |publisher=BBC News | |||
| {{Col-end}} | |||
| |date=2007-08-17 | |||
| |accessdate=2007-08-17 | |||
| }}</ref> These ] devices use a ] less than a millimeter wide to scan the surface of the disc for data retrieval. ] relies on lasers to transmit large amounts of information at speed of light. Other common applications of lasers include ] and ]s. Lasers are used in medicine in areas such as ], ], and ] and in military applications such as ], ], and ]. Lasers are also used in ], ]s, ], and ].<ref>Wilson, J. & Hawkes, J.F.B. (1987). ''Lasers: Principles and Applications'', Prentice Hall International Series in Optoelectronics, ]. ISBN 0-13-523697-5</ref> | |||
| == Everyday optics == | == Everyday optics == | ||
| Optics is part of everyday life. ]s and ]s are examples of optical phenomena. Many people benefit from ] or ], and optics are |
Optics is part of everyday life. ]s and ]s are examples of optical phenomena. Many people benefit from ] or ], and optics are integral to the functioning of many consumer goods including ]. ] are as old as spoken languages and the ubiquity of ]s in biology indicate the central role optics plays as the science of one of the ]. | ||
| == |
===Human eye=== | ||
| ] 6:] 8:] 10:] 22:] 26:] 30:]]] | |||
| {{Col-begin}} | |||
| {{main|human eye|Photometry (optics)}} | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| * ] treatment | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| * ''Optics'', a book by ] | |||
| {{Col-break|width=33%}} | |||
| {{portal|Physics}} | |||
| {{Col-end}} | |||
| The optics of the human eye function when light rays pass through the eye's outer transparent membrane, the ], through the ] aperture, and are focused by the ] on an array of ]s. These cells collectively make up the ] and completely cover the back of the eye with the exception of the location where the ] exits, a fact that results in a ]. The two types of photoreceptor cells, rods and cones, are sensitive to different aspects of light.<ref name=eyeoptics>{{cite book|author=David Atchison and George Smith|title=Optics of the Human Eye|date=Feb, 2000|isbn=0-7506-3775-7|publisher=Elsevier}}</ref> | |||
| === Societies === | |||
| Rod cells are most sensitive to the intensity of the light in a wide frequency range, thus are responsible for ]. Rod cells are not present on the ], the area of the retina responsible for central vision, and are not as responsive as cone cells to spatial and temporal changes in light. There are, however, twenty times more rod cells than cone cells in the retina because the rod cells are present across a wider area. Because of their wider distribution, rods are responsible for ].<ref name="Kandel">{{cite book |last= Kandel |first= E. R. |coauthors= Schwartz, J.H.; Jessell, T.M. |editor= |others= |title= Principles of Neural Science |origdate= |origyear= |origmonth= |url= |format= |accessdate= |edition= 4th |series= |date= |year= 2000 |month= |publisher= McGraw-Hill |location= New York |isbn= 0-8385-7701-6 | oclc= |doi= |id= |pages= 507-513 |chapter= |chapterurl= |quote= }}</ref> | |||
| {{Col-begin}} | |||
| {{Col-break|width=50%}} | |||
| * ] | |||
| * ] | |||
| {{Col-break|width=50%}} | |||
| * ] | |||
| * ] | |||
| {{Col-end}} | |||
| In contrast, cone cells are less sensitive to the overall intensity of light, but come in three varieties that are sensitive to different frequency-ranges and thus are used in the perception of ] and ]. Cone cells are highly concentrated in the fovea and have a high visual acuity meaning that they are better at spatial resolution than rod cells. Since cone cells are not as sensitive to dim light as rod cells, most ] is limited to rod cells. Likewise, since cone cells are in the fovea, central vision (including the vision needed to do most reading, fine detail work such as sewing, or careful examination of objects) is done by cone cells.<ref name="Kandel" /> | |||
| === Wikibooks modules === | |||
| Images are focused on the fovea of the human eye by a ] whose focus can be adjusted by the ]s in a process known as ]. The range of locations where it is possible for the eye to focus images of objects is between a ] and a ] that can be measured by seeing the range of distances from the eye where the person is able to focus and image of an object. For normal vision, the far point is located at infinity while the near point's location depends on how much the muscles can increase the curvature of the lens. ]s, ]s, and ]s usually consider an appropriate near point to be closer than normal reading distance (approximately 25 cm).<ref name=eyeoptics /> | |||
| {{Col-begin}} | |||
| {{Col-break|width=33%}} | |||
| A number of defects in vision happen as a result of optics. As people age, the lens becomes less flexible and the near point recedes from the eye, a condition known as ]. Similarly, people suffering from ] cannot decrease the focal length of their lens enough to allow for nearby objects to be imaged on their retina. Conversely, people who cannot increase the focal length of their lens enough to allow for distant objects to be imaged on the retina suffer from ] and have a far point that is considerably closer than infinity. A condition known as ] results when the cornea is not spherical but instead is more curved in one direction. This causes horizontally extended objects to be focused on different parts of the retina than vertically extended objects, and results in distorted images.<ref name=eyeoptics /> | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| All of these conditions can be corrected using ]es. For presbyopia and hyperopia, a ] provides the extra curvature necessary to bring the near point closer to the eye while for myopia a ] provides the curvature necessary to sent the far point to infinity. Astigmatism is corrected with a ] lens that curves more strongly one direction than another, compensating for the non-uniformity of the cornea.<ref name="Meister_lensdesign">{{cite web |url=http://www.opticampus.com/cecourse.php?url=lens_design/&OPTICAMP=f1e4252df70c63961503c46d0c8d8b60|title=Ophthalmic Lens Design |first=Darryl |last=Meister |work=OptiCampus.com |accessdate=November 12, 2008}}</ref> | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| Corrective lenses are measured in ]s which is the ] of the focal length a positive focal length corresponding to a converging lens and a negative focal length corresponding to a diverging lens. For lenses that correct for astigmatism as well, three numbers are given: one for the spherical power, one for the cylindrical power, and one for the angle of orientation of the astigmatism.<ref name="Meister_lensdesign" /> | |||
| {{Col-end}} | |||
| ===Visual effects=== | |||
| {{main|optical illusions|Perspective (graphical)}} | |||
| ] | |||
| Optical illusions (also called visual illusions) are characterized by ] images that differ from objective reality. The information gathered by the eye is processed in the brain to give a ] that differs from the object being imaged. There are three main types of such illusions: literal optical illusions that create images that are different from the objects that make them, physiological ones that are the effects on the eyes and brain of excessive stimulation of a specific type (brightness, tilt, color, movement), and ] illusions where the eye and brain make unconscious inferences.<ref name="Bryner">'''', Jeanna Bryner, Senior Writer, LiveScience.com 6/2/08.</ref> | |||
| Cognitive illusions that relate to optics include those which rely upon psychological assumptions made due to the conditions of optics. For example, the ], ], ], ], ], ], and ]s all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a ] at infinity in two-dimensionally rendered ].<ref> at </ref> This is also responsible for the famous ] where the moon, despite having essentially the same angular size, appears much larger near the ] than it does at ].<ref>, Don McCready, University of Wisconsin-Whitewater</ref> | |||
| Another type of optical illusion exploits broken patterns to trick the mind into perceiving symmetries or asymmetries that are not present. Examples include the ], ], ], ], and ]s. Related, but not strictly illusions, are patterns that occur due to the superimposition of periodic structures. For example ] tissues with a grid structure, produce shapes known as ]s while the superimposition of periodic transparent patterns comprising parallel opaque lines or curves produces ] patterns.<ref>{{cite book | |||
| | title = Energy Minimization Methods in Computer Vision and Pattern Recognition | |||
| | author = Anil K. Jain, Mário Figueiredo, and Josiane Zerubia (editors) | |||
| | publisher = Springer | |||
| | year = 2001 | |||
| | url = http://books.google.com/books?visbn=3540425233&id=yb8otde21fcC&pg=RA1-PA198&lpg=RA1-PA198&ots=h6DOCc7wXo&dq=%22moire+pattern%22+nonlinear&sig=ayuTVZCBaBOnV-nI5hm6286RP_o | |||
| }}</ref> | |||
| ===Photography=== | |||
| {{main|Science of photography}} | |||
| ] | |||
| ] | |||
| The optics of ] involves both ] and the medium in which the electromagnetic radiation is recorded, whether it be a ], ], or ]. Photographers must consider the ] of the camera and the shot which is summarized by the relation | |||
| :Exposure ∝ ApertureArea × ExposureTime × SceneLuminance<ref> | |||
| {{cite book | |||
| | title = Investigations on the Theory of the Photographic Process | |||
| | author = Samuel Edward Sheppard and Charles Edward Kenneth Mees | |||
| | publisher = Longmans, Green and Co | |||
| | year = 1907 | |||
| | page = 214 | |||
| | url = http://books.google.com/books?id=luNIAAAAIAAJ&pg=PA214&dq=Abney+Schwarzschild+reciprocity+failure&lr=&as_brr=3&as_pt=ALLTYPES&ei=5YCnSayOKYWekwSEr7GiBA | |||
| }}</ref> | |||
| An example of the use of the law of reciprocity is the ] which gives a rough estimate for the settings needed to estimate the proper ] in daylight.<ref>{{cite book | title = Mastering Black-and-White Photography | author = Bernhard J. Suess | publisher = Allworth Communications | year = 2003 | isbn = 1581153066 | url = http://books.google.com/books?id=7LaRPNINH_YC&pg=PT112&dq=%22sunny+16+rule%22&lr=&as_brr=3&ei=6hkZSYPIOoHYtgPMnbAY }}</ref> | |||
| A camera's aperture is measured by a unitless number called the ]s, {{f/}}#, often notated as <math>N</math>, and given by | |||
| :<math>f/\# = N = \frac fD \ </math> | |||
| where <math>f</math> is the ], and <math>D</math> is the diameter of the entrance pupil. By convention, "{{f/}}#" is treated as a single symbol, and specific values of {{f/}}# are written by replacing the ] with the value. The two ways to increase the f-stop are to either decrease the diameter of the entrance pupil or change to a longer focal length (in the case of a ], this can be done by simply adjusting the lens). Higher f-numbers also have a larger ] due to the lens approaching the limit of a ] which is able to focus all images perfectly, regardless of distance, but requires very long exposure times.<ref>{{cite book | title = Basic Photography | author = Michael John Langford | isbn = 0240515927 | year = 2000 | publisher = Focal Press}}</ref> | |||
| When selecting the lens to use, photographers generally consider the field of view that the lens will provide given the specifications of their camera. For a given film or sensor size, specified by the length of the diagonal across the image, a lens may be classified as | |||
| *]: angle of view of the diagonal about 50° and a focal length approximately equal to the diagonal produces this angle.<ref>{{cite book | title = View Camera Technique | author = Leslie D. Stroebel | publisher = Focal Press | year = 1999 | ibsn = 0240803450 | url = http://books.google.com/books?id=71zxDuunAvMC&pg=PA136&dq=appear-normal+focal-length-lens+print-size+diagonal+viewer+distance&lr=&as_brr=3&ei=x8L3R6mMJI-KswPRspyFCg&sig=X65o2ElkUmnoebKyKOIZR7Z0y1I }}</ref> <!-- It's generally accepted that 50mm is a bit longer than "normal" for 35mm film; I've based this on 75mm with 6×4cm. Maybe the angle of width, rather than diagonal, is better? --> | |||
| * ]: angle of view narrower than 25° and focal length longer than normal. These lenses are used for ]s, e.g., for images of the same size as the object. They usually feature a flat field as well, which means that the subject plane is exactly parallel with the film plane.<ref> — Guide to macro photography</ref> | |||
| *]: angle of view wider than 60° and focal length shorter than normal.<ref>{{cite book|title=Using the View Camera|author=Steve Simmons|edition=2, revised, illustrated|publisher=Amphoto Books|date=1992|isbn=0817463534|page=35}}</ref> | |||
| *] or long-focus lens: angle of view narrower and focal length longer than normal. A distinction is sometimes made between a long-focus lens and a true telephoto lens: the telephoto lens uses a ''telephoto group'' to be physically shorter than its focal length.<ref>{{cite book | url = http://books.google.com/books?vid=ISBN0312313675&id=zqkdNwRxSooC&pg=PA109&lpg=PA109&ots=oxbAda_x5B | title = The New York Times Guide to Essential Knowledge | author = New York Times Staff | isbn = 9780312313678 | year = 2004 | publisher = Macmillan }}</ref> | |||
| The absolute value for the exposure time required depends on how ] to light the medium being used is (measured by the ], or, for digital media, by the ]).<ref>{{cite book | title = Principles of Radiographic Imaging: An Art and a Science | author = Richard R. Carlton, Arlene McKenna Adler | publisher = Thomson Delmar Learning | year = 2000 | ibsn = 0766813002 | url = http://books.google.com/books?id=oA-eBHsapX8C&pg=PA318&dq=h%26d-curve+density&lr=&as_brr=3&ei=to3gR5GCLI6eswOs98kV&sig=s_vE4f5PMysrrCtgM7_HJrsRu_Y }}</ref> Early photography used media that had very low light sensitivity, and so exposure times had to be long even for very bright shots. As technology has improved, so has the sensitivity through film cameras and digital cameras. See ] for more on this subject.<ref name="crawford">{{cite book|last=Crawford|first=William|title=The Keepers of Light: A History and Working Guide to Early Photographic Processes|year=1979|publisher=Morgan & Morgan|location=]|isbn=0871001586|page=20}}</ref> | |||
| Other results from physical and geometrical optics apply to camera optics. For example, the maximum resolution capabilities of a particular camera set-up is determined by the ] associated with the pupil size and given, roughly, by the ].<ref>John M. Cowley (1975) ''Diffraction physics'' (North-Holland, Amsterdam) ISBN 0 444 10791 6</ref> | |||
| ===Atmospheric optics=== | |||
| {{main|:Category:Atmospheric optical phenomena}} | |||
| ].]] | |||
| The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue color of the sky is a direct result of ] which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a ] or ]. Additional particulate matter in the sky can scatter different colors at different angles creating colorful glowing skies at dusk and dawn. Scattering off of ice crystals and other particles in the atmosphere are responsible for ], ]s, ], ], and ]s. The variation in these kinds of phenomena are due to different particle sizes and geometries.<ref name=meteorology>{{cite book | |||
| | last = Ahrens | |||
| | first = C. Donald | |||
| | year = 1994 | |||
| | title = Meteorology Today: an introduction to weather, climate, and the environment | |||
| | edition = 5th | |||
| | pages = 88–89 | |||
| | publisher = West Publishing Company | |||
| | location = St. Paul MN | |||
| }}</ref> | |||
| ]s are another sort of optical phenomena due to variations in the ]. Other dramatic optical phenomena associated with this include the ] where the sun appears to rise earlier than predicted with a distorted shape. A spectacular form of refraction occurs with a ] called the ] where objects on the horizon or even beyond the horizon, such as islands, cliffs, ships or icebergs, appear elongated and elevated, like "fairy tale castles".<ref name="An Introduction to Mirages"> by Andy Young</ref> | |||
| ]s are the result of a combination of optical effects: ] and ] of light in raindrops. A single reflection off the back of an array of raindrops produces a coherent rainbow with an angular size on the sky that ranges from 40 to 42 degrees with red on the outside. Double rainbows are produced by two internal reflections with angular size of 50.5 to 54 degrees with violet on the outside. Because rainbows must be seen with the sun 180 degrees away from the center of the rainbow, rainbows are more prominent the closer the sun is to the horizon.<ref name=light /> | |||
| == References == | == References == | ||
| {{Refbegin}} | {{Refbegin}} | ||
| <references/> | <references/> | ||
| === Textbooks === | |||
| * {{cite book | author=Born, Max;Wolf, Emil |title = Principles of Optics (7th ed.)|publisher=Pergamon Press, 1999}} | * {{cite book | author=Born, Max;Wolf, Emil |title = Principles of Optics (7th ed.)|publisher=Pergamon Press, 1999}} | ||
| * {{cite book | author=Hecht, Eugene | title=Optics (4th ed.) | publisher=Pearson Education | year=2001 | isbn=0-8053-8566-5}} | * {{cite book | author=Hecht, Eugene | title=Optics (4th ed.) | publisher=Pearson Education | year=2001 | isbn=0-8053-8566-5}} | ||
| Line 172: | Line 430: | ||
| * {{cite book | author=Lipson, Stephen G. | title=Optical Physics (3rd ed.) | publisher=Cambridge University Press| year=1995 | isbn=0-5214-3631-1}} | * {{cite book | author=Lipson, Stephen G. | title=Optical Physics (3rd ed.) | publisher=Cambridge University Press| year=1995 | isbn=0-5214-3631-1}} | ||
| {{Refend}} | {{Refend}} | ||
| == See also == | |||
| {{Col-begin}} | |||
| {{Col-break|width=33%}} | |||
| * ] | |||
| * ] | |||
| {{Col-break|width=33%}} | |||
| * '']'', a book by ] | |||
| * ''Optics'', a book by ] | |||
| {{Col-break|width=33%}} | |||
| {{portal|Physics}} | |||
| {{Col-end}} | |||
| == External links == | == External links == | ||
| Line 181: | Line 451: | ||
| * — Optics library and community | * — Optics library and community | ||
| === |
==== Wikibooks modules ==== | ||
| * | |||
| {{Col-begin}} | |||
| * | |||
| {{Col-break|width=33%}} | |||
| * | |||
| * ] | |||
| * | |||
| {{Col-break|width=33%}} | |||
| * | |||
| * ] | |||
| * The Internet Portal of the Dutch Photonics Society | |||
| {{Col-break|width=33%}} | |||
| {{Col-end}} | |||
| === Societies === | |||
| {{Col-begin}} | |||
| {{Col-break|width=50%}} | |||
| * ] - | |||
| * ] - | |||
| * ] - | |||
| {{Col-break|width=50%}} | |||
| * ] - | |||
| * ] - | |||
| * ] - | |||
| {{Col-end}} | |||
| ===Periodicals=== | ===Periodicals=== | ||
| Line 199: | Line 484: | ||
| {{physics-footer}} | {{physics-footer}} | ||
| {{Glass science}} | {{Glass science}} | ||
| ] | |||
| ] | |||
| ] | ] | ||
Revision as of 15:07, 6 April 2009
"Optical" redirects here. For the musical artist, see Optical (artist). For the book by Sir Isaac Newton, see Opticks.Optics is the study of the behavior and properties of light, including its interactions with matter and its detection by instruments. The word optics comes from the ancient Greek word Template:Polytonic, meaning appearance or look.
Optics usually describes the behavior of visible light and the behavior of infrared and ultraviolet light, which are similar to visible light but are not detectable by the naked human eye. Other phenomena such as X-rays, microwaves, and radio waves can be described with optical principles because all of these, along with visible light, are types of electromagnetic waves. During the nineteenth century the physicist James Clerk Maxwell discovered that light is a type of electromagnetic radiation; since that time optics has largely been regarded as a sub-field of electromagnetism within theoretical physics.
Classical electromagnetism can be used to describe most everyday optical phenomena. It is usually simpler to use one of the two broad simplifying assumptions for describing light: to treat light as a ray or as a wave. Geometrical optics, developed in the 16th and 17th century, treats light as a collection of rays that travel in straight lines unless they are bent through refraction. Physical optics was developed in the 19th century and accounts for the wave-like nature of light, which is needed in particular to explain interference and diffraction.
Together, geometrical and physical optics encompass classical optics, a system of models capable of describing and predicting many optical phenomena. However, in certain situations, more modern approaches must be used for accurate predictions and explanations. In particular, observations that light behaves both as a particle and as a wave were first correctly explained in the early twentieth century when quantum mechanics replaced classical electromagnetism. Quantum optics deals with the best model of light scientists have developed to date: the photon.
Optical science is relevant to and studied in many related disciplines including electrical engineering, photography, psychology, and medicine (particularly ophthalmology and optometry). Practical applications of optics are found in a variety of technologies and everyday objects, including mirrors, lenses, telescopes, microscopes, lasers, and fiber optics.
History

Optics began with the development of lenses by the ancient Egyptians and Mesopotamians, followed by theories on light and vision developed by ancient Greek and Indian philosophers, and the development of geometrical optics in the Greco-Roman world. The earliest known lenses were made from polished crystal, often quartz, and have been dated as early as 700 BC for Assyrian lenses such as the Layard/Nimrud lens. The ancient Romans and Greeks filled glass spheres with water to make lenses.
Al-Kindi (c. 801–873) was one of the earliest important writers on optics in the Islamic world. In a work known in the west as De radiis stellarum, al-Kindi first articulated emission theory, something not accepted in Europe for another 800 years. This theory of the active power of rays had an influence on later Western scholars such as as Robert Grosseteste and Roger Bacon. In 984, the Persian mathematician, Ibn Sahl wrote a treatise "On Burning Mirrors and Lenses", correctly describing a law of refraction mathematically equivalent to Snell's law. He used his law of refraction to compute the shapes of lenses and mirrors that focus light at a single point on the axis. In the early eleventh century, Ibn al-Haytham wrote his Book of Optics, which extensively documented the then-current Islamic understanding of optics; it included the first descriptions of the optical phenomena associated with pinholes and concave lenses, having great influence in the later development of the modern telescope.
In the thirteenth century, Roger Bacon, inspired by Ibn al-Haytham, used parts of glass spheres as magnifying glasses and discovered that light reflects from objects rather than being released from them. In Italy, around 1284, Salvino D'Armate invented the first wearable eye glasses. The first rudimentary telescopes were developed independently in the 1570s and 1580s by Leonard Digges, Taqi al-Din and Giambattista della Porta.
The earliest known working telescopes were refracting telescopes, a type which rely entirely on lenses for magnification. Their development in the Netherlands in 1608 was by three individuals: Hans Lippershey and Zacharias Janssen, who were spectacle makers in Middelburg, and Jacob Metius of Alkmaar. In Italy, Galileo greatly improved upon these designs the following year. Niccolò Zucchi constructed the first reflecting telescope in 1616, which incorporated a mirror to improve magnification. In 1668, Isaac Newton designed an improved reflecting telescope that bears his name, the Newtonian reflector.
The first microscope was made around 1595 in Middelburg, Holland. Three different eyeglass makers have been given credit for the invention: Hans Lippershey (who also developed the first real telescope); Hans Janssen; and his son, Zacharias. The coining of the name "microscope" has been credited to Giovanni Faber, who gave that name to Galileo's compound microscope in 1625.
Optical theory progressed in the mid-seventeenth century with treatises written by Rene Descartes, which explained a variety of optical phenomena including reflection and refraction by assuming that light was emitted by objects which produced it. This differed substantively from ancient Greek notions that light emanated from the eye. In the late 1660s and early 1670s, Newton expanded Descartes' ideas into a corpuscle theory of light, famously showing that white light, instead of being a unique color, was a really composite of different colors that can be separated into a spectrum with a prism. In 1690, Christian Huygens proposed a wave theory for light based on suggestions that had been made by Robert Hooke in 1664. Hooke himself publicly criticized Newton's theories of light; the feud between the two lasted until Hooke's death. In 1704, Newton published Opticks and, at the time, partly because of his success in other areas of physics, was generally considered to be the victor in the debate over the nature of light.
Newtonian optics and emission theory was generally accepted as correct until the early nineteenth century when Thomas Young and Augustin-Jean Fresnel conducted experiments in the interference of light that firmly established light's wave-nature. Young's famous double slit experiment showed that light followed the law of superposition, something normal particles do not follow. This experiment lead to a theory of diffraction for light and opened an entire theory of physical optics, This was the optical theory that was successfully unified with electromagnetic theory by James Clerk Maxwell in the 1860s.
The next development in optical theory came in 1899 when Max Planck correctly modeled blackbody radiation by assuming that the exchange of energy between light and matter only occurred in discrete amounts he called quanta. In 1905, Albert Einstein published the theory of the photoelectric effect that firmly established the quantization of light itself. In 1913, Niels Bohr showed that atoms could only emit discrete amounts of energy, thus explaining the discrete lines seen in emission and absorption spectra. The understanding of the interaction between light and matter, which followed from these developments, not only formed the basis of quantum optics but also was crucial for the development of quantum mechanics as a whole.
Quantum optics gained practical importance with the invention of the maser in 1953 and the laser in 1960. Following the work of Dirac in quantum field theory, George Sudarshan, Roy J. Glauber, and Leonard Mandel applied quantum theory to the electromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the statistics of light. The ultimate culmination was the theory of quantum electrodynamics, which explains all optics and electromagnetic processes in general as being the result of the exchange of real and virtual photons.
Classical optics

Classical optics works by modeling light as an electromagnetic wave composed of oscillating electric and magnetic fields. These fields generate each other according to Maxwell's equations as the wave propagates through space and oscillates in time.
The frequency of light waves is determined by the period of the oscillations of the emitter. While the frequency of a light wave does not normally change as light transmits through different materials, called optical media, the wavelength of light is affected by the indexes of refraction in different media. Since the speed (v) of any wave is related by the formula
where is the wavelength and is the frequency of the wave, a changing wavelength results in a changing speed of light. This can be characterized with by the index of refraction, a unitless number defined as
where c is the speed of light in a vacuum -- a constant value equal to 299,792,458 metres per second.
The amplitude of the light wave is related to the intensity of the light which is related to the energy stored in the electric and magnetic fields of the light wave.
Before quantum optics became important, optics consisted mainly of the application of classical electromagnetism and its high frequency approximations to light. Classical optics divides into two main branches: geometrical optics and physical optics.
Geometrical optics
Main article: Geometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", that can be used to predict the path of light. A light ray is a a ray that is perpendicular to a wavefronts of a light (therefore collinear with the wave vector). Light rays bend at the interface between two dissimilar media, and may be curved in a medium in which the refractive index changes. Geometrical optics provides rules for propagating these rays through an optical system, which indicates how the actual wavefront will propagate. This is a significant simplification of optics that fails to account for optical effects such as diffraction and polarization. It is a good approximation, however, when the wavelength is very small compared with the size of structures with which the light interacts. Geometric optics can be used to describe the geometrical aspects of imaging, including optical aberrations.
A slightly more rigorous definition of a light ray follows from Fermat's principle which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.
Approximations
Geometric optics is often simplified even further by making the paraxial approximation, or "small angle approximation." The mathematical behavior then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics and paraxial ray tracing, which are used to find basic properties of optical systems, such as approximate image and object positions and magnifications.
The Gaussian beam propagation is an expansion of paraxial optics that provides a more accurate model of coherent radiation like laser beams. While still using the paraxial approximation, this technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics.
Reflections
Main article: reflection
Reflections can be divided into two types: specular reflection and diffuse reflection. In diffuse reflection, the wavefronts do not maintain paraxiality due to imperfections in the reflecting surface. Modeling of diffuse reflection can only be done in a statistical, average sense, generally characterized by an albedo that indicates a certain amount of light intensity is lost during the reflection due to absorption.
Specular reflection, in comparison, occurs when the wavefronts maintain paraxiality due to reflection off of a mirror surface. This allows for production of coherent images that can be associated with an actual (real) or extrapolated (virtual) location in space. An incident ray meets a surface at an angle with respect to normal called the angle of incidence () and reflects off the surface at an angle with respect to normal called the angle of reflection (). The law of reflection states
- .
For flat mirrors, the law of reflection implies that the images of objects are upright and the same distance behind the mirror as the distance that objects are in front of the mirror and the image size is the same as the object size (i.e. the magnification of a flat mirror is unity). The law also implies that mirror images are parity inverted (i.e. left and right are interchanged). Corner reflectors can be used to create reflections that are not parity inverted and also minimize the scattering of the light rays.
Mirrors that have curvature can be modeled by ray-tracing and using the law of reflection at each point of the tangent plane to surface. For parabolic surfaces, the parallel rays incident on the mirror will all converge at a focal point. Other curved surfaces will also exhibit a focal point with aberrations due to the diverging shape causing the focal point to be smeared out in space. The most famous example of this is the so-called spherical aberration. The images of objects seen in a curved mirror follow the mirror equation which relates the object distance () and image distances () to the focal length ():
- .
The magnification of a mirror is defined as the height of the image divided by the height of the object:
- .
The negative sign in this equation is used as a convention. By convention, if the magnification is positive, the image is upright. If the magnification is negative, the image is inverted (upside down). Upright images in mirrors are virtual images while inverted images are real and can be projected onto a screen.
Refractions
Main article: Refraction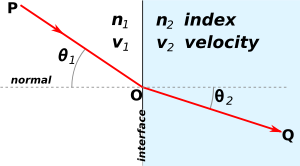
Refraction occurs when light travels through an area of space that has a changing index of refraction. The simplest case of refraction occurs when there is a simple interface between one medium with index of refraction and another medium with index of refraction . In such situations, Snell's Law describes the resulting deflection of the light ray:
where and are the angles between the normal (to the interface) plane and the incident waves respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
where and are the wave velocities through the respective media.
Various consequences of Snell's Law include the fact that for light rays traveling from a material with a high index of refraction to a material with a low index of refraction, it is possible for the interaction with the interface to result in zero transmission. This phenomenon is called total internal reflection and allows for fiber optics technology. Another refraction scenario of note is the situation where the refracted ray and the reflected ray form a right angle. The angle of incidence required for such a scenario is known as Brewster's angle and results in the production of polarized light rays.
Snell's Law can be used to predict the deflection of light rays as they pass through "linear media" as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. Additionally, since different frequencies of light have slightly different indexes of refraction in most materials, refraction can be used to produce dispersion spectra that appear as rainbows. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.
Some media have an index of refraction which changes and, thus, light rays end up curving through the medium rather than traveling in straight lines. This effect is what is responsible for mirages seen on hot days where the changing index of refraction of the air causes the light rays to bend creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Material that has a changing index of refraction is called a gradient-index (GRIN) material and has many useful properties used in modern optical scanning technologies including photocopiers and scanners. The phenomenon is studied in the field of gradient-index optics.
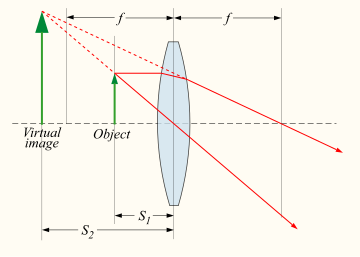
A device which produces converging or diverging light rays due to refraction is known as a lens. Thin lenses produce focal points on either side that can be modeled using the lensmaker's equation. In general, two types of lenses exist: convex lenses which cause parallel light rays to converge and concave lenses which cause parallel light rays to diverge. The detail prediction of how images are produced in these lenses can be made using ray-tracing similar to curved mirrors. Also similar to curved mirrors, thin lenses follow a simple equation that determines the location of the images given a particular focal length () and object distance ():
where is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.
Likewise, the magnification of a lens is given by
where the negative sign is given, by convention, to indicate an upright object for positive values and an inverted object for negative values. Similar to mirrors, upright images produced by single lenses are virtual while inverted images are real.
Lenses suffer from aberrations that distort images and focal points. These are due to both to geometrical imperfections and due to the changing index of refraction for different wavelengths of light (chromatic aberration).
Optical instruments

Single lenses have a variety of applications including photographic lenses, corrective lenses, and magnifying glasses while single mirrors are used in parabolic reflectors and rear-view mirrors. Combining a number of mirrors, prisms, and lenses produces compound optical instruments which have practical uses. For example, a periscope is simply two plane mirrors aligned to allow for viewing around obstructions. The most famous compound optical instruments in science are the microscope and the telescope which were both invented by the Dutch in the late 16th century.
Microscopes were first developed with just two lenses: an objective lens and an eyepiece. The objective lens is essentially a magnifying glass and was designed with a very small focal length while the eyepieces generally has longer focal lengths. This has the effect of producing magnified images of close objects. Generally, an additional source of illumination is used since magnified images are dimmer due to the conservation of energy and the spreading of light rays over a larger surface area. Modern microscopes, known as compound microscopes have many lenses in them (typically four) to optimize the functionality and enhance image stability. A slightly different variety of microscope, the comparison microscope, looks at side-by-side images to produce a stereoscopic binocular view that appears three dimensional when used by humans.
The first telescopes, called refracting telescopes were also developed with a single objective and eyepiece lens. In contrast to the microscope, the objective lens of the telescope was designed with a large focal length to avoid optical aberrations. The objective focuses an image of an object that is essentially at infinity at its focal point which is adjusted to be at the focal point of an eyepiece which is generally of a much smaller focal length. The main goal of a telescope is not necessarily magnification, but rather collection of light which is determined by the physical size of the objective lens. Thus, telescopes are normally indicated by the diameters of their objectives rather than by the magnification which can be changed by switching eyepieces. Because the magnification of a telescope is equal to the focal length of the objective divided by the focal length of the eyepiece, smaller focal-legnth eyepieces cause greater magnification.
Since crafting large lenses is much more difficult than crafting large mirrors, most modern telescopes are reflecting telescopes, that is, telescopes that use a primary mirror rather than an objective lens. The same general optical considerations apply to reflecting telescopes that applied to refracting telescopes, namely, the larger the primary mirror, the more light collected ad the magnification is still equal to the focal length of the primary mirror divided by the focal length of the eyepiece. Professional class telescopes generally do not have eyepieces and instead place an instrument (often a charge-coupled device) at the focal point instead.
Physical optics
Main article: Physical opticsPhysical optics or wave optics builds on Huygens's principle which states that every point on an advancing wavefront is the center of a new disturbance. When combined with the superposition principle, this allows for an explanation of how optical phenomena are manifested when there are multiple sources or obstructions that are spaced at similar size as the wavelength of the light.
Complex models based on physical optics can account for the propagation of any wavefront through an optical system, including the wavelength, amplitude, and phase of the wave. Additionally, all of the results from geometrical optics can be recovered using the techniques of Fourier optics which apply many of the same mathematical and analytical techniques used in acoustic engineering and signal processing. Using numerical modeling on a computer, optical scientists can account for most diffraction, interference, and polarization effects, as well as other complex interference patterns. Physical optics still relies on approximations, however, so this is not a full electromagnetic wave theory model of the propagation of light. Such a full model is much more computationally demanding and is normally only used to solve small-scale problems that require more accurate treatments.
Superposition and interference
Main articles: superposition principle and interferenceThe principle of superposition can be used to predict the precise shape of interacting waveforms through the simple addition of the disturbances. The resulting wave pattern is generally termed "interference" and can result in a variety of outcomes. If two waves of the same wavelength and frequency are in phase, then the wave crests align with other crests and wave troughs align with other troughs. This results in constructive interference and an increase in the amplitude of the wave, which for light is associated with a brightening of the waveform in that location. Alternatively, if the two waves of the same wavelength and frequency are out of phase, then the wave crests will align with wave troughs and vice-versa. This results in destructive interference and a decrease in the amplitude of the wave, which for light is associated with a dimming of the waveform at that location. See below for an illustration of this effect.
| combined waveform |
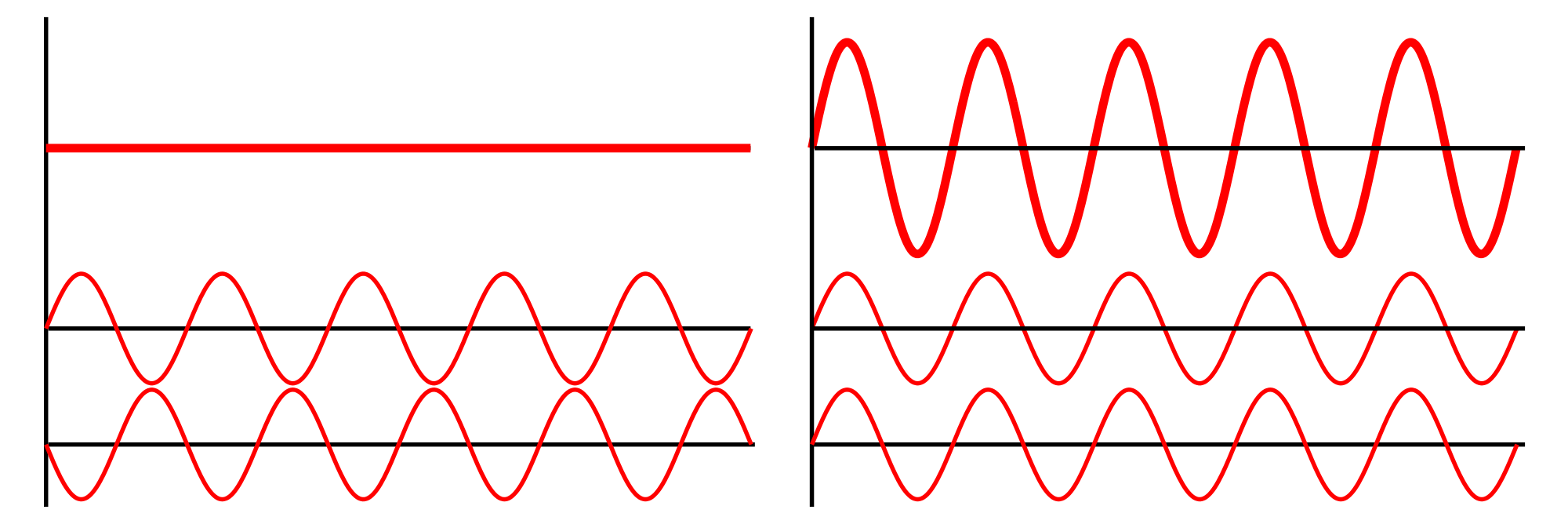
| |
| wave 1 | ||
| wave 2 | ||
| Two waves in phase | Two waves 180° out of phase | |
Since Huygens's principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns. Inteferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famously used interference effects to accurately measure the speed of light.

The appearance of thin-films and coatings is directly affected by interference effects. Nonreflective coatings have an index of refraction less than the material on which they are deposited. Such coatings minimize glare and can eliminate a large amount of unwanted reflection. If the thin film has a thickness that is one fourth the wavelength of incident light, the reflected wave from the top of the film and the reflected wave from the film/material interface will be exactly 180 degrees out-of-phase causing destructive interference. Since this can only be done for one particular wavelength, usually a wavelength associated with yellow-green (nm) where the sun is the brightest is chosen. Alternatively, if the thin-film coating has an index of refraction greater than than the material on which it is deposited, then the reflected wave from the top of the film and the reflected wave from the film/material interface will be in phase when the film has a thickness of one fourth a wavelength. Such optical coatings are used for heat reflectors on astronaut visors and for color separation in color television cameras. This interference effect is also what causes the colorful rainbow patterns seen in oil slicks.
Diffraction and optical resolution
Main articles: diffraction and optical resolution
Diffraction is the process by which light interference is most commonly observed. The effect was first described in 1665 by Francesco Maria Grimaldi who also coined the term diffraction, from the Latin diffringere, 'to break into pieces', referring to light breaking up into different directions. Later that century, Robert Hooke and Isaac Newton also described phenomena now known to be diffraction in Newton's rings while James Gregory recorded his observations of diffraction patterns from bird feathers.
The first physical optics model of diffraction that relied on Huygen's Principle was developed in 1803 by Thomas Young in his accounts of the interference patterns of from two closely spaced slits. Explaining his results by interference of the waves emanating from the two different slits, he deduced that light must propagate as waves. Augustin-Jean Fresnel did more definitive studies and calculations of diffraction, published in 1815 and 1818.
The simplest physical models of diffraction use by equations that describe the angular separation of light and dark fringes due to light of a particular wavelength (). In general, the equation takes the form
where is the separation between two wavefront sources (in the case of Young's experiments, it was two slits), is the angular separation between the central fringe and the th order fringe, where the central maximum is .
This equation is modified slightly to take into account a variety of situations such diffraction through a single gap, diffraction through multiple slits, or diffraction through a diffraction grating that contains a large number of slits at equal spacing. More complicated models of diffraction require working with the mathematics of Fresnel or Fraunhofer diffraction.
X-ray diffraction makes use of the fact that atoms in a crystal have regular spacing at distances that are on the order of one angstrom. To see diffraction patterns, x-rays with similar wavelengths to that spacing are passed through the crystal. Since crystals are three-dimensional objects rather than two dimensional gratings, the associated diffraction pattern varies in two directions according to Bragg reflection with the associated bright spots occurring in unique patterns and being twice the spacing between atoms.
Diffraction effects limit the ability for an optical detector to optically resolve separate light sources. In general, light that is passing through an aperture will experience diffraction and the best images that can be created (so-called diffraction-limited optics) appear as acentral spot with surrounding bright rings, separated by dark nulls; this pattern is known as an Airy pattern, and the central bright lobe as an Airy disk. The size of such a disk is given by
where θ is the angular resolution, λ is the wavelength of light, and D is the diameter of the lens aperture. If the angular separation of the two points is significantly less than the Airy disk angular radius, then the two points cannot be resolved in the image, but if their angular separation is much greater than this, distinct images of the two points are formed and they can therefore be resolved. Rayleigh defined the somewhat arbitrary "Rayleigh criterion" that two points whose angular separation is equal to the Airy disk radius to first null can be considered to be resolved. It can be seen that the greater the diameter of the lens or its aperture, the finer the resolution. Inteferometry, with its ability to mimic extremely large baseline aperatures, allows for the greatest angular resolution possible.
For astronomical imaging, the atmosphere prevents optimal resolution from being achieved in the visible spectrum due to the atmospheric scattering and dispersion which cause stars to twinkle. Astronomers refer to this effect as the quality of astronomical seeing. Techniques known as adaptive optics have been utilized to eliminate the atmospheric disruption of images and achieve results that approach the diffraction limit.
Dispersion and scattering
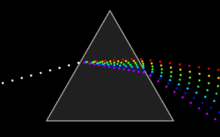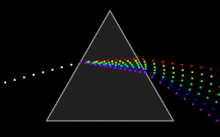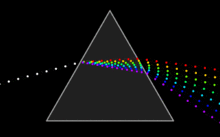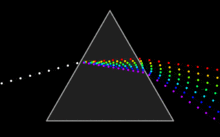
Refractive processes take place in the physical optics limit as a kind of scattering. The simplest type of scattering is Thomson scattering which occurs when electromagnetic waves are deflected by single particles. In the limit of Thompson scattering, light is dispersed independent of the frequency, in contrast to Compton scattering which is frequency-dependent and strictly a quantum mechanical process. In a statistical sense, elastic scattering of light by numerous particles much smaller than the wavelength of the light is a process known as Rayleigh scattering while the similar process for scattering by particles that are similar or larger in wavelength is known as Mie scattering with the Tyndall effect being a commonly observed result. Raman scattering occurs in situations where the frequency changes due to excitation of atoms and molecules and Brillouin scattering occurs when the frequency of light changes due to local changes and movements of a dense material.
Dispersion occurs when different frequencies of light have different phase velocities due to either material differences (material dispersion) or due to the geometry of an optical waveguide (waveguide dispersion). The most commonly observed dispersion observed is due to the fact that for visible light, most transparent materials (e.g. glasses) have:
or alternatively:
that is, refractive index n decreases with increasing wavelength λ. In this case, the medium is said to have normal dispersion. Whereas, if the index increases with increasing wavelength the medium has anomalous dispersion.
At the interface of such a material with air or vacuum (index of ~1), Snell's law predicts that light incident at an angle θ to the normal will be refracted at an angle arcsin( sin (θ) / n) . Thus, blue light, with a higher refractive index, will be bent more strongly than red light, resulting in the well-known rainbow pattern.

Material dispersion is characterized by the Abbe number which relates the refractive index of the material to how it changes as a function of frequency. Waveguide dispersion is dependent on how the propagation constant of the situation changes. Both kinds of dispersion cause changes in the group characteristics of the wave, the features of the wave packet that change with the same frequency as the amplitude of the electromagnetic wave. "Group velocity dispersion" manifests as a spreading-out of the signal "envelope" of the radiation and can be quantified as a group dispersion delay parameter:
where is the group velocity. For a uniform medium, the group velocity is
where n is the index of refraction and c is the speed of light in a vacuum. This gives a simpler form for the dispersion delay parameter:
If D is less than zero, the medium is said to have positive dispersion. If D is greater than zero, the medium has negative dispersion. If a light pulse is propagated through a normally dispersive medium, the result is the higher frequency components slow down more than the lower frequency components. The pulse therefore becomes positively chirped, or up-chirped, increasing in frequency with time. This causes the spectrum coming out of a prism to appear with red light the least refracted and blue/violet light the most refracted. Conversely, if a pulse travels through an anomalously dispersive medium, high frequency components travel faster than the lower ones, and the pulse becomes negatively chirped, or down-chirped, decreasing in frequency with time.
The result of group velocity dispersion, whether negative or positive, is ultimately temporal spreading of the pulse. This makes dispersion management extremely important in optical communications systems based on optical fibers, since if dispersion is too high, a group of pulses representing will spread in time and merge together, making it impossible to extract the signal.
Polarization
Main article: PolarizationPolarization is a general property of waves that describes the orientation of their oscillations. For transverse waves such as many electromagnetic waves, it describes the orientation of the oscillations in the plane perpendicular to the wave's direction of travel. The oscillations may be oriented in a single direction (linear polarization), or the oscillation direction may rotate as the wave travels (circular or elliptical polarization). Circularly polarized waves can rotate rightward or leftward in the direction of travel, and which of those two rotations is present in a wave is called the wave's chirality.
The typical way to consider polarization is to keep track of the orientation of the electric field vector as the electromagnetic wave propagates. The electric field vector of a plane wave may be arbitrarily divided into two perpendicular components labeled x and y (with z indicating the direction of travel). The shape traced out in the x-y plane by the electric field vector is a Lissajous figure that describes the polarization state. The following figures show some examples of the evolution of the electric field vector (blue), with time (the vertical axes), at a particular point in space, along with its x and y components (red/left and green/right), and the path traced by the vector in the plane (purple): The same evolution would occur when looking at the electric field at a particular time while evolving the point in space, along the direction opposite to propagation.
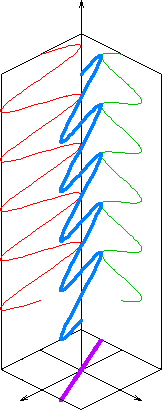


In the leftmost figure above, the x and y components are in phase. In this case the ratio of the strengths of the two components is constant, so the direction of the electric vector (the vector sum of these two components) is constant. Since the tip of the vector traces out a single line in the plane, this special case is called linear polarization. The direction of this line depends on the relative amplitudes of the two components.
In the middle figure, the two orthogonal components have exactly the same amplitude and are exactly ninety degrees out of phase. In this case one component is zero when the other component is at maximum or minimum amplitude. There are two possible phase relationships that satisfy this requirement: the x component can be ninety degrees ahead of the y component or it can be ninety degrees behind the y component. In this special case the electric vector traces out a circle in the plane, so this special case is called circular polarization. The direction the field rotates in, depends on which of the two phase relationships exists. These cases are called right-hand circular polarization and left-hand circular polarization, depending on which way the electric vector rotates.
In all other cases, where the two components are not in phase and either do not have the same amplitude and/or are not ninety degrees out of phase, the polarization is called elliptical polarization because the electric vector traces out an ellipse in the plane (the polarization ellipse). This is shown in the above figure on the right. Detailed mathematics of polarization is done using Jones calculus and is characterized by the Stokes parameters.
Media that have different indexes of refraction for different polarization modes are called birefringent. Well known manifestations of this effect appear in optical wave plates/retarders (linear modes) and in Faraday rotation/optical rotation (circular modes). If the path length in the birefringent medium is sufficient, plane waves will exit the material with a significantly different propagation direction, due to refraction. For example, this is the case with macroscopic crystals of calcite, which present the viewer with two offset, orthogonally polarized images of whatever is viewed through them. It was this effect that provided the first discovery of polarization, by Erasmus Bartholinus in 1669. In addition, the phase shift, and thus the change in polarization state, is usually frequency dependent, which, in combination with dichroism, often gives rise to bright colors and rainbow-like effects. In mineralogy, this property, known as pleochroism, is frequently exploited using polarization microscopes, for the purpose of identifying minerals. Additionally, many plastics that are not normally birefringent will become so when subject to mechanical stress, which is a phenomenon that is the basis of photoelasticity.

In this picture, θ1 - θ0 = θi.
Media that reduce the amplitude of certain polarization modes are called dichroic. with devices that block nearly all of the radiation in one mode known as polarizing filters or simply "polarizers". Malus' law, which is named after Etienne-Louis Malus, says that when a perfect polarizer is placed in a linear polarized beam of light, the intensity, I, of the light that passes through is given by
where
- I0 is the initial intensity,
- and θi is the angle between the light's initial polarization direction and the axis of the polarizer.
A beam of unpolarized light can be thought of as containing a uniform mixture of linear polarizations at all possible angles. Since the average value of is 1/2, the transmission coefficient becomes
In practice, some light is lost in the polarizer and the actual transmission of unpolarized light will be somewhat lower than this, around 38% for Polaroid-type polarizers but considerably higher (>49.9%) for some birefringent prism types.
In addition to birefringence and dichroism in extended media, polarization effects can also occur at (reflective) interface between two materials of different refractive index. These effects are treated by the Fresnel equations. Part of the wave is transmitted and part is reflected, with the ratio depending on angle of incidence and the angle of refraction. In this way, physical optics recovers Brewster's angle.

In nature, electromagnetic radiation is often produced by a large number of individual sources, producing waves independently of each other. This type of light is described as incoherent. In general there is no single frequency but rather a spectrum of different frequencies present, and even if filtered to an arbitrarily narrow frequency range, there may not be a consistent state of polarization. However, this does not mean that polarization is only a feature of coherent radiation. Incoherent radiation may show statistical correlation between the components of the electric field, which can be interpreted as partial polarization. In general it is possible to describe an observed wave field as the sum of a completely incoherent part (no correlations) and a completely polarized part. One may then describe the light in terms of the degree of polarization, and the parameters of the polarization ellipse.
Light reflected by shiny transparent materials is partly or fully polarized, except when the light is normal (perpendicular) to the surface. It was through this effect that polarization was first discovered in 1808 by the mathematician Etienne Louis Malus. Polarization by scattering is observed as light passes through the atmosphere. The scattered light produces the brightness and color in clear skies. This partial polarization of scattered light can be used to darken the sky in photographs, increasing the contrast. Optical polarization is principally of importance in chemistry due to circular dichroism and "optical rotation" (circular birefringence) exhibited by optically active (chiral) molecules.
Modern optics
Main articles: Optical physics and optical engineeringModern optics encompasses the areas of optical science and engineering that became popular in the 20th century. These areas of optical science typically relate to the electromagnetic or quantum properties of light but do include other topics. A major subfield of modern optics, quantum optics, deals with specifically quantum mechanical properties of light. Quantum optics is not just theoretical; some modern devices have principles of operation that depend on quantum mechanics. For example, lasers use stimulated emission of radiation to amplify light. Light detectors, such as photomultipliers and channeltrons, respond to individual photons. Electronic image sensors, such as CCDs, exhibit shot noise corresponding to the statistics of individual photon events. Light-emitting diodes and photovoltaic cells also cannot be understood without quantum mechanics. In the study of these devices, quantum optics often overlaps with quantum electronics.
Specialty areas of optics research include the study of how light interacts with specific materials as in crystal optics and metamaterials. Other research focus on the phenomenology of electromagnetic waves as in singular optics, non-imaging optics, statistical optics, and radiometry. Additionally, computer engineers have taken an interest in integrated optics, machine vision, and photonic computing as a possible components of the "next generation" of computers.
Today, the pure science of optics is called optical science or optical physics to distinguish it from applied optical sciences, which are referred to as optical engineering. Prominent subfields of optical engineering include illumination engineering, photonics, and optoelectronics with practical applications like lens design, fabrication and testing of optical components, and image processing. Some of these fields overlap, with nebulous boundaries between the subjects terms that mean slightly different things in different parts of the world and in different areas of industry. A professional community of researchers in nonlinear optics has developed in the last several decades due to advances in laser technology.
Lasers

A laser is a device that emits light (electromagnetic radiation) through a process called stimulated emission. The term laser is an acronym for Light Amplification by Stimulated Emission of Radiation. Laser light is usually spatially coherent, which means that the light either is emitted in a narrow, low-divergence beam, or can be converted into one with the help of optical components such as lenses. Because the microwave equivalent of the laser, the maser, was developed first, devices that emit microwave and radio frequencies are usually called masers.
The first working laser was demonstrated on 16 May 1960 by Theodore Maiman at Hughes Research Laboratories. When first invented, they were called "a solution looking for a problem". Since then, lasers have become a multi-billion dollar industry, finding utility in thousands of highly varied applications.
The first application of lasers visible in the daily lives of the general population was the supermarket barcode scanner, introduced in 1974. The laserdisc player, introduced in 1978, was the first successful consumer product to include a laser, but the compact disc player was the first laser-equipped device to become truly common in consumers' homes, beginning in 1982. These optical storage devices use a semiconductor laser less than a millimeter wide to scan the surface of the disc for data retrieval. Fiber-optic communication relies on lasers to transmit large amounts of information at speed of light. Other common applications of lasers include laser printers and laser pointers. Lasers are used in medicine in areas such as bloodless surgery, laser eye surgery, and laser capture microdissection and in military applications such as missile defense systems, electro-optical countermeasures (EOCM), and LIDAR. Lasers are also used in holograms, bubblegrams, laser light shows, and laser hair removal.
Everyday optics
Optics is part of everyday life. Rainbows and mirages are examples of optical phenomena. Many people benefit from eyeglasses or contact lenses, and optics are integral to the functioning of many consumer goods including cameras. Languages based on optical signals are as old as spoken languages and the ubiquity of visual systems in biology indicate the central role optics plays as the science of one of the five senses.
Human eye

The optics of the human eye function when light rays pass through the eye's outer transparent membrane, the cornea, through the pupil aperture, and are focused by the lens on an array of photoreceptor cells. These cells collectively make up the retina and completely cover the back of the eye with the exception of the location where the optic nerve exits, a fact that results in a blind spot. The two types of photoreceptor cells, rods and cones, are sensitive to different aspects of light.
Rod cells are most sensitive to the intensity of the light in a wide frequency range, thus are responsible for black-and-white vision. Rod cells are not present on the fovea, the area of the retina responsible for central vision, and are not as responsive as cone cells to spatial and temporal changes in light. There are, however, twenty times more rod cells than cone cells in the retina because the rod cells are present across a wider area. Because of their wider distribution, rods are responsible for peripheral vision.
In contrast, cone cells are less sensitive to the overall intensity of light, but come in three varieties that are sensitive to different frequency-ranges and thus are used in the perception of color and photopic vision. Cone cells are highly concentrated in the fovea and have a high visual acuity meaning that they are better at spatial resolution than rod cells. Since cone cells are not as sensitive to dim light as rod cells, most night vision is limited to rod cells. Likewise, since cone cells are in the fovea, central vision (including the vision needed to do most reading, fine detail work such as sewing, or careful examination of objects) is done by cone cells.
Images are focused on the fovea of the human eye by a lens whose focus can be adjusted by the ciliary muscles in a process known as accommodation. The range of locations where it is possible for the eye to focus images of objects is between a far point and a near point that can be measured by seeing the range of distances from the eye where the person is able to focus and image of an object. For normal vision, the far point is located at infinity while the near point's location depends on how much the muscles can increase the curvature of the lens. Optometrists, opthamologists, and opticians usually consider an appropriate near point to be closer than normal reading distance (approximately 25 cm).
A number of defects in vision happen as a result of optics. As people age, the lens becomes less flexible and the near point recedes from the eye, a condition known as presbyopia. Similarly, people suffering from hyperopia cannot decrease the focal length of their lens enough to allow for nearby objects to be imaged on their retina. Conversely, people who cannot increase the focal length of their lens enough to allow for distant objects to be imaged on the retina suffer from myopia and have a far point that is considerably closer than infinity. A condition known as astigmatism results when the cornea is not spherical but instead is more curved in one direction. This causes horizontally extended objects to be focused on different parts of the retina than vertically extended objects, and results in distorted images.
All of these conditions can be corrected using corrective lenses. For presbyopia and hyperopia, a converging lens provides the extra curvature necessary to bring the near point closer to the eye while for myopia a diverging lens provides the curvature necessary to sent the far point to infinity. Astigmatism is corrected with a cylindrical surface lens that curves more strongly one direction than another, compensating for the non-uniformity of the cornea.
Corrective lenses are measured in diopters which is the reciprocal of the focal length a positive focal length corresponding to a converging lens and a negative focal length corresponding to a diverging lens. For lenses that correct for astigmatism as well, three numbers are given: one for the spherical power, one for the cylindrical power, and one for the angle of orientation of the astigmatism.
Visual effects
Main articles: optical illusions and Perspective (graphical)
Optical illusions (also called visual illusions) are characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a percept that differs from the object being imaged. There are three main types of such illusions: literal optical illusions that create images that are different from the objects that make them, physiological ones that are the effects on the eyes and brain of excessive stimulation of a specific type (brightness, tilt, color, movement), and cognitive illusions where the eye and brain make unconscious inferences.
Cognitive illusions that relate to optics include those which rely upon psychological assumptions made due to the conditions of optics. For example, the Ames room, Hering, Müller-Lyer, Orbison, Ponzo, Sander, and Wundt illusions all rely on the suggestion of the appearance of distance by using converging and diverging lines, in the same way that parallel light rays (or indeed any set of parallel lines) appear to converge at a vanishing point at infinity in two-dimensionally rendered images with artistic perspective. This is also responsible for the famous moon illusion where the moon, despite having essentially the same angular size, appears much larger near the horizon than it does at zenith.
Another type of optical illusion exploits broken patterns to trick the mind into perceiving symmetries or asymmetries that are not present. Examples include the café wall, Ehrenstein, Fraser spiral, Poggendorff, and Zöllner illusions. Related, but not strictly illusions, are patterns that occur due to the superimposition of periodic structures. For example transparent tissues with a grid structure, produce shapes known as moiré patterns while the superimposition of periodic transparent patterns comprising parallel opaque lines or curves produces line moiré patterns.
Photography
Main article: Science of photography

The optics of photography involves both lenses and the medium in which the electromagnetic radiation is recorded, whether it be a plate, film, or charge-coupled device. Photographers must consider the reciprocity of the camera and the shot which is summarized by the relation
- Exposure ∝ ApertureArea × ExposureTime × SceneLuminance
An example of the use of the law of reciprocity is the Sunny 16 rule which gives a rough estimate for the settings needed to estimate the proper exposure in daylight.
A camera's aperture is measured by a unitless number called the f-numbers, f/#, often notated as , and given by
where is the focal length, and is the diameter of the entrance pupil. By convention, "f/#" is treated as a single symbol, and specific values of f/# are written by replacing the number sign with the value. The two ways to increase the f-stop are to either decrease the diameter of the entrance pupil or change to a longer focal length (in the case of a zoom lens, this can be done by simply adjusting the lens). Higher f-numbers also have a larger depth of field due to the lens approaching the limit of a pinhole camera which is able to focus all images perfectly, regardless of distance, but requires very long exposure times.
When selecting the lens to use, photographers generally consider the field of view that the lens will provide given the specifications of their camera. For a given film or sensor size, specified by the length of the diagonal across the image, a lens may be classified as
- Normal lens: angle of view of the diagonal about 50° and a focal length approximately equal to the diagonal produces this angle.
- Macro lens: angle of view narrower than 25° and focal length longer than normal. These lenses are used for close-ups, e.g., for images of the same size as the object. They usually feature a flat field as well, which means that the subject plane is exactly parallel with the film plane.
- Wide-angle lens: angle of view wider than 60° and focal length shorter than normal.
- Telephoto lens or long-focus lens: angle of view narrower and focal length longer than normal. A distinction is sometimes made between a long-focus lens and a true telephoto lens: the telephoto lens uses a telephoto group to be physically shorter than its focal length.
The absolute value for the exposure time required depends on how sensitive to light the medium being used is (measured by the film speed, or, for digital media, by the quantum efficiency). Early photography used media that had very low light sensitivity, and so exposure times had to be long even for very bright shots. As technology has improved, so has the sensitivity through film cameras and digital cameras. See history of photography for more on this subject.
Other results from physical and geometrical optics apply to camera optics. For example, the maximum resolution capabilities of a particular camera set-up is determined by the diffraction limit associated with the pupil size and given, roughly, by the Rayleigh criterion.
Atmospheric optics
Main page: Category:Atmospheric optical phenomena
The unique optical properties of the atmosphere cause a wide range of spectacular optical phenomena. The blue color of the sky is a direct result of Rayleigh scattering which redirects higher frequency (blue) sunlight back into the field of view of the observer. Because blue light is scattered more easily than red light, the sun takes on a reddish hue when it is observed through a thick atmosphere, as during a sunrise or sunset. Additional particulate matter in the sky can scatter different colors at different angles creating colorful glowing skies at dusk and dawn. Scattering off of ice crystals and other particles in the atmosphere are responsible for halos, afterglows, coronas, rays of sunlight, and sun dogs. The variation in these kinds of phenomena are due to different particle sizes and geometries.
Mirages are another sort of optical phenomena due to variations in the refraction of light through the atmosphere. Other dramatic optical phenomena associated with this include the Novaya Zemlya effect where the sun appears to rise earlier than predicted with a distorted shape. A spectacular form of refraction occurs with a temperature inversion called the Fata Morgana where objects on the horizon or even beyond the horizon, such as islands, cliffs, ships or icebergs, appear elongated and elevated, like "fairy tale castles".
Rainbows are the result of a combination of optical effects: total internal reflection and dispersion of light in raindrops. A single reflection off the back of an array of raindrops produces a coherent rainbow with an angular size on the sky that ranges from 40 to 42 degrees with red on the outside. Double rainbows are produced by two internal reflections with angular size of 50.5 to 54 degrees with violet on the outside. Because rainbows must be seen with the sun 180 degrees away from the center of the rainbow, rainbows are more prominent the closer the sun is to the horizon.
References
- ^ McGraw-Hill Encyclopedia of Science and Technology (5th edition ed.). The McGraw-Hill Companies, Inc. 1993.
{{cite book}}:|edition=has extra text (help) - T. F. HOAD (1996). The Concise Oxford Dictionary of English Etymology.
- BBC News, "World's oldest telescope?"
- Cited in D. C. Lindberg, Theories of Vision from al-Kindi to Kepler, (Chicago: Univ. of Chicago Pr., 1976), p. 19.
- Lindberg, David C. (Winter 1971), "Alkindi's Critique of Euclid's Theory of Vision", Isis, 62 (4): 469–489 , doi:10.1086/350790
- R. Rashed, "A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses", Isis 81 (1990): 464–91.
- (Wade & Finger 2001) harv error: no target: CITEREFWadeFinger2001 (help)
- (Elliott, 1966 & Chapter 1) harv error: no target: CITEREFElliott1966Chapter_1 (help)
- O. S. Marshall (1950). "Alhazen and the Telescope", Astronomical Society of the Pacific Leaflets 6, p. 4.
- Bellis, Mary. "The History of Eye Glasses or Spectacles". About.com:Inventors. Retrieved 2007-09-01.
- Galileo's Telescope - by: Albert Van Helden
- Topdemir, Hüseyin Gazi (1999), Takîyüddîn'in Optik Kitabi, Ministry of Culture Press, Ankara
- Giambattista della Porta, (2005), Natural Magick, page 339. NuVision Publications, LLC.
- Stargazer By Fred Watson, Inc NetLibrary Page 109
- Microscopes: Time Line, Nobel Foundation, retrieved April 3, 2009
- Stephen Jay Gould(2000). The Lying Stones of Marrakech, ch.2 "The Sharp-Eyed Lynx, Outfoxed by Nature". London: Jonathon Cape. ISBN 0224050443
- ^ A. I. Sabra (1981). Theories of light, from Descartes to Newton. CUP Archive. ISBN 0521284368.
- Magie, William Francis (1935). A Source Book in Physics. Harvard University Press. p. 309
- James Clerk Maxwell, A Dynamical Theory of the Electromagnetic Field, Philosophical Transactions of the Royal Society of London 155, 459-512 (1865).
- For a solid approach to the complexity of Planck's intellectual motivations for the quantum, for his reluctant acceptance of its implications, see Helge Kragh, Max Planck: the reluctant revolutionary, Physics World. December 2000.
- Einstein, Albert (1905a), "On a Heuristic Viewpoint Concerning the Production and Transformation of Light" (PDF), Annalen der Physik, 17: 132–148. This annus mirabilis paper on the photoelectric effect was received by Annalen der Physik 18 March.
- 1913. "On the Constitution of Atoms and Molecules," Philosophical Magazine 26 (Series 6): 1-25. The landmark paper laying the Bohr model of the atom and molecular bonding.
- Taylor, Nick (2000). LASER: The inventor, the Nobel laureate, and the thirty-year patent war. New York: Simon & Schuster. ISBN 0-684-83515-0.
- Feynman, Richard (1985). "Chapter 1". QED: The Strange Theory of Light and Matter. Princeton University Press. p. 6.
- Maxwell, A Dynamical Theory of the Electromagnetic Field, 1864 5, page 499.
- Theo Koupelis and Karl F. Kuhn (2007). In Quest of the Universe. Jones & Bartlett Publishers. ISBN 0763743879.
- D. H. Delphenich (2006). "Nonlinear optical analogies in quantum electrodynamics". ArXiv preprint.
- Arthur Schuster, An Introduction to the Theory of Optics, London: Edward Arnold, 1904 online.
- Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. pp. 19–20. ISBN 0-8194-5294-7.
- Siegman, Anthony E. (1986). Lasers. University Science Books. ISBN 0-935702-11-3. Chapter 16.
- Albedo - from Eric Weisstein's World of Physics
- ^ Hugh D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.Chapter 35
- E. W. Marchand, Gradient Index Optics, New York, NY, Academic Press, 1978.
- ^ Hecht, Eugene (1987). Optics (2nd ed. ed.). Addison Wesley. ISBN 0-201-11609-X.
{{cite book}}:|edition=has extra text (help) Chapters 5 & 6. - ^ Hugh D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.Chapter 36
- "Introduction to Stereomicroscopy" by Paul E. Nothnagle, William Chambers, and Michael W. Davidson, Nikon MicroscopyU.
- ^ Longhurst RS, Geometrical and Physical Optics, 2nd Edition, 1968, Longmans
- Goodman, Joseph (2005). Introduction to Fourier Optics (3rd ed, ed.). Roberts & Co Publishers. ISBN 0974707724.
{{cite book}}: CS1 maint: extra punctuation (link) or online here - ^ Hugh D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.Chapter 37
- ^ Hariharan, P. (2003). Optical Interferometry (PDF) (2nd edition ed.). San Diego, USA: Academic Press.
{{cite book}}:|edition=has extra text (help) - Earl R. Hoover, Cradle of Greatness: National and World Achievements of Ohio’s Western Reserve (Cleveland: Shaker Savings Association, 1977).
- Jean Louis Aubert (1760). Memoires pour l'histoire des sciences et des beaux arts. Paris: Impr. de S. A. S.; Chez E. Ganeau. p. 149.
- Sir David Brewster (1831). A Treatise on Optics. London: Longman, Rees, Orme, Brown & Green and John Taylor. p. 95.
- Robert Hooke. "Micrographia: or, Some physiological descriptions of minute bodies made by magnifying glasses". London: J. Martyn and J. Allestry, 1665. (first edition).
- Turnbull, H. W. (1940–1941). "Early Scottish Relations with the Royal Society: I. James Gregory, F.R.S. (1638–1675)". Notes and Records of the Royal Society of London. 3: 22–38.
{{cite journal}}: Check date values in:|year=(help)CS1 maint: year (link) - Rothman, Tony (2003). Everything's Relative and Other Fables in Science and Technology. New Jersey: Wiley. ISBN 0471202576.
- ^ Hugh D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.Chapter 38
- Lucky Exposures: Diffraction limited astronomical imaging through the atmosphere by Robert Nigel Tubbs
- Bohren, Craig F. (1983). Absorption and Scattering of Light by Small Particles. Wiley. ISBN 0-471-29340-7.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Rajiv Ramaswami and Kumar N. Sivarajan, Optical Networks: A Practical Perspective (Academic Press: London 1998).
- Brillouin, Léon. Wave Propagation and Group Velocity. Academic Press Inc., New York (1960)
- Born, Max; Wolf, Emil (October 1999). Principle of Optics. Cambridge: Cambridge University Press. pp. 14–24. ISBN 0521642221.
- ^ Hugh D. Young (1992). University Physics 8e. Addison-Wesley. ISBN 0201529815.Chapter 34
- D. F. Walls and G. J. Milburn Quantum Optics (Springer 1994)
- Optical Computer Architectures: The Application of Optical Concepts to Next Generation Computers, Optical Computer Architectures: The Application of Optical Concepts to Next Generation Computers book by Alastair D. McAulay (1999)
- "SPIE society".
- Shen, Y. R. (1984). The principles of nonlinear optics. New York, Wiley-Interscience.
- "laser". Reference.com. Retrieved 2008-05-15.
- Charles H. Townes - Nobel Lecture
- Townes, Charles Hard. "The first laser". University of Chicago. Retrieved 2008-05-15.
- Charles H. Townes (2003). "The first laser". In Laura Garwin and Tim Lincoln (ed.). A Century of Nature: Twenty-One Discoveries that Changed Science and the World. University of Chicago Press. pp. 107–12. ISBN 0-226-28413-1.
{{cite book}}:|access-date=requires|url=(help); External link in|chapterurl=|chapterurl=ignored (|chapter-url=suggested) (help) - "Handheld barcode scanner technologies, illustrated".
- "How the CD was developed". BBC News. 2007-08-17. Retrieved 2007-08-17.
- Wilson, J. & Hawkes, J.F.B. (1987). Lasers: Principles and Applications, Prentice Hall International Series in Optoelectronics, Prentice Hall. ISBN 0-13-523697-5
- ^ David Atchison and George Smith (Feb, 2000). Optics of the Human Eye. Elsevier. ISBN 0-7506-3775-7.
{{cite book}}: Check date values in:|date=(help) - ^ Kandel, E. R. (2000). Principles of Neural Science (4th ed.). New York: McGraw-Hill. pp. 507–513. ISBN 0-8385-7701-6.
{{cite book}}: Cite has empty unknown parameters:|origmonth=,|month=,|chapterurl=, and|origdate=(help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ^ Meister, Darryl. "Ophthalmic Lens Design". OptiCampus.com. Retrieved November 12, 2008.
- Key to All Optical Illusions Discovered, Jeanna Bryner, Senior Writer, LiveScience.com 6/2/08.
- Geometry of the Vanishing Point at Convergence
- "The Moon Illusion Explained", Don McCready, University of Wisconsin-Whitewater
- Anil K. Jain, Mário Figueiredo, and Josiane Zerubia (editors) (2001). Energy Minimization Methods in Computer Vision and Pattern Recognition. Springer.
{{cite book}}:|author=has generic name (help)CS1 maint: multiple names: authors list (link) - Samuel Edward Sheppard and Charles Edward Kenneth Mees (1907). Investigations on the Theory of the Photographic Process. Longmans, Green and Co. p. 214.
- Bernhard J. Suess (2003). Mastering Black-and-White Photography. Allworth Communications. ISBN 1581153066.
- Michael John Langford (2000). Basic Photography. Focal Press. ISBN 0240515927.
- Leslie D. Stroebel (1999). View Camera Technique. Focal Press.
{{cite book}}: Unknown parameter|ibsn=ignored (help) - Photo.net how-to — Guide to macro photography
- Steve Simmons (1992). Using the View Camera (2, revised, illustrated ed.). Amphoto Books. p. 35. ISBN 0817463534.
- New York Times Staff (2004). The New York Times Guide to Essential Knowledge. Macmillan. ISBN 9780312313678.
- Richard R. Carlton, Arlene McKenna Adler (2000). Principles of Radiographic Imaging: An Art and a Science. Thomson Delmar Learning.
{{cite book}}: Unknown parameter|ibsn=ignored (help) - Crawford, William (1979). The Keepers of Light: A History and Working Guide to Early Photographic Processes. Dobbs Ferry, New York: Morgan & Morgan. p. 20. ISBN 0871001586.
- John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0 444 10791 6
- Ahrens, C. Donald (1994). Meteorology Today: an introduction to weather, climate, and the environment (5th ed.). St. Paul MN: West Publishing Company. pp. 88–89.
- An Introduction to Mirages by Andy Young
Textbooks
- Born, Max;Wolf, Emil. Principles of Optics (7th ed.). Pergamon Press, 1999.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Hecht, Eugene (2001). Optics (4th ed.). Pearson Education. ISBN 0-8053-8566-5.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 0-7167-0810-8.
- Lipson, Stephen G. (1995). Optical Physics (3rd ed.). Cambridge University Press. ISBN 0-5214-3631-1.
See also
|
|
External links
Textbooks and tutorials
- Optics — an open-source Optics textbook
- Optics2001 — Optics library and community
Wikibooks modules
|
|
Societies
|
Periodicals
| Major branches of physics | |
|---|---|
| Divisions | |
| Approaches | |
| Classical | |
| Modern | |
| Interdisciplinary | |
| Related | |

 is the wavelength and
is the wavelength and  is the frequency of the wave, a changing wavelength results in a changing
is the frequency of the wave, a changing wavelength results in a changing 
 ) and reflects off the surface at an angle with respect to normal called the
) and reflects off the surface at an angle with respect to normal called the  ). The law of reflection states
). The law of reflection states
 .
. ) and image distances (
) and image distances ( ) to the focal length (
) to the focal length ( ):
):
 .
. .
. and another medium with index of refraction
and another medium with index of refraction  . In such situations,
. In such situations, 
 and
and  are the angles between the normal (to the interface) plane and the incident waves respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:
are the angles between the normal (to the interface) plane and the incident waves respectively. This phenomenon is also associated with a changing speed of light as seen from the definition of index of refraction provided above which implies:

 and
and  are the wave velocities through the respective media.
are the wave velocities through the respective media.
 ):
):

 is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.
is the distance associated with the image and is considered by convention to be negative if on the same side of the lens as the object and positive if on the opposite side of the lens.

 nm) where the
nm) where the  . The bright fringes occur along lines where black lines intersect with black lines and white lines intersect with white lines. These fringes are separated by angle
. The bright fringes occur along lines where black lines intersect with black lines and white lines intersect with white lines. These fringes are separated by angle  and are numbered as order
and are numbered as order  .
.
 th order fringe, where the central maximum is
th order fringe, where the central maximum is  .
.




 is the
is the 


 is 1/2, the transmission coefficient becomes
is 1/2, the transmission coefficient becomes

 , and given by
, and given by

 is the diameter of the entrance pupil. By convention, "f/#" is treated as a single symbol, and specific values of f/# are written by replacing the
is the diameter of the entrance pupil. By convention, "f/#" is treated as a single symbol, and specific values of f/# are written by replacing the