Misplaced Pages

Revision as of 14:58, 3 October 2009

The negative impedance converter (NIC) is a configuration of an operational amplifier which acts as a negative load. This is achieved by introducing a phase shift of 180° (inversion) between the voltage and the current for any signal generator. The basic circuit of an NIC and its analysis is shown below.

Basic circuit and analysis

If the operational amplifier is ideal, this negative feedback configuration ensures that the inverting input matches the ${\displaystyle V_{s}}$ from the non-inverting input. Additionally, no current goes into the operational amplifier inputs, and so the current

${\displaystyle I_{2}={\frac {V_{s}}{R_{1}}}.}$

Hence, the voltage at the output of the operational amplifier

${\displaystyle V_{\text{opamp}}\triangleq V_{s}+I_{2}R_{2}=V_{s}+V_{s}{\frac {R_{2}}{R_{1}}}.}$

The current going from the operational amplifier output through resistor ${\displaystyle R_{3}}$ toward the source ${\displaystyle V_{s}}$ is ${\displaystyle -I_{s}}$, and

${\displaystyle -I_{s}={\frac {V_{\text{opamp}}-V_{s}}{R_{3}}}=V_{s}{\frac {\frac {R_{2}}{R_{1}}}{R_{3}}}.}$

So the input ${\displaystyle V_{s}}$ experiences an opposing current ${\displaystyle -I_{s}}$ that is proportional to ${\displaystyle V_{s}}$, and the circuit acts like a resistor with negative resistance

${\displaystyle R_{\text{in}}\triangleq {\frac {V_{s}}{I_{s}}}=-R_{3}{\frac {R_{1}}{R_{2}}}.}$

This result can also be shown using Kirchoff's voltage law. Moving from one ground to the other,

${\displaystyle \overbrace {(R_{1}+R_{2})I_{2}} ^{\text{Inverting input}}\,+\,\overbrace {R_{3}I_{s}} ^{R_{3}}\,-\,V_{s}=0.}$

So because ${\displaystyle I_{2}=V_{s}/R_{1}}$,

${\displaystyle V_{s}=-I_{s}R_{3}{\frac {R_{1}}{R_{2}}}}$,

which shows that the input resistance felt by the signal source ${\displaystyle V_{s}}$ is indeed

${\displaystyle R_{\text{in}}\triangleq {\frac {V_{s}}{I_{s}}}=-R_{3}{\frac {R_{1}}{R_{2}}}.}$

In general, elements ${\displaystyle R_{1}}$, ${\displaystyle R_{2}}$, and ${\displaystyle R_{3}}$ need not be pure resistances (i.e., they may be capacitors, inductors, or impedance networks).

Application

By using an NIC as a negative resistor, it is possible to let a real generator behave (almost) like an ideal generator, (i.e., the magnitude of the current or of the voltage generated does not depend on the load).

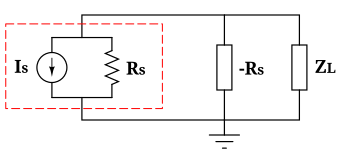
An example for a current source is shown in the figure on the right. The current generator and the resistor within the dotted line is the Norton representation of a circuit comprising a real generator and ${\displaystyle R_{s}}$ is its internal resistance. If an NIC is placed in parallel to that internal resistance, and the NIC has the same magnitude but inverted resistance value, there will be ${\displaystyle R_{s}}$ and ${\displaystyle -R_{s}}$ in parallel. Hence, the equivalent resistance is

${\displaystyle \lim \limits _{R_{\text{NIC}}\to R_{s}+}R_{s}\|(-R_{\text{NIC}})\triangleq \lim \limits _{R_{\text{NIC}}\to R_{s}+}{\frac {-R_{s}R_{\text{NIC}}}{R_{s}+-R_{\text{NIC}}}}=\infty .}$

That is, the real generator will now behave like an ideal one; its output voltage will be the same for any load ${\displaystyle Z_{L}}$. In particular, any current that is shunted away from the load into the Norton equivalent resistance ${\displaystyle R_{s}}$ will be supplied by the NIC instead.

The ideal behavior in this application depends upon the Norton resistance ${\displaystyle R_{s}}$ and the NIC resistance ${\displaystyle R_{\text{NIC}}}$ being matched perfectly. As long as ${\displaystyle R_{\text{NIC}}>R_{s}}$, the equivalent resistance of the combination will be greater than ${\displaystyle R_{s}}$; however, if ${\displaystyle R_{\text{NIC}}\gg R_{s}}$, then the impact of the NIC will be negligible. However, when

${\displaystyle {\frac {1}{R_{\text{NIC}}}}>{\frac {1}{R_{s}}}+{\frac {1}{R_{L}}},\quad {\text{(i.e., when}}\,R_{\text{NIC}}<R_{s}\|R_{L}{\text{)}}\,}$

the circuit is unstable (e.g., when ${\displaystyle R_{\text{NIC}}<R_{s}}$ in an unloaded system). In particular, the surplus current from the NIC generates positive feedback that causes the voltage driving the load to reach its power supply limits. By reducing the impedance of the load (i.e., by causing the load to draw more current), the generator–NIC system can be rendered stable again.

In principle, if the Norton equivalent current source was replaced with a Norton equivalent voltage source, a NIC of equivalent magnitude could be placed in series with the voltage source's series resistance. Any voltage drop across the series resistance would then be added back to the circuit by the NIC. However, a NIC implemented as above with an operational amplifier must terminate on an electrical ground, and so this use is not practical. Because any voltage source with nonzero series resistance can be represented as an equivalent current source with finite parallel resistance, an operational amplifier NIC will typically be placed in parallel with a source when used to improve the impedance of the source.

Negative impedance circuits

The negative of any impedance can be produced by a negative impedance converter, including negative capacitance and negative inductance.

References

1. Wai-Kai Chen, The Circuits and Filters Handbook, pp396-397, CRC Press, 2003 ISBN 0849309123.

See also

• Negative resistance
• Gyrator (which uses operational amplifier to implement an inductor with a capacitor)

External links

• Improved frequency modulator uses "Negatron", Belousov, Alexander, USA, EDN, 07/11/2002

• Electronic amplifiers