| Revision as of 07:13, 24 June 2010 editDatumizer (talk | contribs)Extended confirmed users, Pending changes reviewers42,788 edits rephrase image cap← Previous edit | Latest revision as of 20:03, 21 January 2025 edit undo91.234.125.131 (talk) Undid revision 1270900153 by 91.234.125.131 (talk)Tag: Undo | ||
| (880 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
| {{short description|Alternative representations of the RGB color model}} | |||
| ] | |||
| {{double image|right|HSL color solid cylinder alpha lowgamma.png|197|HSV color solid cylinder alpha lowgamma.png|197|HSL cylinder|HSV cylinder}} | |||
| ] | |||
| '''HSL''' and '''HSV''' are the two most common ] representations of points in an ], which rearrange the geometry of RGB in an attempt to be more ] relevant than the ] representation. They were developed in the 1970s for ] applications, and are used for ], in color-modification tools in ] software, and less commonly for ] and ]. | |||
| '''HSL''' and '''HSV''' are the two most common ] representations of points in an ]. The two representations rearrange the geometry of RGB in an attempt to be more intuitive and ] relevant than the ] (cube) representation. Developed in the 1970s for ] applications, HSL and HSV are used today in ], in ] software, and less commonly in ] and ]. | |||
| HSL stands for ''hue'', ''saturation'', and ''lightness'', and is often also called '''HLS'''. HSV stands for ''hue'', ''saturation'', and ''value'', and is also often called '''HSB''' (''B'' for ''brightness''). A third model, common in ] applications, is '''HSI''', for ''hue'', ''saturation'', and ''intensity''. Unfortunately, while typically consistent, these definitions are not standardized, and any of these abbreviations might be used for any of these three or several other related cylindrical models. (For technical definitions of these terms, see ].) | |||
| HSL stands for ''hue'', ''saturation'', and ''lightness'', and is often also called '''HLS'''. HSV stands for ''hue'', ''saturation'', and ''value'', and is also often called '''HSB''' (''B'' for ''brightness''). A third model, common in computer vision applications, is '''HSI''', for ''hue'', ''saturation'', and ''intensity''. However, while typically consistent, these definitions are not standardized, and any of these abbreviations might be used for any of these three or several other related cylindrical models. (For technical definitions of these terms, see ].) | |||
| In each cylinder, the angle around the central vertical axis corresponds to “hue”, the distance from the axis corresponds to “saturation”, and the distance along the axis corresponds to “lightness”, “value” or “brightness”. Note that while “hue” in HSL and HSV refers to the same attribute, their definitions of “saturation” differ dramatically. | |||
| Because HSL and HSV are simple transformations of device-dependent RGB models, the physical colors they define depend on the colors of the red, green, and blue ] of the device or of the particular RGB space, and on the ] used to represent the amounts of those primaries. Each unique RGB device therefore has unique HSL and HSV spaces to accompany it, and numerical HSL or HSV values describe a different color for each basis RGB space.<ref>See ].</ref> | In each cylinder, the angle around the central vertical axis corresponds to "]", the distance from the axis corresponds to "]", and the distance along the axis corresponds to "]", "value" or "]". Note that while "hue" in HSL and HSV refers to the same attribute, their definitions of "saturation" differ dramatically. Because HSL and HSV are simple transformations of device-dependent RGB models, the physical colors they define depend on the colors of the red, green, and blue ] of the device or of the particular RGB space, and on the ] used to represent the amounts of those primaries. Each unique RGB device therefore has unique HSL and HSV spaces to accompany it, and numerical HSL or HSV values describe a different color for each basis RGB space.<ref>See ].</ref> | ||
| Both of these representations are used widely in computer graphics, and one or the other of them is often more convenient than RGB, but both are also |
Both of these representations are used widely in computer graphics, and one or the other of them is often more convenient than RGB, but both are also criticized for not adequately separating color-making attributes, or for their lack of perceptual uniformity. Other more computationally intensive models, such as ] or ] are said to better achieve these goals. | ||
| == |
==Basic principle== | ||
| {{multiple image | |||
| {{double image|right|HSL color solid dblcone chroma gray.png|197|HSV color solid cone chroma gray.png|197|Fig. 2a–b. If we plot hue and (a) HSL lightness or (b) HSV value against chroma instead of saturation, the resulting solid is a ] or ], respectively, not a cylinder. Such diagrams often claim to represent HSL or HSV directly, with the chroma dimension mistakenly labeled “saturation”.}} | |||
| | align = right | |||
| | image1 = HSL color solid cylinder saturation gray.png | |||
| | width1 = 197 | |||
| | alt1 = | |||
| | caption1 = Fig. 2a. HSL cylinder. | |||
| | image2 = HSV color solid cylinder saturation gray.png | |||
| | width2 = 197 | |||
| | alt2 = | |||
| | caption2 = Fig. 2b. HSV cylinder. | |||
| | footer = | |||
| }} | |||
| HSL and HSV are both cylindrical geometries ({{nobr|fig. |
HSL and HSV are both cylindrical geometries ({{nobr|fig. 2}}), with hue, their angular dimension, starting at the ] ] at 0°, passing through the ] primary at 120° and the ] primary at 240°, and then wrapping back to red at 360°. In each geometry, the central vertical axis comprises the ''neutral'', ''achromatic'', or ''gray'' colors ranging, from top to bottom, white at lightness 1 (value 1) to black at lightness 0 (value 0). | ||
| In both geometries, the ] primary and ]s – red, ], green, ], blue and ] – and linear mixtures between adjacent pairs of them, sometimes called ''pure colors'', are arranged around the outside edge of the cylinder with saturation 1. These saturated colors have lightness 0.5 in HSL, while in HSV they have value 1. Mixing these pure colors with black – producing so-called '']'' – leaves saturation unchanged. In HSL, saturation is also unchanged by '']'' with white, and only mixtures with both black and white – called ''tones'' – have saturation less than 1. In HSV, tinting alone reduces saturation. | |||
| Because these definitions of saturation – in which very dark (in both models) or very light (in HSL) near-neutral colors, for instance {{colorsample2|#330000}} or {{nobr|{{colorsample2|#FFEEFF}},}} are considered fully saturated – conflict with the intuitive notion of color purity, often a conic or bi-conic solid is drawn instead ({{nobr|fig. 2}}), with what this article calls ''chroma'' as its radial dimension, instead of saturation. Confusingly, such diagrams usually label this radial dimension “saturation”, blurring or erasing the distinction between saturation and chroma.<ref>In Joblove and Greenberg’s (1978) paper first introducing HSL, they called HSL lightness “intensity”, called HSL saturation “relative chroma”, called HSV saturation “saturation” and called HSV value “value”. They carefully and unambiguously described and compared three models: hue/chroma/intensity, hue/relative chroma/intensity, and hue/value/saturation. Unfortunately, later authors were less fastidious, and current usage of these terms is inconsistent and often misleading.</ref> ], computing chroma is a helpful step in the derivation of each model. Because such an intermediate model – with dimensions hue, chroma, and HSV value or HSL lightness – takes the shape of a cone or bicone, HSV is often called the “hexcone model” while HSL is often called the “bi-hexcone model” (]).<ref>The name ''hexcone'' for hexagonal pyramid was coined in Smith (1978), and stuck.</ref> | |||
| {{multiple image | |||
| | align = right | |||
| | image1 = HSL color solid dblcone chroma gray.png | |||
| | width1 = 197 | |||
| | alt1 = | |||
| | caption1 = | |||
| | image2 = HSV color solid cone chroma gray.png | |||
| | width2 = 197 | |||
| | alt2 = | |||
| | caption2 = | |||
| | footer = Fig. 3a–b. If we plot hue and (a) HSL lightness or (b) HSV value against chroma (] of RGB values) rather than saturation (chroma over maximum chroma for that slice), the resulting solid is a ] or ], respectively, not a cylinder. Such diagrams often claim to represent HSL or HSV directly, with the chroma dimension confusingly labeled "saturation". | |||
| }} | |||
| Because these definitions of saturation – in which very dark (in both models) or very light (in HSL) near-neutral colors are considered fully saturated (for instance, {{colorsample2|#005456}} from the bottom right in the sliced HSL cylinder or {{colorsample2|#d4ffff}} from the top right) – conflict with the intuitive notion of color purity, often a ] or ] solid is drawn instead ({{nobr|fig. 3}}), with what this article calls '']'' as its radial dimension (equal to the ] of the RGB values), instead of saturation (where the saturation is equal to the chroma over the maximum chroma in that slice of the (bi)cone). Confusingly, such diagrams usually label this radial dimension "saturation", blurring or erasing the distinction between saturation and chroma.{{refn|group=upper-alpha |In the ] paper first introducing HSL, they called HSL lightness "intensity", called HSL saturation "relative chroma", called HSV saturation "saturation" and called HSV value "value". They carefully and unambiguously described and compared three models: hue/chroma/intensity, hue/relative chroma/intensity, and hue/value/saturation. Unfortunately, later authors were less fastidious, and current usage of these terms is inconsistent and often misleading.}} ], computing chroma is a helpful step in the derivation of each model. Because such an intermediate model – with dimensions hue, chroma, and HSV value or HSL lightness – takes the shape of a cone or bicone, HSV is often called the "hexcone model" while HSL is often called the "bi-hexcone model" (]).{{refn|group=upper-alpha |The name ''hexcone'' for hexagonal pyramid was coined in ], and stuck.}} | |||
| {{clear}} | {{clear}} | ||
| == |
==Motivation== | ||
| {{see also|Color theory|RGB color model|RGB color space}} | |||
| {{multiple image | {{multiple image | ||
| | align |
| align = right | ||
| | image1 |
| image1 = tint-tone-shade.svg | ||
| | width1 |
| width1 = 200 | ||
| | caption1 |
| caption1 = Fig. 4. Painters long mixed colors by combining relatively bright pigments with black and white. Mixtures with white are called ''tints'', mixtures with black are called ''shades'', and mixtures with both are called ''tones''. See ].<ref name=Levkowitz>]</ref> | ||
| | alt1 |
| alt1 = | ||
| | image2 |
| image2 = Ostwald.svg | ||
| | width2 |
| width2 = 200 | ||
| | caption2 |
| caption2 = Fig. 5. This 1916 color model by German chemist ] exemplifies the "mixtures with white and black" approach, organizing 24 "pure" colors into a ], and colors of each hue into a triangle. The model thus takes the shape of a bicone.<ref>Wilhelm Ostwald (1916). ''Die Farbenfibel''. Leipzig.</ref><ref>Wilhelm Ostwald (1918). ''Die Harmonie der Farben''. Leipzig.</ref> | ||
| | alt2 |
| alt2 = Several paint mixing terms can be arranged into a triangular arrangement: the left edge of the triangle shows ''white'' at its top and ''black'' at its bottom with ''gray'' between the two, each in its respective oval. A ''pure color'' (in this case, a bright blue-green) lies at the right corner of the triangle. On the edge between the pure color and black is a ''shade'' (a darker blue-green), between the pure color and white is a ''tint'' (a lighter, faded blue-green), and a ''tone'' lies in the middle of the triangle (a muted blue-green). | ||
| | image3 = Tektronix-hsl-patent-diagram.png | |||
| | width3 = 150 | |||
| | caption3 = Fig. 6. Tektronix graphics terminals used the earliest commercial implementation of HSL, in 1979. This diagram, from a patent filed in 1983, shows the bicone geometry underlying the model.<ref>Gar A. Bergstedt (April 1983). US patent 4694286, . Filed 1983-04-08. Issued 1987-09-15. Assigned to Tektronix, Inc.</ref> | |||
| | alt3 = In classic patent application style, this is a black-and-white diagram with the patent name, inventor name, and patent number listed at the top, shaded by crosshatching. This diagram shows a three-dimensional view of Tektronix’s biconic HSL geometry, made up of horizontal circular slices along a vertical axis expanded for ease of viewing. Within each circular slice, saturation goes from zero at the center to one at the margins, while hue is an angular dimension, beginning at blue with hue zero, through red with hue 120 degrees and green with hue 240 degrees, and back to blue. | |||
| }} | }} | ||
| {{multiple image | {{multiple image | ||
| | width |
| width = 200 | ||
| | image1 |
| image1 = RGB Cube Show lowgamma cutout a.png | ||
| | caption1 |
| caption1 = Fig. 6a. The RGB gamut can be arranged in a cube. | ||
| | alt1 |
| alt1 = The RGB cube has black at its origin, and the three dimensions R, G, and B pointed in orthogonal directions away from black. The corner in each of those directions is the respective primary color (red, green, or blue), while the corners further away from black are combinations of two primaries (red plus green makes yellow, red plus blue makes magenta, green plus blue makes cyan). At the cube's corner farthest from the origin lies white. Any point in the cube describes a particular color within the gamut of RGB. | ||
| | image2 |
| image2 = RGB Cube Show lowgamma cutout b.png | ||
| | caption2 |
| caption2 = Fig. 6b. The same image, with a portion removed for clarity. | ||
| | alt2 |
| alt2 = The same image, with a portion removed for clarity. | ||
| <!-- | <!-- | ||
| | image3 |
| image3 = RGB Cube Show lowgamma cutout c.png | ||
| --> | --> | ||
| }} | }} | ||
| {{multiple image | |||
| | align = right | |||
| | image3 = Tektronix-hsl-patent-diagram.png | |||
| | width3 = 300 | |||
| | caption3 = Fig. 7. Tektronix graphics terminals used the earliest commercial implementation of HSL, in 1979. This diagram, from a patent filed in 1983, shows the bicone geometry underlying the model.<ref>{{cite patent |inventor1-given=Gar A. |inventor1-surname=Bergstedt |country=US |number=4694286 |url=http://www.google.com/patents/about?id=WA8xAAAAEBAJ |status=patent |title=Apparatus and method for modifying displayed color images |fdate=1983-04-08 |pubdate=1987-09-15 |assign1= Tektronix, Inc }}</ref> | |||
| | alt3 = In classic patent application style, this is a black-and-white diagram with the patent name, inventor name, and patent number listed at the top, shaded by crosshatching. This diagram shows a three-dimensional view of Tektronix's biconic HSL geometry, made up of horizontal circular slices along a vertical axis expanded for ease of viewing. Within each circular slice, saturation goes from zero at the center to one at the margins, while hue is an angular dimension, beginning at blue with hue zero, through red with hue 120 degrees and green with hue 240 degrees, and back to blue. | |||
| }} | |||
| Most televisions, computer displays, and projectors produce colors by combining red, green, and blue light in varying intensities – the so-called ] ] ]s. The resulting mixtures in ] can reproduce a wide variety of colors (called a ]); however, the relationship between the constituent amounts of red, green, and blue light and the resulting color is unintuitive, especially for inexperienced users, and for users familiar with ] mixing of paints or traditional artists' models based on tints and shades ({{nobr|fig. 4}}). Furthermore, neither additive nor subtractive color models define color relationships the same way the ] does.{{refn|group=upper-alpha |For instance, a 1982 study by Berk, et al., found that users were better at describing colors in terms of HSL than RGB coordinates, after being taught both systems, but were much better still at describing them in terms of the natural-language CNS model (which uses names such as "very dark grayish yellow-green" or "medium strong bluish purple"). This shouldn't be taken as gospel however: a 1987 study by Schwarz, et al., found that users could match colors using RGB controls faster than with HSL controls; a 1999 study by Douglas and Kirkpatrick found that the visual feedback in the user interface mattered more than the particular color model in use, for user matching speed.<ref>{{cite journal|author1=Toby Berk |author2=Arie Kaufman |author3=Lee Brownston |date=August 1982 |title=A human factors study of color notation systems for computer graphics |journal=Communications of the ACM |volume=25 |issue=8 |pages=547–550 |doi=10.1145/358589.358606|s2cid=14838329 |doi-access=free }}</ref><ref>{{cite journal|author1=Michael W. Schwarz |author2=William B. Cowan |author3=John C. Beatty |date=April 1987 |title=An experimental comparison of RGB, YIQ, LAB, HSV, and opponent color models |journal=ACM Transactions on Graphics |volume=6 |issue=2 |pages=123–158 |doi=10.1145/31336.31338|s2cid=17287484 |doi-access=free }}</ref><ref>{{cite journal|author1=Sarah A. Douglas |author2=Arthur E. Kirkpatrick |date=April 1999 |title=Model and representation: the effect of visual feedback on human performance in a color picker interface |doi=10.1145/318009.318011 |journal=ACM Transactions on Graphics |volume=18 |issue=2 |pages= 96–127 |s2cid=14678328 |doi-access=free }}</ref>}} | |||
| For example, imagine we have an RGB display whose color is controlled by three ] ranging from {{nobr|0–255}}, one controlling the intensity of each of the red, green, and blue primaries. If we begin with a relatively colorful ] {{nobr|{{colorsample2|#D97621}}}}, with ] values {{nobr|1=''R'' = 217}}, {{nobr|1=''G'' = 118}}, {{nobr|1=''B'' = 33}}, and want to reduce its colorfulness by half to a less saturated orange {{nobr|{{colorsample2|#BA845C}}}}, we would need to drag the sliders to decrease ''R'' by 31, increase ''G'' by 24, and increase ''B'' by 59, as pictured below. | |||
| {{also|Color theory|RGB color model|RGB color space}} | |||
| Most televisions, computer displays, and projectors produce colors by combining red, green, and blue light in varying intensities – the so-called ] ] ]s. The resulting mixtures in ] can reproduce a wide variety of colors (called a ]); however, the relationship between the constituent amounts of red, green, and blue light and the resulting color is unintuitive, especially for inexperienced users, and for users familiar with ] mixing of paints or traditional artists’ models based on tints and shades ({{nobr|fig. 3}}). Furthermore, neither additive nor subtractive color models define color relationships the same way the ] does.<ref>For instance, a 1982 study by Berk, et al., found that users were better at describing colors in terms of HSL than RGB coordinates, after being taught both systems, but were much better still at describing them in terms of the natural-language CNS model (which uses names such as “very dark grayish yellow-green” or “medium strong bluish purple”). This shouldn’t be taken as gospel however: a 1987 study by Schwarz, et al., found that users could match colors using RGB controls faster than with HSL controls; a 1999 study by Douglas and Kirkpatrick found that the visual feedback in the user interface mattered more than the particular color model in use, for user matching speed.<br>Toby Berk, Arie Kaufman, and Lee Brownston (August 1982). . ''Communications of the ACM'' '''25'''(8): 547–550.<br>Michael W. Schwarz, William B. Cowan, and John C. Beatty (April 1987). ''ACM Transactions on Graphics'' '''6'''(2): 123–158.<br>Sarah A. Douglas and Arthur E. Kirkpatrick (April 1999). . ''ACM Transactions on Graphics'' '''18'''(2): 96–127.</ref> | |||
| ] | |||
| For example, imagine we have an RGB display whose color is controlled by three ] ranging from {{nobr|0–255}}, one controlling the intensity of each of the red, green, and blue primaries. If we begin with a relatively colorful ] {{nobr|{{colorsample2|#D97621}}}}, with ] values {{nobr|1=''R'' = 217}}, {{nobr|1=''G'' = 118}}, {{nobr|1=''B'' = 33}}, and want to reduce its colorfulness by half to a less saturated orange {{nobr|{{colorsample2|#BA845C}}}}, we would need to drag the sliders to decrease ''R'' by 31, increase ''G'' by 24, and increase ''B'' by 59, as pictured below. Needless to say, these numbers seem mostly arbitrary. | |||
| Beginning in the 1950s, ] broadcasts used a ] system whereby "]" and "]" signals were encoded separately, so that existing unmodified black-and-white televisions could still receive color broadcasts and show a monochrome image.<ref>The original patent on this idea was by ] in 1938: {{pb}} {{cite patent |country=FR |number=841335 |status=patent |title=Procédé de télévision en couleurs |fdate=1938-01-17 |gdate=1939-02-06 |pubdate=1939-05-17 |inventor1-surname=Valensi |inventor1-given=Georges}} {{pb}} {{cite patent |country=US |number=2375966 |status=patent |title=System of television in colors |fdate=1939-01-14 |pubdate=1945-05-15 |inventor1-surname=Valensi |inventor1-given=Georges}}</ref> | |||
| :] | |||
| In an attempt to accommodate more traditional and intuitive color mixing models, computer graphics pioneers at ] and ] |
In an attempt to accommodate more traditional and intuitive color mixing models, computer graphics pioneers at ] and ] introduced the HSV model for computer display technology in the mid-1970s, formally described by ]<ref name=Smith>]</ref> in the August 1978 issue of ]. In the same issue, Joblove and Greenberg<ref name=Joblove>]</ref> described the HSL model – whose dimensions they labeled ''hue'', ''relative chroma'', and ''intensity'' – and compared it to HSV ({{nobr|fig. 1}}). Their model was based more upon how colors are organized and conceptualized in ] in terms of other color-making attributes, such as hue, lightness, and chroma; as well as upon traditional color mixing methods – e.g., in painting – that involve mixing brightly colored pigments with black or white to achieve lighter, darker, or less colorful colors. | ||
| The following year, 1979, at ], ] introduced graphics terminals using HSL for color designation, and the Computer Graphics Standards Committee recommended it in their annual status report (fig. |
The following year, 1979, at ], ] introduced graphics terminals using HSL for color designation, and the Computer Graphics Standards Committee recommended it in their annual status report ({{nobr|fig. 7}}). These models were useful not only because they were more intuitive than raw RGB values, but also because the conversions to and from RGB were extremely fast to compute: they could run in real time on the hardware of the 1970s. Consequently, these models and similar ones have become ubiquitous throughout image editing and graphics software since then. Some of their uses are described ].<ref>] (August 2001). . Course at SIGGRAPH 2001.</ref><ref>{{cite journal|author=Ware Myers |date=July 1979|title=Interactive Computer Graphics: Flying High-Part I|journal=Computer|volume=12|issue=7|pages=8–17|doi=10.1109/MC.1979.1658808 |s2cid=15344162}}</ref><ref>{{cite journal|author1=N. Magnetat-Thalmann |author2=N. Chourot |author3=D. Thalmann |date=March 1984|title=Colour Gradation, Shading and Texture Using a Limited Terminal|doi=10.1111/j.1467-8659.1984.tb00092.x|journal=Computer Graphics Forum|volume=3|pages=83–90|s2cid=29541525 }}</ref><ref>{{cite journal|doi=10.1145/988497.988498|date= August 1979|last1=Computer Graphics Staff|title=Status report of the graphic standards planning committee |journal=ACM SIGGRAPH Computer Graphics|volume=13|issue=3|pages=1–10|s2cid=43687764}}</ref> | ||
| {{clear}} | {{clear}} | ||
| == |
==Formal derivation== | ||
| ] | |||
| === Color-making attributes === | |||
| {{also|Color vision}} | |||
| The dimensions of the HSV and HSL geometries – simple transformations of the not-perceptually-based RGB model – are not directly related to the ] color-making attributes of the same names, as defined by scientists such as the ] or ]. Nonetheless, it is worth reviewing those definitions before leaping into the derivation of our models.<ref>As Mark Fairchild says, “Clearly, if color appearance is to be described in a systematic, mathematical way, definitions of the phenomena being described need to be precise and universally agreed upon.” For the definitions of color-making attributes which follow, see:<br>Fairchild 2005, (this is the source of the direct quotations).<br>Kuehni 2003.<br>] (2009). . E284-09a.<br>] (1987). . Number 17.4. CIE, 4th edition. ISBN 978-3-900734-07-7.<br>Poynton 1997.<br>The sources in the linked Misplaced Pages articles.</ref> | |||
| ] | |||
| * '']'' is the “attribute of a visual sensation according to which an area appears to be similar to one of the ]: red, yellow, green, and blue, or to a combination of two of them”. | |||
| * ''Intensity'' or '']'' is the total amount of light passing through a particular area. | |||
| * '']'', denoted ''Y'' and measured in ], is the radiance weighted by the effect of each wavelength on a typical human observer. Often the term ''luminance'' is used for the relative luminance, ''Y''/''Y''<sub>''n''</sub>, where ''Y''<sub>''n''</sub> is the luminance of the reference ]. | |||
| * ] is the weighted sum of ] {{nobr|''R''′}}, {{nobr|''G''′}}, and {{nobr|''B''′}} values, denoted {{nobr|''Y''′}}, and used in ], for ] compression and video transmission. | |||
| * '']'' is the “attribute of a visual sensation according to which an area appears to emit more or less light”. | |||
| * '']'' or ''value'' is the “brightness relative to the brightness of a similarly illuminated white”. | |||
| * '']'' is the “attribute of a visual sensation according to which the perceived color of an area appears to be more or less chromatic”. | |||
| * ''Chroma'' is the “colorfulness relative to the brightness of a similarly illuminated white”. | |||
| * ''Saturation'' is the “colorfulness of a stimulus relative to its own brightness”. | |||
| ] | |||
| ''Brightness'' and ''colorfulness'' are absolute measures, which usually describe the ] of light entering the eye, while ''lightness'' and ''chroma'' are measured relative to some white point, and are thus often used for descriptions of surface colors, remaining roughly constant even as brightness and colorfulness change with different ]. Thus, saturation = colorfulness/brightness = chroma/lightness. | |||
| ] | |||
| === General approach === | |||
| HSL, HSV, and related models can be derived via geometric strategies, or can be thought of as specific instances of a “generalized LHS model”. The HSV and HSL model-builders took an RGB cube – with constituent amounts of red, green, and blue light in a color denoted {{nobr|1=''R'', ''G'', ''B'' ] ]]}}<ref>In Levkowitz and Herman’s (1993) formulation, ''R'', ''G'', and ''B'' stand for the voltages on the guns of a CRT display, which might have different maxima, and so their cartesian ] could be a box of any unequal dimensions. Other definitions commonly use integer values in the range {{nobr|}}, storing the value for each component in one ]. We define the RGB gamut to be a ] for convenience, because it simplifies and clarifies the math. Also, in general, HSL and HSV are today computed directly from ] {{nobr|''R''′}}, {{nobr|''G''′}}, and {{nobr|''B''′}} – for instance in ] space – but, when the models were developed, might have been transformations of a linear RGB space. Early authors don’t address gamma correction at all. We will drop the primes, and the labels ''R'', ''G'', and ''B'' should be taken to stand for the three attributes of the origin RGB space, whether or not it is gamma corrected.</ref> – and tilted it on its corner, so that black rested at the origin with white directly above it along the vertical axis, then measured the hue of the colors in the cube by their angle around that axis, starting with red at 0°. Then they came up with a characterization of brightness/value/lightness, and defined saturation to range from 0 along the axis to 1 at the most colorful point for each pair of other parameters.<ref>Levkowitz and Herman 1993.<br>Smith 1978.<br>Joblove and Greenberg 1978.</ref> | |||
| === |
===Color-making attributes=== | ||
| {{see also|Color vision}} | |||
| ] | |||
| The dimensions of the HSL and HSV geometries – simple transformations of the not-perceptually-based RGB model – are not directly related to the ] color-making attributes of the same names, as defined by scientists such as the ] or ]. Nonetheless, it is worth reviewing those definitions before leaping into the derivation of our models.{{refn|group=upper-alpha |"Clearly, if color appearance is to be described in a systematic, mathematical way, definitions of the phenomena being described need to be precise and universally agreed upon."<ref name=Fairchild-term>], </ref>}} For the definitions of color-making attributes which follow, see:<ref name=Fairchild-term/><ref name=Kuehni>]</ref><ref>{{cite book |publisher=] |date=2009 |url=http://www.astm.org/Standards/E284.htm |title=Standard Terminology of Appearance E284}}</ref><ref>{{cite book |publisher=] and ] |date=1987 |url=http://www.cie.co.at/publ/abst/17-4-89.html |title=International Lighting Vocabulary |edition=4th |isbn=978-3-900734-07-7 |access-date=2010-02-05 |archive-url=https://web.archive.org/web/20100227034508/http://www.cie.co.at/publ/abst/17-4-89.html |archive-date=2010-02-27 |url-status=dead }}</ref><ref name=Poynton>]</ref><ref>{{cite book |title=Digital Color Imaging Handbook |last=Sharma |first=G.|year=2003 |publisher=CRC Press |location=Boca Raton, FL |isbn=978-0-8493-0900-7 }}</ref> | |||
| In each of our models, we calculate both ''hue'' and what we’ll call ''chroma'', after Joblove and Greenberg, in the same way – that is, the hue of a color has the same numerical values in all of these models, as does its chroma. If we take our tilted RGB cube, and ] it onto the “chromaticity ]” ] to the neutral axis, our projection takes the shape of a hexagon, with red, yellow, green, cyan, blue, and magenta at its corners ({{nobr|fig. 8}}). ''Hue'' is roughly to the angle of the ] to a point in the projection, with red at 0°, while ''chroma'' is roughly the distance of the point from the origin.<ref>Using the ''chroma'' here not only agrees with the original Joblove and Greenberg (1978) paper, but is also in the proper spirit of the psychometric definition of the term. Some models call this attribute ''saturation'' – for instance ]’s “Saturation” blend mode – but such use is even more confusing than the use of the term in HSL or HSV, especially when two substantially different definitions are used side by side.</ref><ref>Most of the computer graphics papers and books discussing HSL or HSV have a formula or algorithm describing them formally. Our formulas which follow are some mix of those. See, for instance, Agoston 2005, or Foley, et al., 1995.</ref> | |||
| ; ]: The "attribute of a visual sensation according to which an area appears to be similar to one of the ]: red, yellow, green, and blue, or to a combination of two of them".<ref name=Fairchild-term/> | |||
| More precisely, both hue and chroma in this model are defined with respect to the hexagonal shape of the projection. The ''chroma'' is the proportion of the distance from the origin to the edge of the hexagon. In the lower part of the diagram to the right, this is the ratio of lengths {{nobr|''OP''/''OP''′}}, or alternately the ratio of the radii of the two hexagons. This ratio is the difference between the largest and smallest values of ''R'', ''G'', and ''B'' in a color. To make our definitions easier to write, we’ll define these maximum and minimum component values as ''M'' and ''m'', respectively.<ref>Hanbury and Serra put a great deal of effort into explaining why what we call ''chroma'' here can be written as {{nobr|max(''R'', ''G'', ''B'') − min(''R'', ''G'', ''B''}}), and showing that this value is a ]. They reserve the name ''chroma'' for the ] ] in the chromaticity plane (our ''C''<sub>2</sub>), and call this hexagonal distance ''saturation'' instead, as part of their IHLS model:<br>Allan Hanbury and Jean Serra (December 2002). “A 3D-polar Coordinate Colour Representation Suitable for Image Analysis”. Pattern Recognition and Image Processing Group Technical Report 77. Vienna, Austria: Vienna University of Technology.</ref> | |||
| ; ] (''L''<sub>e,Ω</sub>): The ] of light passing through a particular surface per unit ] per unit projected area, measured in ] in ] per ] per ] ({{nobreak|W·sr<sup>−1</sup>·m<sup>−2</sup>}}). | |||
| ; ] (''Y'' or ''L''<sub>v,Ω</sub>): The radiance weighted by the effect of each wavelength on a typical human observer, measured in SI units in ] ({{nobreak|cd/m<sup>2</sup>}}). Often the term ''luminance'' is used for the ], ''Y''/''Y''<sub>''n''</sub>, where ''Y''<sub>''n''</sub> is the luminance of the reference ]. | |||
| ; ] (''{{prime|Y}}''): The weighted sum of ] {{nobr|''{{prime|R}}''}}, {{nobr|''{{prime|G}}''}}, and {{nobr|''{{prime|B}}''}} values, and used in ], for ] compression and video transmission. | |||
| ; ]: The "attribute of a visual sensation according to which an area appears to emit more or less light".<ref name=Fairchild-term/> | |||
| ; ]: The "brightness relative to the brightness of a similarly illuminated white".<ref name=Fairchild-term/> | |||
| ; ]: The "attribute of a visual sensation according to which the perceived color of an area appears to be more or less chromatic".<ref name=Fairchild-term/> | |||
| ; ]: The "colorfulness relative to the brightness of a similarly illuminated white".<ref name=Fairchild-term/> | |||
| ; ]: The "colorfulness of a stimulus relative to its own brightness".<ref name=Fairchild-term/> | |||
| ''Brightness'' and ''colorfulness'' are absolute measures, which usually describe the ] of light entering the eye, while ''lightness'' and ''chroma'' are measured relative to some white point, and are thus often used for descriptions of surface colors, remaining roughly constant even as brightness and colorfulness change with different ]. ''Saturation'' can be defined as either the ratio of colorfulness to brightness, or that of chroma to lightness. | |||
| :<math>\begin{align} | |||
| M &= \operatorname{max}(R, G, B) \\ | |||
| m &= \operatorname{min}(R, G, B) \\ | |||
| C &= M - m | |||
| \end{align}</math> | |||
| ===General approach=== | |||
| To understand why chroma can be written as {{nobr|''M'' − ''m''}}, notice that any neutral color, with {{nobr|1=''R'' = ''G'' = ''B''}}, projects onto the origin and so has 0 chroma. Thus if we add or subtract the same amount from all three of ''R'', ''G'', and ''B'', we move vertically within our tilted cube, and do not change the projection. Therefore, the two colors {{nobr|(''R'', ''G'', ''B'')}} and {{nobr|(''R'' − ''m'', ''G'' − ''m'', ''B'' − ''m'')}} project on the same point, and have the same chroma. The chroma of a color with one of its components equal to zero {{nobr|1=(''m'' − ''m'' = 0)}} is simply the maximum of the other two components. This is {{nobr|''M'' − ''m''}}. | |||
| HSL, HSV, and related models can be derived via geometric strategies, or can be thought of as specific instances of a "generalized LHS model". The HSL and HSV model-builders took an RGB cube – with constituent amounts of red, green, and blue light in a color denoted {{nobr|1=''R'', ''G'', ''B'' ] ]]}}{{refn|group=upper-alpha |In ] formulation, ''R'', ''G'', and ''B'' stand for the voltages on the guns of a CRT display, which might have different maxima, and so their cartesian ] could be a box of any unequal dimensions. Other definitions commonly use integer values in the range {{nobr|}}, storing the value for each component in one ]. We define the RGB gamut to be a ] for convenience because it simplifies and clarifies the math. Also, in general, HSL and HSV are today computed directly from ] {{nobr|''{{prime|R}}''}}, {{nobr|''{{prime|G}}''}}, and {{nobr|''{{prime|B}}''}} – for instance in ] space – but, when the models were developed, might have been transformations of a linear RGB space. Early authors don't address gamma correction at all, except ]<ref name=Smith>]</ref> who clearly states that "We shall assume that an RGB monitor is a linear device", and thus designed HSV using linear RGB. We will drop the primes, and the labels ''R'', ''G'', and ''B'' should be taken to stand for the three attributes of the origin RGB space, whether or not it is gamma corrected.}} – and tilted it on its corner, so that black rested at the origin with white directly above it along the vertical axis, then measured the hue of the colors in the cube by their angle around that axis, starting with red at 0°. Then they came up with a characterization of brightness/value/lightness, and defined saturation to range from 0 along the axis to 1 at the most colorful point for each pair of other parameters.<ref name=Levkowitz/><ref name=Smith/><ref name=Joblove/> | |||
| ===Hue and chroma=== | |||
| The ''hue'' is the proportion of the distance around the edge of the hexagon which passes through the projected point, originally measured on the range {{nobr|] {{nobr|]:<ref>In the following, the multiplication of hue by 60° – that is, 360°/6 – can be seen as the hexagonal-geometry analogue of the conversion from ] to degrees, a multiplication by 360°/2''π'': the circumference of a ] is 2''π''; the circumference of a unit hexagon is 6.</ref> | |||
| {{see also|Hue|Chrominance}} | |||
| ] | |||
| In each of our models, we calculate both ''hue'' and what this article will call ], after Joblove and Greenberg (1978), in the same way – that is, the hue of a color has the same numerical values in all of these models, as does its chroma. If we take our tilted RGB cube, and ] it onto the "chromaticity ]" ] to the neutral axis, our projection takes the shape of a hexagon, with red, yellow, green, cyan, blue, and magenta at its corners ({{nobr|fig. 9}}). ''Hue'' is roughly the angle of the ] to a point in the projection, with red at 0°, while ''chroma'' is roughly the distance of the point from the origin.{{refn|group=upper-alpha |Using the ''chroma'' here not only agrees with the original ] paper, but is also in the proper spirit of the psychometric definition of the term. Some models call this attribute ''saturation'' – for instance ]'s "Saturation" blend mode – but such use is even more confusing than the use of the term in HSL or HSV, especially when two substantially different definitions are used side by side.}}{{refn|group=upper-alpha |name=formulasources|Most of the computer graphics papers and books discussing HSL or HSV have a formula or algorithm describing them formally. Our formulas which follow are some mix of those. See, for instance, ] or ]}} | |||
| :<math>\begin{align} | |||
| H^\prime &= | |||
| \begin{cases} | |||
| \mathrm{undefined}, &\mbox{if } C = 0 \\ | |||
| \frac{G - B}{C} \;\bmod 6, &\mbox{if } M = R \\ | |||
| \frac{B - R}{C} + 2, &\mbox{if } M = G \\ | |||
| \frac{R - G}{C} + 4, &\mbox{if } M = B | |||
| \end{cases} \\ | |||
| H &= 60^\circ \times H^\prime | |||
| \end{align}</math> | |||
| More precisely, both hue and chroma in this model are defined with respect to the hexagonal shape of the projection. The ''chroma'' is the proportion of the distance from the origin to the edge of the hexagon. In the lower part of the adjacent diagram, this is the ratio of lengths {{nobr|''OP''/''{{prime|OP}}''}}, or alternatively the ratio of the radii of the two hexagons. This ratio is the difference between the largest and smallest values among ''R'', ''G'', or ''B'' in a color. To make our definitions easier to write, we'll define these maximum, minimum, and chroma component values as ''M'', ''m'', and ''C'', respectively.{{refn|group=upper-alpha |] put a great deal of effort into explaining why what we call ''chroma'' here can be written as {{nobr|max(''R'', ''G'', ''B'') − min(''R'', ''G'', ''B''}}), and showing that this value is a ]. They reserve the name ''chroma'' for the ] in the chromaticity plane (our ''C''<sub>2</sub>), and call this hexagonal distance ''saturation'' instead, as part of their IHLS model}} | |||
| Sometimes, neutral colors (i.e. with {{nobr|1=''C'' = 0}}) are assigned a hue of 0° for convenience of representation. | |||
| : <math>M = \max(R, G, B)</math> | |||
| : <math>m = \min(R, G, B)</math> | |||
| : <math>C = \operatorname{range}(R, G, B) = M - m</math> | |||
| To understand why chroma can be written as {{nobr|''M'' − ''m''}}, notice that any neutral color, with {{nobr|1=''R'' = ''G'' = ''B''}}, projects onto the origin and so has 0 chroma. Thus if we add or subtract the same amount from all three of ''R'', ''G'', and ''B'', we move vertically within our tilted cube, and do not change the projection. Therefore, any two colors of {{nobr|(''R'', ''G'', ''B'')}} and {{nobr|(''R'' − ''m'', ''G'' − ''m'', ''B'' − ''m'')}} project on the same point, and have the same chroma. The chroma of a color with one of its components equal to zero {{nobr|1=(''m'' = 0)}} is simply the maximum of the other two components. This chroma is ''M'' in the particular case of a color with a zero component, and {{nobr|''M'' − ''m''}} in general. | |||
| ] | |||
| These definitions amount to a geometric warping of hexagons into circles: each side of the hexagon is mapped linearly onto a 60° arc of the circle ({{nobr|{{nobr|fig. 9}}}}). After such a transformation, hue is precisely the angle around the origin and chroma the distance from the origin: the angle and magnitude of the ] pointing to a color. | |||
| The ''hue'' is the proportion of the distance around the edge of the hexagon which passes through the projected point, originally measured on the range {{nobr|}} but now typically measured in ] {{nobr|]:{{refn|group=upper-alpha |In the following, the multiplication of hue by 60° – that is, 360°/6 – can be seen as the hexagonal-geometry analogue of the conversion from ]s to degrees, a multiplication by 360°/2''π'': the circumference of a ] is 2''π''; the circumference of a unit hexagon is 6.}} | |||
| ] | |||
| : <math>H' = \begin{cases} | |||
| Sometimes for image analysis applications, this hexagon-to-circle transformation is skipped, and ''hue'' and ''chroma'' (we’ll denote these ''H''<sub>2</sub> and ''C''<sub>2</sub>) are defined by the usual cartesian-to-polar coordinate transformations ({{nobr|fig. 10}}). The easiest way to derive those is via a pair of cartesian chromaticity coordinates which we’ll call ''α'' and ''β'':<ref>Hanbury and Serra (2002)<br>Allan Hanbury (March 2008). . ''Pattern Recognition Letters'' '''29'''(4): 494–500<br>Patrick Lambert and Thierry Carron (1999). “Symbolic fusion of luminance-hue-chroma features for region segmentation.” ''Pattern Recognition'' '''32''': 1857–1872.</ref> | |||
| \mathrm{undefined}, &\text{if } C = 0 \\ | |||
| \frac{G - B}{C} \bmod 6, &\text{if } M = R \\ | |||
| \frac{B - R}{C} + 2, &\text{if } M = G \\ | |||
| \frac{R - G}{C} + 4, &\text{if } M = B | |||
| \end{cases}</math> | |||
| : <math>H = 60^\circ \times H'</math> | |||
| Sometimes, neutral colors (i.e. with {{nobr|1=''C'' = 0}}) are assigned a hue of 0° for convenience of representation. | |||
| :<math>\begin{align} | |||
| \alpha &= \textstyle{\frac{1}{2}}(2R - G - B) \\ | |||
| \beta &= \textstyle{\frac{\sqrt{3}}{2}}(G - B) \\ | |||
| H_2 &= \operatorname{atan2}(\beta, \alpha) \\ | |||
| C_2 &= \sqrt{\alpha^2 + \beta^2} | |||
| \end{align}</math> | |||
| ] | |||
| (The ] function, a “two-argument arctangent”, computes the angle from a cartesian coordinate pair.) | |||
| These definitions amount to a geometric warping of hexagons into circles: each side of the hexagon is mapped linearly onto a 60° arc of the circle ({{nobr|fig. 10}}). After such a transformation, hue is precisely the angle around the origin and chroma the distance from the origin: the angle and magnitude of the ] pointing to a color. | |||
| Notice that these two definitions of hue (''H'' and ''H''<sub>2</sub>) nearly coincide, with a maximum difference between them for any color of about 1.12° – which occurs at twelve particular hues, for instance {{nobr|1=''H'' = 13.38°}}, {{nobr|1=''H''<sub>2</sub> = 12.26°}} – and with {{nobr|1=''H'' = ''H''<sub>2</sub>}} for every multiple of 30°. The two definitions of chroma (''C'' and ''C''<sub>2</sub>) differ more substantially: they are equal at the corners of our hexagon, but at points halfway between two corners, such as {{nobr|1=''H'' = ''H''<sub>2</sub> = 30°}}, we have {{nobr|1=''C'' = 1}}, but {{nobr|1=''C''<sub>2</sub> = {{radic|¾}} ≈ 0.866}}, a difference of about 13.4%. | |||
| {{clear}} | |||
| ] | |||
| === Lightness === | |||
| Sometimes for image analysis applications, this hexagon-to-circle transformation is skipped, and ''hue'' and ''chroma'' (we'll denote these ''H''<sub>2</sub> and ''C''<sub>2</sub>) are defined by the usual cartesian-to-polar coordinate transformations ({{nobr|fig. 11}}). The easiest way to derive those is via a pair of cartesian chromaticity coordinates which we'll call ''α'' and ''β'':<ref name=Hanbury2002>]</ref><ref name=Hanbury2008>]</ref><ref>{{cite journal|author1=Patrick Lambert |author2=Thierry Carron |doi=10.1016/S0031-3203(99)00010-2|title=Symbolic fusion of luminance-hue-chroma features for region segmentation|year=1999|journal=Pattern Recognition|volume=32|issue=11|pages=1857|bibcode=1999PatRe..32.1857L }}</ref> | |||
| ] | |||
| : <math>\alpha = R - G \cdot \cos(60^{\circ}) - B \cdot \cos(60^{\circ}) = \tfrac{1}{2}(2R - G - B)</math> | |||
| : <math>\beta = G \cdot \sin(60^{\circ}) - B \cdot \sin(60^{\circ}) = \tfrac{\sqrt{3}}{2}(G - B)</math> | |||
| : <math>H_2 = \operatorname{atan2}(\beta, \alpha)</math> | |||
| : <math>C_2 = \operatorname{gmean}(\alpha, \beta) = \sqrt{\alpha^2 + \beta^2}</math> | |||
| (The ] function, a "two-argument arctangent", computes the angle from a cartesian coordinate pair.) | |||
| Notice that these two definitions of hue (''H'' and ''H''<sub>2</sub>) nearly coincide, with a maximum difference between them for any color of about 1.12° – which occurs at twelve particular hues, for instance {{nobr|1=''H'' = 13.38°}}, {{nobr|1=''H''<sub>2</sub> = 12.26°}} – and with {{nobr|1=''H'' = ''H''<sub>2</sub>}} for every multiple of 30°. The two definitions of chroma (''C'' and ''C''<sub>2</sub>) differ more substantially: they are equal at the corners of our hexagon, but at points halfway between two corners, such as {{nobr|1=''H'' = ''H''<sub>2</sub> = 30°}}, we have {{math|1=''C'' = 1}}, but <math display="inline">C_2 = \sqrt{\frac{3}{4}} \approx 0.866,</math> a difference of about 13.4%. | |||
| While the definition of ''hue'' is relatively uncontroversial – it roughly satisfies the criterion that colors of the same perceived hue should have the same numerical hue – the definition of a ''lightness'' or ''value'' dimension is less obvious: there are several possibilities depending on the purpose and goals of the representation. Here are four of the most common ({{nobr|fig. 11}}; three of these are also shown in ]): | |||
| ==={{Anchor|Lightness|Value|Brightness|Intensity}} Lightness=== | |||
| * The simplest definition is just the average of the three components, in the HSI model called ''intensity'' ({{nobr|fig. 11a}}). This is simply the projection of a point onto the neutral axis – the vertical height of a point in our tilted cube. The advantage is that, together with Euclidean-distance calculations of hue and chroma, this representation preserves distances and angles from the geometry of the RGB cube.<ref>For instance, see:<br>Hanbury 2008.<br>Rafael C. Gonzalez and Richard Eugene Woods (2008). ''Digital Image Processing'', 3rd ed. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-168728-X. .</ref> | |||
| *:<math>I = \textstyle{\frac{1}{3}}(R + G + B)\,\!</math> | |||
| ] | |||
| * In the HSV “hexcone” model, ''value'' is defined as the largest component of a color, our ''M'' above ({{nobr|fig. 11b}}). This places all three primaries, and also all of the “secondary colors” – cyan, yellow, and magenta – into a plane with white, forming a ] out of the RGB cube.<ref>Smith 1978.</ref> | |||
| *:<math>V = M\,\!</math> | |||
| While the definition of ''hue'' is relatively uncontroversial – it roughly satisfies the criterion that colors of the same perceived hue should have the same numerical hue – the definition of a ''lightness'' or ''value'' dimension is less obvious: there are several possibilities depending on the purpose and goals of the representation. Here are four of the most common ({{nobr|fig. 12}}; three of these are also shown in ]): | |||
| * In the HSL “bi-hexcone” model, ''lightness'' is defined as the average of the largest and smallest color components ({{nobr|fig. 11c}}). This definition also puts the primary and secondary colors into a plane, but a plane passing halfway between white and black. The resulting color solid is a double-cone similar to Ostwald’s, ].<ref>Joblove and Greenberg 1978.</ref> | |||
| *:<math>L = \textstyle{\frac{1}{2}}(M + m)\,\!</math> | |||
| * The simplest definition is just the ], i.e. average, of the three components, in the HSI model called ''intensity'' ({{nobr|fig. 12a}}). This is simply the projection of a point onto the neutral axis – the vertical height of a point in our tilted cube. The advantage is that, together with Euclidean-distance calculations of hue and chroma, this representation preserves distances and angles from the geometry of the RGB cube.<ref name=Hanbury2008/><ref>Rafael C. Gonzalez and Richard Eugene Woods (2008). ''Digital Image Processing'', 3rd ed. Upper Saddle River, NJ: Prentice Hall. {{ISBN|0-13-168728-X}}. .</ref> | |||
| * A more perceptually relevant alternative is to use ], {{nobr|''Y''′}}, as a lightness dimension ({{nobr|fig. 11d}}). Luma is the weighted average of gamma-corrected ''R'', ''G'', and ''B'', based on their contribution to perceived luminance, long used as the monochromatic dimension in color television broadcast. For the ] primaries used in ], {{nobr|1=''Y''′<sub>709</sub> = .21''R'' + .72''G'' + .07''B''}}; for the ] ] primaries, {{nobr|1=''Y''′<sub>601</sub> = .30''R'' + .59''G'' + .11''B''}}; for other primaries different coefficients should be used.<ref>Poynton 1997. For a more specific discussion of the term ''luma'', see:<br>Charles Poynton (1999). . ''www.poynton.com''. Accessed January 2010.</ref><ref>See also ]. Photoshop exclusively uses the NTSC coefficients for its “Luminosity” blend mode regardless of the RGB color space involved. See:<br>Bruce Lindbloom (2001-09-25). . ''colorsync-users mailing list''.</ref> | |||
| *: <math>I = \operatorname{avg}(R, G, B) = \tfrac{1}{3}(R + G + B)</math> | |||
| *:<math>Y^\prime_{601} = .30R + .59G + .11B\,\!</math><!-- The \,\! is to keep the formula rendered as PNG instead of HTML. See Help:Math discussion on rendering of ^\prime vs \prime in PNG and HTML. Note that \, or \; do not disable HTML output by themselves for all browsers/MathML settings. --> | |||
| * In the HSV "hexcone" model, ''value'' is defined as the largest component of a color, our ''M'' above ({{nobr|fig. 12b}}). This places all three primaries, and also all of the "secondary colors" – cyan, yellow, and magenta – into a plane with white, forming a ] out of the RGB cube.<ref name=Smith/> | |||
| *: <math>V = \max(R, G, B) = M</math> | |||
| * In the HSL "bi-hexcone" model, ''lightness'' is defined as the average of the largest and smallest color components ({{nobr|fig. 12c}}), i.e. the ] of the RGB components. This definition also puts the primary and secondary colors into a plane, but a plane passing halfway between white and black. The resulting color solid is a double-cone similar to Ostwald's, ].<ref name=Joblove/> | |||
| *: <math>L = \operatorname{mid}(R, G, B) = \tfrac{1}{2}(M + m)</math> | |||
| * A more perceptually relevant alternative is to use ], {{nobr|''{{prime|Y}}''}}, as a lightness dimension ({{nobr|fig. 12d}}). Luma is the ] of gamma-corrected ''R'', ''G'', and ''B'', based on their contribution to perceived lightness, long used as the monochromatic dimension in color television broadcast. For ], the ] primaries yield {{nobr|''{{prime|Y}}''<sub>709</sub>}}, digital ] uses {{nobr|''{{prime|Y}}''<sub>601</sub>}} according to ] and some other primaries are also in use which result in different coefficients.<ref>]. </ref>{{refn|group=upper-alpha |For a more specific discussion of the term ''luma'', see Charles ]. See also ]. Photoshop exclusively uses the NTSC coefficients for its "Luminosity" blend mode regardless of the RGB color space involved.<ref>Bruce Lindbloom (2001-09-25). http://lists.apple.com/archives/colorsync-users/2001/Sep/msg00488.html {{Webarchive|url=https://web.archive.org/web/20110707173255/http://lists.apple.com/archives/colorsync-users/2001/Sep/msg00488.html |date=2011-07-07 }} "Re: Luminosity channel...".</ref>}} | |||
| *: <math>Y'_\text{601} = 0.299\cdot R + 0.587\cdot G + 0.114\cdot B</math> (SDTV)<!--525 lines--> | |||
| *: <math>Y'_\text{240} = 0.212\cdot R + 0.701\cdot G + 0.087\cdot B</math> ]<!--also SMPTE 145--> | |||
| *: <math>Y'_\text{709} = 0.2126\cdot R + 0.7152\cdot G + 0.0722\cdot B</math> ] | |||
| *: <math>Y'_\text{2020} = 0.2627\cdot R + 0.6780\cdot G + 0.0593\cdot B</math> ]<!--also Rec. 2100--> | |||
| All four of these leave the neutral axis alone. That is, for colors with {{nobr|1=''R'' = ''G'' = ''B''}}, any of the four formulations yields a lightness equal to the value of ''R'', ''G'', or ''B''. | All four of these leave the neutral axis alone. That is, for colors with {{nobr|1=''R'' = ''G'' = ''B''}}, any of the four formulations yields a lightness equal to the value of ''R'', ''G'', or ''B''. | ||
| For a graphical comparison, see ]. | For a graphical comparison, see ]. | ||
| {{clear}} | {{clear}} | ||
| === |
===Saturation=== | ||
| }} for every combination of hue and lightness or value.]] | |||
| If we encode colors in a hue/lightness/chroma or hue/value/chroma model (using the definitions from the previous two sections), not all combinations of value (or lightness) and chroma are meaningful: that is, half of the colors we can describe using {{nobr|''H'' ∈ }}, and {{nobr|''V'' ∈ }} fall outside the RGB gamut (the gray parts of the slices in the image to the right). The creators of these models considered this a problem for some uses. For example, in a color selection interface with two of the dimensions in a rectangle and the third on a slider, half of that rectangle is made of unused space. Now imagine we have a slider for lightness: the user’s intent when adjusting this slider is potentially ambiguous: how should the software deal with out-of-gamut colors? Or conversely, If the user has selected as colorful as possible a dark purple {{nobr|{{colorsample2|#42007F}},}} and then shifts the lightness slider upward, what should be done: would the user prefer to see a lighter purple still as colorful as possible for the given hue and lightness {{nobr|{{colorsample2|#7700E5}},}} or a lighter purple of exactly the same chroma as the original color {{nobr|{{colorsample2|#7533B2}}?}}<ref>Joblove and Greenberg 1978.</ref> | |||
| }} for every combination of hue and lightness or value.]] | |||
| When encoding colors in a hue/lightness/chroma or hue/value/chroma model (using the definitions from the previous two sections), not all combinations of lightness (or value) and chroma are meaningful: that is, half of the colors denotable using {{nobr|''H'' ∈ }}, and {{nobr|''V'' ∈ }} fall outside the RGB gamut (the gray parts of the slices in figure 14). The creators of these models considered this a problem for some uses. For example, in a color selection interface with two of the dimensions in a rectangle and the third on a slider, half of that rectangle is made of unused space. Now imagine we have a slider for lightness: the user's intent when adjusting this slider is potentially ambiguous: how should the software deal with out-of-gamut colors? Or conversely, If the user has selected as colorful as possible a dark purple {{nobr|{{colorsample2|#42007F}},}} and then shifts the lightness slider upward, what should be done: would the user prefer to see a lighter purple still as colorful as possible for the given hue and lightness {{nobr|{{colorsample2|#7700E5}},}} or a lighter purple of exactly the same chroma as the original color {{nobr|{{colorsample2|#7533B2}}?}}<ref name=Joblove/> | |||
| :<math>\begin{align} | |||
| S_{HSV} &= | |||
| \begin{cases} | |||
| 0, &\mbox{if } C = 0 \\ | |||
| \frac{C}{V}, &\mbox{otherwise} | |||
| \end{cases} \\ | |||
| S_{HSL} &= | |||
| \begin{cases} | |||
| 0, &\mbox{if } C = 0 \\ | |||
| \frac{C}{2L}, &\mbox{if } L \leq \frac{1}{2} \\ | |||
| \frac{C}{2-2L}, &\mbox{if } L > \frac{1}{2} | |||
| \end{cases} | |||
| \end{align}</math> | |||
| To solve problems such as these, the HSL and HSV models scale the chroma so that it always fits into the range {{nobr|}} for every combination of hue and lightness or value, calling the new attribute ''saturation'' in both cases (fig. 14). To calculate either, simply divide the chroma by the maximum chroma for that value or lightness. | |||
| ] | |||
| : <math>S_V = \begin{cases} | |||
| The HSI model commonly used for computer vision, which takes ''H''<sub>2</sub> as a hue dimension and the component average ''I'' (“intensity”) as a lightness dimension, does not attempt to “fill” a cylinder by its definition of saturation. Instead of presenting color choice or modification interfaces to end users, the goal of HSI is to facilitate separation of shapes in an image. Saturation is therefore defined in line with the psychometric definition: chroma relative to lightness ({{nobr|fig. 14}}). Specifically:<ref>Cheng et al. 2001.<br>Also see the ] section of this article.</ref> | |||
| 0, &\text{if } V = 0 \\ | |||
| \frac{C}{V}, &\text{otherwise} | |||
| \end{cases}</math> | |||
| :<math>S_L = \begin{cases} | |||
| 0, &\text{if } L = 1 \text{ or } L = 0 \\ | |||
| \frac{C}{1 - |2L - 1|}, &\text{otherwise} | |||
| \end{cases}</math> | |||
| ] | |||
| :<math> | |||
| S_{HSI} = | |||
| \begin{cases} | |||
| 0, &\mbox{if } C=0 \\ | |||
| 1 - \frac{m}{I}, &\mbox{otherwise} | |||
| \end{cases} | |||
| </math> | |||
| The HSI model commonly used for computer vision, which takes ''H''<sub>2</sub> as a hue dimension and the component average ''I'' ("intensity") as a lightness dimension, does not attempt to "fill" a cylinder by its definition of saturation. Instead of presenting color choice or modification interfaces to end users, the goal of HSI is to facilitate separation of shapes in an image. Saturation is therefore defined in line with the psychometric definition: chroma relative to lightness ({{nobr|fig. 15}}). See the ] section of this article.<ref name=Cheng>]</ref> | |||
| Using the same name for these three different definitions of saturation leads to some confusion, as the three attributes describe substantially different color relationships; in HSV and HSI, the term roughly matches the psychometric definition, of a the chroma of a color relative to its own lightness, but in HSL it does not come close. Even worse, the word ''saturation'' is also often used for one of the measurements we call chroma above (''C'' or ''C''<sub>2</sub>). | |||
| : <math>S_I = \begin{cases} | |||
| {{clear}} | |||
| 0, &\text{if } I = 0 \\ | |||
| 1 - \frac{m}{I}, &\text{otherwise} | |||
| \end{cases}</math> | |||
| Using the same name for these three different definitions of saturation leads to some confusion, as the three attributes describe substantially different color relationships; in HSV and HSI, the term roughly matches the psychometric definition, of a chroma of a color relative to its own lightness, but in HSL it does not come close. Even worse, the word ''saturation'' is also often used for one of the measurements we call chroma above (''C'' or ''C''<sub>2</sub>). | |||
| ===Examples=== | |||
| All parameter values shown below are given as values in the ] {{nobr|}}, except those for ''H'' and ''H''<sub>2</sub>, which are in the interval {{nobr|[0°, 360°)}}.{{refn|group=upper-alpha |The first nine colors in this table were chosen by hand, and the last ten colors were chosen at random.}} | |||
| {| class="wikitable" style="text-align:right;" cellpadding="6" | |||
| |- style="text-align:center;vertical-align:baseline;" | |||
| !Color | |||
| !style="min-width:3.2em;"|''R'' | |||
| !style="min-width:3.2em;"|''G'' | |||
| !style="min-width:3.2em;"|''B'' | |||
| !style="min-width:3.2em;"|''H'' | |||
| !style="min-width:3.2em;"|''H''<sub>2</sub> | |||
| !style="min-width:3.2em;"|''C'' | |||
| !style="min-width:3.2em;"|''C''<sub>2</sub> | |||
| !style="min-width:3.2em;"|''V'' | |||
| !style="min-width:3.2em;"|''L'' | |||
| !style="min-width:3.2em;"|''I'' | |||
| !style="min-width:3.2em;"|''{{prime|Y}}''<sub>601</sub> | |||
| !style="min-width:3.2em;"|''S''<sub>''HSV''</sub> | |||
| !style="min-width:3.2em;"|''S''<sub>''HSL''</sub> | |||
| !style="min-width:3.2em;"|''S''<sub>''HSI''</sub> | |||
| |- | |||
| |style="background-color:#FFFFFF; color:#FFFFFF"; title="#FFFFFF"; font-family=monospace, monospace|{{Ntsh|0}}#FFFFFF | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| |style="padding-right:.5em;"|n/a | |||
| |style="padding-right:.5em;"|n/a | |||
| | 0.000 | |||
| | 0.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| |- | |||
| |style="background-color:#808080; color:#808080"; title="#808080"; font-family=monospace, monospace|{{Ntsh|1}}#808080 | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.500 | |||
| |style="padding-right:.5em;"|n/a | |||
| |style="padding-right:.5em;"|n/a | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| |- | |||
| |style="background-color:#000000; color:#000000"; title="#000000"; font-family=monospace, monospace|{{Ntsh|2}}#000000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| |style="padding-right:.5em;"|n/a | |||
| |style="padding-right:.5em;"|n/a | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| |- | |||
| |style="background-color:#FF0000; color:#FF0000"; title="#FF0000"; font-family=monospace, monospace; font-family=monospace, monospace|{{Ntsh|3}}#FF0000 | |||
| | 1.000 | |||
| | 0.000 | |||
| | 0.000 | |||
| | {{Nts|0.0}}° | |||
| | {{Nts|0.0}}° | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 0.500 | |||
| | 0.333 | |||
| | 0.299 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| |- | |||
| |style="background-color:#BFBF00; color:#BFBF00"; title="#BFBF00"; font-family=monospace, monospace|{{Ntsh|4}}#BFBF00 | |||
| | 0.750 | |||
| | 0.750 | |||
| | 0.000 | |||
| | {{Nts|60.0}}° | |||
| | {{Nts|60.0}}° | |||
| | 0.750 | |||
| | 0.750 | |||
| | 0.750 | |||
| | 0.375 | |||
| | 0.500 | |||
| | 0.664 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| |- | |||
| |style="background-color:#008000; color:#008000"; title="#008000"; font-family=monospace, monospace|{{Ntsh|5}}#008000 | |||
| | 0.000 | |||
| | 0.500 | |||
| | 0.000 | |||
| | {{Nts|120.0}}° | |||
| | {{Nts|120.0}}° | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.250 | |||
| | 0.167 | |||
| | 0.293 | |||
| | 1.000 | |||
| | 1.000 | |||
| | 1.000 | |||
| |- | |||
| |style="background-color:#80FFFF; color:#80FFFF"; title="#80FFFF"; font-family=monospace, monospace|{{Ntsh|6}}#80FFFF | |||
| | 0.500 | |||
| | 1.000 | |||
| | 1.000 | |||
| | {{Nts|180.0}}° | |||
| | {{Nts|180.0}}° | |||
| | 0.500 | |||
| | 0.500 | |||
| | 1.000 | |||
| | 0.750 | |||
| | 0.833 | |||
| | 0.850 | |||
| | 0.500 | |||
| | 1.000 | |||
| | 0.400 | |||
| |- | |||
| |style="background-color:#8080FF; color:#8080FF"; title="#8080FF"; font-family=monospace, monospace|{{Ntsh|7}}#8080FF | |||
| | 0.500 | |||
| | 0.500 | |||
| | 1.000 | |||
| | {{Nts|240.0}}° | |||
| | {{Nts|240.0}}° | |||
| | 0.500 | |||
| | 0.500 | |||
| | 1.000 | |||
| | 0.750 | |||
| | 0.667 | |||
| | 0.557 | |||
| | 0.500 | |||
| | 1.000 | |||
| | 0.250 | |||
| |- | |||
| |style="background-color:#BF40BF; color:#BF40BF"; title="#BF40BF"; font-family=monospace, monospace|{{Ntsh|8}}#BF40BF | |||
| | 0.750 | |||
| | 0.250 | |||
| | 0.750 | |||
| | {{Nts|300.0}}° | |||
| | {{Nts|300.0}}° | |||
| | 0.500 | |||
| | 0.500 | |||
| | 0.750 | |||
| | 0.500 | |||
| | 0.583 | |||
| | 0.457 | |||
| | 0.667 | |||
| | 0.500 | |||
| | 0.571 | |||
| |- | |||
| |style="background-color:#A0A424; color:#A0A424"; title="#A0A424"; font-family=monospace, monospace|{{Ntsh|9}}#A0A424 | |||
| | 0.628 | |||
| | 0.643 | |||
| | 0.142 | |||
| | {{Nts|61.8}}° | |||
| | {{Nts|61.5}}° | |||
| | 0.501 | |||
| | 0.494 | |||
| | 0.643 | |||
| | 0.393 | |||
| | 0.471 | |||
| | 0.581 | |||
| | 0.779 | |||
| | 0.638 | |||
| | 0.699 | |||
| |- | |||
| |style="background-color:#411BEA; color:#411BEA"; title="#411BEA"; font-family=monospace, monospace|{{Ntsh|10}}#411BEA | |||
| | 0.255 | |||
| | 0.104 | |||
| | 0.918 | |||
| | {{Nts|251.1}}° | |||
| | {{Nts|250.0}}° | |||
| | 0.814 | |||
| | 0.750 | |||
| | 0.918 | |||
| | 0.511 | |||
| | 0.426 | |||
| | 0.242 | |||
| | 0.887 | |||
| | 0.832 | |||
| | 0.756 | |||
| |- | |||
| |style="background-color:#1EAC41; color:#1EAC41"; title="#1EAC41"; font-family=monospace, monospace|{{Ntsh|11}}#1EAC41 | |||
| | 0.116 | |||
| | 0.675 | |||
| | 0.255 | |||
| | {{Nts|134.9}}° | |||
| | {{Nts|133.8}}° | |||
| | 0.559 | |||
| | 0.504 | |||
| | 0.675 | |||
| | 0.396 | |||
| | 0.349 | |||
| | 0.460 | |||
| | 0.828 | |||
| | 0.707 | |||
| | 0.667 | |||
| |- | |||
| |style="background-color:#F0C80E; color:#F0C80E"; title="#F0C80E"; font-family=monospace, monospace|{{Ntsh|12}}#F0C80E | |||
| | 0.941 | |||
| | 0.785 | |||
| | 0.053 | |||
| | {{Nts|49.5}}° | |||
| | {{Nts|50.5}}° | |||
| | 0.888 | |||
| | 0.821 | |||
| | 0.941 | |||
| | 0.497 | |||
| | 0.593 | |||
| | 0.748 | |||
| | 0.944 | |||
| | 0.893 | |||
| | 0.911 | |||
| |- | |||
| |style="background-color:#B430E5; color:#B430E5"; title="#B430E5"; font-family=monospace, monospace|{{Ntsh|13}}#B430E5 | |||
| | 0.704 | |||
| | 0.187 | |||
| | 0.897 | |||
| | {{Nts|283.7}}° | |||
| | {{Nts|284.8}}° | |||
| | 0.710 | |||
| | 0.636 | |||
| | 0.897 | |||
| | 0.542 | |||
| | 0.596 | |||
| | 0.423 | |||
| | 0.792 | |||
| | 0.775 | |||
| | 0.686 | |||
| |- | |||
| |style="background-color:#ED7651; color:#ED7651"; title="#ED7651"; font-family=monospace, monospace|{{Ntsh|14}}#ED7651 | |||
| | 0.931 | |||
| | 0.463 | |||
| | 0.316 | |||
| | {{Nts|14.3}}° | |||
| | {{Nts|13.2}}° | |||
| | 0.615 | |||
| | 0.556 | |||
| | 0.931 | |||
| | 0.624 | |||
| | 0.570 | |||
| | 0.586 | |||
| | 0.661 | |||
| | 0.817 | |||
| | 0.446 | |||
| |- | |||
| |style="background-color:#FEF888; color:#FEF888"; title="#FEF888"; font-family=monospace, monospace|{{Ntsh|15}}#FEF888 | |||
| | 0.998 | |||
| | 0.974 | |||
| | 0.532 | |||
| | {{Nts|56.9}}° | |||
| | {{Nts|57.4}}° | |||
| | 0.466 | |||
| | 0.454 | |||
| | 0.998 | |||
| | 0.765 | |||
| | 0.835 | |||
| | 0.931 | |||
| | 0.467 | |||
| | 0.991 | |||
| | 0.363 | |||
| |- | |||
| |style="background-color:#19CB97; color:#19CB97"; title="#19CB97"; font-family=monospace, monospace|{{Ntsh|16}}#19CB97 | |||
| | 0.099 | |||
| | 0.795 | |||
| | 0.591 | |||
| | {{Nts|162.4}}° | |||
| | {{Nts|163.4}}° | |||
| | 0.696 | |||
| | 0.620 | |||
| | 0.795 | |||
| | 0.447 | |||
| | 0.495 | |||
| | 0.564 | |||
| | 0.875 | |||
| | 0.779 | |||
| | 0.800 | |||
| |- | |||
| |style="background-color:#362698; color:#362698"; title="#362698"; font-family=monospace, monospace|{{Ntsh|17}}#362698 | |||
| | 0.211 | |||
| | 0.149 | |||
| | 0.597 | |||
| | {{Nts|248.3}}° | |||
| | {{Nts|247.3}}° | |||
| | 0.448 | |||
| | 0.420 | |||
| | 0.597 | |||
| | 0.373 | |||
| | 0.319 | |||
| | 0.219 | |||
| | 0.750 | |||
| | 0.601 | |||
| | 0.533 | |||
| |- | |||
| |style="background-color:#7E7EB8; color:#7E7EB8"; title="#7E7EB8"; font-family=monospace, monospace|{{Ntsh|18}}#7E7EB8 | |||
| | 0.495 | |||
| | 0.493 | |||
| | 0.721 | |||
| | {{Nts|240.5}}° | |||
| | {{Nts|240.4}}° | |||
| | 0.228 | |||
| | 0.227 | |||
| | 0.721 | |||
| | 0.607 | |||
| | 0.570 | |||
| | 0.520 | |||
| | 0.316 | |||
| | 0.290 | |||
| | 0.135 | |||
| |} | |||
| ==Use in end-user software== | |||
| === Examples === | |||
| {{see also|Color picker|Image editing}} | |||
| All parameter values shown below are in the interval {{nobr|}}, except those for ''H'' and ''H''<sub>2</sub> which are in the interval {{nobr|[0°, 360°)}}.<ref>The first nine colors in this table were chosen by hand, and the last ten colors were chosen at random.</ref> | |||
| [[File:hsl-hsv-colorpickers.svg|thumb|right|300px|Fig 16a–g. By the 1990s, HSL and HSV color selection tools were ubiquitous. The screenshots above are taken from: {{ordered list | list-style-type = lower-alpha | |||
| {{Hsl-hsv-examples}} | |||
| | SGI ] 5, {{Circa|1995}}; | |||
| | ], {{Circa|1990}}; | |||
| | IBM ] 3, {{Circa|1994}}; | |||
| | Apple Macintosh ], {{Circa|1996}}; | |||
| | Fractal Design ], {{Circa|1993}}; | |||
| | Microsoft ], {{Circa|1992}}; | |||
| | ], {{Circa|1995}}. | |||
| }} These are undoubtedly based on earlier examples, stretching back to PARC and NYIT in the mid-1970s.{{refn|group=upper-alpha |See ]. Many of these screenshots were taken from the , and the rest were gathered from image search results.}}]] | |||
| The original purpose of HSL and HSV and similar models, and their most common current application, is in ]. At their simplest, some such color pickers provide three sliders, one for each attribute. Most, however, show a two-dimensional slice through the model, along with a slider controlling which particular slice is shown. The latter type of GUI exhibits great variety, because of the choice of cylinders, hexagonal prisms, or cones/bicones that the models suggest (see the diagram near the ]). Several color choosers from the 1990s are shown to the right, most of which have remained nearly unchanged in the intervening time: today, nearly every computer color chooser uses HSL or HSV, at least as an option. Some more sophisticated variants are designed for choosing whole sets of colors, basing their suggestions of compatible colors on the HSL or HSV relationships between them.{{refn|group=upper-alpha |For instance, a tool in ] CS4, and Adobe's related web tool, ], both allow users to define color schemes based on HSV relationships, but with a hue circle modified to better match the ] used traditionally by painters. The web tools , , and all pick color schemes with reference to HSL or HSV.}} | |||
| == Use in end-user software == | |||
| ] 5, ca. 1995; (b) Adobe ], ca. 1990; (c) IBM ] 3, ca. 1994; (d) Apple Macintosh ], ca. 1996; (e) Fractal Design ], ca. 1993; (f) Microsoft ], ca. 1992; (g) ], ca. 1995. These are undoubtedly based on earlier examples, stretching back to PARC and NYIT in the mid-1970s; (h) ]’s HSV-based color modifier; (i) ]’s video color adjustment tool, based on HSL or a similar model; (j) the hue/saturation tool in ] 2.5, ca. 1992.<ref>See Smith 1978. Many of these screenshots were taken from the , and the rest were gathered from image search results.</ref>]] | |||
| {{also|Color tool|Image editing}} | |||
| The original purpose of HSL and HSV and similar models, and their most common current application, is in ]. At their simplest, some such color pickers provide three sliders, one for each attribute. Most, however, show a two-dimensional slice through the model, along with a slider controlling which particular slice is shown. The latter type of GUI exhibits great variety, because of the choice of cylinders, hexagonal prisms, or cones/bicones that the models suggest (see the diagram near the ]). Several color choosers from the 1990s are shown to the right, most of which have remained nearly unchanged in the intervening time: today, nearly every computer color chooser uses HSL or HSV, at least as an option. Some more sophisticated variants are designed for choosing whole sets of colors, basing their suggestions of compatible colors on the HSL or HSV relationships between them.<ref>For instance, a tool in ] CS4, and Adobe’s related web tool, ], both allow users to define color schemes based on HSV relationships, but with a hue circle modified to better match the ] used traditionally by painters. The web tools , , and all pick color schemes with reference to HSL or HSV.</ref> | |||
| Most web applications needing color selection also base their tools on HSL or HSV, and pre-packaged open source color choosers exist for most major web front-end ]. The ] specification allows web authors to specify colors for their pages directly with HSL coordinates. |
Most web applications needing color selection also base their tools on HSL or HSV, and pre-packaged open source color choosers exist for most major web front-end ]. The ] specification allows web authors to specify colors for their pages directly with HSL coordinates.{{refn|group=upper-alpha |Try a web search for "'''' color picker" for examples for a given framework, or "] color picker" for general results.}}<ref>Tantek Çelik, Chris Lilley, and L. David Baron (July 2008). .</ref> | ||
| HSL and HSV are sometimes used to define gradients for ], as in maps or medical images. For example, the popular ] program ] historically applied customizable HSV-based gradients to numerical geographical data.<!-- Several studies have been done on color scheme choices for such data display, and the use of HSL- and HSV-based schemes has |
HSL and HSV are sometimes used to define gradients for ], as in maps or medical images. For example, the popular ] program ] historically applied customizable HSV-based gradients to numerical geographical data.<!-- Several studies have been done on color scheme choices for such data display, and the use of HSL- and HSV-based schemes has -->{{refn|group=upper-alpha |ArcGIS calls its map-symbol gradients "color ramps". Current versions of ArcGIS can use CIELAB instead for defining them.<ref>{{cite web |date=January 2008 |url=http://webhelp.esri.com/arcgisdesktop/9.2/index.cfm?TopicName=Working_with_color_ramps |title=Working with color ramps |publisher=] |access-date=August 30, 2017}}</ref>}} | ||
| {| class="wikitable" style="clear:right; float:right; margin:0.8em 0 0 1.0em;" | |||
| ] software also commonly includes tools for adjusting colors with reference to HSL or HSV coordinates, or to coordinates in a model based on the “intensity” or luma ]. In particular, tools with a pair of “hue” and “saturation” sliders are commonplace, dating to at least the late-1980s, but various more complicated color tools have also been implemented. For instance, the ] image viewer and color editor ] allowed six user-definable hue (''H'') ranges to be rotated and resized, included a ]-like control for saturation (''S''<sub>''HSV''</sub>), and a ]-like interface for controlling value (''V'') – see the image to the left. The image editor ] includes a “color correction” tool which affords complex remapping of points in a hue/saturation plane relative to either HSL or HSV space.<ref>For instance, the first version of Photoshop had an HSL-based tool; see in the GUIdebook for screenshots.<br>John Bradley (1994). ''XV 3.10a Manual''. <br>Kiril Sinkel (January 2010). . Digital Light & Color.</ref> | |||
| | <!--Deleted image removed: rowspan="2"--> border="0" | ]<div style="width:90px; font-size: smaller;" class="thumbcaption">Fig. 17. ]'s HSV-based color modifier.</div> | |||
| | border="0" | ]<div style="width:200px; font-size: smaller;" class="thumbcaption">Fig. 18. The hue/saturation tool in ] 2.5, ca. 1992.</div> | |||
| <!--Deleted image removed:|- | |||
| | border="0" | Deleted image removed: ] <div style="width:200px; font-size: smaller;" class="thumbcaption">Fig. 19. ]'s video color adjustment tool, based on HSL or a similar model.</div>--> | |||
| |} | |||
| ] software also commonly includes tools for adjusting colors with reference to HSL or HSV coordinates, or to coordinates in a model based on the "intensity" or luma ]. In particular, tools with a pair of "hue" and "saturation" sliders are commonplace, dating to at least the late-1980s, but various more complicated color tools have also been implemented. For instance, the ] image viewer and color editor ] allowed six user-definable hue (''H'') ranges to be rotated and resized, included a ]-like control for saturation (''S''<sub>''HSV''</sub>), and a ]-like interface for controlling value (''V'') – see fig. 17. The image editor ] includes a "color correction" tool which affords complex remapping of points in a hue/saturation plane relative to either HSL or HSV space.{{refn|group=upper-alpha |For instance, the first version of Photoshop had an HSL-based tool; see in the GUIdebook for screenshots.<ref>{{cite web|first1=John |last1=Bradley |date=1994 |url=http://www.trilon.com/xv/manual/xv-3.10a/color-editor-2.html |title=The HSV Modification Tools |website=John's World of XV and Other Cool Stuff}}</ref><ref>{{cite web|first1=Kiril |last1=Sinkel |date=January 2010 |url=http://www.dl-c.com/Temp/downloads/PW%20Doc/PW70.pdf |title=User Guide for Picture Window and Picture Window Pro Digital Light & Color |archive-url=https://web.archive.org/web/20140512231703/http://www.dl-c.com/Temp/downloads/PW%20Doc/PW70.pdf |archive-date=2014-05-12}}</ref>}} | |||
| ] also use these models. For example, both ] and ] include color tools based on HSL or a similar geometry for use adjusting the color in video. With the Avid tool |
] also use these models. For example, both ] and ] include color tools based on HSL or a similar geometry for use adjusting the color in video. With the Avid tool, users pick a vector by clicking a point within the hue/saturation circle to shift all the colors at some lightness level (shadows, mid-tones, highlights) by that vector. | ||
| Since version 4.0, Adobe |
Since version 4.0, Adobe Photoshop's "Luminosity", "Hue", "Saturation", and "Color" ] composite layers using a luma/chroma/hue color geometry. These have been copied widely, but several imitators use the HSL (e.g. ], ]) or HSV geometries instead.{{refn|group=upper-alpha |Photoshop's documentation explains that, e.g., "Luminosity: Creates a result color with the hue and saturation of the base color and the luminance of the blend color."<ref>{{cite web |url=https://helpx.adobe.com/photoshop/using/blending-modes.html |title=Blending Modes |work=Photoshop User Guide |date=February 15, 2017 |publisher=Adobe Systems Incorporated}}</ref>}}<!-- could use a ref about photoimpact, PSP, GIMP-->{{refn|group=upper-alpha |The HSL-style mode (with a Rec. 601 Luminosity) are also standardized in ] from a documentation contributed by Adobe and Canon.<ref>{{cite web |title=Compositing and Blending Level 1 |url=https://www.w3.org/TR/compositing-1 |website=www.w3.org}}</ref> GIMP 2.10 has switched to ] from its older HSV geometry.<ref>{{cite web |title=GIMP's LCH Blend Modes |url=https://ninedegreesbelow.com/photography/gimp-lch-blend-modes.html |website=Nine Degrees Below}}</ref>}} | ||
| {{clear |
{{clear left}} | ||
| == |
==Use in image analysis== | ||
| {{also|Computer vision|Image analysis}} | {{see also|Computer vision|Image analysis}} | ||
| HSL, HSV, HSI, or related models are often used in ] and ] for ] or ]. The applications of such tools include object detection, for instance in ]; ], for instance of ], ], or ]; ]; and ].<ref |
HSL, HSV, HSI, or related models are often used in ] and ] for ] or ]. The applications of such tools include object detection, for instance in ]; ], for instance of ], ], or ]; ]; and ].<ref name=Cheng/> | ||
| For the most part, computer vision algorithms used on color images are |
For the most part, computer vision algorithms used on color images are straightforward extensions to algorithms designed for ] images, for instance ] or ] of pixel colors, or ] ]. At the simplest, each color component is separately passed through the same algorithm. It is important, therefore, that the ] of interest can be distinguished in the color dimensions used. Because the ''R'', ''G'', and ''B'' components of an object's color in a digital image are all correlated with the amount of light hitting the object, and therefore with each other, image descriptions in terms of those components make object discrimination difficult. Descriptions in terms of hue/lightness/chroma or hue/lightness/saturation are often more relevant.<ref name=Cheng/> | ||
| Starting in the late 1970s, transformations like HSV or HSI were used as a compromise between effectiveness for segmentation and computational complexity. They can be thought of as similar in approach and intent to the neural processing used by human color vision, without agreeing in particulars: if the goal is object detection, roughly separating hue, lightness, and chroma or saturation is effective, but there is no particular reason to strictly mimic human color response. John |
Starting in the late 1970s, transformations like HSV or HSI were used as a compromise between effectiveness for segmentation and computational complexity. They can be thought of as similar in approach and intent to the neural processing used by human color vision, without agreeing in particulars: if the goal is object detection, roughly separating hue, lightness, and chroma or saturation is effective, but there is no particular reason to strictly mimic human color response. John Kender's 1976 master's thesis proposed the HSI model. Ohta et al. (1980) instead used a model made up of dimensions similar to those we have called ''I'', ''α'', and ''β''. In recent years, such models have continued to see wide use, as their performance compares favorably with more complex models, and their computational simplicity remains compelling.{{refn|group=upper-alpha |The Ohta et al. model has parameters {{nobr|1=''I''<sub>1</sub> = (''R'' + ''G'' + ''B'')/3}}, {{nobr|1=''I''<sub>2</sub> = (''R'' − ''B'')/2}}, {{nobr|1=''I''<sub>3</sub> = (2''G'' − ''R'' − ''B'')/4}}. ''I''<sub>1</sub> is the same as our ''I'', and ''I''<sub>2</sub> and ''I''<sub>3</sub> are similar to our ''β'' and ''α'', respectively, except that (a) where ''α'' points in the direction of ''R'' in the "chromaticity plane", ''I''<sub>3</sub> points in the direction of ''G'', and (b) the parameters have a different linear scaling which avoids the {{radic|3}} of our ''β''.}}<ref name=Cheng/><ref>John Kender (1976). "Saturation, hue and normalized color". Carnegie Mellon University, Computer Science Dept. Pittsburgh, PA.</ref><ref>{{cite journal|author1=Yu-Ichi Ohta |author2=Takeo Kanade |author3=Toshiyuki Sakai |doi=10.1016/0146-664X(80)90047-7|title=Color information for region segmentation|year=1980|journal=Computer Graphics and Image Processing|volume=13|issue=3|pages=222}}</ref><ref>{{cite journal|author1=Ffrank Perez |author2=Christof Koch |doi=10.1007/BF01420983|title=Toward color image segmentation in analog VLSI: Algorithm and hardware|year=1994|journal=International Journal of Computer Vision|volume=12|pages=17–42|s2cid=6140819 |url=https://authors.library.caltech.edu/40488/1/370338.pdf}}</ref> | ||
| <!-- | <!-- | ||
| Demarty, C.-H., Beucher, S., 1998. Color segmentation algorithm using an HLS transformation. In: Proceedings of the International Symposium on Mathematical Morphology (ISMM ’98). {{nobr|pp. 231–238}}. | Demarty, C.-H., Beucher, S., 1998. Color segmentation algorithm using an HLS transformation. In: Proceedings of the International Symposium on Mathematical Morphology (ISMM ’98). {{nobr|pp. 231–238}}. | ||
| --> | --> | ||
| == |
==Disadvantages== | ||
| {{multiple image | |||
| {{double image|right|srgb-in-cielab.png|197|adobergb-in-cielab.png|197|Fig 19a. The ] gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced according to their hue angle. They are also of unequal length. In addition, each of the three primaries have different L* values.|b. The ] gamut mapped in CIELAB space. Notice that the gamut (roughly, the area of the plot) of the Adobe RGB space is different from sRGB. As a result, the two spaces will also have different HSL and HSV representations.}} | |||
| | align = right | |||
| While HSL, HSV, and related spaces serve well enough to, for instance, choose a single color, they ignore much of the complexity of color appearance. Essentially, they trade off perceptual relevance for computation speed, from a time in computing history (high-end 1970s graphics workstations, or mid-1990s consumer desktops) when more sophisticated models would have been too computationally expensive.<ref>Most of the disadvantages below are listed in Poynton 1997, though as mere statements, without examples.</ref> | |||
| | image1 = srgb-in-cielab.png | |||
| | width1 = 197 | |||
| | alt1 = | |||
| | caption1 = Fig 20a. The ] gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced by ], and are of unequal length. The primaries also have different ''L''* values. | |||
| | image2 = adobergb-in-cielab.png | |||
| | width2 = 197 | |||
| | alt2 = | |||
| | caption2 = Fig 20b. The ] gamut mapped in CIELAB space. Also notice that these two RGB spaces have different gamuts, and thus will have different HSL and HSV representations. | |||
| | footer = | |||
| }} | |||
| While HSL, HSV, and related spaces serve well enough to, for instance, choose a single color, they ignore much of the complexity of color appearance. Essentially, they trade off perceptual relevance for computation speed, from a time in computing history (high-end 1970s graphics workstations, or mid-1990s consumer desktops) when more sophisticated models would have been too computationally expensive.{{refn|group=upper-alpha |Most of the disadvantages below are listed in ], though as mere statements, without examples.}} | |||
| HSL and HSV are simple transformations of RGB which preserve symmetries in the RGB cube unrelated to human perception, such |
HSL and HSV are simple transformations of RGB which preserve symmetries in the RGB cube unrelated to human perception, such that its ''R'', ''G'', and ''B'' corners are equidistant from the neutral axis, and equally spaced around it. If we plot the RGB gamut in a more perceptually-uniform space, such as ] (see ]), it becomes immediately clear that the red, green, and blue primaries do not have the same lightness or chroma, or evenly spaced hues. Furthermore, different RGB displays use different primaries, and so have different gamuts. Because HSL and HSV are defined purely with reference to some RGB space, they are not ]s: to specify a color precisely requires reporting not only HSL or HSV values, but also the characteristics of the RGB space they are based on, including the ] in use. | ||
| If we take an image and extract the hue, saturation, and lightness or value components, and then compare these to the components of the same name as defined by color scientists, we can quickly see the difference, perceptually. For example, |
If we take an image and extract the hue, saturation, and lightness or value components, and then compare these to the components of the same name as defined by color scientists, we can quickly see the difference, perceptually. For example, examine the following images of a fire breather ({{nobr|fig. 13}}). The original is in the sRGB colorspace. CIELAB ''L''* is a CIE-defined achromatic lightness quantity (dependent solely on the perceptually achromatic luminance ''Y'', but not the mixed-chromatic components ''X'' or ''Z'', of the CIEXYZ colorspace from which the sRGB colorspace itself is derived), and it is plain that this appears similar in perceptual lightness to the original color image. Luma is roughly similar, but differs somewhat at high chroma, where it deviates most from depending solely on the true achromatic luminance (''Y'', or equivalently ''L''*) and is influenced by the colorimetric chromaticity (''x,y'', or equivalently, ''a*,b*'' of CIELAB). HSL ''L'' and HSV ''V'', by contrast, diverge substantially from perceptual lightness. | ||
| {{clear}} | {{clear}} | ||
| {{triple image|center|Fire breathing 2 Luc Viatour.jpg|220|Fire-breather CIELAB L*.jpg|220|Fire-breather mean(R,G,B) I.jpg|220|Fig. 12a. Color photograph|b. CIELAB ''L''*|c. Component average: “intensity” ''I''|A full-color image shows a high-contrast and quite dramatic scene of a fire breather with a large orange-yellow flame extending from his lips. He wears dark but colorful orange-red clothing.|A grayscale image showing the CIELAB lightness component of the photograph appears to be a faithful rendering of the scene: it looks roughly like a black-and-white photograph taken on panchromatic film would look, with clear detail in the flame, which is much brighter than the man's outfit or the background.|A grayscale image showing the component average (HSI intensity) of the photograph is much a less convincing facsimile of the color photograph, with reduced contrast, especially with its flame darker than in the original.}} | |||
| {{triple image|center|Fire-breather HSV V.jpg|220|Fire-breather HSL L.jpg|220|Fire-breather 601 Luma Y'.jpg|220|d. HSV value ''V''|e. HSL lightness ''L''|f. Rec. 601 luma {{nobr|''Y''′}}|A grayscale image showing the HSV value component of the photograph leaves the flame completely white (in photographer's parlance, “blown out”), and the man’s clothing much too bright.|A grayscale image showing the HSL lightness component of the photograph renders the flame, as approximately middle gray, and ruins the dramatic effect of the original by radically reducing its contrast.|A grayscale image showing the luma appears roughly similar to the CIELAB lightness image, but is a bit brighter in areas which were originally very colorful.}} | |||
| {{multiple image | |||
| | align = center | |||
| | image1 = Fire breathing 2 Luc Viatour.jpg | |||
| | width1 = 220 | |||
| | alt1 = A full-color image shows a high-contrast and quite dramatic scene of a fire breather with a large orange-yellow flame extending from his lips. He wears dark but colorful orange-red clothing. | |||
| | caption1 = Fig. 13a. Color photograph (sRGB colorspace). | |||
| | image2 = Fire-breather CIELAB L*.jpg | |||
| | width2 = 220 | |||
| | alt2 = A grayscale image showing the CIELAB lightness component of the photograph appears to be a faithful rendering of the scene: it looks roughly like a black-and-white photograph taken on panchromatic film would look, with clear detail in the flame, which is much brighter than the man's outfit or the background. | |||
| | caption2 = Fig. 13b. CIELAB ''L''* (further transformed back to sRGB for consistent display). | |||
| | image3 = Fire-breather 601 Luma Y'.jpg | |||
| | width3 = 220 | |||
| | alt3 = A grayscale image showing the luma appears roughly similar to the CIELAB lightness image, but is a bit brighter in areas which were originally very colorful. | |||
| | caption3 = Fig. 13c. Rec. 601 luma {{nobr|''Y'''}}. | |||
| | footer = | |||
| }} | |||
| {{multiple image | |||
| | align = center | |||
| | image1 = Fire-breather mean(R,G,B) I.jpg | |||
| | width1 = 220 | |||
| | alt1 = A grayscale image showing the component average (HSI intensity) of the photograph is much a less convincing facsimile of the color photograph, with reduced contrast, especially with its flame darker than in the original. | |||
| | caption1 = Fig. 13d. Component average: "intensity" ''I''. | |||
| | image2 = Fire-breather HSV V.jpg | |||
| | width2 = 220 | |||
| | alt2 = A grayscale image showing the HSV value component of the photograph leaves the flame completely white (in photographer's parlance, "blown out"), and the man's clothing much too bright. | |||
| | caption2 = Fig. 13e. HSV value ''V''. | |||
| | image3 = Fire-breather HSL L.jpg | |||
| | width3 = 220 | |||
| | alt3 = A grayscale image showing the HSL lightness component of the photograph renders the flame, as approximately middle gray, and ruins the dramatic effect of the original by radically reducing its contrast. | |||
| | caption3 = Fig. 13f. HSL lightness ''L''. | |||
| | footer = | |||
| }} | |||
| ] chroma plane, showing HSV's lack of uniformity in hue and saturation.]] | |||
| Though none of the dimensions in these spaces match their perceptual analogs, the ''value'' of HSV and the ''saturation'' of HSL are particular offenders. In HSV, the blue primary {{colorsample2|#0000FF}} and white {{colorsample2|#FFFFFF}} are held to have the same value, even though perceptually the blue primary has somewhere around 10% of the luminance of white (the exact fraction depends on the particular RGB primaries in use). In HSL, a mix of 100% red, 100% green, 90% blue – that is, a very light yellow {{colorsample2|#FFFFE5}} – is held to have the same saturation as the green primary {{nobr|{{colorsample2|#00FF00}},}} even though the former color has almost no chroma or saturation by the conventional psychometric definitions. Such perversities led Cynthia Brewer, expert in color scheme choices for maps and information displays, to tell the ]: | Though none of the dimensions in these spaces match their perceptual analogs, the ''value'' of HSV and the ''saturation'' of HSL are particular offenders. In HSV, the blue primary {{colorsample2|#0000FF}} and white {{colorsample2|#FFFFFF}} are held to have the same value, even though perceptually the blue primary has somewhere around 10% of the luminance of white (the exact fraction depends on the particular RGB primaries in use). In HSL, a mix of 100% red, 100% green, 90% blue – that is, a very light yellow {{colorsample2|#FFFFE5}} – is held to have the same saturation as the green primary {{nobr|{{colorsample2|#00FF00}},}} even though the former color has almost no chroma or saturation by the conventional psychometric definitions. Such perversities led Cynthia Brewer, expert in color scheme choices for maps and information displays, to tell the ]: | ||
| {{ |
{{quote|Computer science offers a few poorer cousins to these perceptual spaces that may also turn up in your software interface, such as HSV and HLS. They are easy mathematical transformations of RGB, and they seem to be perceptual systems because they make use of the hue–lightness/value–saturation terminology. But take a close look; don't be fooled. Perceptual color dimensions are poorly scaled by the color specifications that are provided in these and some other systems. For example, saturation and lightness are confounded, so a saturation scale may also contain a wide range of lightnesses (for example, it may progress from white to green which is a combination of both lightness and saturation). Likewise, hue and lightness are confounded so, for example, a saturated yellow and saturated blue may be designated as the same 'lightness' but have wide differences in perceived lightness. These flaws make the systems difficult to use to control the look of a color scheme in a systematic manner. If much tweaking is required to achieve the desired effect, the system offers little benefit over grappling with raw specifications in RGB or CMY.<ref>{{cite conference |url=http://www.personal.psu.edu/cab38/ColorSch/ASApaper.html |title=Color Use Guidelines for Data Representation |first=Cynthia A. |last=Brewer |date=1999 |book-title=Proceedings of the Section on Statistical Graphics |location=Alexandria, VA |publisher=American Statistical Association |pages=55–60 |access-date=2010-02-05 |archive-date=2009-08-07 |archive-url=https://web.archive.org/web/20090807105257/http://www.personal.psu.edu/cab38/ColorSch/ASApaper.html |url-status=dead }}</ref>}} | ||
| If these problems make HSL and HSV problematic for choosing colors or color schemes, they make them much worse for image adjustment. HSL and HSV, as Brewer mentioned, confound perceptual color-making attributes, so that changing any dimension results in non-uniform changes to all three perceptual dimensions, and distorts all of the color relationships in the image. For instance, rotating the hue of a pure dark blue {{colorsample2|#002BA6}} toward green {{colorsample2|#0087A6}} will also reduce its perceived chroma, and increase its perceived lightness (the latter is grayer and lighter), but the same hue rotation will have the opposite impact on lightness and chroma of a lighter bluish-green – {{colorsample2|#00D6AF}} to {{colorsample2|#00D639}} (the latter is more colorful and slightly darker). In the example below ({{nobr|fig. |
If these problems make HSL and HSV problematic for choosing colors or color schemes, they make them much worse for image adjustment. HSL and HSV, as Brewer mentioned, confound perceptual color-making attributes, so that changing any dimension results in non-uniform changes to all three perceptual dimensions, and distorts all of the color relationships in the image. For instance, rotating the hue of a pure dark blue {{colorsample2|#002BA6}} toward green {{colorsample2|#0087A6}} will also reduce its perceived chroma, and increase its perceived lightness (the latter is grayer and lighter), but the same hue rotation will have the opposite impact on lightness and chroma of a lighter bluish-green – {{colorsample2|#00D6AF}} to {{colorsample2|#00D639}} (the latter is more colorful and slightly darker). In the example below ({{nobr|fig. 21}}), the image (a) is the original photograph of a ]. In the image (b), we have rotated the hue (''H'') of each color by {{nowrap|−30°}}, while keeping HSV value and saturation or HSL lightness and saturation constant. In the image right (c), we make the same rotation to the HSL/HSV hue of each color, but then we force the CIELAB lightness (''L''*, a decent approximation of perceived lightness) to remain constant. Notice how the hue-shifted middle version without such a correction dramatically changes the perceived lightness relationships between colors in the image. In particular, the turtle's shell is much darker and has less contrast, and the background water is much lighter. Image (d) uses CIELAB to hue shift; the difference from (c) demonstrates the errors in hue and saturation. | ||
| {{clear}} | {{clear}} | ||
| {{triple image|center|Hawaii turtle 2.JPG|220|Hawaii-turtle hue shifted.jpg|220|Hawaii-turtle hue shifted with constant L*.jpg|220|Fig. 20a. Color photograph|b. HSL/HSV hue of each color shifted by {{nowrap|−30°}}|c. Hue shifted but CIELAB lightness (''L''*) kept as in the original}} | |||
| {{multiple image | |||
| Because hue is a circular quantity, represented numerically with a discontinuity at 360°, it is difficult to use in statistical computations or quantitative comparisons: analysis requires the use of ]. Furthermore, hue is defined piecewise, in 60° chunks, where the relationship of lightness, value, and chroma to ''R'', ''G'', and ''B'' depends on the hue chunk in question. This definition introduces discontinuities, corners which can plainly be seen in horizontal slices of HSL or HSV.<ref>Allan Hanbury (2003). . ''8th Computer Vision Winter Workshop''.<br>Circular statistics are described in the textbook:<br>Nicholas Fisher (1996). . Cambridge, England: Cambridge University Press.</ref> | |||
| | align = center | |||
| | image1 = Hawaii turtle 2.JPG | |||
| | width1 = 220 | |||
| | alt1 = | |||
| | caption1 = Fig. 21a. Color photograph. | |||
| | image2 = Hawaii-turtle hue shifted.jpg | |||
| | width2 = 220 | |||
| | alt2 = | |||
| | caption2 = Fig. 21b. HSL/HSV hue of each color shifted by {{nowrap|−30°}}. | |||
| | image3 = Hawaii-turtle hue shifted with constant L*.jpg | |||
| | width3 = 220 | |||
| | alt3 = | |||
| | caption3 = Fig. 21c. Hue shifted but CIELAB lightness (''L''*) kept as in the original. | |||
| | image4 = Hawaii turtle 2 hue shifted lch.JPG | |||
| | width4 = 220 | |||
| | alt4 = | |||
| | caption4 = Fig. 21d. Hue shifted in CIELch(ab) color space by {{nowrap|−30°}}. | |||
| | footer = | |||
| }} | |||
| Because hue is a circular quantity, represented numerically with a discontinuity at 360°, it is difficult to use in statistical computations or quantitative comparisons: analysis requires the use of ].<ref>{{cite book | first = Nicholas | last = Fisher | year = 1993 | url = https://archive.org/details/statisticalanaly0000fish_v6v2/ |url-access=limited | title = Statistical Analysis of Circular Dat | publisher = Cambridge University Press |doi=10.1017/CBO9780511564345 | isbn = 978-0-521-35018-1 }}</ref> Furthermore, hue is defined piecewise, in 60° chunks, where the relationship of lightness, value, and chroma to ''R'', ''G'', and ''B'' depends on the hue chunk in question. This definition introduces discontinuities, corners which can plainly be seen in horizontal slices of HSL or HSV.<ref>{{cite conference | first = Allan | last = Hanbury | year = 2003 | citeseerx = 10.1.1.4.1381 | title = Circular Statistics Applied to Colour Images | conference = 8th Computer Vision Winter Workshop}}</ref> | |||
| Charles Poynton, digital video expert, lists the above problems with HSL and HSV in his ''Color FAQ'', and concludes that: | Charles Poynton, digital video expert, lists the above problems with HSL and HSV in his ''Color FAQ'', and concludes that: | ||
| {{ |
{{quote|HSB and HLS were developed to specify numerical Hue, Saturation and Brightness (or Hue, Lightness and Saturation) in an age when users had to specify colors numerically. The usual formulations of HSB and HLS are flawed with respect to the properties of color vision. Now that users can choose colors visually, or choose colors related to other media (such as ]), or use perceptually-based systems like ] and ], HSB and HLS should be abandoned.<ref>]. </ref>}} | ||
| == |
==Other cylindrical-coordinate color models== | ||
| {{main|Color model#Cylindrical-coordinate color models|List of color spaces and their uses#Cylindrical transformations}} | |||
| {{multiple image | |||
| The creators of HSL and HSV were far from the first to imagine colors fitting into conic or spherical shapes, with neutrals running from black to white in a central axis, and hues corresponding to angles around that axis. Similar arrangements date back to the 18th century, and continue to be developed in the most modern and scientific models. | |||
| | align = right | |||
| | image1 = Runge Farbenkugel.jpg | |||
| | width1 = 197 | |||
| | alt1 = | |||
| | caption1 = Fig. 21. Runge’s ''Farbenkugel'', 1810. | |||
| | image2 = Munsell color sphere.png | |||
| | width2 = 197 | |||
| | alt2 = | |||
| | caption2 = Fig. 22. Munsell’s balanced color sphere, 1900, from ''A Color Notation'', 1905. | |||
| }} | |||
| {{also|Color solid}} | |||
| The creators of HSL and HSV were far from the first to imagine colors fitting into conic or spherical shapes, with neutrals running from black to white in a central axis, and hues corresponding to angles around that axis. Similar arrangements date back to the 18th century, and continue to be developed in the most modern and scientific models. A pair of the most influential older models are ]’s 1810 ''Farbenkugel'' (color sphere), and the early-20th-century ]. ] began with a spherical arrangement in his 1905 book ''A Color Notation'', but he wished to properly separate color-making attributes into separate dimensions, which he called ''hue'', ''value'', and ''chroma'', and after taking careful measurements of perceptual responses, he realized that no symmetrical shape would do, so he reorganized his system into a lumpy blob.<ref>] (1810). ''Die Farben-Kugel, oder Construction des Verhaeltnisses aller Farben zueinander''. Hamburg, Germany: Perthes.<br>] (1905). ''A Color Notation''. Boston, MA: ].<br>See also Fairchild (2005), and ] and its references.</ref> | |||
| ==Color conversion formulae== | |||
| Munsell’s system became extremely popular, the de facto reference for American color standards – used not only for specifying the color of paints and crayons, but also, e.g., electrical wire, beer, and soil color – because it was organized based on perceptual measurements, specified colors via an easily learned and systematic triple of numbers, because the color chips sold in the ''Munsell Book of Color'' covered a wide ] and remained stable over time (rather than fading), and because it was effectively marketed by ]. In the 1940s, the ] made extensive measurements, and adjusted the arrangement of Munsell colors, issuing a set of “renotations”. The trouble with the Munsell system for computer graphics applications is that its colors are not specified via any set of simple equations, but only via its foundational measurements: effectively a ]. Converting from {{nobr|RGB ↔ Munsell}} requires interpolating between that table’s entries, and is extremely computationally expensive in comparison with converting from {{nobr|RGB ↔ HSL}} or {{nobr|RGB ↔ HSV}} which only requires a few simple arithmetic operations.<ref>Fairchild 2005.<br>Edward Landa and Mark Fairchild (September–October 2005). . ''American Scientist'' '''93'''(5): 436<br>Dorothy Nickerson (1976). “History of the Munsell Color System”. ''Color Research and Application'' '''1''': 121–130.<br>Sidney Newhall, Dorothy Nickerson, and Deane Judd (1943). “Final Report of the O.S.A. Subcommittee on the Spacing of the Munsell Colors”. ''Journal of the Optical Society of America'' '''33'''(7): 385–418.</ref> | |||
| To convert from HSL or HSV to RGB, we essentially invert the steps listed ] (as before, {{math|1=''R'', ''G'', ''B'' ] ]]}}). First, we compute chroma, by multiplying saturation by the maximum chroma for a given lightness or value. Next, we find the point on one of the bottom three faces of the RGB cube which has the same hue and chroma as our color (and therefore projects onto the same point in the chromaticity plane). Finally, we add equal amounts of ''R'', ''G'', and ''B'' to reach the proper lightness or value.{{refn|group=upper-alpha |name=formulasources}} | |||
| === To RGB === | |||
| In ], a model quite similar to the hue defined above is used for describing colors of ] inks. In 1953, Frank Preucil developed two geometric arrangements of hue, the “Preucil hue circle” and the “Preucil hue hexagon”, analogous to our ''H'' and ''H''<sub>2</sub>, respectively, but defined relative to idealized cyan, yellow, and magenta ink colors. The ] of an ink indicates the difference in the “hue circle” between its color and the hue of the corresponding idealized ink color. The ''grayness'' of an ink is {{nobr|''m''/''M''}}, where ''m'' and ''M'' are the minimum and maximum among the amounts of idealized cyan, magenta, and yellow in a density measurement.<ref>Frank Preucil (1953). “Color Hue and Ink Transfer – Their Relation to Perfect Reproduction”. ''Proceedings of the 5th Annual Technical Meeting of TAGA''. {{nobr|pp. 102–110}}.<br>See also ].</ref> | |||
| ====HSL to RGB==== | |||
| Given a color with hue {{math|''H'' ∈ }}, and lightness {{math|''L'' ∈ }}, we first find chroma: | |||
| The Swedish ] (NCS), widely used in Europe, takes a similar approach to the Ostwald bicone ]. Because it attempts to fit color into a familiarly shaped solid based on “]” instead of photometric or psychological characteristics, it suffers from some of the same disadvantages as HSL and HSV: in particular, its lightness dimension differs from perceived lightness, because it forces colorful yellow, red, green, and blue into a plane.<ref>MacEvoy 2010.<br></ref> | |||
| : <math>C = (1 - \left\vert 2 L - 1 \right\vert) \times S_L</math> | |||
| Then we can find a point {{math|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value ''X'' for the second largest component of this color): | |||
| The ] (CIE) developed the ] for describing the colors of light spectra in 1931, but its goal was to match human visual ], rather than to be perceptually uniform, geometrically. In the 1960s and 70s, attempts were made to transform XYZ colors into a more relevant geometry, influenced by the Munsell system. These efforts culminated in the 1976 ] and ] models. The dimensions of these models – {{nobr|(''L''*, ''u''*, ''v''*)}} and {{nobr|(''L''*, ''a''*, ''b''*)}}, respectively – are cartesian, based on the ] theory of color, but both are also often described using polar coordinates – {{nobr|(''L''*, ''C''*<sub>''uv''</sub>, ''h''*<sub>''uv''</sub>)}} or {{nobr|(''L''*, ''C''*<sub>''ab''</sub>, ''h''*<sub>''ab''</sub>)}}, where ''L''* is lightness, ''C''* is chroma, and ''h''* is hue angle. Officially, both CIELAB and CIELUV were created for their ] metrics ∆''E''*<sub>''ab''</sub> and ∆''E''*<sub>''uv''</sub>, particularly for use defining color tolerances, but both have become widely used as color order systems and color appearance models, including in computer graphics and computer vision. For example, ] in ] ] is usually performed in CIELAB space, and Adobe Photoshop includes a CIELAB mode for editing images. CIELAB and CIELUV geometries are dramatically more perceptually relevant than RGB, HSL, HSV, or XYZ, but are not perfect, and in particular have trouble adapting to unusual lighting conditions.<ref>Fairchild 2005.<br>Kuehni 2003.<br>Robert Hunt (2004). ''The Reproduction of Colour''. 6th ed. MN: Voyageur Press. ISBN 0-86343-368-5.<br>MacEvoy 2010. <br>Adobe (January 2007). . Technical Note 310838.<br>Steven K. Shevell (2003) ''The Science of Color''. 2nd ed. Elsevier Science & Technology. ISBN 0-444-51251-9. <br>See also ], ], ], ], and their references.</ref> | |||
| : <math>H^\prime = \frac{H}{60^\circ}</math> | |||
| : <math>X = C \times (1 - |H^\prime \;\bmod 2 - 1|)</math> | |||
| In the above equation, the notation <math>H^\prime \;\bmod 2</math> refers to the remainder of the ] of <math>H^\prime</math> by 2. <math>H^\prime</math> is not necessarily an integer. | |||
| : <math>(R_1, G_1, B_1) = \begin{cases} | |||
| (C, X, 0) &\text{if } 0 \leq H^\prime < 1 \\ | |||
| (X, C, 0) &\text{if } 1 \leq H^\prime < 2 \\ | |||
| (0, C, X) &\text{if } 2 \leq H^\prime < 3 \\ | |||
| (0, X, C) &\text{if } 3 \leq H^\prime < 4 \\ | |||
| (X, 0, C) &\text{if } 4 \leq H^\prime < 5 \\ | |||
| (C, 0, X) &\text{if } 5 \leq H^\prime < 6 | |||
| \end{cases}</math> | |||
| When <math>H^\prime</math> is an integer, the "neighbouring" formula would yield the same result, as <math>X = 0</math> or <math>X = C</math>, as appropriate. | |||
| The CIE’s most recent model, ] (CAM stands for “color appearance model”), is more theoretically sophisticated and computationally complex than earlier models. Its aims are to fix several of the problems with models such as CIELAB and CIELUV, and to explain not only responses in carefully controlled experimental environments, but also to model the color appearance of real-world scenes. Its dimensions ''J'' (lightness), ''C'' (chroma), and ''h'' (hue) define a polar-coordinate geometry.<ref>Fairchild 2005.<br>MacEvoy 2010</ref> | |||
| <!-- TODO: add some pictures after the top pair? --> | |||
| Finally, we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match lightness: | |||
| == Converting to RGB == | |||
| To convert from HSL or HSV to RGB, we essentially invert the steps listed ]. First, we compute chroma, by multiplying saturation by the maximum chroma for a given lightness or value. Next, we find the point on one of the bottom three faces of the RGB cube which has the same hue and chroma as our color (and therefore projects onto the same point in the chromaticity plane). Finally, we add equal amounts of ''R'', ''G'', and ''B'' to reach the proper lightness or value. | |||
| : <math>m = L-\frac{C}{2}</math> | |||
| === From HSV === | |||
| : <math>(R,G,B) = (R_{1}+m,G_{1}+m,B_{1}+m)</math> | |||
| ] | |||
| Given a color with hue {{nobr|''H'' ∈ }}, and value {{nobr|''V'' ∈ }}, we first find chroma: | |||
| ===== HSL to RGB alternative ===== | |||
| :<math>C = V \times S_{HSV}\,\!</math> | |||
| The polygonal piecewise functions can be somewhat simplified by clever use of minimum and maximum values as well as the remainder operation. | |||
| Then we can find a point {{nobr|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value ''X'' for the second largest component of this color): | |||
| Given a color with hue <math>H \in </math>, saturation <math>S=S_L \in </math>, and lightness <math>L \in </math>, we first define the function: | |||
| :<math>\begin{align} | |||
| : <math>f(n) = L - a \max(-1, \min(k-3,9-k,1))</math> | |||
| H^\prime &= \frac{H}{60^\circ} \\ | |||
| X &= C (1 - |H^\prime \;\bmod 2 - 1|) | |||
| where <math>k,n \in \mathbb R_{\geq 0}</math> and: | |||
| \end{align}</math> | |||
| :<math> | |||
| : <math>k = (n+\frac{H}{30^\circ}) \bmod 12</math> | |||
| (R_1, G_1, B_1) = | |||
| : <math>a = S_L \min(L,1-L)</math> | |||
| \begin{cases} | |||
| (0, 0, 0) &\mbox{if } H \mbox{ is undefined} \\ | |||
| And output R,G,B values (from <math>^3</math>) are: | |||
| (C, X, 0) &\mbox{if } 0 \leq H^\prime < 1 \\ | |||
| (X, C, 0) &\mbox{if } 1 \leq H^\prime < 2 \\ | |||
| : <math>(R,G,B) = (f(0), f(8), f(4))</math> | |||
| (0, C, X) &\mbox{if } 2 \leq H^\prime < 3 \\ | |||
| (0, X, C) &\mbox{if } 3 \leq H^\prime < 4 \\ | |||
| The above alternative formulas allow for shorter implementations. In the above formulas the <math>a\bmod b</math> operation also returns the fractional part of the module e.g. <math> 7.4 \bmod 6 = 1.4</math>, and <math>k \in [0,12)</math>. | |||
| (X, 0, C) &\mbox{if } 4 \leq H^\prime < 5 \\ | |||
| (C, 0, X) &\mbox{if } 5 \leq H^\prime < 6 | |||
| The base shape <math>T(k) = t(n,H) = \max(\min(k-3,9-k,1), -1)</math> is constructed as follows: <math>t_1 = \min(k-3,9-k)</math> is a "triangle" for which values greater or equal to −1 start from k=2 and end at k=10, and the highest point is at k=6. Then by <math>t_2 = \min(t_1,1) = \min(k-3,9-k,1)</math> we change values bigger than 1 to equal 1. Then by <math>t = \max(t_2,-1)</math> we change values less than −1 to equal −1. At this point, we get something similar to the red shape from fig. 24 after a vertical flip (where the maximum is 1 and the minimum is −1). The R,G,B functions of <math>H</math> use this shape transformed in the following way: modulo-shifted on <math>X</math> (by <math>n</math>) (differently for R,G,B) scaled on <math>Y</math> (by <math>-a</math>) and shifted on <math>Y</math> (by <math>L</math>). | |||
| \end{cases} | |||
| </math> | |||
| We observe the following shape properties (Fig. 24 can help to get an intuition about them): | |||
| : <math>t(n,H) = -t(n+6,H)</math> | |||
| : <math>\min\ (t(n,H), t(n+4,H), t(n+8,H)) = -1</math> | |||
| : <math>\max\ (t(n,H), t(n+4,H), t(n+8,H)) = +1</math> | |||
| ====HSV to RGB==== | |||
| ] | |||
| Given an HSV color with hue {{math|''H'' ∈ }}, and value {{math|''V'' ∈ }}, we can use the same strategy. First, we find chroma: | |||
| : <math>C = V \times S_V</math> | |||
| Then we can, again, find a point {{math|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value ''X'' for the second largest component of this color): | |||
| : <math>H^\prime = \frac{H}{60^\circ}</math> | |||
| : <math>X = C \times (1 - |H^\prime \bmod 2 - 1|)</math> | |||
| : <math> (R_1, G_1, B_1) = \begin{cases} | |||
| (C, X, 0) &\text{if } 0 \leq H^\prime < 1 \\ | |||
| (X, C, 0) &\text{if } 1 \leq H^\prime < 2 \\ | |||
| (0, C, X) &\text{if } 2 \leq H^\prime < 3 \\ | |||
| (0, X, C) &\text{if } 3 \leq H^\prime < 4 \\ | |||
| (X, 0, C) &\text{if } 4 \leq H^\prime < 5 \\ | |||
| (C, 0, X) &\text{if } 5 \leq H^\prime < 6 | |||
| \end{cases}</math> | |||
| As before, when <math>H^\prime</math> is an integer, "neighbouring" formulas would yield the same result. | |||
| Finally, we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match value: | Finally, we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match value: | ||
| : <math>m = V - C</math> | |||
| : <math>(R, G, B) = (R_1 + m, G_1 + m, B_1 + m)</math> | |||
| ===== HSV to RGB alternative ===== | |||
| :<math>\begin{align} | |||
| &m = V - C \\ | |||
| &(R, G, B) = (R_1 + m, G_1 + m, B_1 + m) | |||
| \end{align}</math> | |||
| Given a color with hue <math>H \in </math>, saturation <math>S=S_V \in </math>, and value <math>V \in </math>, first we define function : | |||
| === From HSL === | |||
| : <math>f(n) = V - VS \max(0, \min(k, 4-k, 1))</math> | |||
| Given an HSL color with hue {{nobr|''H'' ∈ }}, and lightness {{nobr|''L'' ∈ }}, we can use the same strategy. First, we find chroma: | |||
| where <math>k,n \in \mathbb R_{\geq 0}</math> and: | |||
| : <math>k = (n+\frac{H}{60^\circ}) \bmod 6</math> | |||
| And output R,G,B values (from <math>^3</math>) are: | |||
| :<math> | |||
| : <math>(R,G,B) = (f(5), f(3), f(1))</math> | |||
| C = | |||
| \begin{cases} | |||
| 2L \times S_{HSL}, &\mbox{if } L \leq \frac{1}{2} \\ | |||
| (2 - 2L) \times S_{HSL} &\mbox{if } L > \frac{1}{2} | |||
| \end{cases} | |||
| </math> | |||
| Above alternative equivalent formulas allow shorter implementation. In above formulas the <math>a\bmod b</math> returns also fractional part of module e.g. the formula <math> 7.4 \bmod 6 = 1.4</math>. The values of <math>k \in \mathbb R \land k \in [0,6)</math>. The base shape | |||
| Then we can, again, find a point {{nobr|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value ''X'' for the second largest component of this color): | |||
| : <math>t(n,H) = T(k) = \max(0, \min(k, 4-k, 1))</math> | |||
| is constructed as follows: <math>t_1 = \min(k,4-k)</math> is "triangle" for which non-negative values starts from k=0, highest point at k=2 and "ends" at k=4, then we change values bigger than one to one by <math>t_2 = \min(t_1,1) = \min(k,4-k,1)</math>, then change negative values to zero by <math>t = \max(t2,0)</math> – and we get (for <math>n=0</math>) something similar to green shape from Fig. 24 (which max value is 1 and min value is 0). The R,G,B functions of <math>H</math> use this shape transformed in following way: modulo-shifted on <math>X</math> (by <math>n</math>) (differently for R,G,B) scaled on <math>Y</math> (by <math>-VS</math>) and shifted on <math>Y</math> (by <math>V</math>). We observe following shape properties(Fig. 24 can help to get intuition about this): | |||
| : <math>t(n,H) = 1-t(n+3,H)</math> | |||
| : <math>\min(t(n,H), t(n+2,H), t(n+4,H)) = 0</math> | |||
| : <math>\max(t(n,H), t(n+2,H), t(n+4,H)) = 1</math> | |||
| ====HSI to RGB==== | |||
| :<math>\begin{align} | |||
| Given an HSI color with hue {{math|''H'' ∈ }}, and intensity {{math|''I'' ∈ }}, we can use the same strategy, in a slightly different order: | |||
| H^\prime &= \frac{H}{60^\circ} \\ | |||
| |
: <math>H^\prime = \frac{H}{60^\circ}</math> | ||
| : <math>Z = 1 - |H^\prime \;\bmod 2 - 1|</math> | |||
| \end{align}</math> | |||
| : <math>C = \frac{3 \cdot I \cdot S_I}{1 + Z}</math> | |||
| :<math> | |||
| : <math>X = C \cdot Z</math> | |||
| (R_1, G_1, B_1) = | |||
| \begin{cases} | |||
| Where <math>C</math> is the chroma. | |||
| (0, 0, 0) &\mbox{if } H \mbox{ is undefined} \\ | |||
| (C, X, 0) &\mbox{if } 0 \leq H^\prime < 1 \\ | |||
| Then we can, again, find a point {{math|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value ''X'' for the second largest component of this color): | |||
| (X, C, 0) &\mbox{if } 1 \leq H^\prime < 2 \\ | |||
| : <math>(R_1, G_1, B_1) = \begin{cases} | |||
| (0, C, X) &\mbox{if } 2 \leq H^\prime < 3 \\ | |||
| (0, 0, 0) &\text{if } H \text{ is undefined} \\ | |||
| |
(C, X, 0) &\text{if } 0 \leq H^\prime \leq 1 \\ | ||
| (X, C, 0) &\text{if } 1 \leq H^\prime \leq 2 \\ | |||
| (0, C, X) &\text{if } 2 \leq H^\prime \leq 3 \\ | |||
| \end{cases} | |||
| (0, X, C) &\text{if } 3 \leq H^\prime \leq 4 \\ | |||
| </math> | |||
| (X, 0, C) &\text{if } 4 \leq H^\prime \leq 5 \\ | |||
| (C, 0, X) &\text{if } 5 \leq H^\prime < 6 | |||
| \end{cases}</math> | |||
| Overlap (when <math>H^\prime</math> is an integer) occurs because two ways to calculate the value are equivalent: <math>X = 0</math> or <math>X = C</math>, as appropriate. | |||
| Finally, we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match lightness: | Finally, we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match lightness: | ||
| : <math>m = I \cdot (1 - S_I)</math> | |||
| : <math>(R, G, B) = (R_1 + m, G_1 + m, B_1 + m)</math> | |||
| ====Luma, chroma and hue to RGB==== | |||
| :<math>\begin{align} | |||
| Given a color with hue {{math|''H'' ∈ }}, and luma {{math|''{{prime|Y}}''<sub>601</sub> ∈ }},{{refn|group=upper-alpha |Some points in this cylinder fall out of ].}} we can again use the same strategy. Since we already have ''H'' and ''C'', we can straightaway find our point {{math|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube: | |||
| &m = L - \textstyle{\frac{1}{2}}C \\ | |||
| : <math>\begin{align} | |||
| &(R, G, B) = (R_1 + m, G_1 + m, B_1 + m) | |||
| H^\prime &= \frac{H}{60^\circ} \\ | |||
| X &= C \times (1 - |H^\prime \bmod 2 - 1|) | |||
| \end{align}</math> | \end{align}</math> | ||
| : <math>(R_1, G_1, B_1) = \begin{cases} | |||
| (0, 0, 0) &\text{if } H \text{ is undefined} \\ | |||
| (C, X, 0) &\text{if } 0 \leq H^\prime \leq 1 \\ | |||
| (X, C, 0) &\text{if } 1 \leq H^\prime \leq 2 \\ | |||
| (0, C, X) &\text{if } 2 \leq H^\prime \leq 3 \\ | |||
| (0, X, C) &\text{if } 3 \leq H^\prime \leq 4 \\ | |||
| (X, 0, C) &\text{if } 4 \leq H^\prime \leq 5 \\ | |||
| (C, 0, X) &\text{if } 5 \leq H^\prime < 6 | |||
| \end{cases}</math> | |||
| Overlap (when <math>H^\prime</math> is an integer) occurs because two ways to calculate the value are equivalent: <math>X = 0</math> or <math>X = C</math>, as appropriate. | |||
| === From luma/chroma/hue === | |||
| Given a color with hue {{nobr|''H'' ∈ }}, and luma {{nobr|''Y''′<sub>601</sub> ∈ }}, we can again use the same strategy. Since we already have ''H'' and ''C'', we can straightaway find our point {{nobr|(''R''<sub>1</sub>, ''G''<sub>1</sub>, ''B''<sub>1</sub>)}} along the bottom three faces of the RGB cube: | |||
| :<math>\begin{align} | |||
| H^\prime &= \frac{H}{60^\circ} \\ | |||
| X &= C (1 - |H^\prime \;\bmod 2 - 1|) | |||
| \end{align}</math> | |||
| :<math> | |||
| (R_1, G_1, B_1) = | |||
| \begin{cases} | |||
| (0, 0, 0) &\mbox{if } H \mbox{ is undefined} \\ | |||
| (C, X, 0) &\mbox{if } 0 \leq H^\prime < 1 \\ | |||
| (X, C, 0) &\mbox{if } 1 \leq H^\prime < 2 \\ | |||
| (0, C, X) &\mbox{if } 2 \leq H^\prime < 3 \\ | |||
| (0, X, C) &\mbox{if } 3 \leq H^\prime < 4 \\ | |||
| (X, 0, C) &\mbox{if } 4 \leq H^\prime < 5 \\ | |||
| (C, 0, X) &\mbox{if } 5 \leq H^\prime < 6 | |||
| \end{cases} | |||
| </math> | |||
| Then we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match luma: | Then we can find ''R'', ''G'', and ''B'' by adding the same amount to each component, to match luma: | ||
| : <math>m = Y^\prime_{601} - (0.30R_1 + 0.59G_1 + 0.11B_1)</math> | |||
| : <math>(R, G, B) = (R_1 + m, G_1 + m, B_1 + m)</math> | |||
| === Interconversion === | |||
| :<math>\begin{align} | |||
| &m = Y^\prime_{601} - (.30R_1 + .59G_1 + .11B_1) \\ | |||
| &(R, G, B) = (R_1 + m, G_1 + m, B_1 + m) | |||
| \end{align}</math> | |||
| == |
==== HSV to HSL ==== | ||
| {{div col}} | |||
| * Max K. Agoston (2005). . London: Springer. ISBN 1-85233-818-0. {{nobr|pp. 300–306}}. Agoston’s book contains a description of HSV and HSL, and algorithms in ] for converting to each from RGB, and back again. | |||
| * Heng-Da Cheng, Xihua Jiang, Angela Sun, and Jingli Wang (December 2001). . ''Pattern Recognition'' '''34'''(12): 2259–2281. This computer vision literature review briefly summarizes research in color image segmentation, including that using HSV and HSI representations. | |||
| * Mark D. Fairchild (2005). , 2nd edition. Addison-Wesley. This book doesn’t discuss HSL or HSV specifically, but is one of the most readable and precise resources about current color science. | |||
| * ], et al. (1995). , 2nd ed. Redwood City, CA: Addison-Wesley. ISBN 0-201-84840-6. The standard computer graphics textbook of the 1990s, this tome has a chapter full of algorithms for converting between color models, in ]. | |||
| * George H. Joblove and Donald Greenberg (August 1978). . ] '''12'''(3): 20–25. Joblove and Greenberg’s paper was the first describing the HSL model, which it compares to HSV. | |||
| * Rolf G. Kuehni (2003). . New York: Wiley. This book only briefly mentions HSL and HSV, but is a comprehensive description of color order systems through history. | |||
| * Haim Levkowitz and Gabor T. Herman (July 1993). “GLHS: A generalised lightness, hue and saturation color model”. ''CVGIP: Graphical Models and Image Processing'' '''55'''(4): 271–285. This paper explains how both HSL and HSV, as well as other similar models, can be thought of as specific variants of a more general “GLHS” model. Levkowitz and Herman provide pseudocode for converting from RGB to GLHS and back. | |||
| * Bruce MacEvoy (January 2010). . ''handprint.com''. Accessed January 2010. Especially the sections about and . MacEvoy’s extensive site about color science and paint mixing is one of the best resources on the web. On this page, he explains the color-making attributes, and the general goals and history of color order systems – including HSL and HSV – and their practical relevance to painters. | |||
| * Charles Poynton (1997). . This self-published frequently asked questions page, by digital video expert Charles Poynton, explains, among other things, why in his opinion these models “are useless for the specification of accurate color”, and should be abandoned in favor of more psychometrically relevant models. | |||
| * ] (August 1978). . ''Computer Graphics'' '''12'''(3): 12–19. This is the original paper describing the “hexcone” model, HSV. Smith was a researcher at ]’s Computer Graphics Lab. He describes HSV’s use in an early ] program. | |||
| * Anne Morgan Spalter (1999). ''The Computer in the Visual Arts''. Reading, MA: Addison-Wesley. This hefty book has a nice section describing HSL and HSV. | |||
| {{div col end}} | |||
| Given a color with hue <math>H_V \in </math>, and value <math>V \in </math>, | |||
| == Swatches == | |||
| Mouse over the swatches below to see the ''R'', ''G'', and ''B'' values for each swatch in a ]. | |||
| : <math>H_L = H_V</math> | |||
| : <math>S_L = \begin{cases} | |||
| 0 & \text{if } L=0 \text{ or } L=1 \\ | |||
| \frac{V-L}{\min(L,1-L)} & \text{otherwise} \\ | |||
| \end{cases}</math> | |||
| : <math>L = V\left(1 - \frac{S_V}{2}\right)</math> | |||
| ==== HSL to HSV ==== | |||
| Given a color with hue <math>H_L \in </math>, and luminance <math>L \in </math>, | |||
| : <math>H_V = H_L</math> | |||
| : <math>S_V = \begin{cases} | |||
| 0 & \text{if } V=0 \\ | |||
| 2\left(1-\frac{L}{V}\right) & \text{otherwise} \\ | |||
| \end{cases}</math> | |||
| : <math>V = L+S_L\min(L,1-L)</math> | |||
| === From RGB === | |||
| {{see also|#General approach}} | |||
| This is a reiteration of the previous conversion. | |||
| Value must be in range <math>R, G, B \in </math>. | |||
| With maximum component (i. e. value) | |||
| : <math>X_\text{max} := \max(R, G, B) =: V</math> | |||
| and minimum component | |||
| : <math>X_\text{min} := \min(R, G, B) = V-C</math>, | |||
| range (i. e. chroma) | |||
| : <math>C := X_\text{max} - X_\text{min} = 2(V-L) </math> | |||
| and mid-range (i. e. lightness) | |||
| : <math>L := \operatorname{mid}(R, G, B) = \frac{X_\text{max} + X_\text{min}}{2} = V-\frac{C}{2}</math>, | |||
| we get common hue: | |||
| : <math>H := \begin{cases} | |||
| 0, & \text{if } C = 0 \\ | |||
| 60^\circ \cdot \left( \frac {G - B} {C} \mod 6 \right), & \text{if } V = R \\ | |||
| 60^\circ \cdot \left( \frac {B - R} {C} + 2 \right), & \text{if } V = G \\ | |||
| 60^\circ \cdot \left( \frac {R - G} {C} + 4 \right), & \text{if } V = B | |||
| \end{cases}</math> | |||
| and distinct saturations: | |||
| : <math>S_V := \begin{cases} | |||
| 0, &\text{if } V=0\\ | |||
| \frac{C}{V}, &{\text{otherwise}} | |||
| \end{cases}</math> | |||
| : <math>S_L := \begin{cases} | |||
| 0, &\text{if }L=0\text{ or }L=1\\ | |||
| \frac {C}{1-\left\vert 2V-C-1\right\vert} | |||
| =\frac{2(V-L)}{ 1-\left\vert 2L-1\right\vert} | |||
| =\frac{V-L}{\min(L,1-L)}, | |||
| & \text{otherwise} | |||
| \end{cases}</math> | |||
| ==Swatches== | |||
| Mouse over the ] below to see the ''R'', ''G'', and ''B'' values for each swatch in a ]. | |||
| ===HSL=== | |||
| {{hsl-swatches}} | |||
| === HSV === | === HSV === | ||
| {{hsv-swatches}} | {{hsv-swatches}} | ||
| == |
==See also== | ||
| * ] | |||
| {{hsl-swatches}} | |||
| * ] | |||
| == |
==Notes== | ||
| {{reflist| |
{{reflist|group=upper-alpha |35em}} | ||
| ==References== | |||
| {{reflist}} | |||
| ==Bibliography== | |||
| * {{cite book|ref=Agoston |author=Agoston, Max K. |year=2005|url=https://books.google.com/books?id=fGX8yC-4vXUC&pg=PA300 |title=Computer Graphics and Geometric Modeling: Implementation and Algorithms|place= London|publisher= Springer|isbn=978-1-85233-818-3|pages=300–306}} Agoston's book contains a description of HSV and HSL, and algorithms in ] for converting to each from RGB, and back again. | |||
| * {{cite journal|ref=Cheng |author1=Cheng, Heng-Da |author2=Jiang, Xihua |author3=Sun, Angela |author4=Wang, Jingli |doi=10.1016/S0031-3203(00)00149-7 |title=Color image segmentation: Advances and prospects |year=2001 |journal=Pattern Recognition |volume=34 |issue=12 |page=2259|bibcode=2001PatRe..34.2259C |citeseerx=10.1.1.119.2886 |s2cid=205904573 }} This computer vision literature review briefly summarizes research in color image segmentation, including that using HSV and HSI representations. | |||
| * {{cite book|ref= Fairchild|author=Fairchild, Mark D. |year=2005|url=http://www.cis.rit.edu/fairchild/CAM.html |title=Color Appearance Models|edition= 2nd|publisher= Addison-Wesley}} This book doesn't discuss HSL or HSV specifically, but is one of the most readable and precise resources about current color science. | |||
| * {{cite book|ref= Foley|author-link=James D. Foley|author=Foley, J. D.|year=1995|url=http://www.pearsonhighered.com/educator/academic/product/0,,0201848406,00%2Ben-USS_01DBC.html |title=Computer Graphics: Principles and Practice|edition= 2nd |place=Redwood City, CA|publisher= Addison-Wesley|isbn=978-0-201-84840-3|display-authors=etal}} The standard computer graphics textbook of the 1990s, this tome has a chapter full of algorithms for converting between color models, in ]. | |||
| * {{cite book|ref=Hanbury2002|author1=Hanbury, Allan |author2=Serra, Jean |date=December 2002|title=A 3D-polar Coordinate Colour Representation Suitable for Image Analysis|work= Pattern Recognition and Image Processing Group Technical Report 77|place= Vienna, Austria|publisher= Vienna University of Technology}} | |||
| * {{cite journal|ref=Hanbury2008|first1=Allan |last1=Hanbury |year=2008 |url=http://muscle.ercim.eu/images/DocumentPDF/Hanbury_PRL.pdf |doi=10.1016/j.patrec.2007.11.002|title=Constructing cylindrical coordinate colour spaces|journal=Pattern Recognition Letters|volume=29|issue=4|pages=494–500|bibcode=2008PaReL..29..494H |citeseerx=10.1.1.211.6425 }} | |||
| * {{cite journal|ref=Joblove|author1=Joblove, George H. |author2=Greenberg, Donald |date=August 1978 |title=Color spaces for computer graphics |journal=] |volume=12 |issue=3 |pages=20–25 |doi=10.1145/965139.807362 |url=https://papers.cumincad.org/data/works/att/634c.content.pdf }} Joblove and Greenberg's paper was the first describing the HSL model, which it compares to HSV. | |||
| * {{cite book|ref=Kuehni|author= Kuehni, Rolf G. |year=2003|title=Color Space and Its Divisions: Color Order from Antiquity to the present|place=New York|publisher= Wiley|isbn=978-0-471-32670-0}} This book only briefly mentions HSL and HSV, but is a comprehensive description of color order systems through history. | |||
| * {{cite journal|ref=Levkowitz|author1=Levkowitz, Haim |author2=Herman, Gabor T. |year=1993 |title=GLHS: A Generalized Lightness, Hue and Saturation Color Model|journal=] |volume=55 |issue=4 |pages=271–285 |doi=10.1006/cgip.1993.1019}} This paper explains how both HSL and HSV, as well as other similar models, can be thought of as specific variants of a more general "GLHS" model. Levkowitz and Herman provide pseudocode for converting from RGB to GLHS and back. | |||
| * {{cite web|ref=MacEvoy|author=MacEvoy, Bruce |date=January 2010|url=http://www.handprint.com/LS/CVS/color.html |title=Color Vision|work=handprint.com}}. Especially the sections about and . MacEvoy's extensive site about color science and paint mixing is one of the best resources on the web. On this page, he explains the color-making attributes, and the general goals and history of color order systems – including HSL and HSV – and their practical relevance to painters. | |||
| * {{cite web|ref=Poynton |author=Poynton, Charles |year=1997|url=http://www.poynton.com/ColorFAQ.html |title=Frequently Asked Questions About Color |website=poynton.com}} This self-published frequently asked questions page, by digital video expert Charles Poynton, explains, among other things, why in his opinion these models "are useless for the specification of accurate color", and should be abandoned in favor of more psychometrically relevant models. | |||
| * {{cite web|ref=Poynton2008 |author=Poynton, Charles |year=2008|url=http://poynton.com/papers/YUV_and_luminance_harmful.html |title=''YUV'' and ''luminance'' considered harmful |website=poynton.com |access-date=August 30, 2017}} | |||
| * {{cite journal|ref=Smith|author=Smith, Alvy Ray |author-link=Alvy Ray Smith|date=August 1978|title=Color gamut transform pairs|journal=Computer Graphics|volume=12|issue=3|pages=12–19|doi=10.1145/965139.807361|doi-access=free}} This is the original paper describing the "hexcone" model, HSV. Smith was a researcher at ]'s Computer Graphics Lab. He describes HSV's use in an early ] program. | |||
| ==External links== | ==External links== | ||
| * | * | ||
| * by Hector Zenil, ]. | * by Hector Zenil, ]. | ||
| * by CodeBeautify. | |||
| {{color space|state=expanded}} | {{color space|state=expanded}} | ||
| {{DEFAULTSORT:Hsl And Hsv}} | |||
| ] | ] | ||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 20:03, 21 January 2025
Alternative representations of the RGB color model
HSL and HSV are the two most common cylindrical-coordinate representations of points in an RGB color model. The two representations rearrange the geometry of RGB in an attempt to be more intuitive and perceptually relevant than the cartesian (cube) representation. Developed in the 1970s for computer graphics applications, HSL and HSV are used today in color pickers, in image editing software, and less commonly in image analysis and computer vision.
HSL stands for hue, saturation, and lightness, and is often also called HLS. HSV stands for hue, saturation, and value, and is also often called HSB (B for brightness). A third model, common in computer vision applications, is HSI, for hue, saturation, and intensity. However, while typically consistent, these definitions are not standardized, and any of these abbreviations might be used for any of these three or several other related cylindrical models. (For technical definitions of these terms, see below.)
In each cylinder, the angle around the central vertical axis corresponds to "hue", the distance from the axis corresponds to "saturation", and the distance along the axis corresponds to "lightness", "value" or "brightness". Note that while "hue" in HSL and HSV refers to the same attribute, their definitions of "saturation" differ dramatically. Because HSL and HSV are simple transformations of device-dependent RGB models, the physical colors they define depend on the colors of the red, green, and blue primaries of the device or of the particular RGB space, and on the gamma correction used to represent the amounts of those primaries. Each unique RGB device therefore has unique HSL and HSV spaces to accompany it, and numerical HSL or HSV values describe a different color for each basis RGB space.
Both of these representations are used widely in computer graphics, and one or the other of them is often more convenient than RGB, but both are also criticized for not adequately separating color-making attributes, or for their lack of perceptual uniformity. Other more computationally intensive models, such as CIELAB or CIECAM02 are said to better achieve these goals.
Basic principle
 Fig. 2a. HSL cylinder.
Fig. 2a. HSL cylinder. Fig. 2b. HSV cylinder.
Fig. 2b. HSV cylinder.
HSL and HSV are both cylindrical geometries (fig. 2), with hue, their angular dimension, starting at the red primary at 0°, passing through the green primary at 120° and the blue primary at 240°, and then wrapping back to red at 360°. In each geometry, the central vertical axis comprises the neutral, achromatic, or gray colors ranging, from top to bottom, white at lightness 1 (value 1) to black at lightness 0 (value 0).
In both geometries, the additive primary and secondary colors – red, yellow, green, cyan, blue and magenta – and linear mixtures between adjacent pairs of them, sometimes called pure colors, are arranged around the outside edge of the cylinder with saturation 1. These saturated colors have lightness 0.5 in HSL, while in HSV they have value 1. Mixing these pure colors with black – producing so-called shades – leaves saturation unchanged. In HSL, saturation is also unchanged by tinting with white, and only mixtures with both black and white – called tones – have saturation less than 1. In HSV, tinting alone reduces saturation.

 Fig. 3a–b. If we plot hue and (a) HSL lightness or (b) HSV value against chroma (range of RGB values) rather than saturation (chroma over maximum chroma for that slice), the resulting solid is a bicone or cone, respectively, not a cylinder. Such diagrams often claim to represent HSL or HSV directly, with the chroma dimension confusingly labeled "saturation".
Fig. 3a–b. If we plot hue and (a) HSL lightness or (b) HSV value against chroma (range of RGB values) rather than saturation (chroma over maximum chroma for that slice), the resulting solid is a bicone or cone, respectively, not a cylinder. Such diagrams often claim to represent HSL or HSV directly, with the chroma dimension confusingly labeled "saturation".
Because these definitions of saturation – in which very dark (in both models) or very light (in HSL) near-neutral colors are considered fully saturated (for instance, from the bottom right in the sliced HSL cylinder or from the top right) – conflict with the intuitive notion of color purity, often a conic or biconic solid is drawn instead (fig. 3), with what this article calls chroma as its radial dimension (equal to the range of the RGB values), instead of saturation (where the saturation is equal to the chroma over the maximum chroma in that slice of the (bi)cone). Confusingly, such diagrams usually label this radial dimension "saturation", blurring or erasing the distinction between saturation and chroma. As described below, computing chroma is a helpful step in the derivation of each model. Because such an intermediate model – with dimensions hue, chroma, and HSV value or HSL lightness – takes the shape of a cone or bicone, HSV is often called the "hexcone model" while HSL is often called the "bi-hexcone model" (fig. 8).
Motivation
See also: Color theory, RGB color model, and RGB color space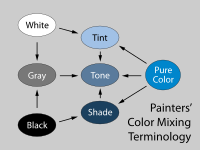 Fig. 4. Painters long mixed colors by combining relatively bright pigments with black and white. Mixtures with white are called tints, mixtures with black are called shades, and mixtures with both are called tones. See Tints and shades.
Fig. 4. Painters long mixed colors by combining relatively bright pigments with black and white. Mixtures with white are called tints, mixtures with black are called shades, and mixtures with both are called tones. See Tints and shades. Fig. 5. This 1916 color model by German chemist Wilhelm Ostwald exemplifies the "mixtures with white and black" approach, organizing 24 "pure" colors into a hue circle, and colors of each hue into a triangle. The model thus takes the shape of a bicone.
Fig. 5. This 1916 color model by German chemist Wilhelm Ostwald exemplifies the "mixtures with white and black" approach, organizing 24 "pure" colors into a hue circle, and colors of each hue into a triangle. The model thus takes the shape of a bicone.
 Fig. 6a. The RGB gamut can be arranged in a cube.
Fig. 6a. The RGB gamut can be arranged in a cube. Fig. 6b. The same image, with a portion removed for clarity.
Fig. 6b. The same image, with a portion removed for clarity.
 Fig. 7. Tektronix graphics terminals used the earliest commercial implementation of HSL, in 1979. This diagram, from a patent filed in 1983, shows the bicone geometry underlying the model.
Fig. 7. Tektronix graphics terminals used the earliest commercial implementation of HSL, in 1979. This diagram, from a patent filed in 1983, shows the bicone geometry underlying the model.
Most televisions, computer displays, and projectors produce colors by combining red, green, and blue light in varying intensities – the so-called RGB additive primary colors. The resulting mixtures in RGB color space can reproduce a wide variety of colors (called a gamut); however, the relationship between the constituent amounts of red, green, and blue light and the resulting color is unintuitive, especially for inexperienced users, and for users familiar with subtractive color mixing of paints or traditional artists' models based on tints and shades (fig. 4). Furthermore, neither additive nor subtractive color models define color relationships the same way the human eye does.
For example, imagine we have an RGB display whose color is controlled by three sliders ranging from 0–255, one controlling the intensity of each of the red, green, and blue primaries. If we begin with a relatively colorful orange , with sRGB values R = 217, G = 118, B = 33, and want to reduce its colorfulness by half to a less saturated orange , we would need to drag the sliders to decrease R by 31, increase G by 24, and increase B by 59, as pictured below.
Beginning in the 1950s, color television broadcasts used a compatible color system whereby "luminance" and "chrominance" signals were encoded separately, so that existing unmodified black-and-white televisions could still receive color broadcasts and show a monochrome image.
In an attempt to accommodate more traditional and intuitive color mixing models, computer graphics pioneers at PARC and NYIT introduced the HSV model for computer display technology in the mid-1970s, formally described by Alvy Ray Smith in the August 1978 issue of Computer Graphics. In the same issue, Joblove and Greenberg described the HSL model – whose dimensions they labeled hue, relative chroma, and intensity – and compared it to HSV (fig. 1). Their model was based more upon how colors are organized and conceptualized in human vision in terms of other color-making attributes, such as hue, lightness, and chroma; as well as upon traditional color mixing methods – e.g., in painting – that involve mixing brightly colored pigments with black or white to achieve lighter, darker, or less colorful colors.
The following year, 1979, at SIGGRAPH, Tektronix introduced graphics terminals using HSL for color designation, and the Computer Graphics Standards Committee recommended it in their annual status report (fig. 7). These models were useful not only because they were more intuitive than raw RGB values, but also because the conversions to and from RGB were extremely fast to compute: they could run in real time on the hardware of the 1970s. Consequently, these models and similar ones have become ubiquitous throughout image editing and graphics software since then. Some of their uses are described below.
Formal derivation

Color-making attributes
See also: Color visionThe dimensions of the HSL and HSV geometries – simple transformations of the not-perceptually-based RGB model – are not directly related to the photometric color-making attributes of the same names, as defined by scientists such as the CIE or ASTM. Nonetheless, it is worth reviewing those definitions before leaping into the derivation of our models. For the definitions of color-making attributes which follow, see:
- Hue
- The "attribute of a visual sensation according to which an area appears to be similar to one of the perceived colors: red, yellow, green, and blue, or to a combination of two of them".
- Radiance (Le,Ω)
- The radiant power of light passing through a particular surface per unit solid angle per unit projected area, measured in SI units in watt per steradian per square metre (W·sr·m).
- Luminance (Y or Lv,Ω)
- The radiance weighted by the effect of each wavelength on a typical human observer, measured in SI units in candela per square meter (cd/m). Often the term luminance is used for the relative luminance, Y/Yn, where Yn is the luminance of the reference white point.
- Luma (Y′)
- The weighted sum of gamma-corrected R′, G′, and B′ values, and used in Y′CbCr, for JPEG compression and video transmission.
- Brightness (or value)
- The "attribute of a visual sensation according to which an area appears to emit more or less light".
- Lightness
- The "brightness relative to the brightness of a similarly illuminated white".
- Colorfulness
- The "attribute of a visual sensation according to which the perceived color of an area appears to be more or less chromatic".
- Chroma
- The "colorfulness relative to the brightness of a similarly illuminated white".
- Saturation
- The "colorfulness of a stimulus relative to its own brightness".
Brightness and colorfulness are absolute measures, which usually describe the spectral distribution of light entering the eye, while lightness and chroma are measured relative to some white point, and are thus often used for descriptions of surface colors, remaining roughly constant even as brightness and colorfulness change with different illumination. Saturation can be defined as either the ratio of colorfulness to brightness, or that of chroma to lightness.
General approach
HSL, HSV, and related models can be derived via geometric strategies, or can be thought of as specific instances of a "generalized LHS model". The HSL and HSV model-builders took an RGB cube – with constituent amounts of red, green, and blue light in a color denoted R, G, B ∈ – and tilted it on its corner, so that black rested at the origin with white directly above it along the vertical axis, then measured the hue of the colors in the cube by their angle around that axis, starting with red at 0°. Then they came up with a characterization of brightness/value/lightness, and defined saturation to range from 0 along the axis to 1 at the most colorful point for each pair of other parameters.
Hue and chroma
See also: Hue and Chrominance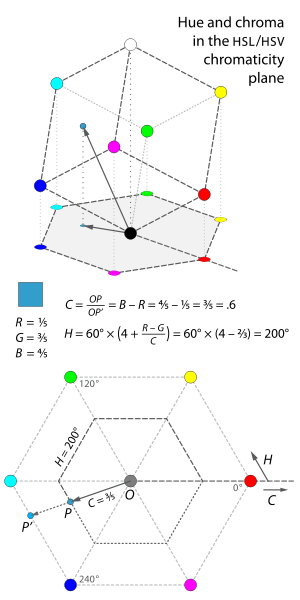
In each of our models, we calculate both hue and what this article will call chroma, after Joblove and Greenberg (1978), in the same way – that is, the hue of a color has the same numerical values in all of these models, as does its chroma. If we take our tilted RGB cube, and project it onto the "chromaticity plane" perpendicular to the neutral axis, our projection takes the shape of a hexagon, with red, yellow, green, cyan, blue, and magenta at its corners (fig. 9). Hue is roughly the angle of the vector to a point in the projection, with red at 0°, while chroma is roughly the distance of the point from the origin.
More precisely, both hue and chroma in this model are defined with respect to the hexagonal shape of the projection. The chroma is the proportion of the distance from the origin to the edge of the hexagon. In the lower part of the adjacent diagram, this is the ratio of lengths OP/OP′, or alternatively the ratio of the radii of the two hexagons. This ratio is the difference between the largest and smallest values among R, G, or B in a color. To make our definitions easier to write, we'll define these maximum, minimum, and chroma component values as M, m, and C, respectively.
To understand why chroma can be written as M − m, notice that any neutral color, with R = G = B, projects onto the origin and so has 0 chroma. Thus if we add or subtract the same amount from all three of R, G, and B, we move vertically within our tilted cube, and do not change the projection. Therefore, any two colors of (R, G, B) and (R − m, G − m, B − m) project on the same point, and have the same chroma. The chroma of a color with one of its components equal to zero (m = 0) is simply the maximum of the other two components. This chroma is M in the particular case of a color with a zero component, and M − m in general.
The hue is the proportion of the distance around the edge of the hexagon which passes through the projected point, originally measured on the range but now typically measured in degrees [0°, 360°). For points which project onto the origin in the chromaticity plane (i.e., grays), hue is undefined. Mathematically, this definition of hue is written piecewise:
Sometimes, neutral colors (i.e. with C = 0) are assigned a hue of 0° for convenience of representation.
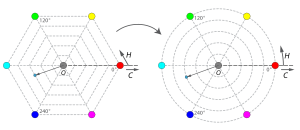
These definitions amount to a geometric warping of hexagons into circles: each side of the hexagon is mapped linearly onto a 60° arc of the circle (fig. 10). After such a transformation, hue is precisely the angle around the origin and chroma the distance from the origin: the angle and magnitude of the vector pointing to a color.
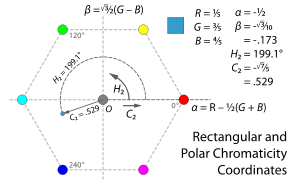
Sometimes for image analysis applications, this hexagon-to-circle transformation is skipped, and hue and chroma (we'll denote these H2 and C2) are defined by the usual cartesian-to-polar coordinate transformations (fig. 11). The easiest way to derive those is via a pair of cartesian chromaticity coordinates which we'll call α and β:
(The atan2 function, a "two-argument arctangent", computes the angle from a cartesian coordinate pair.)
Notice that these two definitions of hue (H and H2) nearly coincide, with a maximum difference between them for any color of about 1.12° – which occurs at twelve particular hues, for instance H = 13.38°, H2 = 12.26° – and with H = H2 for every multiple of 30°. The two definitions of chroma (C and C2) differ more substantially: they are equal at the corners of our hexagon, but at points halfway between two corners, such as H = H2 = 30°, we have C = 1, but a difference of about 13.4%.
Lightness
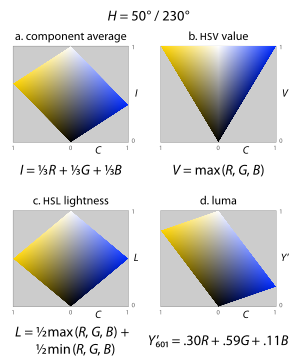
While the definition of hue is relatively uncontroversial – it roughly satisfies the criterion that colors of the same perceived hue should have the same numerical hue – the definition of a lightness or value dimension is less obvious: there are several possibilities depending on the purpose and goals of the representation. Here are four of the most common (fig. 12; three of these are also shown in fig. 8):
- The simplest definition is just the arithmetic mean, i.e. average, of the three components, in the HSI model called intensity (fig. 12a). This is simply the projection of a point onto the neutral axis – the vertical height of a point in our tilted cube. The advantage is that, together with Euclidean-distance calculations of hue and chroma, this representation preserves distances and angles from the geometry of the RGB cube.
- In the HSV "hexcone" model, value is defined as the largest component of a color, our M above (fig. 12b). This places all three primaries, and also all of the "secondary colors" – cyan, yellow, and magenta – into a plane with white, forming a hexagonal pyramid out of the RGB cube.
- In the HSL "bi-hexcone" model, lightness is defined as the average of the largest and smallest color components (fig. 12c), i.e. the mid-range of the RGB components. This definition also puts the primary and secondary colors into a plane, but a plane passing halfway between white and black. The resulting color solid is a double-cone similar to Ostwald's, shown above.
- A more perceptually relevant alternative is to use luma, Y′, as a lightness dimension (fig. 12d). Luma is the weighted average of gamma-corrected R, G, and B, based on their contribution to perceived lightness, long used as the monochromatic dimension in color television broadcast. For sRGB, the Rec. 709 primaries yield Y′709, digital NTSC uses Y′601 according to Rec. 601 and some other primaries are also in use which result in different coefficients.
- (SDTV)
- (Adobe)
- (HDTV)
- (UHDTV, HDR)
All four of these leave the neutral axis alone. That is, for colors with R = G = B, any of the four formulations yields a lightness equal to the value of R, G, or B.
For a graphical comparison, see fig. 13 below.
Saturation
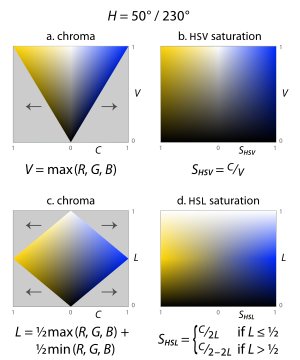
When encoding colors in a hue/lightness/chroma or hue/value/chroma model (using the definitions from the previous two sections), not all combinations of lightness (or value) and chroma are meaningful: that is, half of the colors denotable using H ∈ , and V ∈ fall outside the RGB gamut (the gray parts of the slices in figure 14). The creators of these models considered this a problem for some uses. For example, in a color selection interface with two of the dimensions in a rectangle and the third on a slider, half of that rectangle is made of unused space. Now imagine we have a slider for lightness: the user's intent when adjusting this slider is potentially ambiguous: how should the software deal with out-of-gamut colors? Or conversely, If the user has selected as colorful as possible a dark purple , and then shifts the lightness slider upward, what should be done: would the user prefer to see a lighter purple still as colorful as possible for the given hue and lightness , or a lighter purple of exactly the same chroma as the original color ?
To solve problems such as these, the HSL and HSV models scale the chroma so that it always fits into the range for every combination of hue and lightness or value, calling the new attribute saturation in both cases (fig. 14). To calculate either, simply divide the chroma by the maximum chroma for that value or lightness.

The HSI model commonly used for computer vision, which takes H2 as a hue dimension and the component average I ("intensity") as a lightness dimension, does not attempt to "fill" a cylinder by its definition of saturation. Instead of presenting color choice or modification interfaces to end users, the goal of HSI is to facilitate separation of shapes in an image. Saturation is therefore defined in line with the psychometric definition: chroma relative to lightness (fig. 15). See the Use in image analysis section of this article.
Using the same name for these three different definitions of saturation leads to some confusion, as the three attributes describe substantially different color relationships; in HSV and HSI, the term roughly matches the psychometric definition, of a chroma of a color relative to its own lightness, but in HSL it does not come close. Even worse, the word saturation is also often used for one of the measurements we call chroma above (C or C2).
Examples
All parameter values shown below are given as values in the interval , except those for H and H2, which are in the interval [0°, 360°).
| Color | R | G | B | H | H2 | C | C2 | V | L | I | Y′601 | SHSV | SHSL | SHSI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #FFFFFF | 1.000 | 1.000 | 1.000 | n/a | n/a | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.000 | 0.000 | 0.000 |
| #808080 | 0.500 | 0.500 | 0.500 | n/a | n/a | 0.000 | 0.000 | 0.500 | 0.500 | 0.500 | 0.500 | 0.000 | 0.000 | 0.000 |
| #000000 | 0.000 | 0.000 | 0.000 | n/a | n/a | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| #FF0000 | 1.000 | 0.000 | 0.000 | 0.0° | 0.0° | 1.000 | 1.000 | 1.000 | 0.500 | 0.333 | 0.299 | 1.000 | 1.000 | 1.000 |
| #BFBF00 | 0.750 | 0.750 | 0.000 | 60.0° | 60.0° | 0.750 | 0.750 | 0.750 | 0.375 | 0.500 | 0.664 | 1.000 | 1.000 | 1.000 |
| #008000 | 0.000 | 0.500 | 0.000 | 120.0° | 120.0° | 0.500 | 0.500 | 0.500 | 0.250 | 0.167 | 0.293 | 1.000 | 1.000 | 1.000 |
| #80FFFF | 0.500 | 1.000 | 1.000 | 180.0° | 180.0° | 0.500 | 0.500 | 1.000 | 0.750 | 0.833 | 0.850 | 0.500 | 1.000 | 0.400 |
| #8080FF | 0.500 | 0.500 | 1.000 | 240.0° | 240.0° | 0.500 | 0.500 | 1.000 | 0.750 | 0.667 | 0.557 | 0.500 | 1.000 | 0.250 |
| #BF40BF | 0.750 | 0.250 | 0.750 | 300.0° | 300.0° | 0.500 | 0.500 | 0.750 | 0.500 | 0.583 | 0.457 | 0.667 | 0.500 | 0.571 |
| #A0A424 | 0.628 | 0.643 | 0.142 | 61.8° | 61.5° | 0.501 | 0.494 | 0.643 | 0.393 | 0.471 | 0.581 | 0.779 | 0.638 | 0.699 |
| #411BEA | 0.255 | 0.104 | 0.918 | 251.1° | 250.0° | 0.814 | 0.750 | 0.918 | 0.511 | 0.426 | 0.242 | 0.887 | 0.832 | 0.756 |
| #1EAC41 | 0.116 | 0.675 | 0.255 | 134.9° | 133.8° | 0.559 | 0.504 | 0.675 | 0.396 | 0.349 | 0.460 | 0.828 | 0.707 | 0.667 |
| #F0C80E | 0.941 | 0.785 | 0.053 | 49.5° | 50.5° | 0.888 | 0.821 | 0.941 | 0.497 | 0.593 | 0.748 | 0.944 | 0.893 | 0.911 |
| #B430E5 | 0.704 | 0.187 | 0.897 | 283.7° | 284.8° | 0.710 | 0.636 | 0.897 | 0.542 | 0.596 | 0.423 | 0.792 | 0.775 | 0.686 |
| #ED7651 | 0.931 | 0.463 | 0.316 | 14.3° | 13.2° | 0.615 | 0.556 | 0.931 | 0.624 | 0.570 | 0.586 | 0.661 | 0.817 | 0.446 |
| #FEF888 | 0.998 | 0.974 | 0.532 | 56.9° | 57.4° | 0.466 | 0.454 | 0.998 | 0.765 | 0.835 | 0.931 | 0.467 | 0.991 | 0.363 |
| #19CB97 | 0.099 | 0.795 | 0.591 | 162.4° | 163.4° | 0.696 | 0.620 | 0.795 | 0.447 | 0.495 | 0.564 | 0.875 | 0.779 | 0.800 |
| #362698 | 0.211 | 0.149 | 0.597 | 248.3° | 247.3° | 0.448 | 0.420 | 0.597 | 0.373 | 0.319 | 0.219 | 0.750 | 0.601 | 0.533 |
| #7E7EB8 | 0.495 | 0.493 | 0.721 | 240.5° | 240.4° | 0.228 | 0.227 | 0.721 | 0.607 | 0.570 | 0.520 | 0.316 | 0.290 | 0.135 |
Use in end-user software
See also: Color picker and Image editing
- SGI IRIX 5, c. 1995;
- Adobe Photoshop, c. 1990;
- IBM OS/2 Warp 3, c. 1994;
- Apple Macintosh System 7, c. 1996;
- Fractal Design Painter, c. 1993;
- Microsoft Windows 3.1, c. 1992;
- NeXTSTEP, c. 1995.
The original purpose of HSL and HSV and similar models, and their most common current application, is in color selection tools. At their simplest, some such color pickers provide three sliders, one for each attribute. Most, however, show a two-dimensional slice through the model, along with a slider controlling which particular slice is shown. The latter type of GUI exhibits great variety, because of the choice of cylinders, hexagonal prisms, or cones/bicones that the models suggest (see the diagram near the top of the page). Several color choosers from the 1990s are shown to the right, most of which have remained nearly unchanged in the intervening time: today, nearly every computer color chooser uses HSL or HSV, at least as an option. Some more sophisticated variants are designed for choosing whole sets of colors, basing their suggestions of compatible colors on the HSL or HSV relationships between them.
Most web applications needing color selection also base their tools on HSL or HSV, and pre-packaged open source color choosers exist for most major web front-end frameworks. The CSS 3 specification allows web authors to specify colors for their pages directly with HSL coordinates.
HSL and HSV are sometimes used to define gradients for data visualization, as in maps or medical images. For example, the popular GIS program ArcGIS historically applied customizable HSV-based gradients to numerical geographical data.
 |
 |
Image editing software also commonly includes tools for adjusting colors with reference to HSL or HSV coordinates, or to coordinates in a model based on the "intensity" or luma defined above. In particular, tools with a pair of "hue" and "saturation" sliders are commonplace, dating to at least the late-1980s, but various more complicated color tools have also been implemented. For instance, the Unix image viewer and color editor xv allowed six user-definable hue (H) ranges to be rotated and resized, included a dial-like control for saturation (SHSV), and a curves-like interface for controlling value (V) – see fig. 17. The image editor Picture Window Pro includes a "color correction" tool which affords complex remapping of points in a hue/saturation plane relative to either HSL or HSV space.
Video editors also use these models. For example, both Avid and Final Cut Pro include color tools based on HSL or a similar geometry for use adjusting the color in video. With the Avid tool, users pick a vector by clicking a point within the hue/saturation circle to shift all the colors at some lightness level (shadows, mid-tones, highlights) by that vector.
Since version 4.0, Adobe Photoshop's "Luminosity", "Hue", "Saturation", and "Color" blend modes composite layers using a luma/chroma/hue color geometry. These have been copied widely, but several imitators use the HSL (e.g. PhotoImpact, Paint Shop Pro) or HSV geometries instead.
Use in image analysis
See also: Computer vision and Image analysisHSL, HSV, HSI, or related models are often used in computer vision and image analysis for feature detection or image segmentation. The applications of such tools include object detection, for instance in robot vision; object recognition, for instance of faces, text, or license plates; content-based image retrieval; and analysis of medical images.
For the most part, computer vision algorithms used on color images are straightforward extensions to algorithms designed for grayscale images, for instance k-means or fuzzy clustering of pixel colors, or canny edge detection. At the simplest, each color component is separately passed through the same algorithm. It is important, therefore, that the features of interest can be distinguished in the color dimensions used. Because the R, G, and B components of an object's color in a digital image are all correlated with the amount of light hitting the object, and therefore with each other, image descriptions in terms of those components make object discrimination difficult. Descriptions in terms of hue/lightness/chroma or hue/lightness/saturation are often more relevant.
Starting in the late 1970s, transformations like HSV or HSI were used as a compromise between effectiveness for segmentation and computational complexity. They can be thought of as similar in approach and intent to the neural processing used by human color vision, without agreeing in particulars: if the goal is object detection, roughly separating hue, lightness, and chroma or saturation is effective, but there is no particular reason to strictly mimic human color response. John Kender's 1976 master's thesis proposed the HSI model. Ohta et al. (1980) instead used a model made up of dimensions similar to those we have called I, α, and β. In recent years, such models have continued to see wide use, as their performance compares favorably with more complex models, and their computational simplicity remains compelling.
Disadvantages
 Fig 20a. The sRGB gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced by hue angle, and are of unequal length. The primaries also have different L* values.
Fig 20a. The sRGB gamut mapped in CIELAB space. Notice that the lines pointing to the red, green, and blue primaries are not evenly spaced by hue angle, and are of unequal length. The primaries also have different L* values. Fig 20b. The Adobe RGB gamut mapped in CIELAB space. Also notice that these two RGB spaces have different gamuts, and thus will have different HSL and HSV representations.
Fig 20b. The Adobe RGB gamut mapped in CIELAB space. Also notice that these two RGB spaces have different gamuts, and thus will have different HSL and HSV representations.
While HSL, HSV, and related spaces serve well enough to, for instance, choose a single color, they ignore much of the complexity of color appearance. Essentially, they trade off perceptual relevance for computation speed, from a time in computing history (high-end 1970s graphics workstations, or mid-1990s consumer desktops) when more sophisticated models would have been too computationally expensive.
HSL and HSV are simple transformations of RGB which preserve symmetries in the RGB cube unrelated to human perception, such that its R, G, and B corners are equidistant from the neutral axis, and equally spaced around it. If we plot the RGB gamut in a more perceptually-uniform space, such as CIELAB (see below), it becomes immediately clear that the red, green, and blue primaries do not have the same lightness or chroma, or evenly spaced hues. Furthermore, different RGB displays use different primaries, and so have different gamuts. Because HSL and HSV are defined purely with reference to some RGB space, they are not absolute color spaces: to specify a color precisely requires reporting not only HSL or HSV values, but also the characteristics of the RGB space they are based on, including the gamma correction in use.
If we take an image and extract the hue, saturation, and lightness or value components, and then compare these to the components of the same name as defined by color scientists, we can quickly see the difference, perceptually. For example, examine the following images of a fire breather (fig. 13). The original is in the sRGB colorspace. CIELAB L* is a CIE-defined achromatic lightness quantity (dependent solely on the perceptually achromatic luminance Y, but not the mixed-chromatic components X or Z, of the CIEXYZ colorspace from which the sRGB colorspace itself is derived), and it is plain that this appears similar in perceptual lightness to the original color image. Luma is roughly similar, but differs somewhat at high chroma, where it deviates most from depending solely on the true achromatic luminance (Y, or equivalently L*) and is influenced by the colorimetric chromaticity (x,y, or equivalently, a*,b* of CIELAB). HSL L and HSV V, by contrast, diverge substantially from perceptual lightness.
 Fig. 13a. Color photograph (sRGB colorspace).
Fig. 13a. Color photograph (sRGB colorspace). Fig. 13b. CIELAB L* (further transformed back to sRGB for consistent display).
Fig. 13b. CIELAB L* (further transformed back to sRGB for consistent display). Fig. 13c. Rec. 601 luma Y'.
Fig. 13c. Rec. 601 luma Y'.
 Fig. 13d. Component average: "intensity" I.
Fig. 13d. Component average: "intensity" I. Fig. 13e. HSV value V.
Fig. 13e. HSV value V. Fig. 13f. HSL lightness L.
Fig. 13f. HSL lightness L.
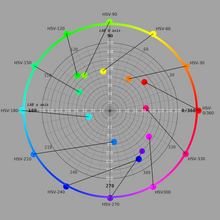
Though none of the dimensions in these spaces match their perceptual analogs, the value of HSV and the saturation of HSL are particular offenders. In HSV, the blue primary and white are held to have the same value, even though perceptually the blue primary has somewhere around 10% of the luminance of white (the exact fraction depends on the particular RGB primaries in use). In HSL, a mix of 100% red, 100% green, 90% blue – that is, a very light yellow – is held to have the same saturation as the green primary , even though the former color has almost no chroma or saturation by the conventional psychometric definitions. Such perversities led Cynthia Brewer, expert in color scheme choices for maps and information displays, to tell the American Statistical Association:
Computer science offers a few poorer cousins to these perceptual spaces that may also turn up in your software interface, such as HSV and HLS. They are easy mathematical transformations of RGB, and they seem to be perceptual systems because they make use of the hue–lightness/value–saturation terminology. But take a close look; don't be fooled. Perceptual color dimensions are poorly scaled by the color specifications that are provided in these and some other systems. For example, saturation and lightness are confounded, so a saturation scale may also contain a wide range of lightnesses (for example, it may progress from white to green which is a combination of both lightness and saturation). Likewise, hue and lightness are confounded so, for example, a saturated yellow and saturated blue may be designated as the same 'lightness' but have wide differences in perceived lightness. These flaws make the systems difficult to use to control the look of a color scheme in a systematic manner. If much tweaking is required to achieve the desired effect, the system offers little benefit over grappling with raw specifications in RGB or CMY.
If these problems make HSL and HSV problematic for choosing colors or color schemes, they make them much worse for image adjustment. HSL and HSV, as Brewer mentioned, confound perceptual color-making attributes, so that changing any dimension results in non-uniform changes to all three perceptual dimensions, and distorts all of the color relationships in the image. For instance, rotating the hue of a pure dark blue toward green will also reduce its perceived chroma, and increase its perceived lightness (the latter is grayer and lighter), but the same hue rotation will have the opposite impact on lightness and chroma of a lighter bluish-green – to (the latter is more colorful and slightly darker). In the example below (fig. 21), the image (a) is the original photograph of a green turtle. In the image (b), we have rotated the hue (H) of each color by −30°, while keeping HSV value and saturation or HSL lightness and saturation constant. In the image right (c), we make the same rotation to the HSL/HSV hue of each color, but then we force the CIELAB lightness (L*, a decent approximation of perceived lightness) to remain constant. Notice how the hue-shifted middle version without such a correction dramatically changes the perceived lightness relationships between colors in the image. In particular, the turtle's shell is much darker and has less contrast, and the background water is much lighter. Image (d) uses CIELAB to hue shift; the difference from (c) demonstrates the errors in hue and saturation.
 Fig. 21a. Color photograph.
Fig. 21a. Color photograph. Fig. 21b. HSL/HSV hue of each color shifted by −30°.
Fig. 21b. HSL/HSV hue of each color shifted by −30°. Fig. 21c. Hue shifted but CIELAB lightness (L*) kept as in the original.
Fig. 21c. Hue shifted but CIELAB lightness (L*) kept as in the original. Fig. 21d. Hue shifted in CIELch(ab) color space by −30°.
Fig. 21d. Hue shifted in CIELch(ab) color space by −30°.
Because hue is a circular quantity, represented numerically with a discontinuity at 360°, it is difficult to use in statistical computations or quantitative comparisons: analysis requires the use of circular statistics. Furthermore, hue is defined piecewise, in 60° chunks, where the relationship of lightness, value, and chroma to R, G, and B depends on the hue chunk in question. This definition introduces discontinuities, corners which can plainly be seen in horizontal slices of HSL or HSV.
Charles Poynton, digital video expert, lists the above problems with HSL and HSV in his Color FAQ, and concludes that:
HSB and HLS were developed to specify numerical Hue, Saturation and Brightness (or Hue, Lightness and Saturation) in an age when users had to specify colors numerically. The usual formulations of HSB and HLS are flawed with respect to the properties of color vision. Now that users can choose colors visually, or choose colors related to other media (such as PANTONE), or use perceptually-based systems like L*u*v* and L*a*b*, HSB and HLS should be abandoned.
Other cylindrical-coordinate color models
Main articles: Color model § Cylindrical-coordinate color models, and List of color spaces and their uses § Cylindrical transformationsThe creators of HSL and HSV were far from the first to imagine colors fitting into conic or spherical shapes, with neutrals running from black to white in a central axis, and hues corresponding to angles around that axis. Similar arrangements date back to the 18th century, and continue to be developed in the most modern and scientific models.
Color conversion formulae
To convert from HSL or HSV to RGB, we essentially invert the steps listed above (as before, R, G, B ∈ ). First, we compute chroma, by multiplying saturation by the maximum chroma for a given lightness or value. Next, we find the point on one of the bottom three faces of the RGB cube which has the same hue and chroma as our color (and therefore projects onto the same point in the chromaticity plane). Finally, we add equal amounts of R, G, and B to reach the proper lightness or value.
To RGB
HSL to RGB
Given a color with hue H ∈ , and lightness L ∈ , we first find chroma:
Then we can find a point (R1, G1, B1) along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value X for the second largest component of this color):
In the above equation, the notation refers to the remainder of the Euclidean division of by 2. is not necessarily an integer.
When is an integer, the "neighbouring" formula would yield the same result, as or , as appropriate.
Finally, we can find R, G, and B by adding the same amount to each component, to match lightness:
HSL to RGB alternative
The polygonal piecewise functions can be somewhat simplified by clever use of minimum and maximum values as well as the remainder operation.
Given a color with hue , saturation , and lightness , we first define the function:
where and:
And output R,G,B values (from ) are:
The above alternative formulas allow for shorter implementations. In the above formulas the operation also returns the fractional part of the module e.g. , and .
The base shape is constructed as follows: is a "triangle" for which values greater or equal to −1 start from k=2 and end at k=10, and the highest point is at k=6. Then by we change values bigger than 1 to equal 1. Then by we change values less than −1 to equal −1. At this point, we get something similar to the red shape from fig. 24 after a vertical flip (where the maximum is 1 and the minimum is −1). The R,G,B functions of use this shape transformed in the following way: modulo-shifted on (by ) (differently for R,G,B) scaled on (by ) and shifted on (by ).
We observe the following shape properties (Fig. 24 can help to get an intuition about them):
HSV to RGB
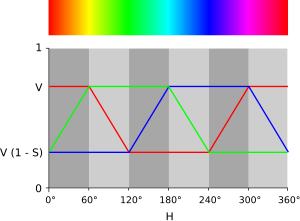
Given an HSV color with hue H ∈ , and value V ∈ , we can use the same strategy. First, we find chroma:
Then we can, again, find a point (R1, G1, B1) along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value X for the second largest component of this color):
As before, when is an integer, "neighbouring" formulas would yield the same result.
Finally, we can find R, G, and B by adding the same amount to each component, to match value:
HSV to RGB alternative
Given a color with hue , saturation , and value , first we define function :
where and:
And output R,G,B values (from ) are:
Above alternative equivalent formulas allow shorter implementation. In above formulas the returns also fractional part of module e.g. the formula . The values of . The base shape
is constructed as follows: is "triangle" for which non-negative values starts from k=0, highest point at k=2 and "ends" at k=4, then we change values bigger than one to one by , then change negative values to zero by – and we get (for ) something similar to green shape from Fig. 24 (which max value is 1 and min value is 0). The R,G,B functions of use this shape transformed in following way: modulo-shifted on (by ) (differently for R,G,B) scaled on (by ) and shifted on (by ). We observe following shape properties(Fig. 24 can help to get intuition about this):
HSI to RGB
Given an HSI color with hue H ∈ , and intensity I ∈ , we can use the same strategy, in a slightly different order:
Where is the chroma.
Then we can, again, find a point (R1, G1, B1) along the bottom three faces of the RGB cube, with the same hue and chroma as our color (using the intermediate value X for the second largest component of this color):
Overlap (when is an integer) occurs because two ways to calculate the value are equivalent: or , as appropriate.
Finally, we can find R, G, and B by adding the same amount to each component, to match lightness:
Luma, chroma and hue to RGB
Given a color with hue H ∈ , and luma Y′601 ∈ , we can again use the same strategy. Since we already have H and C, we can straightaway find our point (R1, G1, B1) along the bottom three faces of the RGB cube:
Overlap (when is an integer) occurs because two ways to calculate the value are equivalent: or , as appropriate.
Then we can find R, G, and B by adding the same amount to each component, to match luma:
Interconversion
HSV to HSL
Given a color with hue
HSL to HSV
Given a color with hue
From RGB
This is a reiteration of the previous conversion.
Value must be in range .
With maximum component (i. e. value)
and minimum component
- ,
range (i. e. chroma)
and mid-range (i. e. lightness)
- ,
we get common hue:
and distinct saturations:
Swatches
Mouse over the swatches below to see the R, G, and B values for each swatch in a tooltip.
HSL
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
HSV
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
See also
Notes
- In the Joblove and Greenberg (1978) paper first introducing HSL, they called HSL lightness "intensity", called HSL saturation "relative chroma", called HSV saturation "saturation" and called HSV value "value". They carefully and unambiguously described and compared three models: hue/chroma/intensity, hue/relative chroma/intensity, and hue/value/saturation. Unfortunately, later authors were less fastidious, and current usage of these terms is inconsistent and often misleading.
- The name hexcone for hexagonal pyramid was coined in Smith (1978), and stuck.
- For instance, a 1982 study by Berk, et al., found that users were better at describing colors in terms of HSL than RGB coordinates, after being taught both systems, but were much better still at describing them in terms of the natural-language CNS model (which uses names such as "very dark grayish yellow-green" or "medium strong bluish purple"). This shouldn't be taken as gospel however: a 1987 study by Schwarz, et al., found that users could match colors using RGB controls faster than with HSL controls; a 1999 study by Douglas and Kirkpatrick found that the visual feedback in the user interface mattered more than the particular color model in use, for user matching speed.
- "Clearly, if color appearance is to be described in a systematic, mathematical way, definitions of the phenomena being described need to be precise and universally agreed upon."
- In Levkowitz and Herman's formulation, R, G, and B stand for the voltages on the guns of a CRT display, which might have different maxima, and so their cartesian gamut could be a box of any unequal dimensions. Other definitions commonly use integer values in the range , storing the value for each component in one byte. We define the RGB gamut to be a unit cube for convenience because it simplifies and clarifies the math. Also, in general, HSL and HSV are today computed directly from gamma-corrected R′, G′, and B′ – for instance in sRGB space – but, when the models were developed, might have been transformations of a linear RGB space. Early authors don't address gamma correction at all, except Alvy Ray Smith who clearly states that "We shall assume that an RGB monitor is a linear device", and thus designed HSV using linear RGB. We will drop the primes, and the labels R, G, and B should be taken to stand for the three attributes of the origin RGB space, whether or not it is gamma corrected.
- Using the chroma here not only agrees with the original Joblove and Greenberg (1978) paper, but is also in the proper spirit of the psychometric definition of the term. Some models call this attribute saturation – for instance Adobe Photoshop's "Saturation" blend mode – but such use is even more confusing than the use of the term in HSL or HSV, especially when two substantially different definitions are used side by side.
- ^ Most of the computer graphics papers and books discussing HSL or HSV have a formula or algorithm describing them formally. Our formulas which follow are some mix of those. See, for instance, Agoston (2005) or Foley (1995)
- Hanbury and Serra (2002) put a great deal of effort into explaining why what we call chroma here can be written as max(R, G, B) − min(R, G, B), and showing that this value is a seminorm. They reserve the name chroma for the Euclidean norm in the chromaticity plane (our C2), and call this hexagonal distance saturation instead, as part of their IHLS model
- In the following, the multiplication of hue by 60° – that is, 360°/6 – can be seen as the hexagonal-geometry analogue of the conversion from radians to degrees, a multiplication by 360°/2π: the circumference of a unit circle is 2π; the circumference of a unit hexagon is 6.
- For a more specific discussion of the term luma, see Charles Poynton (2008). See also RGB color space#Specifications. Photoshop exclusively uses the NTSC coefficients for its "Luminosity" blend mode regardless of the RGB color space involved.
- The first nine colors in this table were chosen by hand, and the last ten colors were chosen at random.
- See Smith (1978). Many of these screenshots were taken from the GUIdebook, and the rest were gathered from image search results.
- For instance, a tool in Illustrator CS4, and Adobe's related web tool, Kuler, both allow users to define color schemes based on HSV relationships, but with a hue circle modified to better match the RYB model used traditionally by painters. The web tools ColorJack, Color Wizard, and ColorBlender all pick color schemes with reference to HSL or HSV.
- Try a web search for " color picker" for examples for a given framework, or "JavaScript color picker" for general results.
- ArcGIS calls its map-symbol gradients "color ramps". Current versions of ArcGIS can use CIELAB instead for defining them.
- For instance, the first version of Photoshop had an HSL-based tool; see "Photoshop hue/saturation" in the GUIdebook for screenshots.
- Photoshop's documentation explains that, e.g., "Luminosity: Creates a result color with the hue and saturation of the base color and the luminance of the blend color."
- The HSL-style mode (with a Rec. 601 Luminosity) are also standardized in CSS from a documentation contributed by Adobe and Canon. GIMP 2.10 has switched to LCH(ab) from its older HSV geometry.
- The Ohta et al. model has parameters I1 = (R + G + B)/3, I2 = (R − B)/2, I3 = (2G − R − B)/4. I1 is the same as our I, and I2 and I3 are similar to our β and α, respectively, except that (a) where α points in the direction of R in the "chromaticity plane", I3 points in the direction of G, and (b) the parameters have a different linear scaling which avoids the √3 of our β.
- Most of the disadvantages below are listed in Poynton (1997), though as mere statements, without examples.
- Some points in this cylinder fall out of gamut.
References
- See Absolute color space.
- ^ Levkowitz and Herman (1993)
- Wilhelm Ostwald (1916). Die Farbenfibel. Leipzig.
- Wilhelm Ostwald (1918). Die Harmonie der Farben. Leipzig.
- US patent 4694286, Bergstedt, Gar A., "Apparatus and method for modifying displayed color images", published 1987-09-15, assigned to Tektronix, Inc
- Toby Berk; Arie Kaufman; Lee Brownston (August 1982). "A human factors study of color notation systems for computer graphics". Communications of the ACM. 25 (8): 547–550. doi:10.1145/358589.358606. S2CID 14838329.
- Michael W. Schwarz; William B. Cowan; John C. Beatty (April 1987). "An experimental comparison of RGB, YIQ, LAB, HSV, and opponent color models". ACM Transactions on Graphics. 6 (2): 123–158. doi:10.1145/31336.31338. S2CID 17287484.
- Sarah A. Douglas; Arthur E. Kirkpatrick (April 1999). "Model and representation: the effect of visual feedback on human performance in a color picker interface". ACM Transactions on Graphics. 18 (2): 96–127. doi:10.1145/318009.318011. S2CID 14678328.
- The original patent on this idea was by Georges Valensi in 1938: FR patent 841335, Valensi, Georges, "Procédé de télévision en couleurs", published 1939-05-17, issued 1939-02-06 US patent 2375966, Valensi, Georges, "System of television in colors", published 1945-05-15
- ^ Smith (1978)
- ^ Joblove and Greenberg (1978)
- Maureen C. Stone (August 2001). "A Survey of Color for Computer Graphics". Course at SIGGRAPH 2001.
- Ware Myers (July 1979). "Interactive Computer Graphics: Flying High-Part I". Computer. 12 (7): 8–17. doi:10.1109/MC.1979.1658808. S2CID 15344162.
- N. Magnetat-Thalmann; N. Chourot; D. Thalmann (March 1984). "Colour Gradation, Shading and Texture Using a Limited Terminal". Computer Graphics Forum. 3: 83–90. doi:10.1111/j.1467-8659.1984.tb00092.x. S2CID 29541525.
- Computer Graphics Staff (August 1979). "Status report of the graphic standards planning committee". ACM SIGGRAPH Computer Graphics. 13 (3): 1–10. doi:10.1145/988497.988498. S2CID 43687764.
- ^ Fairchild (2005), pp. 83–93
- Kuehni (2003)
- Standard Terminology of Appearance E284. ASTM. 2009.
- International Lighting Vocabulary (4th ed.). CIE and IEC. 1987. ISBN 978-3-900734-07-7. Archived from the original on 2010-02-27. Retrieved 2010-02-05.
- Poynton (1997)
- Sharma, G. (2003). Digital Color Imaging Handbook. Boca Raton, FL: CRC Press. ISBN 978-0-8493-0900-7.
- Hanbury and Serra (2002)
- ^ Hanbury (2008)
- Patrick Lambert; Thierry Carron (1999). "Symbolic fusion of luminance-hue-chroma features for region segmentation". Pattern Recognition. 32 (11): 1857. Bibcode:1999PatRe..32.1857L. doi:10.1016/S0031-3203(99)00010-2.
- Rafael C. Gonzalez and Richard Eugene Woods (2008). Digital Image Processing, 3rd ed. Upper Saddle River, NJ: Prentice Hall. ISBN 0-13-168728-X. pp. 407–413.
- Poynton (1997). "What weighting of red, green and blue corresponds to brightness?"
- Bruce Lindbloom (2001-09-25). http://lists.apple.com/archives/colorsync-users/2001/Sep/msg00488.html Archived 2011-07-07 at the Wayback Machine "Re: Luminosity channel...".
- ^ Cheng et al. (2001)
- Tantek Çelik, Chris Lilley, and L. David Baron (July 2008). "CSS3 Color Module Level 3".
- "Working with color ramps". Environmental Systems Research Institute. January 2008. Retrieved August 30, 2017.
- Bradley, John (1994). "The HSV Modification Tools". John's World of XV and Other Cool Stuff.
- Sinkel, Kiril (January 2010). "User Guide for Picture Window and Picture Window Pro Digital Light & Color" (PDF). Archived from the original (PDF) on 2014-05-12.
- "Blending Modes". Photoshop User Guide. Adobe Systems Incorporated. February 15, 2017.
- "Compositing and Blending Level 1". www.w3.org.
- "GIMP's LCH Blend Modes". Nine Degrees Below.
- John Kender (1976). "Saturation, hue and normalized color". Carnegie Mellon University, Computer Science Dept. Pittsburgh, PA.
- Yu-Ichi Ohta; Takeo Kanade; Toshiyuki Sakai (1980). "Color information for region segmentation". Computer Graphics and Image Processing. 13 (3): 222. doi:10.1016/0146-664X(80)90047-7.
- Ffrank Perez; Christof Koch (1994). "Toward color image segmentation in analog VLSI: Algorithm and hardware" (PDF). International Journal of Computer Vision. 12: 17–42. doi:10.1007/BF01420983. S2CID 6140819.
- Brewer, Cynthia A. (1999). "Color Use Guidelines for Data Representation". Proceedings of the Section on Statistical Graphics. Alexandria, VA: American Statistical Association. pp. 55–60. Archived from the original on 2009-08-07. Retrieved 2010-02-05.
- Fisher, Nicholas (1993). Statistical Analysis of Circular Dat. Cambridge University Press. doi:10.1017/CBO9780511564345. ISBN 978-0-521-35018-1.
- Hanbury, Allan (2003). Circular Statistics Applied to Colour Images. 8th Computer Vision Winter Workshop. CiteSeerX 10.1.1.4.1381.
- Poynton (1997). "What are HSB and HLS?"
Bibliography
- Agoston, Max K. (2005). Computer Graphics and Geometric Modeling: Implementation and Algorithms. London: Springer. pp. 300–306. ISBN 978-1-85233-818-3. Agoston's book contains a description of HSV and HSL, and algorithms in pseudocode for converting to each from RGB, and back again.
- Cheng, Heng-Da; Jiang, Xihua; Sun, Angela; Wang, Jingli (2001). "Color image segmentation: Advances and prospects". Pattern Recognition. 34 (12): 2259. Bibcode:2001PatRe..34.2259C. CiteSeerX 10.1.1.119.2886. doi:10.1016/S0031-3203(00)00149-7. S2CID 205904573. This computer vision literature review briefly summarizes research in color image segmentation, including that using HSV and HSI representations.
- Fairchild, Mark D. (2005). Color Appearance Models (2nd ed.). Addison-Wesley. This book doesn't discuss HSL or HSV specifically, but is one of the most readable and precise resources about current color science.
- Foley, J. D.; et al. (1995). Computer Graphics: Principles and Practice (2nd ed.). Redwood City, CA: Addison-Wesley. ISBN 978-0-201-84840-3. The standard computer graphics textbook of the 1990s, this tome has a chapter full of algorithms for converting between color models, in C.
- Hanbury, Allan; Serra, Jean (December 2002). A 3D-polar Coordinate Colour Representation Suitable for Image Analysis. Vienna, Austria: Vienna University of Technology.
{{cite book}}:|work=ignored (help) - Hanbury, Allan (2008). "Constructing cylindrical coordinate colour spaces" (PDF). Pattern Recognition Letters. 29 (4): 494–500. Bibcode:2008PaReL..29..494H. CiteSeerX 10.1.1.211.6425. doi:10.1016/j.patrec.2007.11.002.
- Joblove, George H.; Greenberg, Donald (August 1978). "Color spaces for computer graphics" (PDF). Computer Graphics. 12 (3): 20–25. doi:10.1145/965139.807362. Joblove and Greenberg's paper was the first describing the HSL model, which it compares to HSV.
- Kuehni, Rolf G. (2003). Color Space and Its Divisions: Color Order from Antiquity to the present. New York: Wiley. ISBN 978-0-471-32670-0. This book only briefly mentions HSL and HSV, but is a comprehensive description of color order systems through history.
- Levkowitz, Haim; Herman, Gabor T. (1993). "GLHS: A Generalized Lightness, Hue and Saturation Color Model". CVGIP: Graphical Models and Image Processing. 55 (4): 271–285. doi:10.1006/cgip.1993.1019. This paper explains how both HSL and HSV, as well as other similar models, can be thought of as specific variants of a more general "GLHS" model. Levkowitz and Herman provide pseudocode for converting from RGB to GLHS and back.
- MacEvoy, Bruce (January 2010). "Color Vision". handprint.com.. Especially the sections about "Modern Color Models" and "Modern Color Theory". MacEvoy's extensive site about color science and paint mixing is one of the best resources on the web. On this page, he explains the color-making attributes, and the general goals and history of color order systems – including HSL and HSV – and their practical relevance to painters.
- Poynton, Charles (1997). "Frequently Asked Questions About Color". poynton.com. This self-published frequently asked questions page, by digital video expert Charles Poynton, explains, among other things, why in his opinion these models "are useless for the specification of accurate color", and should be abandoned in favor of more psychometrically relevant models.
- Poynton, Charles (2008). "YUV and luminance considered harmful". poynton.com. Retrieved August 30, 2017.
- Smith, Alvy Ray (August 1978). "Color gamut transform pairs". Computer Graphics. 12 (3): 12–19. doi:10.1145/965139.807361. This is the original paper describing the "hexcone" model, HSV. Smith was a researcher at NYIT's Computer Graphics Lab. He describes HSV's use in an early digital painting program.
External links
- Demonstrative color conversion applet
- HSV Colors by Hector Zenil, The Wolfram Demonstrations Project.
- HSV to RGB by CodeBeautify.
| Color space | |
|---|---|
| CAM | |
| CIE | |
| RGB | |
| Y′UV | |
| Other | |
| Color systems and standards | |
| For the vision capacities of organisms or machines, see | |









 a difference of about 13.4%.
a difference of about 13.4%.



 (SDTV)
(SDTV)








 refers to the remainder of the
refers to the remainder of the  by 2.
by 2. 
 or
or  , as appropriate.
, as appropriate.


 , saturation
, saturation  , and lightness
, and lightness  , we first define the function:
, we first define the function:

 and:
and:


 ) are:
) are:

 operation also returns the fractional part of the module e.g.
operation also returns the fractional part of the module e.g.  , and
, and  .
.
 is constructed as follows:
is constructed as follows:  is a "triangle" for which values greater or equal to −1 start from k=2 and end at k=10, and the highest point is at k=6. Then by
is a "triangle" for which values greater or equal to −1 start from k=2 and end at k=10, and the highest point is at k=6. Then by  we change values bigger than 1 to equal 1. Then by
we change values bigger than 1 to equal 1. Then by  we change values less than −1 to equal −1. At this point, we get something similar to the red shape from fig. 24 after a vertical flip (where the maximum is 1 and the minimum is −1). The R,G,B functions of
we change values less than −1 to equal −1. At this point, we get something similar to the red shape from fig. 24 after a vertical flip (where the maximum is 1 and the minimum is −1). The R,G,B functions of  use this shape transformed in the following way: modulo-shifted on
use this shape transformed in the following way: modulo-shifted on  (by
(by  ) (differently for R,G,B) scaled on
) (differently for R,G,B) scaled on  (by
(by  ) and shifted on
) and shifted on  ).
).



 shows origin of marked vertical axis values.
shows origin of marked vertical axis values.


 , and value
, and value  , first we define function :
, first we define function :



 . The base shape
. The base shape

 is "triangle" for which non-negative values starts from k=0, highest point at k=2 and "ends" at k=4, then we change values bigger than one to one by
is "triangle" for which non-negative values starts from k=0, highest point at k=2 and "ends" at k=4, then we change values bigger than one to one by  , then change negative values to zero by
, then change negative values to zero by  – and we get (for
– and we get (for  ) something similar to green shape from Fig. 24 (which max value is 1 and min value is 0). The R,G,B functions of
) something similar to green shape from Fig. 24 (which max value is 1 and min value is 0). The R,G,B functions of  ) and shifted on
) and shifted on  ). We observe following shape properties(Fig. 24 can help to get intuition about this):
). We observe following shape properties(Fig. 24 can help to get intuition about this):






 is the chroma.
is the chroma.





 , and value
, and value 



 , and luminance
, and luminance 


 .
.

 ,
,
 ,
,

