| Revision as of 04:39, 4 November 2010 view sourceIxfd64 (talk | contribs)Edit filter managers, Administrators69,961 editsm Reverted edits by 203.26.13.2 (talk) to last revision by Hans Adler (HG)← Previous edit | Latest revision as of 02:48, 6 January 2025 view source David Eppstein (talk | contribs)Autopatrolled, Administrators227,077 edits David E. Joyce (mathematician) | ||
| Line 1: | Line 1: | ||
| {{Short description|Relation between sides of a right triangle}} | |||
| {{See also|Pythagorean trigonometric identity}} | |||
| {{pp-move-indef|small=yes}} | |||
| ]{{Trigonometry}} | |||
| {{pp-semi-indef}} | |||
| In ], the '''Pythagorean theorem''' or '''Pythagoras' theorem''' is a relation in ] among the three sides of a ] (''right-angled triangle''). In terms of areas, it states: | |||
| {{Infobox mathematical statement | |||
| <blockquote> | |||
| | name = Pythagorean theorem | |||
| In any right triangle, the area of the square whose side is the ] (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a ]). | |||
| | image = Pythagorean.svg | |||
| </blockquote> | |||
| | caption = | |||
| The ] can be written as an ] relating the lengths of the sides ''a'', ''b'' and ''c'', often called the ''Pythagorean equation'':<ref name=Sally0> | |||
| | type = ] | |||
| | field = ] | |||
| | statement = The sum of the areas of the two squares on the legs (''a'' and ''b'') equals the area of the square on the hypotenuse (''c''). | |||
| | symbolic statement = <math>a^2 + b^2 = c^2</math> | |||
| | generalizations = {{Plainlist| | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| }} | |||
| | consequences = {{Plainlist| | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| * ] | |||
| }} | |||
| }} | |||
| {{General geometry |concepts}} | |||
| In ], the '''Pythagorean theorem''' or '''Pythagoras' theorem''' is a fundamental relation in ] between the three sides of a ]. It states that the area of the ] whose side is the ] (the side opposite the ]) is equal to the sum of the areas of the squares on the other two sides. | |||
| {{cite book |title=Roots to research: a vertical development of mathematical problems |author=Judith D. Sally, Paul Sally |page=63 |chapter=Chapter 3: Pythagorean triples |url=http://books.google.com/books?id=nHxBw-WlECUC&pg=PA63 | |||
| |isbn=0821844032 |year=2007 |publisher=American Mathematical Society Bookstore}} | |||
| </ref> | |||
| :<math>a^2 + b^2 = c^2\!\,</math> | |||
| where ''c'' represents the length of the hypotenuse, and ''a'' and ''b'' represent the lengths of the other two sides. | |||
| The ] can be written as an ] relating the lengths of the sides {{mvar|a}}, {{mvar|b}} and the hypotenuse {{mvar|c}}, sometimes called the '''Pythagorean equation''':<ref name="Sally0">{{cite book |title=Roots to research: a vertical development of mathematical problems |author1=Judith D. Sally |author2=Paul Sally |page=63 |chapter=Chapter 3: Pythagorean triples |chapter-url=https://books.google.com/books?id=nHxBw-WlECUC&pg=PA63 |isbn=978-0-8218-4403-8 |year=2007 |publisher=American Mathematical Society Bookstore}}</ref> | |||
| These two formulations show two fundamental aspects of this theorem: it is both a statement about ''areas'' and about ''lengths''. ] refers to these as ''areal'' and ''metric'' interpretations.<ref name=Dantzig> | |||
| :<math>a^2 + b^2 = c^2 .</math> | |||
| The theorem is named for the ] philosopher ], born around 570 BC. The theorem has been ] numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both ] proofs and ] proofs, with some dating back thousands of years. | |||
| When ] is represented by a ] in ], ] satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points. | |||
| {{cite book |title=The bequest of the Greeks |author=Tobias Dantzig |year=1955 |page=97 |publisher=Charles Scribner's Sons |url=http://books.google.com/?id=nSg4AAAAMAAJ&cd=1&dq=bibliogroup%3A%22Mathematics+in+retrospect%22&q=not+as+a+metric#search_anchor}} | |||
| The theorem can be ] in various ways: to ]s, to ], to objects that are not right triangles, and to objects that are not triangles at all but ] solids. | |||
| </ref><ref>{{Harv|Maor|2007|p=39}}</ref> Some proofs of the theorem are based on one interpretation, some upon the other. Thus, Pythagoras' theorem stands with one foot in geometry and the other in algebra, a connection made clear originally by ] in his work ], and extending today into other branches of mathematics.<ref name=Allman> | |||
| ==Proofs using constructed squares== | |||
| {{cite book |title=The Encyclopaedia Britannica: A Dictionary of Arts, Sciences, and General Literature, Volume 20 |publisher=H.G. Allen |editor=Thomas Spencer Baynes |url=http://books.google.com/books?id=C84MAAAAYAAJ&pg=PA142 |page=142 |author=GJ Allman |year=1888 |edition=9th}} | |||
| ] | |||
| </ref> | |||
| === Rearrangement proofs === | |||
| The Pythagorean theorem has been modified to apply outside its original domain. A number of these generalizations are described below, including extension to many-dimensional Euclidean spaces, to spaces that are not Euclidean, to objects that are not right triangles, and indeed, to objects that are not triangles at all, but ''n''-dimensional solids. | |||
| In one rearrangement proof, two squares are used whose sides have a measure of <math>a + b</math> and which contain four right triangles whose sides are {{mvar|a}}, {{mvar|b}} and {{mvar|c}}, with the hypotenuse being {{mvar|c}}. In the square on the right side, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length {{mvar|c}}. Each outer square has an area of <math>(a+b)^2</math> as well as <math>2ab + c^2</math>, with <math>2ab</math> representing the total area of the four triangles. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length {{mvar|a}} and {{mvar|b}}. These rectangles in their new position have now delineated two new squares, one having side length {{mvar|a}} is formed in the bottom-left corner, and another square of side length {{mvar|b}} formed in the top-right corner. In this new position, this left side now has a square of area <math>(a+b)^2</math> as well as <math>2ab + a^2 + b^2 </math>] Since both squares have the area of <math>(a+b)^2</math> it follows that the other measure of the square area also equal each other such that <math>2ab + c^2</math> = <math>2ab + a^2 + b^2 </math>. With the area of the four triangles removed from both side of the equation what remains is <math>a^2 + b^2 = c^2 .</math> <ref>Benson, Donald. '''', pp. 172–173 (Oxford University Press, 1999).</ref> | |||
| In another proof rectangles in the second box can also be placed such that both have one corner that correspond to consecutive corners of the square. In this way they also form two boxes, this time in consecutive corners, with areas <math> a^2 </math> and <math> b^2 </math>which will again lead to a second square of with the area <math>2ab + a^2 + b^2 </math>. | |||
| The Pythagorean theorem is named after the ] ] ], who by tradition is credited with its discovery and ],<ref name=Allman2> | |||
| English mathematician ] gives this proof in his commentary on Proposition I.47 in ] '']'', and mentions the proposals of German mathematicians ] and ] that Pythagoras may have known this proof. Heath himself favors a different proposal for a Pythagorean proof, but acknowledges from the outset of his discussion "that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him."<ref>{{harvtxt|Euclid|1956}}, pp. 351–352</ref> Recent scholarship has cast increasing doubt on any sort of role for Pythagoras as a creator of mathematics, although debate about this continues.<ref>{{cite encyclopedia |title=Pythagoras |encyclopedia=The Stanford Encyclopedia of Philosophy (Winter 2018 Edition) |url=https://plato.stanford.edu/archives/win2018/entries/pythagoras/ |last=Huffman |first=Carl |date=23 February 2005 |editor-last=Zalta |editor-first=Edward N. |editor-link=Edward N. Zalta}}, "It should now be clear that decisions about sources are crucial in addressing the question of whether Pythagoras was a mathematician and scientist. The view of Pythagoras's cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus."</ref> | |||
| {{cite book |title=Greek Geometry from Thales to Euclid |author=George Johnston Allman |page=26 |url=http://books.google.com/?id=-gYCAAAAYAAJ&pg=PA26 |publisher=Hodges, Figgis, & Co |year=1889 |quote=The discovery of the law of three squares, commonly called the "theorem of Pythagoras" is attributed to him by – amongst others – Vitruvius, Diogenes Laertius, Proclus, and Plutarch ... |edition=Reprinted by Kessinger Publishing LLC 2005 |isbn=143260662X}} | |||
| === Algebraic proofs === | |||
| </ref><ref name="heath144">{{Harv|Heath|1921|loc= Vol I, p. 144}}</ref> although it is often argued that knowledge of the theorem predates him. (There is much evidence that ] understood the formula, although there is little surviving evidence that they fitted it into a mathematical framework.<ref name=Neugebauer> | |||
| ] | |||
| The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side {{mvar|c}}, as shown in the lower part of the diagram.<ref>{{cite web |author=Alexander Bogomolny |title=Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4 |url=http://www.cut-the-knot.org/pythagoras/index.shtml#4 |access-date=4 November 2010 |work=Cut the Knot}}</ref> This results in a larger square, with side {{math|''a'' + ''b''}} and area {{math|(''a'' + ''b'')<sup>2</sup>}}. The four triangles and the square side {{mvar|c}} must have the same area as the larger square, | |||
| :<math>(b+a)^2 = c^2 + 4\frac{ab}{2} = c^2+2ab,</math> | |||
| giving | |||
| {{cite book |title=The exact sciences in antiquity |page=36 |url=http://books.google.com/?id=JVhTtVA2zr8C&pg=PA36 | |||
| |author=Otto Neugebauer |isbn=0486223329 |year=1969 |edition=Republication of 1957 Brown University Press 2nd |publisher=Courier Dover Publications}}. For a different view, see {{cite book |author=Dick Teresi |page =52 |title=Lost Discoveries: The Ancient Roots of Modern Science |url=http://books.google.com/?id=pheL_ubbXD0C&pg=PA52 |isbn=074324379X |year=2003 |publisher=Simon and Schuster}}, where the speculation is made that the first column of a tablet 322 in the ] supports a Babylonian knowledge of some elements of trigonometry. That notion is pretty much laid to rest by {{cite journal |author=Eleanor Robson |title=Words and Pictures: New Light on Plimpton 322 |year=2002 |doi= 10.2307/2695324|url=http://www.jstor.org/stable/2695324 |journal=The American Mathematical Monthly |volume=109 |issue=2 |pages=105–120 |publisher=Mathematical Association of America |ref=harv}} See also . The accepted view today is that the Babylonians had no awareness of trigonometric functions. See {{cite journal |title=The Plimpton 322 Tablet and the Babylonian Method of Generating Pythagorean Triples |author=Abdulrahman A. Abdulaziz |year=2010 |url=http://arxiv.org/abs/1004.0025v1 |journal=ArXiv preprint |ref=harv }} §2, page 7. | |||
| :<math>c^2 = (b+a)^2 - 2ab = b^2+2ab+a^2-2ab = a^2 + b^2.</math> | |||
| </ref>) " mathematics provided practical tools in the form of 'recipes' designed for specific calculations. Pythagoras, on the other hand, was one of the first to grasp numbers as abstract entities that exist in their own right."<ref name=Livio> | |||
| A similar proof uses four copies of a right triangle with sides {{mvar|a}}, {{mvar|b}} and {{mvar|c}}, arranged inside a square with side {{mvar|c}} as in the top half of the diagram.<ref name="rotate"> | |||
| {{cite web |author=Alexander Bogomolny |title=Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3 |url=http://www.cut-the-knot.org/pythagoras/index.shtml#3 |access-date=4 November 2010 |work=Cut the Knot}} | |||
| </ref> The triangles are similar with area <math>\tfrac12ab</math>, while the small square has side {{math|''b'' − ''a''}} and area {{math|(''b'' − ''a'')<sup>2</sup>}}. The area of the large square is therefore | |||
| :<math>(b-a)^2+4\frac{ab}{2} = (b-a)^2+2ab = b^2-2ab+a^2+2ab = a^2+b^2. </math> | |||
| But this is a square with side {{mvar|c}} and area {{math|''c''<sup>2</sup>}}, so | |||
| {{cite book |title=The golden ratio: the story of phi, the world's most astonishing number |author= Mario Livio |page=25 |url=http://books.google.com/?id=bUARfgWRH14C&pg=PA25 |isbn=0767908163 |publisher=Random House, Inc |year=2003 }} | |||
| </ref> | |||
| :<math>c^2 = a^2 + b^2. </math> | |||
| The Pythagorean theorem has attracted interest outside mathematics as a symbol of mathematical abstruseness, mystique, or intellectual power. Popular references to Pythagoras' theorem in literature, plays, musicals, songs, stamps and cartoons abound. | |||
| : | |||
| ==Other forms== | |||
| As pointed out in the introduction, if ''c'' denotes the ] of the hypotenuse and ''a'' and ''b'' denote the lengths of the other two sides, Pythagoras' theorem can be expressed as the Pythagorean equation: | |||
| ==Other proofs of the theorem== | |||
| : <math>a^2 + b^2 = c^2\, </math> | |||
| This theorem may have more known proofs than any other (the ] of ] being another contender for that distinction); the book ''The Pythagorean Proposition'' contains 370 proofs.<ref>{{Harv|Loomis|1940}}</ref> | |||
| or, solved for ''c'': | |||
| : <math> c = \sqrt{a^2 + b^2}. \,</math> | |||
| If ''c'' is known, and the length of one of the legs must be found, the following equations can be used: | |||
| : <math>b = \sqrt{c^2 - a^2}. \,</math> | |||
| or | |||
| : <math>a = \sqrt{c^2 - b^2}. \,</math> | |||
| The Pythagorean equation provides a simple relation among the three sides of a right triangle so that if the lengths of any two sides are known, the length of the third side can be found. A generalization of this theorem is the ], which allows the computation of the length of the third side of any triangle, given the lengths of two sides and the size of the angle between them. If the angle between the sides is a right angle, the law of cosines reduces to the Pythagorean equation. | |||
| ==Proofs== | |||
| This theorem may have more known proofs than any other (the law of ] being another contender for that distinction); the book ''The Pythagorean Proposition'' contains 370 proofs.<ref>{{Harv|Loomis|1968}}</ref> | |||
| ===Proof using similar triangles=== | ===Proof using similar triangles=== | ||
| ] | |||
| This proof is based on the ] of the sides of two ] triangles, that is, upon the fact that the ] of any two corresponding sides of similar triangles is the same regardless of the size of the triangles. | |||
| {{hatnote|In this section, and as usual in geometry, a "word" of two capital letters, such as {{mvar|AB}} denotes the length of the ] defined by the points labeled with the letters, and not a multiplication. So, {{math|''AB''{{sup|2}}}} denotes the square of the length {{mvar|AB}} and not the product <math>A\times B^2.</math>}} | |||
| Let ''ABC'' represent a right triangle, with the right angle located at ''C'', as shown on the figure. We draw the ] from point ''C'', and call ''H'' its intersection with the side ''AB''. Point ''H'' divides the length of the hypotenuse ''c'' into parts ''d'' and ''e''. The new triangle ''ACH'' is ] to triangle ''ABC'', because they both have a right angle (by definition of the altitude), and they share the angle at ''A'', meaning that the third angle will be the same in both triangles as well, marked as ''θ'' in the figure. By a similar reasoning, the triangle ''CBH'' is also similar to ''ABC''. The proof of similarity of the triangles requires the ]: the sum of the angles in a triangle is two right angles, and is equivalent to the ]. Similarity of the triangles leads to the equality of ratios of corresponding sides: | |||
| ] | |||
| This proof is based on the ] of the sides of three ] triangles, that is, upon the fact that the ] of any two corresponding sides of similar triangles is the same regardless of the size of the triangles. | |||
| Let ''ABC'' represent a right triangle, with the ] located at {{mvar|C}}, as shown on the figure. Draw the ] from point {{mvar|C}}, and call {{mvar|H}} its intersection with the side ''AB''. Point {{mvar|H}} divides the length of the hypotenuse {{mvar|c}} into parts {{mvar|d}} and {{mvar|e}}. The new triangle, ''ACH,'' is ] to triangle ''ABC'', because they both have a right angle (by definition of the altitude), and they share the angle at {{mvar|A}}, meaning that the third angle will be the same in both triangles as well, marked as {{mvar|θ}} in the figure. By a similar reasoning, the triangle ''CBH'' is also similar to ''ABC''. The proof of similarity of the triangles requires the ]: The sum of the angles in a triangle is two right angles, and is equivalent to the ]. Similarity of the triangles leads to the equality of ratios of corresponding sides: | |||
| :<math> \frac{a}{c}=\frac{e}{a} \mbox{ and } \frac{b}{c}=\frac{d}{b}.\,</math> | |||
| :<math> \frac{BC}{AB}=\frac{BH}{BC} \text{ and }\frac{AC}{AB}=\frac{AH}{AC}.</math> | |||
| The first result equates the ]s of the angles {{mvar|θ}}, whereas the second result equates their ]s. | |||
| These ratios can be written as | |||
| The first result equates the ] of each angle ''θ'' and the second result equates the ]s. | |||
| :<math>BC^2=AB\times BH\text{ and } AC^2=AB\times AH. </math> | |||
| Summing these two equalities results in | |||
| :<math>BC^2+AC^2=AB\times BH+AB\times AH=AB(AH+BH)=AB^2 ,</math> | |||
| which, after simplification, demonstrates the Pythagorean theorem: | |||
| :<math>BC^2+AC^2=AB^2.</math> | |||
| The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One ] is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the ''Elements'', and that the theory of proportions needed further development at that time.<ref>{{Harv|Maor|2007| p= }}</ref> | |||
| These ratios can be written as: | |||
| :<math>a^2=c\times e \mbox{ and }b^2=c\times d. \,</math> | |||
| Summing these two equalities, we obtain | |||
| :<math>a^2+b^2=c\times e+c\times d=c\times(d+e)=c^2 ,\,\!</math> | |||
| which, tidying up, is the Pythagorean theorem: | |||
| :<math>a^2+b^2=c^2 \ .\,\!</math> | |||
| ===Einstein's proof by dissection without rearrangement=== | |||
| This is a ''metric'' proof in the sense of Dantzig, one that depends on lengths, not areas. The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the ''Elements'', and that the theory of proportions needed further development at that time.<ref>{{Harv|Maor|2007| p=39}} </ref><ref name=Hawking> | |||
| ] | |||
| {{cite book |title=God created the integers: the mathematical breakthroughs that changed history |author=Stephen W. Hawking |page=12 |url=http://books.google.com/?id=3zdFSOS3f4AC&pg=PA12 |isbn=0762419229 |year=2005 |publisher=Running Press Book Publishers |location=Philadelphia}} | |||
| ] gave a proof by dissection in which the pieces do not need to be moved.<ref>{{Cite book |last=Schroeder |first=Manfred Robert |title=Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise |publisher= Courier Corporation |year=2012|pages=3–4|isbn=978-0486134789}}</ref> Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two ] shapes that each include one of two legs instead of the hypotenuse (see ]). In Einstein's proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well. | |||
| </ref> | |||
| ===Euclid's proof=== | ===Euclid's proof=== | ||
| ] | ] | ||
| In outline, here is how the proof in ] '']'' proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details |
In outline, here is how the proof in ]'s '']'' proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be ], proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details follow. | ||
| Let |
Let {{mvar|A}}, {{mvar|B}}, {{mvar|C}} be the ] of a right triangle, with a right angle at {{mvar|A}}. Drop a perpendicular from {{mvar|A}} to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs. | ||
| For the formal proof, we require four elementary ]: | For the formal proof, we require four elementary ]: | ||
| Line 95: | Line 103: | ||
| # The area of a square is equal to the product of two of its sides (follows from 3). | # The area of a square is equal to the product of two of its sides (follows from 3). | ||
| Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.<ref>See for example |
Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.<ref>See for example {{Webarchive|url=https://web.archive.org/web/20161014165156/http://www.slu.edu/classes/maymk/GeoGebra/Pythagoras.html |date=2016-10-14 }}, Saint Louis University website Java applet</ref> | ||
| {{ |
{{Clear}} | ||
| ] | ] | ||
| ] | |||
| The proof is as follows: | The proof is as follows: | ||
| #Let ACB be a right-angled triangle with right angle CAB. | #Let ACB be a right-angled triangle with right angle CAB. | ||
| #On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.<ref name=Gullberg> | #On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.<ref name=Gullberg> | ||
| {{cite book |title=Mathematics: from the birth of numbers |author=Jan Gullberg |page=435 |url= |
{{cite book |title=Mathematics: from the birth of numbers |author=Jan Gullberg |page= |url=https://archive.org/details/mathematicsfromb1997gull |url-access=registration |isbn=0-393-04002-X |year=1997 |publisher=W. W. Norton & Company}} | ||
| </ref> | </ref> | ||
| #From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively. | #From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively. | ||
| #Join CF and AD, to form the triangles BCF and BDA. | #Join CF and AD, to form the triangles BCF and BDA. | ||
| #Angles CAB and BAG are both right angles; therefore C, A, and G are ] |
#Angles CAB and BAG are both right angles; therefore C, A, and G are ]. | ||
| ] | |||
| #Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC. | #Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC. | ||
| #Since AB |
#Since AB is equal to FB, BD is equal to BC and angle ABD equals angle FBC, triangle ABD must be congruent to triangle FBC. | ||
| #Since A is |
#Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2) | ||
| #Since C is collinear with A and G, square BAGF must be twice in area to triangle FBC. | #Since C is collinear with A and G, and this line is parallel to FB, then square BAGF must be twice in area to triangle FBC. | ||
| #Therefore rectangle BDLK must have the same area as square BAGF = AB<sup>2</sup>. | #Therefore, rectangle BDLK must have the same area as square BAGF = AB<sup>2</sup>. | ||
| # |
#By applying steps 3 to 10 to the other side of the figure, it can be similarly shown that rectangle CKLE must have the same area as square ACIH = AC<sup>2</sup>. | ||
| #Adding these two results, AB<sup>2</sup> + AC<sup>2</sup> = BD |
#Adding these two results, AB<sup>2</sup> + AC<sup>2</sup> = BD × BK + KL × KC | ||
| #Since BD = KL, BD |
#Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC | ||
| #Therefore AB<sup>2</sup> + AC<sup>2</sup> = BC<sup>2</sup>, since CBDE is a square. | #Therefore, AB<sup>2</sup> + AC<sup>2</sup> = BC<sup>2</sup>, since CBDE is a square. | ||
| This proof, which appears in Euclid's ''Elements'' as that of Proposition 47 in Book 1,<ref> |
This proof, which appears in Euclid's ''Elements'' as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares.<ref>{{cite web |last=Heiberg |first=J.L. |title= Euclid's Elements of Geometry |url=https://farside.ph.utexas.edu/Books/Euclid/Elements.pdf |pages=46–47}}</ref><ref>{{cite web |title=Euclid's Elements, Book I, Proposition 47 |url=http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI47.html}} See also a by ], Clark University.</ref> | ||
| This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.<ref name=Hawking> | |||
| {{cite book |title=God created the integers: the mathematical breakthroughs that changed history |author=Stephen W. Hawking |page=12 |url=https://books.google.com/books?id=3zdFSOS3f4AC&pg=PA12 |isbn=0-7624-1922-9 |year=2005 |publisher=Running Press Book Publishers |location=Philadelphia}} | |||
| This proof first appeared after a computer program was set to check Euclidean proofs.</ref><ref name=Pythagoras>The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see {{Harv |Maor|2007 |p= }}</ref> | |||
| : web page version using Java applets from by Prof. David E. Joyce, Clark University | |||
| ===Proofs by dissection and rearrangement=== | |||
| </ref> It is therefore an ''areal'' proof in the sense of Dantzig, one that depends on areas, not lengths. This makes it quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.<ref name=Hawking/><ref name=Pythagoras>The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see {{Harv |Maor|2007 |p=25}} </ref> | |||
| Another by rearrangement is given by the middle animation. A large square is formed with area {{math|''c''<sup>2</sup>}}, from four identical right triangles with sides {{mvar|a}}, {{mvar|b}} and {{mvar|c}}, fitted around a small central square. Then two rectangles are formed with sides {{mvar|a}} and {{mvar|b}} by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas {{math|''a''<sup>2</sup>}} and {{math|''b''<sup>2</sup>}}, which must have the same area as the initial large square.<ref>{{cite web |url=http://www.cut-the-knot.org/pythagoras/index.shtml#10 |title= Pythagorean theorem, proof number 10|author=Alexander Bogomolny|author-link=Alexander Bogomolny|work=Cut the Knot |access-date=27 February 2010}}</ref> | |||
| The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called ]. This shows the area of the large square equals that of the two smaller ones.<ref name="specifics">{{Harv|Loomis|1940|loc= Geometric proof 22 and Figure 123| page= 113}}</ref> | |||
| ===A second similarity proof=== | |||
| ] | |||
| {| | |||
| ] can be used in another way to prove the Pythagorean theorem. Corresponding sides of similar polygons are in proportion, and corresponding angles of similar polygons have the same measure. A theorem states that if the homologous or ] of similar polygons are in the ratio ''s'', their areas are in the ratio ''s''<sup>2</sup>.<ref name=Bradbury> | |||
| | ] | |||
| | ] | |||
| | ] | |||
| |} | |||
| ===Proof by area-preserving shearing=== | |||
| ] | |||
| As shown in the accompanying animation, area-preserving ] and translations can transform the squares on the sides adjacent to the right-angle onto the square on the hypotenuse, together covering it exactly.<ref>{{cite book |last1=Polster |first1=Burkard |title=Q.E.D.: Beauty in Mathematical Proof |date=2004 |publisher=Walker Publishing Company |page=49}}</ref> Each shear leaves the base and height unchanged, thus leaving the area unchanged too. The translations also leave the area unchanged, as they do not alter the shapes at all. Each square is first sheared into a parallelogram, and then into a rectangle which can be translated onto one section of the square on the hypotenuse. | |||
| {{cite book |title=An elementary geometry |url=http://books.google.com/books?id=IiYAAAAAYAAJ&pg=PA41 |page=41 |chapter=Theorem XV: Similar polygons are to each other as the squares of the homologous sides |author=William Frothingham Bradbury |year=1872 |publisher=Thompson & Co.}} | |||
| ===Other algebraic proofs=== | |||
| </ref> In particular, this theorem applies to areas of similar right triangles that can be obtained from each other by uniformly "stretching" by the same factor ''s'' in all directions. | |||
| A related proof was published by future U.S. President ] (then a ]).<ref name=Garfield> | |||
| Published in a weekly mathematics column: {{cite journal |journal=The New England Journal of Education |title=Pons Asinorum |volume=3 |issue=14 |page=161 |year=1876 |author=James A Garfield |url=http://www.maa.org/press/periodicals/convergence/mathematical-treasure-james-a-garfields-proof-of-the-pythagorean-theorem }} as noted in {{cite book |title=The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities |url=https://books.google.com/books?id=3tG_FRQ9N1QC&q=New+England+Journal |author=William Dunham |year=1997 |publisher=Wiley |isbn=0-471-17661-3 |page=96 }} and in {{Webarchive|url=https://web.archive.org/web/20100714153516/http://www.math.usma.edu/people/Rickey/hm/Dates/April.pdf |date=July 14, 2010 }} by V. Frederick Rickey | |||
| </ref><ref name=animation>{{cite web|title=Garfield's proof of the Pythagorean Theorem|first=David|last=Lantz|url=http://math.colgate.edu/faculty/dlantz/Pythpfs/Garfldpf.html|website=Math.Colgate.edu|access-date=2018-01-14|archive-url=https://web.archive.org/web/20130828104818/http://math.colgate.edu/faculty/dlantz/Pythpfs/Garfldpf.html|archive-date=2013-08-28|url-status=dead}}</ref><ref>Maor, Eli, ''The Pythagorean Theorem'', Princeton University Press, 2007: pp. 106-107.</ref> Instead of a square it uses a ], which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The ] can be calculated to be half the area of the square, that is | |||
| :<math>\frac{1}{2}(b+a)^2.</math> | |||
| Three triangles can be seen in the first diagram in Euclid's proof above. (They are shown to be similar ].) The large right triangle, with hypotenuse ''c'', is made of the two smaller, similar triangles with hypotenuses ''a'' and ''b''. Thus the area of the large triangle is the sum of areas of the two smaller ones. Let ''f''(α) be the area of a right triangle that has a hypotenuse of unit length and that is similar to these triangles (α selects one of the two corresponding acute angles found in all these triangles). Then the large triangle has an area of ''c''<sup>2</sup>''f''(α), and the smaller two triangles have areas of ''a''<sup>2</sup>''f''(α) and ''b''<sup>2</sup>''f''(α), respectively. Thus ''c''<sup>2</sup>''f''(α) = ''a''<sup>2</sup>''f''(α) + ''b''<sup>2</sup>''f''(α). Dividing by ''f''(α) gives ''c''<sup>2</sup> = ''a''<sup>2</sup> + ''b''<sup>2</sup>. | |||
| The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of <math>\frac{1}{2}</math>, which is removed by multiplying by two to give the result. | |||
| A modification of this proof avoids a direct use of the result that the area is multiplied by ''s''<sup>2</sup> when an object is scaled by a factor of ''s''. The modified proof notes that each square shares a side with the hypotenuse of a triangle, so similarity between selected squares and similarity of the related triangles forces their area ratios to be the same. (These area ratios are, of course, the ratios of the squares of the hypotenuses, but those details need not be used explicitly.) Because the area of the large triangle is the sum of the areas of the smaller two, the area of the large square must be the sum of the areas of the smaller two squares as well. | |||
| This approach can be compared with the ]. | |||
| ===Proof by rearrangement=== | |||
| ] | |||
| ] | |||
| ] | |||
| In the animation at the left, the total area and the areas of the triangles are all constant. Therefore, the total black area is constant. But the original black area of side ''c'' can be divided into two squares delineated by the triangle sides ''a'', ''b'', demonstrating {{nowrap|that ''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>.}} | |||
| Another proof by rearrangement is given by the animation at the right. An initial large square is formed of area ''c''<sup>2</sup> by adjoining four identical right triangles, leaving a small square in the center of the big square to accommodate the difference in lengths of the sides of the triangles. Two rectangles are formed of sides ''a'' and ''b'' by moving the triangles. By incorporating the center small square with one of these rectangles, the two rectangles are made into two squares of areas ''a''<sup>2</sup> and ''b''<sup>2</sup>, showing {{nowrap|that ''c''<sup>2</sup> {{=}} ''a''<sup>2</sup> + ''b''<sup>2</sup>.}} | |||
| <!--Images put in a row in order to avoid blank lines--> | |||
| A third graphic illustration of the Pythagorean theorem (in shades of green and blue to the right) fits parts of the sides' squares into the hypotenuse's square. This example is one of many complex geometric proofs described by Loomis.<ref name=specifics>{{Harv|Loomis|1968|loc= Geometric proof 22 and Figure 123, page= 113}}</ref> The corresponding blue– and green–shaded areas are equal. Because the sum of equals are equal, the large bottom square composed of its blue and green pieces has the same area as the sum of the upper two squares made up of the same pieces. A complete proof would describe how the various parts are generated, and show that the repositioned parts fit into and fill the lower square. A ] ] on line shows how to cut the small square in more and more slices as the corresponding side gets smaller and smaller.<ref> by Alexander Bogomolny. Retrieved 19 December 2006.</ref> | |||
| ===Algebraic proof=== | |||
| ] | |||
| An algebraic proof is provided by the following reasoning. A point is marked on each side of the outer square, dividing each side into two segments of lengths ''a'' and ''b''. As shown in the illustration, the result is a large square with identical right triangles in its corners. Each pair of triangles from opposite corners forms a rectangle with area ''ab'', so the area of all four triangles is: | |||
| *''Area of'' 4 ''triangles'' = 2''ab''. | |||
| The center figure has equal sides because all the four triangles forming its border are the same. However, it might be any kind of ]. Next, the center figure is shown to be a square: The ''a''-side angle and ''b''-side angle of each of these triangles are ], that is, they sum to a right angle. However, the corner angle ''c'' of the inner figure and the two side-angles ''a'' and ''b'' sum to a straight angle. So each of the angles of the blue area in the middle is a right angle, making this area a square with side length ''c''. The area of this square is ''c''<sup>2</sup>. Thus the area of everything together is given by: | |||
| *''Area of complete figure'' = ''c''<sup>2</sup> + 2''ab''. | |||
| However, as the large square has sides of length {{nowrap|''a'' + ''b''}}, we can also calculate its area as: | |||
| *''Area of complete figure'' = {{nowrap|(''a'' + ''b'')<sup>2</sup> {{=}} ''a''<sup>2</sup> + 2''ab'' + ''b''<sup>2</sup>.}} | |||
| Equating the two expressions for the total area, the result is: | |||
| : <math>a^2+b^2+2ab= c^2+2ab .\,\!</math> | |||
| A term of 2''ab'' can be subtracted from both sides of the equation, leaving: | |||
| :<math> a^2+ b^2= c^2.\,\!</math> | |||
| which is Pythagoras' theorem. | |||
| ====Proof by subtraction==== | |||
| ] | |||
| In a rearrangement version of this proof, the figure shows two identical large squares of side {{nowrap|''a'' + ''b''}}. The left square contains the square on the hypotenuse plus identical right triangles in its four corners. On the right, the same large square holds the squares on the other two sides plus the same four right triangles, now moved to form two rectangles of sides ''a'' and ''b'' in the bottom corners. From both identical large squares, the area of the same four right triangles of sides ''a, b, c'' is subtracted (colored). Subtracting the triangles removes the same (colored) area from the equal-area large squares, so the remaining white areas, ''c''<sup>2</sup> and {{nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup>}}, are equal. | |||
| ====Proof by areas==== | |||
| ] | |||
| A related algebraic proof uses four rotations of a triangle of sides ''a'', ''b'', and ''c''.<ref name=rotate> | |||
| {{cite web |url=http://www.cut-the-knot.org/pythagoras/index.shtml#3 |title=Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3 |author=Alexander Bogomolny |date= |work=Cut the Knot |publisher= |accessdate=16 June 2010}} | |||
| </ref> By the fourfold symmetry of the square, all four right triangles are identical. The area of the top figure is the sum of the areas of four triangles (2''ab'') and the center square has side length {{nowrap|''b'' − ''a''}} and therefore area {{nowrap|(''b'' − ''a'')<sup>2</sup>}}, so: | |||
| :<math>A = (b-a)^2+2ab = a^2+b^2. \, </math> | |||
| The area of a square of side ''c'' is ''A'' = ''c''<sup>2</sup>. Hence, | |||
| :<math>c^2 = a^2 + b^2. \, </math> | |||
| ===Proof using differentials=== | ===Proof using differentials=== | ||
| One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing ].<ref name="Staring"> | |||
| {{cite journal |doi=10.2307/2691395 |title=The Pythagorean proposition: A proof by means of calculus |author=Mike Staring |journal=Mathematics Magazine |publisher=Mathematical Association of America |volume=69 |number=1 |pages=45–46 |year=1996 |jstor=2691395 }} | |||
| </ref><ref name=M_Hardy> | |||
| {{cite web |url=http://www.cut-the-knot.org/pythagoras |title=Pythagorean Theorem |access-date=2010-05-09 |last=Bogomolny |first=Alexander |work=Interactive Mathematics Miscellany and Puzzles |publisher=Alexander Bogomolny |url-status=dead |archive-url=https://web.archive.org/web/20100706200930/http://www.cut-the-knot.org/pythagoras/ |archive-date=2010-07-06 }} | |||
| </ref><ref> | |||
| {{cite journal |author= Bruce C. Berndt |title= Ramanujan – 100 years old (fashioned) or 100 years new (fangled)? |journal= The Mathematical Intelligencer |volume= 10 |pages= 24–31 |year= 1988 |doi=10.1007/BF03026638 |issue= 3|s2cid= 123311054 }} | |||
| </ref> | |||
| The triangle ''ABC'' is a right triangle, as shown in the upper part of the diagram, with ''BC'' the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length {{mvar|y}}, the side ''AC'' of length {{mvar|x}} and the side ''AB'' of length {{mvar|a}}, as seen in the lower diagram part. | |||
| One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing a little ].<ref name="Staring"> | |||
| {{cite journal |doi=10.2307/2691395 |title=The Pythagorean proposition: A proof by means of calculus |author=Mike Staring |journal=Mathematics Magazine |publisher=Mathematical Association of America |volume=69 |number=1 |pages=45–46 |year=1996 |issue=February |url=http://www.jstor.org/stable/2691395 |ref=harv}} <br> | |||
| (An abbreviated version of this proof is in the second half of at {{cite web|url=http://www.cut-the-knot.org/pythagoras |title=Pythagorean Theorem |accessdate=2010-05-09 |last=Bogomolny |first=Alexander |work= |publisher=Alexander Bogomolny }} ) | |||
| </ref><ref name=M_Hardy> also summarizes a differential proof by Michael Hardy: "Pythagoras Made Difficult". '']'', '''10''' (3), p. 31, 1988. Although not listed in this journal's table of contents and without a doi, this article can be found at the end of the unrelated article by {{cite journal |author= Bruce C. Berndt |title= Ramanujan—100 years old (fashioned) or 100 years new (fangled)? |journal= The Mathematical Intelligencer |volume= 10 |pages= 24 |year= 1988 |doi=10.1007/BF03026638 |ref= harv}}</ref> This proof is a ''metric'' proof in the sense of Dantzig, as it uses lengths, not areas. | |||
| ] | |||
| In the figure, triangle PBC is the original right triangle and triangle ABC is the modification of PBC when side PB is extended by increasing ''a'' to ''a'' + Δ''a''. The circular arcs have radii ''c'' and ''c'' + Δ''c'' where Δ''c'' is the change in hypotenuse ''c'' that occurs as a result of the change Δ''a'' in side ''a''. | |||
| If {{mvar|x}} is increased by a small amount ''dx'' by extending the side ''AC'' slightly to {{mvar|D}}, then {{mvar|y}} also increases by ''dy''. These form two sides of a triangle, ''CDE'', which (with {{mvar|E}} chosen so ''CE'' is perpendicular to the hypotenuse) is a right triangle approximately similar to ''ABC''. Therefore, the ratios of their sides must be the same, that is: | |||
| :<math> \frac{dy}{dx}=\frac xy.</math> | |||
| ] | |||
| This can be rewritten as <math>y \, dy=x \, dx</math> , which is a ] that can be solved by direct integration: | |||
| :<math>\int y \, dy=\int x \, dx\,,</math> | |||
| The figure shows two constructions, right triangles ADP and AQP, in the upper and lower panels which will be used to find respectively ] of the ] {{nowrap|Δ''c''/Δ''a''.}} Then the limit will be taken as {{nowrap|Δ''a'', Δ''c'' → 0,}} and the resulting expression for the ] {{nowrap|''dc'' /''da''}} will be used to establish Pythagoras' theorem. | |||
| giving | |||
| :<math>y^2=x^2+C.</math> | |||
| From triangle ABC (upper panel), | |||
| The constant can be deduced from {{math|1=''x'' = 0}}, {{math|1=''y'' = ''a''}} to give the equation | |||
| :<math>\cos \theta = \frac{AB}{AC} = \frac{a + \Delta a}{c+\Delta c}.</math> | |||
| :<math>y^2 = x^2 + a^2.</math> | |||
| This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of ''dx'' and ''dy''. | |||
| Construct right triangle ADP (upper panel). Then, | |||
| :<math>\cos \theta = \frac{AD}{AP} = \frac{AD}{\Delta a} > \frac{\Delta c}{\Delta a}.</math> | |||
| The last inequality results from ''AD'' > Δ''c'' , as shown in the upper panel of the figure.<ref name="aside"> | |||
| From the figure, it is evident that point D lies inside the circle of radius ''c'', which is why ''AD'' is larger than Δ''c''. That fact is rigorously established by noting side ''CD'' of right triangle CDP must be less than ''c'' because it is necessarily less than the hypotenuse ''CP'' of CDP. Consequently, point D definitely is inside the circle of radius ''c''. Similarly, point Q must lie inside the circle of radius ''c'' + Δ''c'' because ''CQ'' must be less than the hypotenuse ''CA'' of right triangle CQA, of length ''c'' + Δ''c''. The theorem that the hypotenuse of a right triangle is longer than either of its sides ], so the derivation is not simply circular. However, that theorem in turn does require the ], equivalent to Euclid's ]. | |||
| </ref> Combining the above expressions for cos ''θ'', | |||
| :<math>\frac{\Delta c}{\Delta a} < \frac{a + \Delta a}{c+\Delta c}.</math> | |||
| Next construct right triangle AQP (lower panel). Since both triangles AQP and PBC have an angle <math> \scriptstyle \phi </math>, | |||
| :<math> \cos \phi = \frac{a}{c} =\frac{PQ}{PA}= \frac{PQ}{\Delta a} < \frac{\Delta c}{\Delta a}.</math> | |||
| The last inequality results from {{nowrap|''PQ'' < Δ''c'',}} as shown in the lower panel of the figure. Combining the two inequalities that were obtained using triangles ADP and AQP, | |||
| :<math>\frac{a}{c} < \frac{\Delta c}{\Delta a} < \frac{a + \Delta a}{c+\Delta c} = \left(\frac{a}{c} \right) \frac{1+ \Delta a /a}{1+\Delta c /c}.</math> | |||
| We now have upper and lower bounds for the ratio {{nowrap|Δ''c'' /Δ''a''}}. {{nowrap|As Δ''a'', Δ''c'' → 0,}} the ratio {{nowrap|Δ''c'' /Δ''a''}} becomes the derivative {{nowrap|''dc'' /''da''}} and the upper bound becomes the same as the lower bound {{nowrap|''a'' /''c''.}} Consequently, | |||
| :<math>\frac {dc}{da} =\frac{a}{c}, </math> | |||
| or: | |||
| :<math>c \, dc = a \, da; \ d (c^2) = d (a^2), </math> | |||
| which has the ]: | |||
| :<math> c^2 = a^2 + \text{ constant}.\,</math> | |||
| When ''a'' = 0 then ''c'' = ''b'', so the "constant" is {{nowrap|''b''<sup>2</sup>.}} Hence, Pythagoras' theorem is established: | |||
| :<math>c^2 = a^2 + b^2.\,</math> | |||
| Using this expression, the ] is: | |||
| :<math> d(c^2) = d(a^2) +d(b^2).\,</math> | |||
| This result shows that the increase in the square of the hypotenuse is the sum of the independent contributions from the squares of the sides. | |||
| ===Garfield's proof=== | |||
| ] | |||
| Major general ] (later President of the United States) published a novel algebraic proof based upon equating two different determinations of the area of a trapezoid.<ref name=Garfield>Published in a weekly mathematics column: {{cite journal |journal=The New England Journal of Education |volume=3 |page=161 |year=1876 |author=James A Garfield |ref=harv}} as noted in {{cite book |title=The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities |url=http://books.google.com/?id=3tG_FRQ9N1QC&cd=1&dq=%22mathematical+universe%22+inauthor%3AWilliam+inauthor%3ADunham&q=New+England+Journal#search_anchor |author=William Dunham |year=1997 |publisher=Wiley |isbn=0471176613 |page=96}} and in by V. Frederick Rickey | |||
| </ref><ref name=animation> from his </ref> | |||
| The ] is | |||
| : <math>A=\frac{s_1 + s_2}{2}\ h</math> | |||
| where , <math>s_1=a</math> and <math>s_2 = b</math> are lengths of the parallel sides, and <math>h = a + b</math> is the height. The formula can be viewed as the average width of the trapezoid times the height. | |||
| Substituting for the sides and height, the area of the trapezoid in the figure is | |||
| : <math>A=\frac{(a+b)}{2}(a + b) = \frac{(a+b)^2}{2}</math>. | |||
| Identical right-angle triangles 1 and 2 each have area <math> \frac{ab}{2} </math>, while right-angle triangle 3 has area <math> \frac{c^2}{2} </math>, which happens to be half of the square on the hypotenuse of triangle 1 or triangle 2. | |||
| Therefore, the area of the entire trapezoid is: | |||
| : <math>A = \frac{ab}{2} + \frac{ab}{2} + \frac{c^2}{2} = ab + \frac{c^2}{2}. </math> | |||
| These two area determinations must be equal, so | |||
| :<math>\begin{align} | |||
| ab + \frac{c^2}{2} &= \frac{(a+b)^2}{2},\\ | |||
| &= \frac{a^2 + 2ab + b^2}{2} .\\ | |||
| \end{align}</math> | |||
| Multiplying by 2 and rearranging: | |||
| :<math> c^2 +2ab = a^2 + b^2 + 2ab \ .</math> | |||
| Subtracting <math>2ab</math> from both sides, the square on the hypotenuse of either triangle 1 or triangle 2 is found to be equal to the sum of the squares on the other two sides: | |||
| : <math> c^2= a^2 + b^2 . \, </math> | |||
| ==Converse== | ==Converse== | ||
| The ] of the theorem is also true:<ref name=Sally1> | The ] of the theorem is also true:<ref name=Sally1> | ||
| {{cite book |title= Roots to Research |author1=Judith D. Sally |author2=Paul J. Sally Jr. |pages = 54–55 |chapter=Theorem 2.4 (Converse of the Pythagorean theorem). |chapter-url=https://books.google.com/books?id=nHxBw-WlECUC&pg=PA54 | publisher= ] | |||
| |isbn=978-0-8218-4403-8 |date=2007-12-21 }} | |||
| {{cite book |title=Cited work |author=Judith D. Sally, Paul Sally |page=62 |chapter=Theorem 2.4 (Converse of the Pythagorean Theorem). |url=http://books.google.com/books?id=nHxBw-WlECUC&pg=PA54 | |||
| |isbn=0821844032 |date=2007-12-21 }} | |||
| </ref> | </ref> | ||
| <blockquote>For any three positive numbers ''a'', ''b'', and ''c'' such that {{nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}}, there exists a triangle with sides ''a'', ''b'' and ''c'', and every such triangle has a right angle between the sides of lengths ''a'' and ''b''.</blockquote> | |||
| <blockquote>Given a triangle with sides of length {{mvar|a}}, {{mvar|b}}, and {{mvar|c}}, if {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>,}} then the angle between sides {{mvar|a}} and {{mvar|b}} is a ].</blockquote> | |||
| Such numbers are called a ]. An alternative statement is: | |||
| For any three positive ] {{mvar|a}}, {{mvar|b}}, and {{mvar|c}} such that {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>}}, there exists a triangle with sides {{mvar|a}}, {{mvar|b}} and {{mvar|c}} as a consequence of the ]. | |||
| This converse |
This converse appears in Euclid's ''Elements'' (Book I, Proposition 48): "If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."<ref> | ||
| From at Clark University | From at Clark University | ||
| </ref> | |||
| </ref> {{blockquote|text="If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."}} | |||
| It can be |
It can be proved using the ] or as follows: | ||
| Let ''ABC'' be a triangle with side lengths |
Let ''ABC'' be a triangle with side lengths {{mvar|a}}, {{mvar|b}}, and {{mvar|c}}, with {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>.}} Construct a second triangle with sides of length {{mvar|a}} and {{mvar|b}} containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length {{math|1=''c'' = {{radic|''a''<sup>2</sup> + ''b''<sup>2</sup>}}}}, the same as the hypotenuse of the first triangle. Since both triangles' sides are the same lengths {{mvar|a}}, {{mvar|b}} and {{mvar|c}}, the triangles are ] and must have the same angles. Therefore, the angle between the side of lengths {{mvar|a}} and {{mvar|b}} in the original triangle is a right angle. | ||
| The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proved without assuming the Pythagorean theorem.<ref>Casey, Stephen, "The converse of the theorem of Pythagoras", '']'' 92, July 2008, 309–313.</ref><ref>Mitchell, Douglas W., "Feedback on 92.47", ''Mathematical Gazette'' 93, March 2009, 156.</ref> | |||
| A ] of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Where ''c'' is chosen to be the longest of the three sides and {{nowrap|''a'' + ''b'' > ''c''}} (otherwise there is ''no'' triangle according to the ]). The following statements apply:<ref name=Wilczynski> | |||
| {{cite book |title=Plane trigonometry and applications |author=Ernest Julius Wilczynski, Herbert Ellsworth Slaught |page=85 |url=http://books.google.com/?id=vxk3AAAAMAAJ&pg=PA85 |chapter=Theorem 1 and Theorem 2 |year=1914 |publisher=Allyn and Bacon}} | |||
| A ] of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let {{mvar|c}} be chosen to be the longest of the three sides and {{math|''a'' + ''b'' > ''c''}} (otherwise there is no triangle according to the ]). The following statements apply:<ref name=Wilczynski> | |||
| {{cite book |title=Plane trigonometry and applications |author1=Ernest Julius Wilczynski |author2=Herbert Ellsworth Slaught |author2-link=Herbert Ellsworth Slaught|page= |url=https://archive.org/details/planetrigonomet00wilcgoog |chapter=Theorem 1 and Theorem 2 |year=1914 |publisher=Allyn and Bacon}} | |||
| </ref> | </ref> | ||
| * If {{ |
* If {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>,}} then the ]. | ||
| * If {{ |
* If {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> > ''c''<sup>2</sup>,}} then the ]. | ||
| * If {{ |
* If {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> < ''c''<sup>2</sup>,}} then the ]. | ||
| ] has stated this proposition about acute, right, and obtuse triangles in this language: | ] has stated this proposition about acute, right, and obtuse triangles in this language: | ||
| :{{ |
:{{math|sgn(''α'' + ''β'' − ''γ'') {{=}} sgn(''a''<sup>2</sup> + ''b''<sup>2</sup> − ''c''<sup>2</sup>),}} | ||
| where |
where {{mvar|α}} is the angle opposite to side {{mvar|a}}, {{mvar|β}} is the angle opposite to side {{mvar|b}}, {{mvar|γ}} is the angle opposite to side {{mvar|c}}, and sgn is the ].<ref>{{cite web|url=http://www.cs.utexas.edu/users/EWD/transcriptions/EWD09xx/EWD975.html|title=On the theorem of Pythagoras|first= Edsger W.|last=Dijkstra|author-link=Edsger W. Dijkstra|date=September 7, 1986|work=EWD975|publisher=E. W. Dijkstra Archive}}</ref> | ||
| ==Consequences and uses of the theorem== | ==Consequences and uses of the theorem== | ||
| ===Pythagorean triples=== | ===Pythagorean triples=== | ||
| {{Main|Pythagorean triple}} | {{Main|Pythagorean triple}} | ||
| {{See also|Formulas for generating Pythagorean triples}} | |||
| A Pythagorean triple has three positive integers ''a'', ''b'', and ''c'', such that {{nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>.}} In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.<ref name=Sally0/> Evidence from megalithic monuments on the Northern Europe shows that such triples were known before the discovery of writing. Such a triple is commonly written {{nowrap|(''a'', ''b'', ''c'').}} Some well-known examples are {{nowrap|(3, 4, 5)}} and {{nowrap|(5, 12, 13).}} | |||
| A Pythagorean triple has three positive integers {{mvar|a}}, {{mvar|b}}, and {{mvar|c}}, such that {{math|''a''<sup>2</sup> + ''b''<sup>2</sup> {{=}} ''c''<sup>2</sup>.}} In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths.<ref name=Sally0/> Such a triple is commonly written {{math|(''a'', ''b'', ''c'').}} Some well-known examples are {{math|(3, 4, 5)}} and {{math|(5, 12, 13).}} | |||
| A primitive Pythagorean triple is one in which |
A primitive Pythagorean triple is one in which {{mvar|a}}, {{mvar|b}} and {{mvar|c}} are ] (the ] of {{mvar|a}}, {{mvar|b}} and {{mvar|c}} is 1). | ||
| The following is a list of primitive Pythagorean triples with values less than 100: | The following is a list of primitive Pythagorean triples with values less than 100: | ||
| Line 313: | Line 229: | ||
| :(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97) | :(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97) | ||
| There are many ]. Of these, '''Euclid's formula''' is the most well-known: given arbitrary positive integers {{mvar|m}} and {{mvar|n}}, the formula states that the integers | |||
| ===Incommensurable lengths=== | |||
| :<math> a = m^2 - n^2 ,\quad \, b = 2mn ,\quad \, c = m^2 + n^2</math> | |||
| ] | |||
| forms a Pythagorean triple. | |||
| One of the consequences of the Pythagorean theorem is that line segments whose lengths are ] (that is, whose ratio is an ]) can be constructed using a ]. Pythagoras' theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides ''via'' the ] operation. | |||
| ===Inverse Pythagorean theorem=== | |||
| The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.<ref name=Euclid_5> | |||
| Given a ] with sides <math>a,b,c</math> and ] <math>d</math> (a line from the right angle and perpendicular to the ] <math>c</math>). The Pythagorean theorem has, | |||
| :<math>a^2+b^2 = c^2</math> | |||
| while the ] relates the two ] <math>a,b</math> to the altitude <math>d</math>,<ref>Alexander Bogomolny, Pythagorean Theorem for the Reciprocals,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml</ref> | |||
| :<math>\frac1{a^2}+\frac1{b^2} = \frac1{d^2}</math> | |||
| The equation can be transformed to, | |||
| :<math>\frac1{(xz)^2}+\frac1{(yz)^2} = \frac1{(xy)^2}</math> | |||
| where <math>x^2+y^2=z^2</math> for any non-zero ] <math>x,y,z</math>. If the <math>a,b,d</math> are to be ]s, the smallest solution <math>a>b>d</math> is then | |||
| :<math>\frac1{20^2}+\frac1{15^2} = \frac1{12^2}</math> | |||
| using the smallest Pythagorean triple <math>3,4,5</math>. The reciprocal Pythagorean theorem is a special case of the ] | |||
| :<math>\frac1{p}+\frac1{q} = \frac1{r}</math> | |||
| where the denominators are squares and also for a ] whose sides <math>p,q,r</math> are square numbers. | |||
| ===Incommensurable lengths=== | |||
| {{cite book |title=The elements of Euclid: with many additional propositions, & explanatory notes to which is prefixed an introductory essay on logic|author=Henry Law |publisher=John Weale |year=1853 |url=http://books.google.com/?id=Ssb_OnVOGLgC&pg=PA49 |page=49 |chapter=Corollary 5 of Proposition XLVII, ''Pythagoras' Theorem''}} | |||
| ]: A construction for line segments with lengths whose ratios are the square root of a positive integer]] | |||
| One of the consequences of the Pythagorean theorem is that line segments whose lengths are ] (so the ratio of which is not a ]) can be constructed using a ]. Pythagoras' theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the ] operation. | |||
| </ref> Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras' theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit |
The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer.<ref name=Euclid_5>{{cite book |title=The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic |first=Henry |last=Law |publisher=John Weale |year=1853 |chapter-url=https://books.google.com/books?id=Ssb_OnVOGLgC&pg=PA49 |page=49 |chapter=Corollary 5 of Proposition XLVII (''Pythagoras's Theorem'')}}</ref> Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras' theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as {{radical|2}}, {{radical|3}}, {{radical|5}} . For more detail, see ]. | ||
| Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.<ref name=Lavine0> | Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit.<ref name=Lavine0> | ||
| {{cite book |title=Understanding the infinite |author=Shaughan Lavine |page=13 |url= |
{{cite book |title=Understanding the infinite |author=Shaughan Lavine |page=13 |url=https://books.google.com/books?id=GvGqRYifGpMC&pg=PA13 |isbn=0-674-92096-1 |year=1994 |publisher=Harvard University Press}} | ||
| </ref> |
</ref> According to one legend, ] (''ca.'' 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable.<ref name=drown> | ||
| {{Harv|Heath|1921|loc= Vol I, pp. 65}}; Hippasus |
{{Harv|Heath|1921|loc= Vol I, pp. 65}}; Hippasus was on a voyage at the time, and his fellows cast him overboard. See {{cite journal |author= James R. Choike |title= The pentagram and the discovery of an irrational number |journal=The College Mathematics Journal |volume=11 |pages=312–316 |year=1980 }} | ||
| </ref |
</ref> | ||
| A careful discussion of Hippasus' contributions is found in | A careful discussion of Hippasus's contributions is found in ].<ref name=Fritz> | ||
| {{cite journal |title=The Discovery of Incommensurability by Hippasus of Metapontum |
{{cite journal |title=The Discovery of Incommensurability by Hippasus of Metapontum |author=Kurt Von Fritz |journal=Annals of Mathematics | series = Second Series|volume= 46 |date=Apr 1945|pages= 242–264 |jstor=1969021 |issue= 2 |doi=10.2307/1969021}} | ||
| </ref> | </ref> | ||
| ===Complex numbers=== | |||
| ===Euclidean distance in various coordinate systems=== | |||
| ] | |||
| ] is given by the ]. Interior angle Δθ = θ<sub>1</sub>−θ<sub>2</sub>.]] | |||
| For any ] | |||
| The distance formula in ] is derived from the Pythagorean theorem.<ref name=Macdonald> | |||
| :<math>z = x + iy,</math> | |||
| the ] or modulus is given by | |||
| :<math>r = |z|=\sqrt{x^2 + y^2}.</math> | |||
| So the three quantities, {{mvar|r}}, {{mvar|x}} and {{mvar|y}} are related by the Pythagorean equation, | |||
| :<math>r^2 = x^2 + y^2.</math> | |||
| Note that {{mvar|r}} is defined to be a positive number or zero but {{mvar|x}} and {{mvar|y}} can be negative as well as positive. Geometrically {{mvar|r}} is the distance of the {{mvar|z}} from zero or the origin {{mvar|O}} in the ]. | |||
| This can be generalised to find the distance between two points, {{math|''z''<sub>1</sub>}} and {{math|''z''<sub>2</sub>}} say. The required distance is given by | |||
| {{cite book |title=Mastering algorithms with Perl |author=Jon Orwant, Jarkko Hietaniemi, John Macdonald |url=http://books.google.com/books?id=z9xMfXGoWd0C&pg=PA426 |page=426 |chapter=Euclidean distance |isbn=1565923987 |year=1999 |publisher=O'Reilly Media, Inc}} | |||
| :<math>|z_1 - z_2|=\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2},</math> | |||
| so again they are related by a version of the Pythagorean equation, | |||
| :<math>|z_1 - z_2|^2 = (x_1 - x_2)^2 + (y_1 - y_2)^2.</math> | |||
| ===Euclidean distance=== | |||
| </ref> If {{nowrap|(''x''<sub>1</sub>, ''y''<sub>1</sub>)}} and {{nowrap|(''x''<sub>2</sub>, ''y''<sub>2</sub>)}} are points in the plane, then the distance between them, also called the ], is given by | |||
| {{main|Euclidean distance}} | |||
| The distance formula in ] is derived from the Pythagorean theorem.<ref name=Macdonald>{{cite book |title=Mastering algorithms with Perl |author1=Jon Orwant |author2=Jarkko Hietaniemi |author3=John Macdonald |chapter-url=https://books.google.com/books?id=z9xMfXGoWd0C&pg=PA426 |page=426 |chapter=Euclidean distance |isbn=1-56592-398-7 |year=1999 |publisher=O'Reilly Media, Inc.}}</ref> If {{math|(''x''<sub>1</sub>, ''y''<sub>1</sub>)}} and {{math|(''x''<sub>2</sub>, ''y''<sub>2</sub>)}} are points in the plane, then the distance between them, also called the ], is given by | |||
| :<math> \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}. </math> | :<math> \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}. </math> | ||
| More generally, in ], the Euclidean distance between two points, <math>A\,=\,(a_1,a_2,\dots,a_n)</math> and <math>B\,=\,(b_1,b_2,\dots,b_n)</math>, is defined, by generalization of the Pythagorean theorem, as: | More generally, in ], the Euclidean distance between two points, <math>A\,=\,(a_1,a_2,\dots,a_n)</math> and <math>B\,=\,(b_1,b_2,\dots,b_n)</math>, is defined, by generalization of the Pythagorean theorem, as: | ||
| :<math>\sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2} = \sqrt{\sum_{i=1}^n (a_i-b_i)^2}.</math> | :<math>\sqrt{(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2} = \sqrt{\sum_{i=1}^n (a_i-b_i)^2}.</math> | ||
| If instead of Euclidean distance, the square of this value (the ], or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates: | |||
| If Cartesian coordinates are ''not'' used, for example, if ] are used in two dimensions or, in more general terms, if ] are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the ]. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates {{nowrap|(''r'', ''θ'')}} can be introduced as: | |||
| :<math>(a_1-b_1)^2 + (a_2-b_2)^2 + \cdots + (a_n-b_n)^2 = \sum_{i=1}^n (a_i-b_i)^2.</math> | |||
| The squared form is a smooth, ] of both points, and is widely used in ] and ], forming the basis of ]. | |||
| ===Euclidean distance in other coordinate systems=== | |||
| If Cartesian coordinates are not used, for example, if ] are used in two dimensions or, in more general terms, if ] are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the ]. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates {{math|(''r'', ''θ'')}} can be introduced as: | |||
| :<math> x = r \cos \theta, \ y = r \sin \theta. |
:<math> x = r \cos \theta, \ y = r \sin \theta.</math> | ||
| Then two points with locations {{ |
Then two points with locations {{math|(''r''<sub>1</sub>, ''θ''<sub>1</sub>)}} and {{math|(''r''<sub>2</sub>, ''θ''<sub>2</sub>)}} are separated by a distance {{mvar|s}}: | ||
| :<math>s^2 = (x_1 - x_2)^2 + (y_1-y_2)^2 = (r_1 \cos \theta_1 -r_2 \cos \theta_2 )^2 + (r_1 \sin \theta_1 -r_2 \sin \theta_2)^2. |
:<math>s^2 = (x_1 - x_2)^2 + (y_1-y_2)^2 = (r_1 \cos \theta_1 -r_2 \cos \theta_2 )^2 + (r_1 \sin \theta_1 -r_2 \sin \theta_2)^2.</math> | ||
| Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as: | Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as: | ||
| :<math>\begin{align}s^2 &= r_1^2 +r_2^2 -2 r_1 r_2 \left( \cos \theta_1 \cos \theta_2 +\sin \theta_1 \sin \theta_2 \right)\\ | :<math>\begin{align}s^2 &= r_1^2 +r_2^2 -2 r_1 r_2 \left( \cos \theta_1 \cos \theta_2 +\sin \theta_1 \sin \theta_2 \right)\\ | ||
| &= r_1^2 +r_2^2 -2 r_1 r_2 \cos \left( \theta_1 - \theta_2\right)\\ | &= r_1^2 +r_2^2 -2 r_1 r_2 \cos \left( \theta_1 - \theta_2\right)\\ | ||
| &=r_1^2 +r_2^2 -2 r_1 r_2 \cos \Delta \theta \end{align} |
&=r_1^2 +r_2^2 -2 r_1 r_2 \cos \Delta \theta, \end{align}</math> | ||
| using the trigonometric ]. This formula is the ], sometimes called the |
using the trigonometric ]. This formula is the ], sometimes called the generalized Pythagorean theorem.<ref>{{Cite book | ||
| |title=Plane Trigonometry and Tables | |title=Plane Trigonometry and Tables | ||
| |first1=George | |first1=George | ||
| Line 368: | Line 316: | ||
| |publisher=BiblioBazaar, LLC | |publisher=BiblioBazaar, LLC | ||
| |year=2009 | |year=2009 | ||
| |isbn=1-103-07998- |
|isbn=978-1-103-07998-8 | ||
| |page=116 | |page=116 | ||
| |url= |
|url=https://books.google.com/books?id=Z-O57gUYmIgC | ||
| }}, | |||
| </ref> From this result, for the case where the radii to the two locations are at right angles, the enclosed angle {{ |
</ref> From this result, for the case where the radii to the two locations are at right angles, the enclosed angle {{math|Δ''θ'' {{=}} {{pi}}/2,}} and the form corresponding to Pythagoras' theorem is regained: <math>s^2 = r_1^2 + r_2^2.</math> The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles. | ||
| ===Pythagorean trigonometric identity=== | ===Pythagorean trigonometric identity=== | ||
| {{Main|Pythagorean trigonometric identity}} | {{Main|Pythagorean trigonometric identity}} | ||
| ] | ] | ||
| In a right triangle with sides ''a'', ''b'' and hypotenuse ''c'', ] determines the ] and ] of the angle ''θ'' between side ''a'' and the hypotenuse as: | |||
| In a right triangle with sides {{mvar|a}}, {{mvar|b}} and hypotenuse {{mvar|c}}, ] determines the ] and ] of the angle {{mvar|θ}} between side {{mvar|a}} and the hypotenuse as: | |||
| :<math>\sin \theta = \frac{b}{c}, \quad \cos \theta = \frac{a}{c}.</math> | :<math>\sin \theta = \frac{b}{c}, \quad \cos \theta = \frac{a}{c}.</math> | ||
| Line 384: | Line 333: | ||
| :<math> {\cos}^2 \theta + {\sin}^2 \theta = \frac{a^2 + b^2}{c^2} = 1,</math> | :<math> {\cos}^2 \theta + {\sin}^2 \theta = \frac{a^2 + b^2}{c^2} = 1,</math> | ||
| where the last step applies Pythagoras' theorem. This relation between sine and cosine |
where the last step applies Pythagoras' theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.<ref name= Leff> | ||
| {{cite book |title=PreCalculus the Easy Way |author=Lawrence S. Leff |url= |
{{cite book |title=PreCalculus the Easy Way |author=Lawrence S. Leff |url=https://archive.org/details/precalculuseasyw00lawr |url-access=registration |page= |isbn=0-7641-2892-2 |edition=7th |publisher=Barron's Educational Series |year=2005}} | ||
| </ref> In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin |
</ref> In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size {{math|sin ''θ''}} and adjacent side of size {{math|cos ''θ''}} in units of the hypotenuse. | ||
| ===Relation to the cross product=== | |||
| ] | |||
| The Pythagorean theorem relates the ] and ] in a similar way:<ref name=Massey> | |||
| {{cite journal |doi=10.2307/2323537 |title=Cross products of vectors in higher-dimensional Euclidean spaces |author=WS Massey |journal=The American Mathematical Monthly |volume=90 |date=Dec 1983 |pages=697–701 |jstor=2323537 |issue=10 |publisher=Mathematical Association of America |s2cid=43318100 |url=https://pdfs.semanticscholar.org/1f6b/ff1e992f60eb87b35c3ceed04272fb5cc298.pdf |archive-url=https://web.archive.org/web/20210226011747/https://pdfs.semanticscholar.org/1f6b/ff1e992f60eb87b35c3ceed04272fb5cc298.pdf |url-status=dead |archive-date=2021-02-26 }} | |||
| </ref> | |||
| :<math> \|\mathbf{a} \times \mathbf{b}\|^2 + (\mathbf{a} \cdot \mathbf{b})^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2.</math> | |||
| This can be seen from the definitions of the cross product and dot product, as | |||
| :<math>\begin{align} \mathbf{a} \times \mathbf{b} &= ab \mathbf{n} \sin{\theta} \\ | |||
| \mathbf{a} \cdot \mathbf{b} &= ab \cos{\theta}, \end{align}</math> | |||
| with '''n''' a ] normal to both '''a''' and '''b'''. The relationship follows from these definitions and the Pythagorean trigonometric identity. | |||
| This can also be used to define the cross product. By rearranging the following equation is obtained | |||
| :<math> \|\mathbf{a} \times \mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a} \cdot \mathbf{b})^2.</math> | |||
| This can be considered as a condition on the cross product and so part of its definition, for example in ].<ref name=n_dimensions>{{cite book |title=Clifford algebras and spinors |author=Pertti Lounesto |chapter-url=https://books.google.com/books?id=kOsybQWDK4oC&pg=PA96 |page=96 |chapter=§7.4 Cross product of two vectors |isbn=0-521-00551-5 |year=2001 |publisher=Cambridge University Press |edition=2nd}} | |||
| </ref><ref name=Hildebrand> | |||
| {{cite book |title=Methods of applied mathematics |author=Francis Begnaud Hildebrand |page=24 |url=https://books.google.com/books?id=17EZkWPz_eQC&pg=PA24|isbn=0-486-67002-3 |edition=Reprint of Prentice-Hall 1965 2nd|publisher=Courier Dover Publications |year=1992}} | |||
| </ref> | |||
| ===As an axiom=== | |||
| {{main|Parallel postulate}} | |||
| If the first four of the ] are assumed to be true then the Pythagorean theorem is equivalent to the fifth. That is, ] implies the Pythagorean theorem and vice-versa. | |||
| ==Generalizations== | ==Generalizations== | ||
| ===Similar figures on the three sides=== | ===Similar figures on the three sides=== | ||
| ] | |||
| ] | |||
| The Pythagorean theorem was generalized by ] in his '']'' to extend beyond the areas of squares on the three sides to ]:<ref name=Euclid_VI>Euclid's ''Elements'': Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle."</ref> | |||
| The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any ]. This was known by ] in the 5th century BC,<ref>Heath, T. L., ''A History of Greek Mathematics'', Oxford University Press, 1921; reprinted by Dover, 1981.</ref> and was included by ] in his '']'':<ref name=Euclid_VI>Euclid's ''Elements'': Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle."</ref> | |||
| <blockquote>If one erects similar figures (see ]) on the sides of a right triangle, then the sum of the areas of the two smaller ones equals the area of the larger one.</blockquote> | |||
| <blockquote>If one erects similar figures (see ]) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.</blockquote> | |||
| The basic idea behind this generalization is that the area of a plane figure is ] to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas ''A'', ''B'' and ''C'' are erected on sides with lengths ''a'', ''b'' and ''c'' then: | |||
| This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are ''a:b:c'').<ref name=Putz>Putz, John F. and Sipka, Timothy A. "On generalizing the Pythagorean theorem", ''The College Mathematics Journal'' 34 (4), September 2003, pp. 291–295.</ref> While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).<ref name=Putz/> | |||
| The basic idea behind this generalization is that the area of a plane figure is ] to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas {{mvar|A}}, {{mvar|B}} and {{mvar|C}} are erected on sides with corresponding lengths {{mvar|a}}, {{mvar|b}} and {{mvar|c}} then: | |||
| :<math>\frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2}\, ,</math> | :<math>\frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2}\, ,</math> | ||
| :<math>\Rightarrow A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C\, .</math> | :<math>\Rightarrow A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C\, .</math> | ||
| But, by the Pythagorean theorem, ''a''<sup>2</sup> + ''b''<sup>2</sup> = ''c''<sup>2</sup>, so ''A'' + ''B'' = ''C''. | But, by the Pythagorean theorem, {{math|1=''a''<sup>2</sup> + ''b''<sup>2</sup> = ''c''<sup>2</sup>}}, so {{math|1=''A'' + ''B'' = ''C''}}. | ||
| Conversely, if we can prove that ''A'' + ''B'' = ''C'' for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle |
Conversely, if we can prove that {{math|1=''A'' + ''B'' = ''C''}} for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle {{mvar|C}} on its hypotenuse, and two similar right triangles ({{mvar|A}} and {{mvar|B}} ) constructed on the other two sides, formed by dividing the central triangle by its ]. The sum of the areas of the two smaller triangles therefore is that of the third, thus {{math|1=''A'' + ''B'' = ''C''}} and reversing the above logic leads to the Pythagorean theorem {{math|1=''a''<sup>2</sup> + ''b''<sup>2</sup> = ''c''<sup>2</sup>}}. (''See also ]'') | ||
| {| | |||
| | ] | |||
| | ] | |||
| | ] | |||
| |} | |||
| ===Law of cosines=== | ===Law of cosines=== | ||
| {{main|Law of cosines}} | {{main|Law of cosines}} | ||
| ] is given by the ]. Interior angle Δθ = θ<sub>1</sub>−θ<sub>2</sub>.]] | |||
| The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines:<ref name= Leff1> | |||
| The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that | |||
| <math display="block">a^2+b^2-2ab\cos{\theta}=c^2 </math> | |||
| {{cite book |title=''cited work'' |author=Lawrence S. Leff |url=http://books.google.com/?id=y_7yrqrHTb4C&pg=PA326 |page=326 |isbn=0764128922 |publisher=Barron's Educational Series |date=2005-05-01}} | |||
| where <math>\theta</math> is the angle between sides <math>a</math> and <math>b</math>.<ref name= Leff1> | |||
| {{cite book |title=''cited work'' |author=Lawrence S. Leff |url=https://books.google.com/books?id=y_7yrqrHTb4C&pg=PA326 |page=326 |isbn=0-7641-2892-2 |publisher=Barron's Educational Series |date=2005-05-01}} | |||
| </ref> | </ref> | ||
| :: <math>a^2+b^2-2ab\cos{\theta}=c^2, \,</math> | |||
| where θ is the angle between sides ''a'' and ''b''. | |||
| When |
When <math>\theta</math> is <math>\frac{\pi}{2}</math> radians or 90°, then <math>\cos{\theta} = 0</math>, and the formula reduces to the usual Pythagorean theorem. | ||
| ===Arbitrary triangle=== | ===Arbitrary triangle=== | ||
| ].<ref name=Eves> | ].<ref name=Eves> | ||
| {{cite book |title=Great moments in mathematics (before 1650) |author=Howard Whitley Eves |url= |
{{cite book |title=Great moments in mathematics (before 1650) |author=Howard Whitley Eves |url=https://archive.org/details/greatmomentsinma0007eves |url-access=registration |chapter=§4.8:...generalization of Pythagorean theorem |isbn=0-88385-310-8 |year=1983 |page= |publisher=Mathematical Association of America}} | ||
| </ref> Lower panel: reflection of triangle |
</ref> Lower panel: reflection of triangle CAD (top) to form triangle DAC, similar to triangle ABC (top).]] | ||
| At any selected angle of a general triangle of sides ''a, b, c'', inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled |
At any selected angle of a general triangle of sides ''a, b, c'', inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled {{mvar|c}}. Inscribing the isosceles triangle forms triangle ''CAD'' with angle θ opposite side {{mvar|b}} and with side {{mvar|r}} along {{mvar|c}}. A second triangle is formed with angle θ opposite side {{mvar|a}} and a side with length {{mvar|s}} along {{mvar|c}}, as shown in the figure. ] stated that the sides of the three triangles were related as:<ref name=Sayii> | ||
| {{cite journal |doi=10.1086/348837 |jstor=227603 |author=Aydin Sayili |date=Mar 1960 |title= Thâbit ibn Qurra's Generalization of the Pythagorean Theorem |journal= Isis |volume= 51 |issue=1 |pages= 35–37 |s2cid=119868978 }}</ref><ref name=Sally2> | |||
| </ref> stated that the sides of the three triangles were related as:<ref name=Sayii> | |||
| {{cite book |title=Roots to Research: A Vertical Development of Mathematical Problems |author1=Judith D. Sally |author2=Paul Sally |chapter=Exercise 2.10 (ii) |page=62 |chapter-url=https://books.google.com/books?id=nHxBw-WlECUC&pg=PA62 | |||
| {{cite journal |doi=10.1086/348837 |url=http://www.jstor.org/stable/227603 | |||
| |isbn=978-0-8218-4403-8 |date=2007-12-21 |publisher=American Mathematical Soc. }} | |||
| |author=Aydin Sayili |year= 1960 |title= Thâbit ibn Qurra's Generalization of the Pythagorean Theorem |journal= Isis |volume= 51 |issue=1 |pages= 35–37 |month=Mar. |ref=harv}}</ref><ref name=Sally2> | |||
| {{cite book |title=Cited work |author=Judith D. Sally, Paul Sally |chapter=Exercise 2.10 (ii) |page=62 |url=http://books.google.com/books?id=nHxBw-WlECUC&pg=PA62 | |||
| |isbn=0821844032 |date=2007-12-21 }} | |||
| </ref> | </ref> | ||
| :<math> a^2 +b^2 =c(r+s) \ . </math> | :<math> a^2 +b^2 =c(r+s) \ . </math> | ||
| As the angle θ approaches |
As the angle θ approaches {{pi}}/2, the base of the isosceles triangle narrows, and lengths {{mvar|r}} and {{mvar|s}} overlap less and less. When {{math|1=''θ'' = {{pi}}/2}}, ''ADB'' becomes a right triangle, {{math|1=''r'' + ''s'' = ''c''}}, and the original Pythagorean theorem is regained. | ||
| One proof observes that triangle ''ABC'' has the same angles as triangle '' |
One proof observes that triangle ''ABC'' has the same angles as triangle ''CAD'', but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the ].) Consequently, ''ABC'' is similar to the reflection of ''CAD'', the triangle ''DAC'' in the lower panel. Taking the ratio of sides opposite and adjacent to θ, | ||
| :<math>\frac{c}{ |
:<math>\frac{c}{b} = \frac{b}{r} \ .</math> | ||
| Likewise, for the reflection of the other triangle, | Likewise, for the reflection of the other triangle, | ||
| :<math>\frac{c}{ |
:<math>\frac{c}{a} = \frac{a}{s} \ . </math> | ||
| Clearing fractions and adding these two relations: | ] and adding these two relations: | ||
| :<math> |
:<math> cs + cr = a^2 +b^2 \ , </math> | ||
| the required result. | the required result. | ||
| The theorem remains valid if the angle <math> \theta </math> is obtuse so the lengths {{mvar|r}} and {{mvar|s}} are non-overlapping. | |||
| ===General triangles using parallelograms=== | ===General triangles using parallelograms=== | ||
| ] | ] | ||
| ] | ] | ||
| ] is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras' theorem, and was considered a generalization by ] in 4 AD<ref name=Jennings>For the details of such a construction, see {{cite book |title=Modern geometry with applications: with 150 figures |first=George |last=Jennings |chapter=Figure 1.32: The generalized Pythagorean theorem |page= |url=https://archive.org/details/moderngeometrywi0000jenn |url-access=registration |isbn=0-387-94222-X |year=1997 |edition=3rd |publisher=Springer}}</ref><ref>Claudi Alsina, Roger B. Nelsen: ''Charming Proofs: A Journey Into Elegant Mathematics''. MAA, 2010, {{isbn|9780883853481}}, pp. 77–78 ({{Google books|mIT5-BN_L0oC|excerpt|page=77}})</ref> | |||
| A further generalization applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares.<ref name=Jennings> | |||
| The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base {{mvar|b}} and height {{mvar|h}}. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms. | |||
| For the details of such a construction, see {{cite book |title=Modern geometry with applications: with 150 figures |author=George Jennings |chapter=Figure 1.32: The generalized Pythagorean theorem |page=23 |url=http://books.google.com/?id=6OhcE7YQY8QC&pg=PA23 |isbn=038794222X |year=1997 |edition=3rd |publisher=Springer}} | |||
| ===Solid geometry=== | |||
| </ref> (Squares are a special case, of course.) The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras' theorem, and was considered a generalization by ] in 4 A.D.<ref name=Jennings/> | |||
| ] | |||
| ] | |||
| In terms of ], Pythagoras' theorem can be applied to three dimensions as follows. Consider the ] shown in the figure. The length of ] ''AC'' is found from Pythagoras' theorem as: | |||
| The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base ''b'' and height ''h''. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms. | |||
| :<math> \overline{AC}^{\,2} = \overline{AB}^{\,2} + \overline{BC}^{\,2} \, ,</math> | |||
| ===Complex arithmetic=== | |||
| {{main|Complex arithmetic}} | |||
| Pythagoras' formula is used to find the distance between two points in the ] coordinate plane, and is valid if all coordinates are real: the distance ''s'' between the points (''a'', ''b'') and (''c'', ''d'') is | |||
| :<math>s = \sqrt{(a-c)^2 + (b-d)^2}.\ </math> | |||
| where these three sides form a right triangle. Using diagonal ''AC'' and the horizontal edge ''CD'', the length of ] ''AD'' then is found by a second application of Pythagoras' theorem as: | |||
| No problem arises with the formula if ] are treated as vectors with real components as in {{nowrap|''x'' + ''i y'' {{=}} (''x'', ''y'').}} For example, the distance ''s'' between {{nowrap|0 + 1''i''}} and {{nowrap|1 + 0''i''}} becomes the magnitude of the vector {{nowrap|(0, 1) − (1, 0) {{=}} (−1, 1),}} or | |||
| :<math> s = \sqrt{ (-1)^2 +1^2} = \sqrt{2}.\ </math> | |||
| :<math> \overline{AD}^{\,2} = \overline{AC}^{\,2} + \overline{CD}^{\,2} \, ,</math> | |||
| However, a modification of the Pythagorean formula is necessary for a direct treatment of vectors with ]. The distance between the points with complex coordinates {{nowrap|(''a'', ''b'')}} and {{nowrap|(''c'', ''d'');}} ''a'', ''b'', ''c'', and ''d'' all complex; is formulated using ]. The distance ''s'' is based upon the vector difference {{nowrap|(''a'' − ''c'', ''b'' − ''d'') }} in the following manner:<ref name=Brown> | |||
| {{cite book |title=An introduction to analysis |author=Arlen Brown, Carl M. Pearcy |url=http://books.google.com/books?id=Y2Mwck8Q9A4C&pg=PA124 |page=124 |chapter=Item ''C'': Norm for an arbitrary ''n''-tuple ... |isbn=0387943692 |publisher=Springer |year=1995}} See also pages 47–50. | |||
| </ref> Let the difference ''a'' − ''c'' = ''p'' + i ''q'', where ''p'' is the real part of the difference, ''q'' is the imaginary part and i = √(−1). Likewise, let ''b'' − ''d'' = ''r'' + i''s''. Then: | |||
| :<math> | |||
| \begin{align} | |||
| s &= \sqrt{(p+iq)\overline{(p+iq)} + (r+is)\overline{(r+is)}} \\ | |||
| &= \sqrt{(p+iq)(p-iq) + (r+is)(r-is)} \\ | |||
| &= \sqrt{p^2 + q^2 + r^2 + s^2}, | |||
| \end{align} | |||
| </math> | |||
| where <math>\overline{\mathit z}</math> is the ] of <math>\mathit z\ </math>. | |||
| For example, the distance between the points {{nowrap|(''a'', ''b'') {{=}} (0, 1)}} and {{nowrap|(''c'', ''d'') {{=}} (''i'', 0)}} begins with the difference {{nowrap|(''a'' − ''c'', ''b'' − ''d'') {{=}} (−''i'', 1)}} and would work out as 0 if complex conjugates were not taken. Using the modified formula, the result is | |||
| : <math>s = \sqrt{(-i)\cdot(\overline{-i}) + 1 \cdot\overline{1}}= \sqrt{(-i)\cdot{i} + 1 \cdot{1}} = \sqrt{2}. \, </math> | |||
| The norm defined by: | |||
| :<math>\|\mathbf p \| = \sqrt{\mathbf {p \cdot \overline{p}}} = \sqrt{|p_1|^2 + |p_2|^2 + \dots +|p_n|^2} \ , </math> | |||
| is a ].<ref name=Gray> | |||
| {{cite book |title=Modern differential geometry of curves and surfaces with Mathematica |author=Alfred Gray, Elsa Abbena, Simon Salamon |page=194 |url=http://books.google.com/?id=TGw98Z6Cv-EC&pg=PA194 |isbn=1584884487 |year=2006 |publisher=CRC Press |edition =3rd}} | |||
| </ref> | |||
| ===Solid geometry=== | |||
| {{main|Solid geometry}} | |||
| ] | |||
| ] | |||
| In terms of solid geometry, Pythagoras' theorem can be applied to three dimensions as follows. Consider a rectangular solid as shown in the figure. The length of diagonal ''BD'' is found from Pythagoras' theorem as: | |||
| :<math> \overline{BD}^{\,2} = \overline{BC}^{\,2} + \overline{CD}^{\,2} \ ,</math> | |||
| where these three sides form a right triangle. Using horizontal diagonal ''BD'' and the vertical edge ''AB'', the length of diagonal ''AD'' then is found by a second application of Pythagoras' theorem as: | |||
| :<math> \overline{AD}^{\,2} = \overline{AB}^{\,2} + \overline{BD}^{\,2} \ ,</math> | |||
| or, doing it all in one step: | or, doing it all in one step: | ||
| :<math> \overline{AD}^{\,2} = \overline{AB}^{\,2} + \overline{BC}^{\,2} + \overline{CD}^{\,2} |
:<math> \overline{AD}^{\,2} = \overline{AB}^{\,2} + \overline{BC}^{\,2} + \overline{CD}^{\,2} \, .</math> | ||
| This result is the three-dimensional expression for the magnitude of a vector '''v''' (the diagonal AD) in terms of its orthogonal components {'''v'''<sub>k</sub>} (the three mutually perpendicular sides): | This result is the three-dimensional expression for the magnitude of a vector '''v''' (the diagonal AD) in terms of its orthogonal components {{math|{{mset|'''v'''<sub>k</sub>}}}} (the three mutually perpendicular sides): | ||
| :<math>\|\mathbf{v}\|^2 = \sum_{k=1}^3 \|\mathbf{v}_k\|^2.</math> | :<math>\|\mathbf{v}\|^2 = \sum_{k=1}^3 \|\mathbf{v}_k\|^2.</math> | ||
| Line 507: | Line 454: | ||
| This one-step formulation may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem to a succession of right triangles in a sequence of orthogonal planes. | This one-step formulation may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem to a succession of right triangles in a sequence of orthogonal planes. | ||
| A substantial generalization of the Pythagorean theorem to three dimensions is ], named for ]: If a ] has a right angle corner (a corner |
A substantial generalization of the Pythagorean theorem to three dimensions is ], named for ]: If a ] has a right angle corner (like a corner of a ]), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the "{{mvar|n}}-dimensional Pythagorean theorem":<ref name=Bhatia> | ||
| {{cite book |title=Matrix analysis |author=Rajendra Bhatia |url=https://books.google.com/books?id=eay3HALl620C&pg=PA21 |page=21 |isbn=0-387-94846-5 |year=1997 |publisher=Springer}}</ref> | |||
| {{Blockquote|text=Let <math>x_1, x_2, \ldots,x_n </math> be orthogonal vectors in {{math|'''R'''<sup>''n''</sup>}}. Consider the {{mvar|n}}-dimensional simplex {{mvar|S}} with vertices <math>0,x_1,\ldots, x_n</math>. (Think of the {{math|(''n'' − 1)}}-dimensional simplex with vertices <math>x_1,\ldots,x_n</math> not including the origin as the "hypotenuse" of {{mvar|S}} and the remaining {{math|(''n'' − 1)}}-dimensional faces of {{mvar|S}} as its "legs".) Then the square of the volume of the hypotenuse of {{mvar|S}} is the sum of the squares of the volumes of the {{mvar|n}} legs.}} | |||
| {{cite book |title=Matrix analysis |author=Rajendra Bhatia |url=http://books.google.com/?id=eay3HALl620C&pg=PA21 |page=21 |isbn=0387948465 |year=1997 |publisher=Springer}} | |||
| </ref> | |||
| {{Blockquote|text=Let <math>x_1, x_2, ...x_n \,</math> be orthogonal vectors in ℝ<sup>n</sup>. Consider the ''n''-dimensional simplex ''S'' with vertices <math>0,x_1 ... x_n\,</math>. (Think of the (''n''−1) dimensional simplex with vertices <math>x_1,...x_n\,</math> not including the origin as the "hypotenuse" of ''S'' and the remaining (''n''−1)-dimensional faces of ''S'' as its "legs".) Then the square of the volume of the hypotenuse of ''S'' is the sum of the squares of the volumes of the ''n'' legs.}} | |||
| This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different wording:<ref name=Wong> | This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different wording:<ref name=Wong> | ||
| For an extended discussion of this generalization, see, for example, {{Webarchive|url=https://web.archive.org/web/20091229111557/http://www.dpmms.cam.ac.uk/~ww278/papers/gp.pdf |date=2009-12-29 }} 2002, ''A generalized n-dimensional Pythagorean theorem''. | |||
| For an extended discussion of this generalization, see, for example, 2002, ''A generalized n-dimensional Pythagorean theorem''. | |||
| </ref> | </ref> | ||
| {{blockquote|text=Given an |
{{blockquote|text=Given an {{mvar|n}}-rectangular {{mvar|n}}-dimensional simplex, the square of the {{math|(''n'' − 1)}}-content of the ] opposing the right vertex will equal the sum of the squares of the {{math|(''n'' − 1)}}-contents of the remaining facets.}} | ||
| ===Inner product spaces=== | ===Inner product spaces=== | ||
| ] | |||
| {{See also|Hilbert space}} | |||
| ] | |||
| The Pythagorean theorem can be generalized to ]s,<ref name=van_der_Heijden> | The Pythagorean theorem can be generalized to ]s,<ref name=van_der_Heijden> | ||
| {{cite book |title=Classification, parameter estimation, and state estimation | |
{{cite book |title=Classification, parameter estimation, and state estimation |author1=Ferdinand van der Heijden |author2=Dick de Ridder |url=https://books.google.com/books?id=krSB9PIKMSYC&pg=PA357 |page=357 |isbn=0-470-09013-8 |year=2004 |publisher=Wiley}} | ||
| </ref> which are generalizations of |
</ref> which are generalizations of the familiar 2-dimensional and 3-dimensional ]. For example, a ] may be considered as a ] with infinitely many components in an inner product space, as in ].<ref name=Lin> | ||
| {{cite book |title=Finite element methods: accuracy and improvement | |
{{cite book |title=Finite element methods: accuracy and improvement |author1=Qun Lin |author2=Jiafu Lin |url=https://books.google.com/books?id=cMvAqzMuAWgC&pg=PA23 |page=23 |isbn=7-03-016656-6 |year=2006 |publisher=Elsevier}} | ||
| </ref> | </ref> | ||
| Line 535: | Line 478: | ||
| In an inner product space, the concept of ]ity is replaced by the concept of ]ity: two vectors '''v''' and '''w''' are orthogonal if their inner product <math> \langle \mathbf{v} , \mathbf{w}\rangle </math> is zero. The ] is a generalization of the ] of vectors. The dot product is called the ''standard'' inner product or the ''Euclidean'' inner product. However, other inner products are possible.<ref name=Rorres> | In an inner product space, the concept of ]ity is replaced by the concept of ]ity: two vectors '''v''' and '''w''' are orthogonal if their inner product <math> \langle \mathbf{v} , \mathbf{w}\rangle </math> is zero. The ] is a generalization of the ] of vectors. The dot product is called the ''standard'' inner product or the ''Euclidean'' inner product. However, other inner products are possible.<ref name=Rorres> | ||
| {{cite book |title=Elementary Linear Algebra: Applications Version | |
{{cite book |title=Elementary Linear Algebra: Applications Version |author1=Howard Anton |author2=Chris Rorres |url=https://books.google.com/books?id=1PJ-WHepeBsC&pg=PA336 |page=336 |isbn=978-0-470-43205-1 |year=2010 |edition=10th |publisher=Wiley}} | ||
| </ref> | </ref> | ||
| The concept of length is replaced by the concept of the ] |
The concept of length is replaced by the concept of the ] ‖'''v'''‖ of a vector '''v''', defined as:<ref name=Saxe> | ||
| {{cite book |title=Beginning functional analysis |author=Karen Saxe |url= |
{{cite book |title=Beginning functional analysis |author=Karen Saxe|author-link= Karen Saxe |chapter-url=https://books.google.com/books?id=QALoZC64ea0C&pg=PA7 |page=7 |chapter=Theorem 1.2 |isbn=0-387-95224-1 |year=2002 |publisher=Springer}} | ||
| </ref> | </ref> | ||
| :<math>\lVert \mathbf{v} \rVert |
:<math>\lVert \mathbf{v} \rVert \equiv \sqrt{\langle \mathbf{v},\mathbf{v}\rangle} \, .</math> | ||
| In |
In an inner-product space, the '''Pythagorean theorem''' states that for any two orthogonal vectors '''v''' and '''w''' we have | ||
| :<math>\left\| \mathbf{v} + \mathbf{w} \right\|^2 = \left\| \mathbf{v} |
:<math>\left\| \mathbf{v} + \mathbf{w} \right\|^2 = \left\| \mathbf{v} \right\|^2 + \left\| \mathbf{w} \right\|^2 .</math> | ||
| Here the vectors |
Here the vectors '''v''' and '''w''' are akin to the sides of a right triangle with hypotenuse given by the ] '''v''' + '''w'''. This form of the Pythagorean theorem is a consequence of the ]: | ||
| :<math>\begin{align} | |||
| :<math>\left\| \mathbf{v} + \mathbf{w} \right\|^2 =\langle \mathbf{ v+w},\ \mathbf{ v+w}\rangle = \langle \mathbf{ v},\ \mathbf{ v}\rangle +\langle \mathbf{ w},\ \mathbf{ w}\rangle +\langle\mathbf{ v,\ w }\rangle + \langle\mathbf{ w,\ v }\rangle \ = \left\| \mathbf{v}\right\|^2 + \left\| \mathbf{w}\right\|^2, </math> | |||
| \left\| \mathbf{v} + \mathbf{w} \right\|^2 | |||
| where the inner products of the cross terms are zero by orthogonality. | |||
| &= \langle \mathbf{ v+w},\ \mathbf{ v+w}\rangle \\ | |||
| &= \langle \mathbf{ v},\ \mathbf{ v}\rangle +\langle \mathbf{ w},\ \mathbf{ w}\rangle +\langle\mathbf{ v,\ w }\rangle + \langle\mathbf{ w,\ v }\rangle \\ | |||
| &= \left\| \mathbf{v}\right\|^2 + \left\| \mathbf{w}\right\|^2, | |||
| \end{align}</math> | |||
| where <math>\langle\mathbf{ v,\ w }\rangle = \langle\mathbf{ w,\ v }\rangle = 0</math> because of orthogonality. | |||
| A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the ] :<ref name=Saxe/> | A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the '']'':<ref name=Saxe/> | ||
| :<math>2\|\mathbf v\|^2 +2 \|\mathbf w\|^2 = \|\mathbf {v + w} \|^2 +\| \mathbf{v-w}\|^2 \ , </math> | :<math>2\|\mathbf v\|^2 +2 \|\mathbf w\|^2 = \|\mathbf {v + w} \|^2 +\| \mathbf{v-w}\|^2 \ , </math> | ||
| Line 558: | Line 506: | ||
| which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is '']'' a norm corresponding to an inner product.<ref name=Saxe/> | which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is '']'' a norm corresponding to an inner product.<ref name=Saxe/> | ||
| {{anchor|Decomposition}} | |||
| The identity can be extended to sums of more than two vectors. If '''v'''<sub>''1''</sub>, '''v'''<sub>''2''</sub>, ..., '''v'''<sub>''n''</sub> are pairwise-orthogonal vectors in an inner product space, application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on ]) results in the equation<ref name='Douglas1998'>{{cite book | last = Douglas | first = Ronald G. | title = Banach Algebra Techniques in Operator Theory, 2nd edition | publisher = Springer-Verlag New York, Inc | year = 1998 | location = New York, New York | pages = 60–1 | url = http://books.google.com/?id=-OdfXeNmrT0C&pg=PA60#v=onepage&q | isbn = 978-0387983776}}</ref> | |||
| The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If '''v'''<sub>1</sub>, '''v'''<sub>2</sub>, ..., '''v'''<sub>{{mvar|n}}</sub> are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on ]) results in the equation<ref name='Douglas1998'>{{cite book | last = Douglas | first = Ronald G. | title = Banach Algebra Techniques in Operator Theory | edition = 2nd | publisher = Springer-Verlag New York, Inc. | year = 1998 | location = New York, New York | pages = 60–61 | url = https://books.google.com/books?id=-OdfXeNmrT0C&pg=PA60 | isbn = 978-0-387-98377-6}}</ref> | |||
| :<math>\|\sum_{k=1}^{n}\mathbf{v}_k\|^2 = \sum_{k=1}^n \|\mathbf{v}_k\|^2.</math> | |||
| :<math>\biggl\|\sum_{k=1}^n\mathbf{v}_k\biggr\|^2=\sum_{k=1}^n\|\mathbf{v}_k\|^2</math> | |||
| ] is a further generalization that considers infinite sums of orthogonal vectors. | |||
| ===Sets of ''m''-dimensional objects in ''n''-dimensional space=== | |||
| ===Non-Euclidean geometry=== | |||
| {{main|Non-Euclidean geometry}} | |||
| {{See also|Hilbert's axioms}} | |||
| The Pythagorean theorem is derived from the axioms of ], and in fact, the Pythagorean theorem given above does not hold in a ].<ref name=false> | |||
| Another generalization of the Pythagorean theorem applies to ] sets of objects in any number of dimensions. Specifically, the square of the measure of an {{mvar|m}}-dimensional set of objects in one or more parallel {{mvar|m}}-dimensional ] in {{mvar|n}}-dimensional ] is equal to the sum of the squares of the measures of the ] projections of the object(s) onto all {{mvar|m}}-dimensional coordinate subspaces.<ref name=Conant> | |||
| {{cite book |title=''cited work'' |author=Stephen W. Hawking |page=4 |url=http://books.google.com/books?id=3zdFSOS3f4AC&pg=PA4 |isbn=0762419229 |year=2005}} | |||
| {{cite journal |doi=10.2307/2319528 |title=Generalized Pythagorean Theorem |author1=Donald R Conant |author2=William A Beyer |name-list-style=amp |journal=The American Mathematical Monthly |volume=81 |date=Mar 1974 |pages=262–265 |jstor=2319528 |issue=3 |publisher=Mathematical Association of America }} | |||
| </ref> | |||
| In mathematical terms: | |||
| </ref> (The Pythagorean theorem has been shown, in fact, to be ].<ref name=Parallel> | |||
| :<math>\mu^2_{ms} = \sum_{i=1}^{x}\mathbf{\mu^2}_{mp_i}</math> | |||
| where: | |||
| * <math>\mu_m</math> is a measure in {{mvar|m}}-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.). | |||
| * <math>s</math> is a set of one or more non-overlapping {{mvar|m}}-dimensional objects in one or more parallel {{mvar|m}}-dimensional flats in {{mvar|n}}-dimensional Euclidean space. | |||
| * <math>\mu_{ms}</math> is the total measure (sum) of the set of {{mvar|m}}-dimensional objects. | |||
| * <math>p</math> represents an {{mvar|m}}-dimensional projection of the original set onto an orthogonal coordinate subspace. | |||
| * <math>\mu_{mp_i}</math> is the measure of the {{mvar|m}}-dimensional set projection onto {{mvar|m}}-dimensional coordinate subspace <math>i</math>. Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace. | |||
| * <math>x</math> is the number of orthogonal, {{mvar|m}}-dimensional coordinate subspaces in {{mvar|n}}-dimensional space ({{math|'''R'''<sup>''n''</sup>}}) onto which the {{mvar|m}}-dimensional objects are projected {{math|(''m'' ≤ ''n'')}}: <math display="block">x = \binom{n}{m} = \frac{n!}{m!(n-m)!}</math> | |||
| ===Non-Euclidean geometry=== | |||
| The Pythagorean theorem is derived from the ] of ], and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem ].<ref name=Parallel> | |||
| {{cite book |title=CRC concise encyclopedia of mathematics |author= Eric W. Weisstein |url= |
{{cite book |title=CRC concise encyclopedia of mathematics |author= Eric W. Weisstein |url=https://books.google.com/books?id=aFDWuZZslUUC&pg=PA2147 |page=2147 |quote=The parallel postulate is equivalent to the ''Equidistance postulate'', ''Playfair axiom'', ''Proclus axiom'', the ''Triangle postulate'' and the ''Pythagorean theorem''. |edition=2nd |isbn=1-58488-347-2 |year=2003|publisher= CRC Press }} | ||
| </ref><ref name= Pruss> | </ref><ref name= Pruss> | ||
| {{cite book |title=The principle of sufficient reason: a reassessment |author= Alexander R. Pruss |quote=We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate. |isbn= |
{{cite book |title=The principle of sufficient reason: a reassessment |author= Alexander R. Pruss |quote=We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate. |isbn=0-521-85959-X |year=2006 |publisher=Cambridge University Press |page=11 |url=https://books.google.com/books?id=8qAxk1rXIjQC&pg=PA11}} | ||
| </ref> Thus, right triangles in a ]<ref name=false> | |||
| </ref>) | |||
| In other words, in non-Euclidean geometry, the relation between the sides of a triangle must necessarily take a non-Pythagorean form. For example, in ], all three sides of the right triangle (say ''a'', ''b'', and ''c'') bounding an octant of the unit sphere have length equal to π/2, which violates the Pythagorean theorem because {{nowrap|''a''<sup>2</sup> + ''b''<sup>2</sup> ≠ ''c''<sup>2</sup>.}} | |||
| {{cite book |title=''cited work'' |author=Stephen W. Hawking |page=4 |url=https://books.google.com/books?id=3zdFSOS3f4AC&pg=PA4 |isbn=0-7624-1922-9 |year=2005|publisher=Running Press }} | |||
| Here two cases of non-Euclidean geometry are considered—] and ]; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines. | |||
| ====Spherical geometry==== | |||
| {{main|Spherical geometry}} | |||
| ] | |||
| For any right triangle on a sphere of radius ''R'' (for example, if γ in the figure is a right angle), with sides ''a'', ''b'', ''c'', the relation between the sides takes the form:<ref name=O'Neill> | |||
| {{cite book |title=Elementary differential geometry |author=Barrett O'Neill |url=http://books.google.com/?id=OtbNXAIve_AC&pg=PA441 |chapter=Exercise 4 |page=441 |isbn=0120887355 |year=2006 |edition=2nd |publisher=Academic Press}} | |||
| </ref> | </ref> | ||
| do not satisfy the Pythagorean theorem. For example, in ], all three sides of the right triangle (say {{mvar|a}}, {{mvar|b}}, and {{mvar|c}}) bounding an octant of the unit sphere have length equal to {{pi}}/2, and all its angles are right angles, which violates the Pythagorean theorem because | |||
| <math> a^2 + b^2 = 2 c^2 > c^2 </math>. | |||
| Here two cases of non-Euclidean geometry are considered—] and ]; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines. | |||
| :<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\cos \left(\frac{b}{R}\right).</math> | |||
| However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say {{math|1=''A''+''B'' = ''C''}}. The sides are then related as follows: the sum of the areas of the circles with diameters {{mvar|a}} and {{mvar|b}} equals the area of the circle with diameter {{mvar|c}}.<ref> | |||
| This equation can be derived as a special case of the ] that applies to all spherical triangles: | |||
| {{cite journal|author=Victor Pambuccian|title=Maria Teresa Calapso's Hyperbolic Pythagorean Theorem|journal=The Mathematical Intelligencer|volume=32|date=December 2010|page =2|doi=10.1007/s00283-010-9169-0|issue=4|doi-access=free}} | |||
| :<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right)\cos \left(\frac{b}{R}\right) +\sin\left(\frac{a}{R}\right) \sin\left(\frac{b}{R}\right) \cos \gamma \ .</math> | |||
| </ref> | |||
| By using the ] for the cosine function, {{nowrap|cos ''x'' ≈ 1 − ''x''<sup>2</sup>/2}}, it can be shown that as the radius ''R'' approaches infinity and the arguments ''a/R, b/R and c/R'' tend to zero, the spherical relation between the sides of a right triangle approaches the form of Pythagoras' theorem. Substituting the approximate quadratic for each of the cosines in the spherical relation for a right triangle: | |||
| :<math>1-\left(\frac{c}{R}\right)^2= \left\left + \ \mathrm{higher\ order\ terms} </math> | |||
| Multiplying out the bracketed quantities, Pythagoras' theorem is recovered for large radii ''R'': | |||
| :<math>\left(\frac{c}{R}\right)^2= \left(\frac{a}{R}\right)^2 + \left(\frac{b}{R}\right)^2 + \ \mathrm{higher\ order\ terms} \ ,</math> | |||
| where the ] become negligibly small as ''R'' becomes large. | |||
| ==== |
====Spherical geometry==== | ||
| ] | |||
| {{main|Hyperbolic geometry}} | |||
| For any right ] of radius {{math|''R''}} (for example, if {{math|γ}} in the figure is a right angle), with sides {{math|''a'', ''b'', ''c'',}} the relation between the sides takes the form:<ref name=O>{{cite book |title=Elementary Differential Geometry |author=Barrett O'Neill |chapter-url=https://books.google.com/books?id=OtbNXAIve_AC&pg=PA441 |chapter=Exercise 4 |page=441 |isbn=0-12-088735-5 |year=2006 |edition=2nd |publisher=Academic Press}}</ref> | |||
| {{See also|Gaussian curvature}} | |||
| ] | |||
| For a right triangle in hyperbolic geometry with sides ''a'', ''b'', ''c'' and with side ''c'' opposite a right angle, the relation between the sides takes the form:<ref name=Stahl> | |||
| :<math> \cos{\frac cR} = \cos{\frac aR} \, \cos{\frac bR}.</math> | |||
| {{cite book |title=The Poincaré half-plane: a gateway to modern geometry |author=Saul Stahl |page=122 |url=http://books.google.com/?id=TABicHVMQhMC&pg=PA122 |chapter=Theorem 8.3| isbn=086720298X |year=1993 |publisher=Jones & Bartlett Learning}} | |||
| This equation can be derived as a special case of the ] that applies to all spherical triangles: | |||
| </ref> | |||
| :<math> \ |
:<math> \cos{\frac cR} = \cos{\frac aR} \, \cos{\frac bR} + \sin{\frac aR} \, \sin{\frac bR} \, \cos{\gamma}.</math> | ||
| For infinitesimal triangles on the sphere (or equivalently, for finite spherical triangles on a sphere of infinite radius), the spherical relation between the sides of a right triangle reduces to the Euclidean form of the Pythagorean theorem. To see how, assume we have a spherical triangle of fixed side lengths {{math|''a'', ''b'',}} and {{mvar|c}} on a sphere with expanding radius {{math|''R''}}. As {{math|''R''}} approaches infinity the quantities {{math|''a/R'', ''b/R'',}} and {{math|''c/R''}} tend to zero and the spherical Pythagorean identity reduces to <math>1 = 1,</math> so we must look at its ]. | |||
| where cosh is the ]. This formula is a special form of the ] that applies to all hyperbolic triangles:<ref name=Gilman> | |||
| The ] for the cosine function can be written as <math display=inline> \cos x = 1 - \tfrac12 x^2 + O{\left(x^4\right)}</math> with the remainder term in ]. Letting <math>x = c/R</math> be a side of the triangle, and treating the expression as an asymptotic expansion in terms of {{mvar|R}} for a fixed {{mvar|c}}, | |||
| {{cite book |title=Two-generator discrete subgroups of PSL(2,R) |author=Jane Gilman |url=http://books.google.com/?id=YRFz9Zj_vAAC&pg=PA74 |chapter=Hyperbolic triangles |isbn=0821803611 |year=1995 |publisher=American Mathematical Society Bookstore}} | |||
| :<math>\begin{align} | |||
| </ref> | |||
| \cos{\frac cR} = 1 - \frac{c^2}{2R^2} + O{\left(R^{-4}\right)} | |||
| \end{align}</math> | |||
| and likewise for {{math|''a''}} and {{math|''b''}}. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields | |||
| :<math>\cosh c = \cosh a \ \cosh b - \sinh a \ \sinh b \ \cos \gamma \ , </math> | |||
| :<math>\begin{align} | |||
| with γ the angle at the vertex opposite the side ''c''. | |||
| 1-\frac{c^2}{2R^2} + O{\left(R^{-4}\right)} | |||
| &= \left(1-\frac{a^2}{2R^2} + O{\left(R^{-4}\right)} \right) | |||
| \left(1-\frac{b^2}{2R^2} + O{\left(R^{-4}\right)} \right) \\ | |||
| &= 1 - \frac{a^2}{2R^2} - \frac{b^2}{2R^2} + O{\left(R^{-4}\right)}. | |||
| \end{align}</math> | |||
| Subtracting 1 and then negating each side, | |||
| By using the ] for the hyperbolic cosine, {{nowrap|cosh ''x'' ≈ 1 + ''x''<sup>2</sup>/2}}, it can be shown that as a hyperbolic triangle becomes very small (that is, as ''a'', ''b'', and ''c'' all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras' theorem. | |||
| :<math>\frac{c^2}{2R^2} = \frac{a^2}{2R^2} + \frac{b^2}{2R^2} + O{\left(R^{-4}\right)}.</math> | |||
| ===Differential geometry=== | |||
| {{main|Differential geometry}} | |||
| ] (top) and ] (bottom), as given by Pythagoras' theorem]] | |||
| On an infinitesimal level, in three dimensional space, Pythagoras' theorem describes the distance between two infinitesimally separated points as: | |||
| Multiplying through by {{math|2''R''<sup>2</sup>,}} the asymptotic expansion for {{mvar|c}} in terms of fixed {{math|''a'', ''b''}} and variable {{mvar|R}} is | |||
| :<math>ds^2 = dx^2 + dy^2 +dz^2,\, </math> | |||
| :<math>c^2 = a^2 + b^2 + O{\left(R^{-2}\right)}.</math> | |||
| The Euclidean Pythagorean relationship <math display=inline>c^2 = a^2 + b^2</math> is recovered in the limit, as the remainder vanishes when the radius {{mvar|R}} approaches infinity. | |||
| with ''ds'' the element of distance and (''dx'', ''dy'', ''dz'') the components of the vector separating the two points. Such a space is called a ]. However, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:<ref name=Chow> | |||
| {{cite book |title=Mathematical methods for physicists: a concise introduction |author=Tai L. Chow |page=52 |url=http://books.google.com/?id=MpRXPOYZzfUC&pg=PA52 |isbn=0521655447 |year=2000 |publisher=Cambridge University Press}} | |||
| </ref> | |||
| For practical computation in spherical trigonometry with small right triangles, cosines can be replaced with sines using the double-angle identity <math>\cos{2\theta} = 1 - 2\sin^2{\theta}</math> to avoid ]. Then the spherical Pythagorean theorem can alternately be written as | |||
| :<math>ds^2 = \sum_{i,j}^n g_{ij}\, dx_i\, dx_j </math> | |||
| :<math> | |||
| where {{nowrap|''g''<sub>''ij''</sub>}} is called the ]. It may be a function of position. Such ]s include ] as a general example. This formulation also applies to a Euclidean space when using ]. For example, in ]: | |||
| \sin^2{\frac c{2R}} | |||
| = \sin^2{\frac a{2R}} + \sin^2{\frac b{2R}} - 2 \sin^2{\frac a{2R}} \, \sin^2{\frac b{2R}}. | |||
| </math> | |||
| ====Hyperbolic geometry==== | |||
| :<math>ds^2 = dr^2 + r^2 d\theta^2 \ . </math> | |||
| ] ]] | |||
| In a ] space with uniform ] {{math|−1/''R''<sup>2</sup>}}, for a right ] with legs {{mvar|a}}, {{mvar|b}}, and hypotenuse {{mvar|c}}, the relation between the sides takes the form:<ref name=Stahl> | |||
| ===Relation to cross product=== | |||
| ] | |||
| {{See also|Seven-dimensional cross product}} | |||
| Pythagoras' theorem connects two expressions for the magnitude of the cross product. | |||
| {{cite book |title=The Poincaré half-plane: a gateway to modern geometry |author=Saul Stahl |page=122 |chapter-url=https://books.google.com/books?id=TABicHVMQhMC&pg=PA122 |chapter=Theorem 8.3| isbn=0-86720-298-X |year=1993 |publisher=Jones & Bartlett Learning}} | |||
| One approach to defining a ] is to require that it satisfies the equation,<ref name=Massey> | |||
| {{cite journal |doi=10.2307/2323537 |title=Cross products of vectors in higher dimensional Euclidean spaces |author=WS Massey |journal=The American Mathematical Monthly |volume=90 |month=Dec. |year=1983 |pages=697–701 |url=http://www.jstor.org/stable/2323537 |issue=10 |publisher=Mathematical Association of America |ref=harv}} | |||
| </ref> | </ref> | ||
| :<math> \|\mathbf{a} \times \mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a} \cdot \mathbf{b})^2 </math> | |||
| which involves the ]. The right-hand side is called the ] of '''a''' and '''b''', and represents the square of the area of the parallelogram formed by these two vectors. From this requirement along with that of orthogonality of the cross product to its constituents '''a''' and '''b''', it follows that, apart from the trivial cases of zero and one dimensions, the cross product is defined only in three and seven dimensions.<ref name=n_dimensions> | |||
| :<math> \cosh \frac{c}{R} = \cosh \frac{a}{R} \, \cosh \frac{b}{R} </math> | |||
| Although a cross-product involving ''n''−1 vectors can be found in ''n''-dimensions, a cross-product involving only two vectors can be found only in 3-dimensions and in 7-dimensions. See {{cite book |title=Clifford algebras and spinors |author=Pertti Lounesto |url=http://books.google.com/?id=kOsybQWDK4oC&pg=PA96 |page=96 |chapter=§7.4 Cross product of two vectors |isbn=0521005515 |year=2001 |publisher=Cambridge University Press |edition=2nd}} | |||
| where cosh is the ]. This formula is a special form of the ] that applies to all hyperbolic triangles:<ref name=Gilman> | |||
| </ref> Using the definition of angle in ''n''-dimensions:<ref name=Hildebrand> | |||
| {{cite book |title=Two-generator discrete subgroups of PSL(2,R) |author=Jane Gilman|author-link=Jane Piore Gilman |chapter-url=https://books.google.com/books?id=YRFz9Zj_vAAC&pg=PA74 |chapter=Hyperbolic triangles |isbn=0-8218-0361-1 |year=1995 |publisher=American Mathematical Society Bookstore}} | |||
| {{cite book |title=Methods of applied mathematics |author=Francis Begnaud Hildebrand |page=24 |url=http://books.google.com/?id=17EZkWPz_eQC&pg=PA24|isbn=0486670023 |edition=Reprint of Prentice-Hall 1965 2nd|publisher=Courier Dover Publications |year=1992}} | |||
| </ref> | </ref> | ||
| :<math> (\mathbf{a \cdot b}) = ab \ \cos \theta \ , </math> | |||
| this property of the cross product provides its magnitude as: | |||
| :<math> |
:<math>\cosh \frac{c}{R} = \cosh \frac{a}{R} \ \cosh \frac{b}{R} - \sinh \frac{a}{R} \ \sinh \frac{b}{R} \ \cos \gamma \ , </math> | ||
| with γ the angle at the vertex opposite the side {{mvar|c}}. | |||
| Through the ],<ref name= Leff/> another form for the magnitude is found: | |||
| By using the ] for the hyperbolic cosine, {{math|cosh ''x'' ≈ 1 + ''x''<sup>2</sup>/2}}, it can be shown that as a hyperbolic triangle becomes very small (that is, as {{mvar|a}}, {{mvar|b}}, and {{mvar|c}} all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras' theorem. | |||
| :<math> \|\mathbf{ a \times b}\|= ab\ \sin \theta \, \ . </math> | |||
| For small right triangles {{math|(''a'', ''b'' << ''R'')}}, the hyperbolic cosines can be eliminated to avoid ], giving | |||
| An alternative approach defines the cross product using this expression for its magnitude. Then reversing the above argument, the connection to the dot product: | |||
| :<math> \sinh^2 \frac{c}{2R} = \sinh^2 \frac{a}{2R} + \sinh^2 \frac{b}{2R} + 2 \sinh^2 \frac{a}{2R} \sinh^2 \frac{b}{2R} \,.</math> | |||
| ====Very small triangles==== | |||
| :<math> \|\mathbf{a} \times \mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a} \cdot \mathbf{b})^2 ,</math> | |||
| For any uniform curvature {{mvar|K}} (positive, zero, or negative), in very small right triangles (|''K''|''a''<sup>2</sup>, |''K''|''b''<sup>2</sup> << 1) with hypotenuse {{mvar|c}}, it can be shown that | |||
| :<math> c^2 = a^2 + b^2 - \frac{K}{3} a^2 b^2 - \frac{K^2}{45} a^2 b^2 (a^2 + b^2) - \frac{2 K^3}{945} a^2 b^2 (a^2 - b^2)^2 + O (K^4 c^{10}) \,.</math> | |||
| ===Differential geometry=== | |||
| is derived. | |||
| ] (top) and ] (bottom), as given by Pythagoras' theorem]] | |||
| The Pythagorean theorem applies to ] triangles seen in ]. In three dimensional space, the distance between two infinitesimally separated points satisfies | |||
| ==History== | |||
| ] records Pythagorean triples from Babylonian times.<ref name=Neugebauer/>]] | |||
| ] (Compare with the top right ].)]] | |||
| There is debate whether the Pythagorean theorem was discovered once, or many times in many places. | |||
| :<math>ds^2 = dx^2 + dy^2 + dz^2,</math> | |||
| The history of the theorem can be divided into four parts: knowledge of ], knowledge of the relationship among the sides of a ], knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system. | |||
| with ''ds'' the element of distance and (''dx'', ''dy'', ''dz'') the components of the vector separating the two points. Such a space is called a ]. However, in ], a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:<ref name=Chow>{{cite book |title=Mathematical methods for physicists: a concise introduction |author=Tai L. Chow |page=52 |isbn=0-521-65544-7 |year=2000 |publisher=Cambridge University Press }}</ref> | |||
| ]s from circa 2500 BC in ], and in ], incorporate right triangles with integer sides.<ref>{{cite web|url=http://hyperion.cc.uregina.ca/~astro/Mega_circ.html|title=Megalithic Monuments.}}</ref> | |||
| ] conjectures that these Pythagorean triples were discovered ]ically by the Babylonians.<ref>{{harv|van_der_Waerden|1983|p=5}} | |||
| :<math>ds^2 = \sum_{i,j}^n g_{ij}\, dx_i\, dx_j </math> | |||
| See also {{cite book |title=Was Pythagoras Chinese?: An examination of right triangle theory in ancient China |author= Frank Swetz, T. I. Kao |url=http://books.google.com/?id=WaaGNz9G7l8C&pg=PA12&dq=%22Babylonian+tables+of+number+triples%22&cd=1#v=onepage&q=%22Babylonian%20tables%20of%20number%20triples%22 |isbn=0271012382 |year=1977 |publisher=Penn State Press | |||
| |page=12}} | |||
| </ref> | |||
| which is called the ]. (Sometimes, by abuse of language, the same term is applied to the set of coefficients {{math|''g''<sub>''ij''</sub>}}.) It may be a function of position, and often describes ]. A simple example is Euclidean (flat) space expressed in ]. For example, in ]: | |||
| Written between 2000 and 1786 BC, the ] ]ian papyrus '']'' includes a problem whose solution is a ]. | |||
| :<math>ds^2 = dr^2 + r^2 d\theta^2 \ . </math> | |||
| The ]n tablet '']'', written between ] and 1750 BC during the reign of ] the Great, contains many entries closely related to Pythagorean triples. | |||
| ==History== | |||
| In ], the ''] ]'', the dates of which are given variously as between the 8th century BC and the 2nd century BC, contains a list of ] discovered algebraically, a statement of the Pythagorean theorem, and a ] proof of the Pythagorean theorem for an ] right triangle. | |||
| ] records ] from ] times.<ref name=Neugebauer>{{harvnb|Neugebauer|1969|p=36}}.</ref>]] | |||
| The ''] Sulba Sutra'' (circa 600 BC) contains a numerical proof of the general Pythagorean theorem, using an area computation. ] believes that "it was certainly based on earlier traditions". According to Albert Bŭrk, this is the original proof of the theorem; he further theorizes that Pythagoras visited ], India, and copied it. Boyer (1991) thinks the elements found in the ] may be of Mesopotamian derivation.<ref> | |||
| There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of ] mathematics have concluded that the Pythagorean rule was in widespread use during the ] (20th to 16th centuries BC), over a thousand years before ] was born.<ref>{{harvnb|Neugebauer|1969}}: p. 36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."</ref><ref>{{cite journal|author=Friberg, Jöran|url=https://www.researchgate.net/publication/222892801|title=Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations|journal= Historia Mathematica|volume=8|pages=277–318|year=1981|doi=10.1016/0315-0860(81)90069-0|doi-access=free}}: p. 306 "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period."</ref><ref>{{cite conference | last=Høyrup | first=Jens | author-link=Jens Høyrup| contribution=Pythagorean ‘Rule’ and ‘Theorem’ – Mirror of the Relation Between Babylonian and Greek Mathematics | pages=393–407 | editor-last=Renger | editor-first=Johannes | title=Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin | publisher=Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag | url=http://akira.ruc.dk/~jensh/Publications/Pythrule.pdf}}, p. 406, "''To judge from this evidence alone'' it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db<sub>2</sub>-146, somewhere between 2300 and 1825 BC." (] is an Old Babylonian clay tablet from ] concerning the computation of the sides of a rectangle given its area and diagonal.)</ref><ref>{{cite book |author-link=Eleanor Robson |last=Robson |first=E. |title=Mathematics in Ancient Iraq: A Social History |publisher=Princeton University Press |year=2008 }}: p. 109 "Many Old Babylonian mathematical practitioners … knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste ‘algebra’ on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia."</ref> The history of the theorem can be divided into four parts: knowledge of ], knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some ]. | |||
| Written {{c.}} 1800{{nbsp}}BC, the ]ian ] '']'' includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. The Mesopotamian tablet '']'', written near ] also {{c.}} 1800{{nbsp}}BC, contains many entries closely related to Pythagorean triples.<ref>{{cite journal |last=Robson |first=Eleanor |authorlink=Eleanor Robson |year=2001 |title=Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322 |journal=Historia Mathematica |volume=28 |issue=3 |pages=167–206 |url=https://ora.ox.ac.uk/objects/uuid:e3d8eedb-e745-45b3-8612-71f8951599aa |doi=10.1006/hmat.2001.2317 |doi-access=free }}</ref> | |||
| {{cite book|author=Carl Benjamin Boyer|authorlink=Carl Benjamin Boyer|year=1968|title=A history of mathematics|url=http://books.google.com/?id=1ZDuAAAAMAAJ&cd=1&dq=China+and+India+rules+for+the+construction+of+right+angles+inauthor%3ACarl+inauthor%3ABenjamin+inauthor%3ABoyer&q=diagonal+of+a+rectangle+is+equal+to+the+sum+#search_anchor|chapter=China and India|page=229|quote=we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. However all of these triads are easily derived from the old Babylonian rule; hence, Mesopotamian influence in the ''Sulvasũtras'' is not unlikely. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides, but this form of the Pythagorean theorem also may have been derived from Mesopotamia. So conjectural are the origin and period of the ''Sulvasũtras'' that we cannot tell whether or not the rules are related to early Egyptian surveying or to the later Greek problem of altar doubling. They are variously dated within an interval of almost a thousand years stretching from the eighth century B.C. to the second century of our era.|publisher=Wiley}}; See also {{cite book |title=A History of Mathematics |author=Carl B. Boyer , Uta C. Merzbach |isbn=0470525487 |url=http://books.google.com/?id=xwIZQwAACAAJ&printsec=frontcover&dq=editions:UOM39015015720447 |publisher=Wiley |edition=3rd |year=2010}}</ref> | |||
| In ], the ''] ]'', the dates of which are given variously as between the 8th and 5th century BC,<ref>{{cite book|author=Kim Plofker |title=Mathematics in India|title-link= Mathematics in India (book)|pages= |year=2009|publisher=Princeton University Press |isbn=978-0-691-12067-6 }}</ref> contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the ] ] and in the general case, as does the ''] Shulba Sutra'' ({{circa|600 BC}}).{{efn|] believed that this material "was certainly based on earlier traditions".<ref>{{cite book|author=Bartel L. van der Waerden|title=Geometry and Algebra in Ancient Civilizations|publisher=Springer Science & Business Media|year=2012|page=26}}</ref> Carl Boyer states that the Pythagorean theorem in the '']'' may have been influenced by ancient Mesopotamian math, but there is no conclusive evidence in favor or opposition of this possibility.<ref>{{cite book|author1=Carl Benjamin Boyer |author-link=Carl Benjamin Boyer |author2=Uta C. Merzbach|author2-link=Uta Merzbach|year=2011 |title=A history of mathematics |edition=3rd |url=https://books.google.com/books?id=bR9HAAAAQBAJ |chapter=China and India| page=229| isbn= 978-0470525487 |quote='''Quote:''' we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the ''Sulvasũtras'' is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's ''Elements''. (...)|publisher=Wiley}}</ref>}} | |||
| With contents known much earlier, but in surviving texts dating from roughly the first century BC, the ] text '']'' (周髀算经), (''The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven'') gives an argument for the Pythagorean theorem for the (3, 4, 5) triangle—in China it is called the "Gougu Theorem" (勾股定理).<ref name=Crease> | |||
| ] ] philosopher and mathematician ], writing in the fifth century AD, states two arithmetic rules, "one of them attributed to ], the other to Pythagoras",<ref>{{cite book|author=Proclus|title= A Commentary of the First Book of Euclid's ''Elements''|at=428.6|translator-last=Morrow|translator-first=Glenn R.|publisher=Princeton University Press|year=1970}}</ref> for generating special Pythagorean triples. The rule attributed to Pythagoras ({{circa|570|495 BC}}) starts from an ] and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to ] (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived.<ref>{{Cite web|url=https://books.google.com/books?id=UhgPAAAAIAAJ&pg=PA351|title=Introduction and books 1,2|date=March 25, 1908|publisher=The University Press|via=Google Books}}</ref> However, when authors such as ] and ] attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.<ref name="heath144">{{harv|Heath|1921|loc=Vol I, p. 144}}: "Though this is the proposition universally associated by tradition with the name of Pythagoras, no really trustworthy evidence exists that it was actually discovered by him. The comparatively late writers who attribute it to him add the story that he sacrificed an ox to celebrate his discovery."</ref><ref name=Heath3> | |||
| {{cite book |title=The great equations: breakthroughs in science from Pythagoras to Heisenberg |page=25 |author=Robert P. Crease |isbn=039306204X |year=2008 |publisher=W W Norton & Co.}} | |||
| An extensive discussion of the historical evidence is provided in {{Harv|Euclid|1956|p=351}} </ref> ] ] wrote, "Whether this formula is rightly attributed to Pythagoras personally ... one can safely assume that it belongs to the very oldest period of ]."<ref name=Fritz/> Around 300 BC, in Euclid's ''Elements'', the oldest extant ] of the theorem is presented.<ref name="Aaboe"> | |||
| </ref><ref name=Cullen> | |||
| {{cite book|url=https://books.google.com/books?id=5wGzF0wPFYgC&pg=PA51|title=Episodes from the early history of mathematics|author=Asger Aaboe|publisher=Mathematical Association of America|year=1997|isbn=0-88385-613-1|page=51|quote=...it is not until Euclid that we find a logical sequence of general theorems with proper proofs.}}</ref> | |||
| ]'']] | |||
| A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by {{cite book |title=Astronomy and Mathematics in Ancient China: The 'Zhou Bi Suan Jing' |author=Christopher Cullen |url=http://books.google.com/?id=U9E88abLP10C&pg=PA139&dq=to+datable++events+%22relate+the+material%22&cd=1#v=onepage&q=to%20datable%20%20events%20%22relate%20the%20material%22 |pages=139 ''f'' |isbn=0521035376 |year=2007 |publisher=Cambridge University Press }} | |||
| With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the ] text '']'' (周髀算经), (''The Arithmetical Classic of the ] and the Circular Paths of Heaven'') gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the "'''Gougu theorem'''" (勾股定理).<ref name=Crease> | |||
| {{cite book |title=The great equations: breakthroughs in science from Pythagoras to Heisenberg |page= |author=Robert P. Crease |isbn=978-0-393-06204-5 |year=2008 |publisher=W W Norton & Co. |url=https://archive.org/details/greatequationsbr0000crea/page/25 }} | |||
| </ref><ref name=Cullen>A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by {{cite book |title=Astronomy and Mathematics in Ancient China: The 'Zhou Bi Suan Jing' |author=Christopher Cullen |pages=139 ''ff'' |isbn=978-0-521-03537-8 |year=2007 |publisher=Cambridge University Press }}</ref> During the ] (202 BC to 220 AD), Pythagorean triples appear in '']'',<ref name=Hui> | |||
| This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. {{cite book |title=Sherlock Holmes in Babylon: and other tales of mathematical history |author=Philip D. Straffin Jr. |chapter=Liu Hui and the first golden age of Chinese mathematics |editor1=Marlow Anderson |editor2=Victor J. Katz |editor3=Robin J. Wilson |chapter-url=https://books.google.com/books?id=BKRE5AjRM3AC&pg=PA69 |pages=69 ''ff'' |isbn=0-88385-546-1 |year=2004 |publisher=Mathematical Association of America}} See particularly §3: ''Nine chapters on the mathematical art'', pp. 71 ''ff''. | |||
| </ref> During the ], from 202 BC to 220 AD, Pythagorean triples appear in '']'',<ref name=Hui> | |||
| This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. {{cite book |title=Sherlock Holmes in Babylon: and other tales of mathematical history |author=Philip D Straffin, Jr. |chapter=Liu Hui and the first golden age of Chinese mathematics |editor=Marlow Anderson, Victor J. Katz, Robin J. Wilson |url=http://books.google.com/books?id=BKRE5AjRM3AC&pg=PA69 |pages=69 ''ff'' |isbn=0883855461 |year=2004 |publisher=Mathematical Association of America}} See particularly §3: ''Nine chapters on the mathematical art'', pps. 71 ''ff''. | |||
| </ref> together with a mention of right triangles.<ref name=Shen> | </ref> together with a mention of right triangles.<ref name=Shen> | ||
| {{cite book |title=The nine chapters on the mathematical art: companion and commentary | |
{{cite book |title=The nine chapters on the mathematical art: companion and commentary |author1=Kangshen Shen |author2=John N. Crossley |author3=Anthony Wah-Cheung Lun |page=488 |url=https://books.google.com/books?id=eiTJHRGTG6YC&pg=PA488 |isbn=0-19-853936-3 |year=1999 |publisher=Oxford University Press}} | ||
| </ref> Some believe the theorem arose first in ]<ref name=Centaurus> | </ref> Some believe the theorem arose first in ] in the 11th century BC,<ref name=Centaurus> | ||
| In particular, Li Jimin; see {{cite book |title=Centaurus, Volume 39 |url= |
In particular, Li Jimin; see {{cite book |title=Centaurus, Volume 39 |url=https://books.google.com/books?id=UJlFAAAAYAAJ&q=%22Shang+Gao+Theorem%22 |pages=193, 205 |year=1997 |publisher=Munksgaard|location=Copenhagen}} | ||
| </ref> |
</ref> where it is alternatively known as the "'''Shang Gao theorem'''" (商高定理),<ref name=CY_Chen> | ||
| {{cite book |title= Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts|url= |
{{cite book |title= Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts|chapter-url=https://books.google.com/books?id=2Wxj0SW9hBgC&pg=PA139 |page=142 |chapter=§3.3.4 Chén Zǐ's formula and the Chóng-Chã method; Figure 40 |isbn=962-209-385-X |year=1996 |publisher=Hong Kong University Press |author1= Chen, Cheng-Yih}} | ||
| </ref> named after the Duke of Zhou's |
</ref> named after the ] astronomer and mathematician, whose reasoning composed most of what was in the ''Zhoubi Suanjing''.<ref name=Wu> | ||
| {{cite book |title=Selected works of Wen-tsün Wu |author=Wen-tsün Wu |url= |
{{cite book |title=Selected works of Wen-tsün Wu |author=Wen-tsün Wu |chapter-url=https://books.google.com/books?id=xV4lECaKDzwC&pg=PA158 |page=158 |chapter=The Gougu theorem |isbn=978-981-279-107-8 |year=2008 |publisher=World Scientific}} | ||
| </ref>) | |||
| ], whose dates are commonly given as 569–475 BC, used algebraic methods to construct Pythagorean triples, according to ] commentary on ]. Proklos, however, wrote between 410 and 485 AD. According to ], no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived.<ref>{{Harv|Euclid|1956|p=351}} | |||
| </ref> However, when authors such as ] and ] attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted.<ref name="heath144"/><ref name=Heath3> | |||
| An extensive discussion of the historical evidence is provided in {{Harv|Euclid|1956|p=351}} | |||
| </ref> "Whether this formula is rightly attributed to Pythagoras personally, one can safely assume that it belongs to the very oldest period of Pythagorean mathematics."<ref name=Fritz/> | |||
| Around 400 BC, according to Proklos, ] gave a method for finding Pythagorean triples that combined algebra and geometry. Circa 300 BC, in ], the oldest extant ] of the theorem is presented.<ref name= Aaboe> | |||
| {{cite book |title=Episodes from the early history of mathematics |author=Asger Aaboe |url=http://books.google.com/books?id=5wGzF0wPFYgC&pg=PA51 |page=51 |quote=...it is not until Euclid that we find a logical sequence of general theorems with proper proofs. |isbn=0883856131 |year=1997 |publisher=Mathematical Association of America}} | |||
| </ref> | </ref> | ||
| {{clear}} | |||
| ==Pop references to the Pythagorean theorem== | |||
| The Pythagorean theorem has arisen in ] in a variety of ways. | |||
| * A verse of the ] in the ] musical ], "About binomial theorem I'm teeming with a lot o' news, With many cheerful facts about the square of the hypotenuse", with oblique reference to the theorem. | |||
| * The ] of '']'' makes a more specific reference to the theorem when he receives his diploma from the ]. He immediately exhibits his "knowledge" by reciting a mangled and incorrect version of the theorem: "The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side. Oh, joy! Oh, rapture! I've got a brain!" The "knowledge" exhibited by the Scarecrow is incorrect.<ref>{{cite web|url=http://www.imdb.com/title/tt0032138/quotes?qt0409923|title=The Scarecrow's Formula |work=Internet Movie Data Base |accessdate=2010-05-12}}</ref> | |||
| * In 2000, ] released a coin with the shape of an isosceles right triangle. The coin's tail has an image of Pythagoras and the equation α<sup>2</sup> + β<sup>2</sup> = γ<sup>2</sup>, accompanied with the mention "Pythagoras Millennium".<ref>{{cite web|url=http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm|title=Le Saviez-vous ?}}</ref> ], ], ], ], and ] have issued ] depicting Pythagoras and the Pythagorean theorem.<ref>{{cite web|url=http://jeff560.tripod.com/stamps.html|title=Images of Mathematicians on Postage Stamps|first=Jeff|last=Miller|date=2007-08-03|accessdate=2010-07-18}}</ref> | |||
| * In ]'s speculative fiction '']'', the Pythagorean theorem is referred to as 'the Adrakhonic theorem'. A geometric proof of the theorem is displayed on the side of an alien ship to demonstrate their understanding of mathematics. | |||
| ==See also== | ==See also== | ||
| {{Portal|Mathematics}} | |||
| <div style="-moz-column-count:2; column-count:2"> | |||
| {{Div col}} | |||
| *] | |||
| *{{annotated link|At Dulcarnon}} | |||
| *] | *] | ||
| *{{annotated link|Bride's Chair}} | |||
| *] | |||
| *] | *] | ||
| *] | |||
| *{{annotated link|Hsuan thu}} | |||
| *] | |||
| *] | |||
| *] | *] | ||
| *] | *] | ||
| *] | *] | ||
| *] | *] | ||
| *] | *] | ||
| *{{annotated link|Parseval's identity}} | |||
| *] | |||
| *{{annotated link|Ptolemy's theorem}} | |||
| *] | |||
| *] | *] | ||
| *] | *] | ||
| *] | |||
| *] | |||
| * |
*{{annotated link|Thales theorem}} | ||
| {{Div col end}} | |||
| *] | |||
| </div> | |||
| ==Notes== | ==Notes and references== | ||
| ===Notes=== | |||
| {{reflist|colwidth=30em}} | |||
| {{Notelist}} | |||
| ==References== | ===References=== | ||
| {{Reflist}} | |||
| ===Works cited=== | |||
| * {{Cite book |last=Bell |first=John L. |url=http://publish.uwo.ca/~jbell/ |title=The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development |publisher=Kluwer |year=1999 |isbn=0-7923-5972-0|ref=harv |postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->}} | |||
| {{Refbegin}} | |||
| * {{Cite book |last=Euclid |title= The Elements (3 vols.) |editor=Translated by Johan Ludvig Heiberg with an introduction and commentary by Sir Thomas L. Heath|publisher=Dover |edition=Reprint of 1908 |year= 1956 |volume= Vol. 1 (Books I and II)|isbn= 0-486-60088-2|ref=harv |postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->}} On-line text at | |||
| * {{Cite book |last=Bell |first=John L. |url=http://publish.uwo.ca/~jbell/ |title=The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development |publisher=Kluwer |year=1999 |isbn=0-7923-5972-0 }} | |||
| *{{cite book |title=A History of Greek Mathematics (2 Vols.)|last=Heath |first=Sir Thomas |publisher= Clarendon Press, Oxford |url=http://books.google.com/?id=h4JsAAAAMAAJ&pg=PA144 |page=144 ''ff'' |chapter=The 'Theorem of Pythagoras' |year=1921 |edition= Dover Publications, Inc. (1981) |isbn= 0-486-24073-8|ref=harv}} | |||
| * {{Cite book |last=Euclid |title= The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary |translator-last=Heath | translator-first=Thomas L. |publisher=Dover |edition=Reprint of 2nd (1925) |year= 1956 |volume= 1 (Books I and II)}} On-line text at | |||
| <!-- * {{Cite book |last= Kaplan|first=Robert and Ellen| title=Hidden Harmonies: The Lives and Times of the Pythagorean Theorem |location=New York, NY |publisher=Bloomsbury Press |url=http://www.bloomsburypress.com/books/catalog/hidden_harmonies_hc_220 |year=2011 |isbn=9781596915220|ref=harv }} --> | |||
| *{{cite book |title= |
*{{cite book |title=A History of Greek Mathematics (2 Vols.)|last=Heath |first=Sir Thomas |publisher= Clarendon Press, Oxford |chapter-url=https://books.google.com/books?id=h4JsAAAAMAAJ&pg=PA144 |pages=144 ''ff'' |chapter=The 'Theorem of Pythagoras' |year=1921 |edition= Dover Publications, Inc. (1981) |isbn= 0-486-24073-8}} | ||
| <!-- * {{Cite book |last= Kaplan|first=Robert and Ellen| title=Hidden Harmonies: The Lives and Times of the Pythagorean Theorem |location=New York, NY |publisher=Bloomsbury Press |url=http://www.bloomsburypress.com/books/catalog/hidden_harmonies_hc_220 |year=2011 |isbn=978-1-59691-522-0 }} --> | |||
| * {{Cite book |last=Loomis |first=Elisha Scott |title=The Pythagorean proposition|edition= 2nd |publisher= The National Council of Teachers of Mathematics |year=1968 |isbn=978-0873530361|ref=harv |postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->}} For full text of 2nd edition of 1940, see {{cite web|url=http://www.eric.ed.gov/PDFS/ED037335.pdf|author=Elisha Scott Loomis |title=The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs |accessdate=2010-05-04 |work=] |publisher=] (IES) of the ] }}{{dead link|date=July 2010}} Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, isbn=0873530365. | |||
| * |
*{{cite book |title=Euclidean and transformational geometry: a deductive inquiry |last=Libeskind |first=Shlomo |url=https://books.google.com/books?id=6YUUeO-RjU0C&pg=PA41 |isbn=978-0-7637-4366-6 |year=2008 |publisher=Jones & Bartlett Learning }} This high-school geometry text covers many of the topics in this WP article. | ||
| * {{Cite book |last=Loomis |first=Elisha Scott |title=The Pythagorean Proposition |edition=2nd |year=1940 |publisher=Edwards Brothers |isbn=9780873530361 |place=Ann Arbor, Michigan |url=https://archive.org/details/pythagoreanpropo0000loom_b2m3/ |url-access=limited }} Reissued 1968 by the National Council of Teachers of Mathematics. A lower-quality scan was published online by the ], . | |||
| * {{Cite book |last=Stillwell |first=John |title=Mathematics and Its History |publisher= Springer-Verlag |year=1989 |isbn=0-387-96981-0|ref=harv |postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->}} Also ISBN 3-540-96981-0. | |||
| *{{Cite book |last= |
* {{Cite book |last= Maor |first=Eli |title=The Pythagorean Theorem: A 4,000-Year History |location=Princeton, New Jersey |publisher=Princeton University Press |url=https://books.google.com/books?id=Z5VoBGy3AoAC |year=2007 |isbn=978-0-691-12526-8}} | ||
| * {{cite book |title=The exact sciences in antiquity |url=https://books.google.com/books?id=JVhTtVA2zr8C&pg=PA36 |last=Neugebauer|first= Otto | isbn=0-486-22332-9 |oclc=638685764 |year=1969 |edition= 2nd |publisher=Courier Dover Publications}} | |||
| *{{Cite book |last=van der Waerden |first=Bartel Leendert |title=Geometry and Algebra in Ancient Civilizations |publisher=Springer |year=1983 |isbn=3540121595 |url=http://books.google.com/?id=_vPuAAAAMAAJ&q=%22Pythagorean+triples%22++%22Babylonian+scribes%22+inauthor:van+inauthor:der+inauthor:Waerden&dq=%22Pythagorean+triples%22++%22Babylonian+scribes%22+inauthor:van+inauthor:der+inauthor:Waerden&cd=1 |ref=harv |postscript=<!-- Bot inserted parameter. Either remove it; or change its value to "." for the cite to end in a ".", as necessary. -->}} | |||
| * Robson, Eleanor and Jacqueline Stedall, eds., The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, 2009. pp. vii + 918. {{ISBN|978-0-19-921312-2}}. | |||
| </div> | |||
| * {{Cite book |last=Stillwell |first=John |title=Mathematics and Its History |publisher=Springer-Verlag |year=1989 |isbn=0-387-96981-0 |url-access=registration |url=https://archive.org/details/mathematicsitshi0000stil }} Also {{isbn|3-540-96981-0}}. | |||
| *{{Cite book |last1=Swetz |first1=Frank |author2=Kao, T. I. |title=Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China |publisher=Pennsylvania State University Press |year=1977 |isbn=0-271-01238-2 |url-access=registration |url=https://archive.org/details/waspythagoraschi0000swet }} | |||
| *{{Cite book |last=van der Waerden |first=Bartel Leendert |title=Geometry and Algebra in Ancient Civilizations |publisher=Springer |year=1983 |isbn=3-540-12159-5 |url=https://archive.org/details/geometryalgebrai0000waer |url-access=registration |quote=Pythagorean triples Babylonian scribes van der Waerden. }} | |||
| {{Refend}} | |||
| ==External links== | ==External links== | ||
| {{Commons category}} | {{Commons category}} | ||
| * (more than 70 proofs from ]) | |||
| * Interactive links: | |||
| ** in ] of The Pythagorean Theorem | |||
| ** in ] of The Pythagorean Theorem | |||
| ** with interactive animation | |||
| ** Pythagorean Theorem | |||
| * | |||
| * | |||
| * {{MathWorld|title=Pythagorean theorem|urlname=PythagoreanTheorem}} | |||
| {{commons category|Elements of Euclid}} | |||
| *{{cite book | *{{cite book | ||
| | |
| author = Euclid | ||
| | editor = David E. Joyce | |||
| | title = Elements | | title = Elements | ||
| | |
| orig-year = c. 300 BC | ||
| | url = http://aleph0.clarku.edu/~djoyce/java/elements/toc.html | | url = http://aleph0.clarku.edu/~djoyce/java/elements/toc.html | ||
| | |
| access-date = 2006-08-30 | ||
| | year = |
| year = 1997 | ||
| }} In HTML with Java-based interactive figures. | }} In HTML with Java-based interactive figures. | ||
| * {{springer|title=Pythagorean theorem|id=p/p075940|mode=cs1}} | |||
| * | |||
| * Interactive links: | |||
| ** in ] of the Pythagorean theorem | |||
| ** in ] of the Pythagorean theorem | |||
| ** with interactive animation | |||
| ** Pythagorean theorem | |||
| * on YouTube | |||
| * (more than 70 proofs from ]) | |||
| * {{MathWorld|title=Pythagorean theorem|urlname=PythagoreanTheorem}} | |||
| {{ |
{{Authority control}} | ||
| {{Good article}} | |||
| {{DEFAULTSORT:Pythagorean |
{{DEFAULTSORT:Pythagorean theorem}} | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | |||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
| {{Link GA|ar}} | |||
| {{Link GA|eo}} | |||
| {{Link FA|bar}} | |||
| {{Link FA|de}} | |||
| {{Link FA|fr}} | |||
| {{Link FA|he}} | |||
| {{Link FA|sr}} | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
| ] | |||
Latest revision as of 02:48, 6 January 2025
Relation between sides of a right triangle
 | |
| Type | Theorem |
|---|---|
| Field | Euclidean geometry |
| Statement | The sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse (c). |
| Symbolic statement | |
| Generalizations | |
| Consequences | |
| Geometry | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 Projecting a sphere to a plane Projecting a sphere to a plane | ||||||||||
| Branches | ||||||||||
|
||||||||||
| Zero-dimensional | ||||||||||
| One-dimensional | ||||||||||
Two-dimensional
|
||||||||||
| Three-dimensional | ||||||||||
| Four- / other-dimensional | ||||||||||
| Geometers | ||||||||||
by name
|
||||||||||
by period
|
||||||||||
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides.
The theorem can be written as an equation relating the lengths of the sides a, b and the hypotenuse c, sometimes called the Pythagorean equation:
The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proved numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years.
When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared distance between two points equals the sum of squares of the difference in each coordinate between the points.
The theorem can be generalized in various ways: to higher-dimensional spaces, to spaces that are not Euclidean, to objects that are not right triangles, and to objects that are not triangles at all but n-dimensional solids.
Proofs using constructed squares
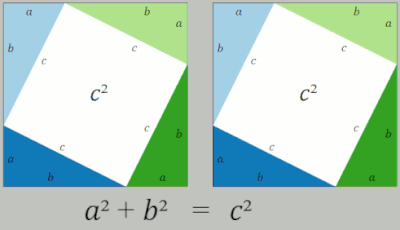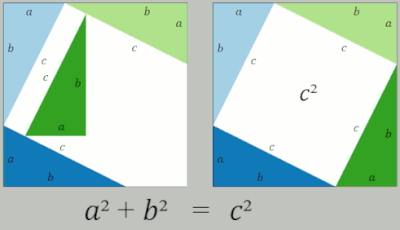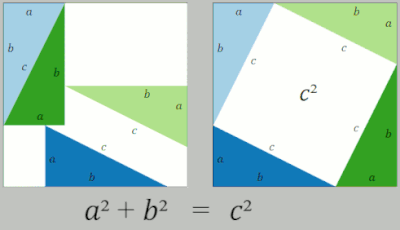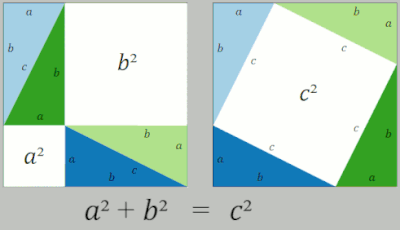
(The area of the white space remains constant throughout the translation rearrangement of the triangles. At all moments in time, the area is always c. And likewise, at all moments in time, the area is always a + b.)
Rearrangement proofs
In one rearrangement proof, two squares are used whose sides have a measure of and which contain four right triangles whose sides are a, b and c, with the hypotenuse being c. In the square on the right side, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length c. Each outer square has an area of as well as , with representing the total area of the four triangles. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length a and b. These rectangles in their new position have now delineated two new squares, one having side length a is formed in the bottom-left corner, and another square of side length b formed in the top-right corner. In this new position, this left side now has a square of area as well as . Since both squares have the area of it follows that the other measure of the square area also equal each other such that = . With the area of the four triangles removed from both side of the equation what remains is
In another proof rectangles in the second box can also be placed such that both have one corner that correspond to consecutive corners of the square. In this way they also form two boxes, this time in consecutive corners, with areas and which will again lead to a second square of with the area .
English mathematician Sir Thomas Heath gives this proof in his commentary on Proposition I.47 in Euclid's Elements, and mentions the proposals of German mathematicians Carl Anton Bretschneider and Hermann Hankel that Pythagoras may have known this proof. Heath himself favors a different proposal for a Pythagorean proof, but acknowledges from the outset of his discussion "that the Greek literature which we possess belonging to the first five centuries after Pythagoras contains no statement specifying this or any other particular great geometric discovery to him." Recent scholarship has cast increasing doubt on any sort of role for Pythagoras as a creator of mathematics, although debate about this continues.
Algebraic proofs
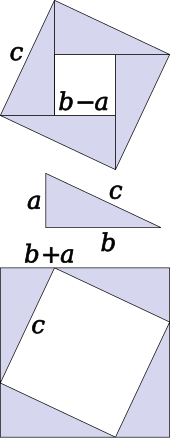
The theorem can be proved algebraically using four copies of the same triangle arranged symmetrically around a square with side c, as shown in the lower part of the diagram. This results in a larger square, with side a + b and area (a + b). The four triangles and the square side c must have the same area as the larger square,
giving
A similar proof uses four copies of a right triangle with sides a, b and c, arranged inside a square with side c as in the top half of the diagram. The triangles are similar with area , while the small square has side b − a and area (b − a). The area of the large square is therefore
But this is a square with side c and area c, so
Other proofs of the theorem
This theorem may have more known proofs than any other (the law of quadratic reciprocity being another contender for that distinction); the book The Pythagorean Proposition contains 370 proofs.
Proof using similar triangles
In this section, and as usual in geometry, a "word" of two capital letters, such as AB denotes the length of the line segment defined by the points labeled with the letters, and not a multiplication. So, AB denotes the square of the length AB and not the product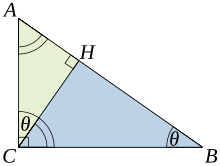
This proof is based on the proportionality of the sides of three similar triangles, that is, upon the fact that the ratio of any two corresponding sides of similar triangles is the same regardless of the size of the triangles.
Let ABC represent a right triangle, with the right angle located at C, as shown on the figure. Draw the altitude from point C, and call H its intersection with the side AB. Point H divides the length of the hypotenuse c into parts d and e. The new triangle, ACH, is similar to triangle ABC, because they both have a right angle (by definition of the altitude), and they share the angle at A, meaning that the third angle will be the same in both triangles as well, marked as θ in the figure. By a similar reasoning, the triangle CBH is also similar to ABC. The proof of similarity of the triangles requires the triangle postulate: The sum of the angles in a triangle is two right angles, and is equivalent to the parallel postulate. Similarity of the triangles leads to the equality of ratios of corresponding sides:
The first result equates the cosines of the angles θ, whereas the second result equates their sines.
These ratios can be written as
Summing these two equalities results in
which, after simplification, demonstrates the Pythagorean theorem:
The role of this proof in history is the subject of much speculation. The underlying question is why Euclid did not use this proof, but invented another. One conjecture is that the proof by similar triangles involved a theory of proportions, a topic not discussed until later in the Elements, and that the theory of proportions needed further development at that time.
Einstein's proof by dissection without rearrangement
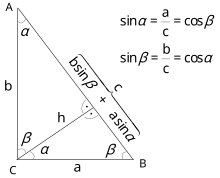
Albert Einstein gave a proof by dissection in which the pieces do not need to be moved. Instead of using a square on the hypotenuse and two squares on the legs, one can use any other shape that includes the hypotenuse, and two similar shapes that each include one of two legs instead of the hypotenuse (see Similar figures on the three sides). In Einstein's proof, the shape that includes the hypotenuse is the right triangle itself. The dissection consists of dropping a perpendicular from the vertex of the right angle of the triangle to the hypotenuse, thus splitting the whole triangle into two parts. Those two parts have the same shape as the original right triangle, and have the legs of the original triangle as their hypotenuses, and the sum of their areas is that of the original triangle. Because the ratio of the area of a right triangle to the square of its hypotenuse is the same for similar triangles, the relationship between the areas of the three triangles holds for the squares of the sides of the large triangle as well.
Euclid's proof

In outline, here is how the proof in Euclid's Elements proceeds. The large square is divided into a left and right rectangle. A triangle is constructed that has half the area of the left rectangle. Then another triangle is constructed that has half the area of the square on the left-most side. These two triangles are shown to be congruent, proving this square has the same area as the left rectangle. This argument is followed by a similar version for the right rectangle and the remaining square. Putting the two rectangles together to reform the square on the hypotenuse, its area is the same as the sum of the area of the other two squares. The details follow.
Let A, B, C be the vertices of a right triangle, with a right angle at A. Drop a perpendicular from A to the side opposite the hypotenuse in the square on the hypotenuse. That line divides the square on the hypotenuse into two rectangles, each having the same area as one of the two squares on the legs.
For the formal proof, we require four elementary lemmata:
- If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent (side-angle-side).
- The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
- The area of a rectangle is equal to the product of two adjacent sides.
- The area of a square is equal to the product of two of its sides (follows from 3).
Next, each top square is related to a triangle congruent with another triangle related in turn to one of two rectangles making up the lower square.
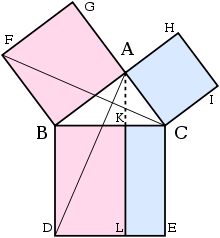
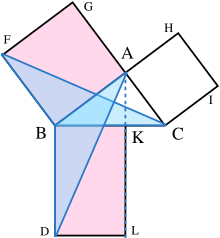
The proof is as follows:
- Let ACB be a right-angled triangle with right angle CAB.
- On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order. The construction of squares requires the immediately preceding theorems in Euclid, and depends upon the parallel postulate.
- From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
- Join CF and AD, to form the triangles BCF and BDA.
- Angles CAB and BAG are both right angles; therefore C, A, and G are collinear.
- Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
- Since AB is equal to FB, BD is equal to BC and angle ABD equals angle FBC, triangle ABD must be congruent to triangle FBC.
- Since A-K-L is a straight line, parallel to BD, then rectangle BDLK has twice the area of triangle ABD because they share the base BD and have the same altitude BK, i.e., a line normal to their common base, connecting the parallel lines BD and AL. (lemma 2)
- Since C is collinear with A and G, and this line is parallel to FB, then square BAGF must be twice in area to triangle FBC.
- Therefore, rectangle BDLK must have the same area as square BAGF = AB.
- By applying steps 3 to 10 to the other side of the figure, it can be similarly shown that rectangle CKLE must have the same area as square ACIH = AC.
- Adding these two results, AB + AC = BD × BK + KL × KC
- Since BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
- Therefore, AB + AC = BC, since CBDE is a square.
This proof, which appears in Euclid's Elements as that of Proposition 47 in Book 1, demonstrates that the area of the square on the hypotenuse is the sum of the areas of the other two squares. This is quite distinct from the proof by similarity of triangles, which is conjectured to be the proof that Pythagoras used.
Proofs by dissection and rearrangement
Another by rearrangement is given by the middle animation. A large square is formed with area c, from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a and b, which must have the same area as the initial large square.
The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse – or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.
 |
 |
 |
Proof by area-preserving shearing

As shown in the accompanying animation, area-preserving shear mappings and translations can transform the squares on the sides adjacent to the right-angle onto the square on the hypotenuse, together covering it exactly. Each shear leaves the base and height unchanged, thus leaving the area unchanged too. The translations also leave the area unchanged, as they do not alter the shapes at all. Each square is first sheared into a parallelogram, and then into a rectangle which can be translated onto one section of the square on the hypotenuse.
Other algebraic proofs
A related proof was published by future U.S. President James A. Garfield (then a U.S. Representative). Instead of a square it uses a trapezoid, which can be constructed from the square in the second of the above proofs by bisecting along a diagonal of the inner square, to give the trapezoid as shown in the diagram. The area of the trapezoid can be calculated to be half the area of the square, that is
The inner square is similarly halved, and there are only two triangles so the proof proceeds as above except for a factor of , which is removed by multiplying by two to give the result.
Proof using differentials
One can arrive at the Pythagorean theorem by studying how changes in a side produce a change in the hypotenuse and employing calculus.
The triangle ABC is a right triangle, as shown in the upper part of the diagram, with BC the hypotenuse. At the same time the triangle lengths are measured as shown, with the hypotenuse of length y, the side AC of length x and the side AB of length a, as seen in the lower diagram part.
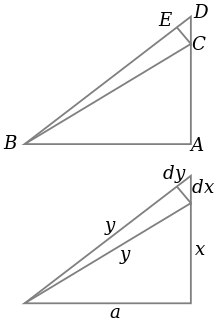
If x is increased by a small amount dx by extending the side AC slightly to D, then y also increases by dy. These form two sides of a triangle, CDE, which (with E chosen so CE is perpendicular to the hypotenuse) is a right triangle approximately similar to ABC. Therefore, the ratios of their sides must be the same, that is:
This can be rewritten as , which is a differential equation that can be solved by direct integration:
giving
The constant can be deduced from x = 0, y = a to give the equation
This is more of an intuitive proof than a formal one: it can be made more rigorous if proper limits are used in place of dx and dy.
Converse
The converse of the theorem is also true:
Given a triangle with sides of length a, b, and c, if a + b = c, then the angle between sides a and b is a right angle.
For any three positive real numbers a, b, and c such that a + b = c, there exists a triangle with sides a, b and c as a consequence of the converse of the triangle inequality.
This converse appears in Euclid's Elements (Book I, Proposition 48): "If in a triangle the square on one of the sides equals the sum of the squares on the remaining two sides of the triangle, then the angle contained by the remaining two sides of the triangle is right."
It can be proved using the law of cosines or as follows:
Let ABC be a triangle with side lengths a, b, and c, with a + b = c. Construct a second triangle with sides of length a and b containing a right angle. By the Pythagorean theorem, it follows that the hypotenuse of this triangle has length c = √a + b, the same as the hypotenuse of the first triangle. Since both triangles' sides are the same lengths a, b and c, the triangles are congruent and must have the same angles. Therefore, the angle between the side of lengths a and b in the original triangle is a right angle.
The above proof of the converse makes use of the Pythagorean theorem itself. The converse can also be proved without assuming the Pythagorean theorem.
A corollary of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute, as follows. Let c be chosen to be the longest of the three sides and a + b > c (otherwise there is no triangle according to the triangle inequality). The following statements apply:
- If a + b = c, then the triangle is right.
- If a + b > c, then the triangle is acute.
- If a + b < c, then the triangle is obtuse.
Edsger W. Dijkstra has stated this proposition about acute, right, and obtuse triangles in this language:
- sgn(α + β − γ) = sgn(a + b − c),
where α is the angle opposite to side a, β is the angle opposite to side b, γ is the angle opposite to side c, and sgn is the sign function.
Consequences and uses of the theorem
Pythagorean triples
Main article: Pythagorean triple See also: Formulas for generating Pythagorean triplesA Pythagorean triple has three positive integers a, b, and c, such that a + b = c. In other words, a Pythagorean triple represents the lengths of the sides of a right triangle where all three sides have integer lengths. Such a triple is commonly written (a, b, c). Some well-known examples are (3, 4, 5) and (5, 12, 13).
A primitive Pythagorean triple is one in which a, b and c are coprime (the greatest common divisor of a, b and c is 1).
The following is a list of primitive Pythagorean triples with values less than 100:
- (3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
There are many formulas for generating Pythagorean triples. Of these, Euclid's formula is the most well-known: given arbitrary positive integers m and n, the formula states that the integers
forms a Pythagorean triple.
Inverse Pythagorean theorem
Given a right triangle with sides and altitude (a line from the right angle and perpendicular to the hypotenuse ). The Pythagorean theorem has,
while the inverse Pythagorean theorem relates the two legs to the altitude ,
The equation can be transformed to,
where for any non-zero real . If the are to be integers, the smallest solution is then
using the smallest Pythagorean triple . The reciprocal Pythagorean theorem is a special case of the optic equation
where the denominators are squares and also for a heptagonal triangle whose sides are square numbers.
Incommensurable lengths

One of the consequences of the Pythagorean theorem is that line segments whose lengths are incommensurable (so the ratio of which is not a rational number) can be constructed using a straightedge and compass. Pythagoras' theorem enables construction of incommensurable lengths because the hypotenuse of a triangle is related to the sides by the square root operation.
The figure on the right shows how to construct line segments whose lengths are in the ratio of the square root of any positive integer. Each triangle has a side (labeled "1") that is the chosen unit for measurement. In each right triangle, Pythagoras' theorem establishes the length of the hypotenuse in terms of this unit. If a hypotenuse is related to the unit by the square root of a positive integer that is not a perfect square, it is a realization of a length incommensurable with the unit, such as √2, √3, √5 . For more detail, see Quadratic irrational.
Incommensurable lengths conflicted with the Pythagorean school's concept of numbers as only whole numbers. The Pythagorean school dealt with proportions by comparison of integer multiples of a common subunit. According to one legend, Hippasus of Metapontum (ca. 470 B.C.) was drowned at sea for making known the existence of the irrational or incommensurable. A careful discussion of Hippasus's contributions is found in Fritz.
Complex numbers

For any complex number
the absolute value or modulus is given by
So the three quantities, r, x and y are related by the Pythagorean equation,
Note that r is defined to be a positive number or zero but x and y can be negative as well as positive. Geometrically r is the distance of the z from zero or the origin O in the complex plane.
This can be generalised to find the distance between two points, z1 and z2 say. The required distance is given by
so again they are related by a version of the Pythagorean equation,
Euclidean distance
Main article: Euclidean distanceThe distance formula in Cartesian coordinates is derived from the Pythagorean theorem. If (x1, y1) and (x2, y2) are points in the plane, then the distance between them, also called the Euclidean distance, is given by
More generally, in Euclidean n-space, the Euclidean distance between two points, and , is defined, by generalization of the Pythagorean theorem, as:
If instead of Euclidean distance, the square of this value (the squared Euclidean distance, or SED) is used, the resulting equation avoids square roots and is simply a sum of the SED of the coordinates:
The squared form is a smooth, convex function of both points, and is widely used in optimization theory and statistics, forming the basis of least squares.
Euclidean distance in other coordinate systems
If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras' theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates (r, θ) can be introduced as:
Then two points with locations (r1, θ1) and (r2, θ2) are separated by a distance s:
Performing the squares and combining terms, the Pythagorean formula for distance in Cartesian coordinates produces the separation in polar coordinates as:
using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem. From this result, for the case where the radii to the two locations are at right angles, the enclosed angle Δθ = π/2, and the form corresponding to Pythagoras' theorem is regained: The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.
Pythagorean trigonometric identity
Main article: Pythagorean trigonometric identity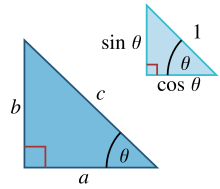
In a right triangle with sides a, b and hypotenuse c, trigonometry determines the sine and cosine of the angle θ between side a and the hypotenuse as:
From that it follows:
where the last step applies Pythagoras' theorem. This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity. In similar triangles, the ratios of the sides are the same regardless of the size of the triangles, and depend upon the angles. Consequently, in the figure, the triangle with hypotenuse of unit size has opposite side of size sin θ and adjacent side of size cos θ in units of the hypotenuse.
Relation to the cross product

The Pythagorean theorem relates the cross product and dot product in a similar way:
This can be seen from the definitions of the cross product and dot product, as
with n a unit vector normal to both a and b. The relationship follows from these definitions and the Pythagorean trigonometric identity.
This can also be used to define the cross product. By rearranging the following equation is obtained
This can be considered as a condition on the cross product and so part of its definition, for example in seven dimensions.
As an axiom
Main article: Parallel postulateIf the first four of the Euclidean geometry axioms are assumed to be true then the Pythagorean theorem is equivalent to the fifth. That is, Euclid's fifth postulate implies the Pythagorean theorem and vice-versa.
Generalizations
Similar figures on the three sides
The Pythagorean theorem generalizes beyond the areas of squares on the three sides to any similar figures. This was known by Hippocrates of Chios in the 5th century BC, and was included by Euclid in his Elements:
If one erects similar figures (see Euclidean geometry) with corresponding sides on the sides of a right triangle, then the sum of the areas of the ones on the two smaller sides equals the area of the one on the larger side.
This extension assumes that the sides of the original triangle are the corresponding sides of the three congruent figures (so the common ratios of sides between the similar figures are a:b:c). While Euclid's proof only applied to convex polygons, the theorem also applies to concave polygons and even to similar figures that have curved boundaries (but still with part of a figure's boundary being the side of the original triangle).
The basic idea behind this generalization is that the area of a plane figure is proportional to the square of any linear dimension, and in particular is proportional to the square of the length of any side. Thus, if similar figures with areas A, B and C are erected on sides with corresponding lengths a, b and c then:
But, by the Pythagorean theorem, a + b = c, so A + B = C.
Conversely, if we can prove that A + B = C for three similar figures without using the Pythagorean theorem, then we can work backwards to construct a proof of the theorem. For example, the starting center triangle can be replicated and used as a triangle C on its hypotenuse, and two similar right triangles (A and B ) constructed on the other two sides, formed by dividing the central triangle by its altitude. The sum of the areas of the two smaller triangles therefore is that of the third, thus A + B = C and reversing the above logic leads to the Pythagorean theorem a + b = c. (See also Einstein's proof by dissection without rearrangement)
 green area A + B = blue area C |
 |
 |
Law of cosines
Main article: Law of cosines
The Pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that where is the angle between sides and .
When is radians or 90°, then , and the formula reduces to the usual Pythagorean theorem.
Arbitrary triangle

At any selected angle of a general triangle of sides a, b, c, inscribe an isosceles triangle such that the equal angles at its base θ are the same as the selected angle. Suppose the selected angle θ is opposite the side labeled c. Inscribing the isosceles triangle forms triangle CAD with angle θ opposite side b and with side r along c. A second triangle is formed with angle θ opposite side a and a side with length s along c, as shown in the figure. Thābit ibn Qurra stated that the sides of the three triangles were related as:
As the angle θ approaches π/2, the base of the isosceles triangle narrows, and lengths r and s overlap less and less. When θ = π/2, ADB becomes a right triangle, r + s = c, and the original Pythagorean theorem is regained.
One proof observes that triangle ABC has the same angles as triangle CAD, but in opposite order. (The two triangles share the angle at vertex A, both contain the angle θ, and so also have the same third angle by the triangle postulate.) Consequently, ABC is similar to the reflection of CAD, the triangle DAC in the lower panel. Taking the ratio of sides opposite and adjacent to θ,
Likewise, for the reflection of the other triangle,
Clearing fractions and adding these two relations:
the required result.
The theorem remains valid if the angle is obtuse so the lengths r and s are non-overlapping.
General triangles using parallelograms
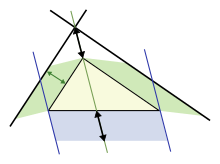
green area = blue area

Pappus's area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares (squares are a special case, of course). The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated (the dimensions labeled with arrows are the same, and determine the sides of the bottom parallelogram). This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras' theorem, and was considered a generalization by Pappus of Alexandria in 4 AD
The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base (the upper left side of the triangle) and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.
Solid geometry


In terms of solid geometry, Pythagoras' theorem can be applied to three dimensions as follows. Consider the cuboid shown in the figure. The length of face diagonal AC is found from Pythagoras' theorem as:
where these three sides form a right triangle. Using diagonal AC and the horizontal edge CD, the length of body diagonal AD then is found by a second application of Pythagoras' theorem as:
or, doing it all in one step:
This result is the three-dimensional expression for the magnitude of a vector v (the diagonal AD) in terms of its orthogonal components {vk} (the three mutually perpendicular sides):
This one-step formulation may be viewed as a generalization of Pythagoras' theorem to higher dimensions. However, this result is really just the repeated application of the original Pythagoras' theorem to a succession of right triangles in a sequence of orthogonal planes.
A substantial generalization of the Pythagorean theorem to three dimensions is de Gua's theorem, named for Jean Paul de Gua de Malves: If a tetrahedron has a right angle corner (like a corner of a cube), then the square of the area of the face opposite the right angle corner is the sum of the squares of the areas of the other three faces. This result can be generalized as in the "n-dimensional Pythagorean theorem":
Let be orthogonal vectors in R. Consider the n-dimensional simplex S with vertices . (Think of the (n − 1)-dimensional simplex with vertices not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.
This statement is illustrated in three dimensions by the tetrahedron in the figure. The "hypotenuse" is the base of the tetrahedron at the back of the figure, and the "legs" are the three sides emanating from the vertex in the foreground. As the depth of the base from the vertex increases, the area of the "legs" increases, while that of the base is fixed. The theorem suggests that when this depth is at the value creating a right vertex, the generalization of Pythagoras' theorem applies. In a different wording:
Given an n-rectangular n-dimensional simplex, the square of the (n − 1)-content of the facet opposing the right vertex will equal the sum of the squares of the (n − 1)-contents of the remaining facets.
Inner product spaces
The Pythagorean theorem can be generalized to inner product spaces, which are generalizations of the familiar 2-dimensional and 3-dimensional Euclidean spaces. For example, a function may be considered as a vector with infinitely many components in an inner product space, as in functional analysis.
In an inner product space, the concept of perpendicularity is replaced by the concept of orthogonality: two vectors v and w are orthogonal if their inner product is zero. The inner product is a generalization of the dot product of vectors. The dot product is called the standard inner product or the Euclidean inner product. However, other inner products are possible.
The concept of length is replaced by the concept of the norm ‖v‖ of a vector v, defined as:
In an inner-product space, the Pythagorean theorem states that for any two orthogonal vectors v and w we have
Here the vectors v and w are akin to the sides of a right triangle with hypotenuse given by the vector sum v + w. This form of the Pythagorean theorem is a consequence of the properties of the inner product:
where because of orthogonality.
A further generalization of the Pythagorean theorem in an inner product space to non-orthogonal vectors is the parallelogram law:
which says that twice the sum of the squares of the lengths of the sides of a parallelogram is the sum of the squares of the lengths of the diagonals. Any norm that satisfies this equality is ipso facto a norm corresponding to an inner product.
The Pythagorean identity can be extended to sums of more than two orthogonal vectors. If v1, v2, ..., vn are pairwise-orthogonal vectors in an inner-product space, then application of the Pythagorean theorem to successive pairs of these vectors (as described for 3-dimensions in the section on solid geometry) results in the equation
Sets of m-dimensional objects in n-dimensional space
Another generalization of the Pythagorean theorem applies to Lebesgue-measurable sets of objects in any number of dimensions. Specifically, the square of the measure of an m-dimensional set of objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space is equal to the sum of the squares of the measures of the orthogonal projections of the object(s) onto all m-dimensional coordinate subspaces.
In mathematical terms:
where:
- is a measure in m-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.).
- is a set of one or more non-overlapping m-dimensional objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space.
- is the total measure (sum) of the set of m-dimensional objects.
- represents an m-dimensional projection of the original set onto an orthogonal coordinate subspace.
- is the measure of the m-dimensional set projection onto m-dimensional coordinate subspace . Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace.
- is the number of orthogonal, m-dimensional coordinate subspaces in n-dimensional space (R) onto which the m-dimensional objects are projected (m ≤ n):
Non-Euclidean geometry
The Pythagorean theorem is derived from the axioms of Euclidean geometry, and in fact, were the Pythagorean theorem to fail for some right triangle, then the plane in which this triangle is contained cannot be Euclidean. More precisely, the Pythagorean theorem implies, and is implied by, Euclid's Parallel (Fifth) Postulate. Thus, right triangles in a non-Euclidean geometry do not satisfy the Pythagorean theorem. For example, in spherical geometry, all three sides of the right triangle (say a, b, and c) bounding an octant of the unit sphere have length equal to π/2, and all its angles are right angles, which violates the Pythagorean theorem because .
Here two cases of non-Euclidean geometry are considered—spherical geometry and hyperbolic plane geometry; in each case, as in the Euclidean case for non-right triangles, the result replacing the Pythagorean theorem follows from the appropriate law of cosines.
However, the Pythagorean theorem remains true in hyperbolic geometry and elliptic geometry if the condition that the triangle be right is replaced with the condition that two of the angles sum to the third, say A+B = C. The sides are then related as follows: the sum of the areas of the circles with diameters a and b equals the area of the circle with diameter c.
Spherical geometry

For any right triangle on a sphere of radius R (for example, if γ in the figure is a right angle), with sides a, b, c, the relation between the sides takes the form:
This equation can be derived as a special case of the spherical law of cosines that applies to all spherical triangles:
For infinitesimal triangles on the sphere (or equivalently, for finite spherical triangles on a sphere of infinite radius), the spherical relation between the sides of a right triangle reduces to the Euclidean form of the Pythagorean theorem. To see how, assume we have a spherical triangle of fixed side lengths a, b, and c on a sphere with expanding radius R. As R approaches infinity the quantities a/R, b/R, and c/R tend to zero and the spherical Pythagorean identity reduces to so we must look at its asymptotic expansion.
The Maclaurin series for the cosine function can be written as with the remainder term in big O notation. Letting be a side of the triangle, and treating the expression as an asymptotic expansion in terms of R for a fixed c,
and likewise for a and b. Substituting the asymptotic expansion for each of the cosines into the spherical relation for a right triangle yields
Subtracting 1 and then negating each side,
Multiplying through by 2R, the asymptotic expansion for c in terms of fixed a, b and variable R is
The Euclidean Pythagorean relationship is recovered in the limit, as the remainder vanishes when the radius R approaches infinity.
For practical computation in spherical trigonometry with small right triangles, cosines can be replaced with sines using the double-angle identity to avoid loss of significance. Then the spherical Pythagorean theorem can alternately be written as
Hyperbolic geometry

In a hyperbolic space with uniform Gaussian curvature −1/R, for a right triangle with legs a, b, and hypotenuse c, the relation between the sides takes the form:
where cosh is the hyperbolic cosine. This formula is a special form of the hyperbolic law of cosines that applies to all hyperbolic triangles:
with γ the angle at the vertex opposite the side c.
By using the Maclaurin series for the hyperbolic cosine, cosh x ≈ 1 + x/2, it can be shown that as a hyperbolic triangle becomes very small (that is, as a, b, and c all approach zero), the hyperbolic relation for a right triangle approaches the form of Pythagoras' theorem.
For small right triangles (a, b << R), the hyperbolic cosines can be eliminated to avoid loss of significance, giving
Very small triangles
For any uniform curvature K (positive, zero, or negative), in very small right triangles (|K|a, |K|b << 1) with hypotenuse c, it can be shown that
Differential geometry

The Pythagorean theorem applies to infinitesimal triangles seen in differential geometry. In three dimensional space, the distance between two infinitesimally separated points satisfies
with ds the element of distance and (dx, dy, dz) the components of the vector separating the two points. Such a space is called a Euclidean space. However, in Riemannian geometry, a generalization of this expression useful for general coordinates (not just Cartesian) and general spaces (not just Euclidean) takes the form:
which is called the metric tensor. (Sometimes, by abuse of language, the same term is applied to the set of coefficients gij.) It may be a function of position, and often describes curved space. A simple example is Euclidean (flat) space expressed in curvilinear coordinates. For example, in polar coordinates:
History

There is debate whether the Pythagorean theorem was discovered once, or many times in many places, and the date of first discovery is uncertain, as is the date of the first proof. Historians of Mesopotamian mathematics have concluded that the Pythagorean rule was in widespread use during the Old Babylonian period (20th to 16th centuries BC), over a thousand years before Pythagoras was born. The history of the theorem can be divided into four parts: knowledge of Pythagorean triples, knowledge of the relationship among the sides of a right triangle, knowledge of the relationships among adjacent angles, and proofs of the theorem within some deductive system.
Written c. 1800 BC, the Egyptian Middle Kingdom Berlin Papyrus 6619 includes a problem whose solution is the Pythagorean triple 6:8:10, but the problem does not mention a triangle. The Mesopotamian tablet Plimpton 322, written near Larsa also c. 1800 BC, contains many entries closely related to Pythagorean triples.
In India, the Baudhayana Shulba Sutra, the dates of which are given variously as between the 8th and 5th century BC, contains a list of Pythagorean triples and a statement of the Pythagorean theorem, both in the special case of the isosceles right triangle and in the general case, as does the Apastamba Shulba Sutra (c. 600 BC).
Byzantine Neoplatonic philosopher and mathematician Proclus, writing in the fifth century AD, states two arithmetic rules, "one of them attributed to Plato, the other to Pythagoras", for generating special Pythagorean triples. The rule attributed to Pythagoras (c. 570 – c. 495 BC) starts from an odd number and produces a triple with leg and hypotenuse differing by one unit; the rule attributed to Plato (428/427 or 424/423 – 348/347 BC) starts from an even number and produces a triple with leg and hypotenuse differing by two units. According to Thomas L. Heath (1861–1940), no specific attribution of the theorem to Pythagoras exists in the surviving Greek literature from the five centuries after Pythagoras lived. However, when authors such as Plutarch and Cicero attributed the theorem to Pythagoras, they did so in a way which suggests that the attribution was widely known and undoubted. Classicist Kurt von Fritz wrote, "Whether this formula is rightly attributed to Pythagoras personally ... one can safely assume that it belongs to the very oldest period of Pythagorean mathematics." Around 300 BC, in Euclid's Elements, the oldest extant axiomatic proof of the theorem is presented.
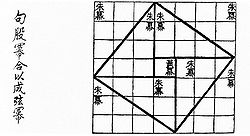
With contents known much earlier, but in surviving texts dating from roughly the 1st century BC, the Chinese text Zhoubi Suanjing (周髀算经), (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) gives a reasoning for the Pythagorean theorem for the (3, 4, 5) triangle — in China it is called the "Gougu theorem" (勾股定理). During the Han Dynasty (202 BC to 220 AD), Pythagorean triples appear in The Nine Chapters on the Mathematical Art, together with a mention of right triangles. Some believe the theorem arose first in China in the 11th century BC, where it is alternatively known as the "Shang Gao theorem" (商高定理), named after the Duke of Zhou's astronomer and mathematician, whose reasoning composed most of what was in the Zhoubi Suanjing.
See also
- Addition in quadrature
- At Dulcarnon – English phrase – at the end of one's wits
- British flag theorem
- Bride's Chair – Illustration of the Pythagorean theorem
- Fermat's Last Theorem
- Garfield's proof of the Pythagorean theorem
- Hsuan thu – Ancient Chinese diagram using the 3,4,5 right triangle to demonstrate the Pythagorean theoremPages displaying short descriptions of redirect targets
- Inverse Pythagorean theorem
- Kepler triangle
- Linear algebra
- List of triangle topics
- L space
- Nonhypotenuse number
- Parallelogram law
- Parseval's identity – The energy of a periodic function is the same in the time and frequency domain.
- Ptolemy's theorem – Relates the 4 sides and 2 diagonals of a quadrilateral with vertices on a common circle
- Pythagoras in popular culture
- Pythagorean expectation
- Pythagorean tiling
- Rational trigonometry in Pythagoras' theorem
- Thales theorem – On triangles inscribed in a circle with a diameter as an edgePages displaying short descriptions of redirect targets
Notes and references
Notes
- Van der Waerden believed that this material "was certainly based on earlier traditions". Carl Boyer states that the Pythagorean theorem in the Śulba-sũtram may have been influenced by ancient Mesopotamian math, but there is no conclusive evidence in favor or opposition of this possibility.
References
- ^ Judith D. Sally; Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. p. 63. ISBN 978-0-8218-4403-8.
- Benson, Donald. The Moment of Proof : Mathematical Epiphanies, pp. 172–173 (Oxford University Press, 1999).
- Euclid (1956), pp. 351–352
- Huffman, Carl (23 February 2005). "Pythagoras". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition)., "It should now be clear that decisions about sources are crucial in addressing the question of whether Pythagoras was a mathematician and scientist. The view of Pythagoras's cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus."
- Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4". Cut the Knot. Retrieved 4 November 2010.
- Alexander Bogomolny. "Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3". Cut the Knot. Retrieved 4 November 2010.
- (Loomis 1940)
- (Maor 2007, p. 39)
- Schroeder, Manfred Robert (2012). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Courier Corporation. pp. 3–4. ISBN 978-0486134789.
- See for example Pythagorean theorem by shear mapping Archived 2016-10-14 at the Wayback Machine, Saint Louis University website Java applet
- Jan Gullberg (1997). Mathematics: from the birth of numbers. W. W. Norton & Company. p. 435. ISBN 0-393-04002-X.
- Heiberg, J.L. "Euclid's Elements of Geometry" (PDF). pp. 46–47.
- "Euclid's Elements, Book I, Proposition 47". See also a web page version using Java applets by David E. Joyce, Clark University.
- Stephen W. Hawking (2005). God created the integers: the mathematical breakthroughs that changed history. Philadelphia: Running Press Book Publishers. p. 12. ISBN 0-7624-1922-9. This proof first appeared after a computer program was set to check Euclidean proofs.
- The proof by Pythagoras probably was not a general one, as the theory of proportions was developed only two centuries after Pythagoras; see (Maor 2007, p. 25)
- Alexander Bogomolny. "Pythagorean theorem, proof number 10". Cut the Knot. Retrieved 27 February 2010.
- (Loomis 1940, p. 113, Geometric proof 22 and Figure 123)
- Polster, Burkard (2004). Q.E.D.: Beauty in Mathematical Proof. Walker Publishing Company. p. 49.
- Published in a weekly mathematics column: James A Garfield (1876). "Pons Asinorum". The New England Journal of Education. 3 (14): 161. as noted in William Dunham (1997). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. p. 96. ISBN 0-471-17661-3. and in A calendar of mathematical dates: April 1, 1876 Archived July 14, 2010, at the Wayback Machine by V. Frederick Rickey
- Lantz, David. "Garfield's proof of the Pythagorean Theorem". Math.Colgate.edu. Archived from the original on 2013-08-28. Retrieved 2018-01-14.
- Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: pp. 106-107.
- Mike Staring (1996). "The Pythagorean proposition: A proof by means of calculus". Mathematics Magazine. 69 (1). Mathematical Association of America: 45–46. doi:10.2307/2691395. JSTOR 2691395.
- Bogomolny, Alexander. "Pythagorean Theorem". Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Archived from the original on 2010-07-06. Retrieved 2010-05-09.
- Bruce C. Berndt (1988). "Ramanujan – 100 years old (fashioned) or 100 years new (fangled)?". The Mathematical Intelligencer. 10 (3): 24–31. doi:10.1007/BF03026638. S2CID 123311054.
- Judith D. Sally; Paul J. Sally Jr. (2007-12-21). "Theorem 2.4 (Converse of the Pythagorean theorem).". Roots to Research. American Mathematical Society. pp. 54–55. ISBN 978-0-8218-4403-8.
- Euclid's Elements, Book I, Proposition 48 From D.E. Joyce's web page at Clark University
- Casey, Stephen, "The converse of the theorem of Pythagoras", Mathematical Gazette 92, July 2008, 309–313.
- Mitchell, Douglas W., "Feedback on 92.47", Mathematical Gazette 93, March 2009, 156.
- Ernest Julius Wilczynski; Herbert Ellsworth Slaught (1914). "Theorem 1 and Theorem 2". Plane trigonometry and applications. Allyn and Bacon. p. 85.
- Dijkstra, Edsger W. (September 7, 1986). "On the theorem of Pythagoras". EWD975. E. W. Dijkstra Archive.
- Alexander Bogomolny, Pythagorean Theorem for the Reciprocals,https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml
- Law, Henry (1853). "Corollary 5 of Proposition XLVII (Pythagoras's Theorem)". The Elements of Euclid: with many additional propositions, and explanatory notes, to which is prefixed an introductory essay on logic. John Weale. p. 49.
- Shaughan Lavine (1994). Understanding the infinite. Harvard University Press. p. 13. ISBN 0-674-92096-1.
- (Heath 1921, Vol I, pp. 65); Hippasus was on a voyage at the time, and his fellows cast him overboard. See James R. Choike (1980). "The pentagram and the discovery of an irrational number". The College Mathematics Journal. 11: 312–316.
- ^ Kurt Von Fritz (Apr 1945). "The Discovery of Incommensurability by Hippasus of Metapontum". Annals of Mathematics. Second Series. 46 (2): 242–264. doi:10.2307/1969021. JSTOR 1969021.
- Jon Orwant; Jarkko Hietaniemi; John Macdonald (1999). "Euclidean distance". Mastering algorithms with Perl. O'Reilly Media, Inc. p. 426. ISBN 1-56592-398-7.
- Wentworth, George (2009). Plane Trigonometry and Tables. BiblioBazaar, LLC. p. 116. ISBN 978-1-103-07998-8., Exercises, page 116
- Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron's Educational Series. p. 296. ISBN 0-7641-2892-2.
- WS Massey (Dec 1983). "Cross products of vectors in higher-dimensional Euclidean spaces" (PDF). The American Mathematical Monthly. 90 (10). Mathematical Association of America: 697–701. doi:10.2307/2323537. JSTOR 2323537. S2CID 43318100. Archived from the original (PDF) on 2021-02-26.
- Pertti Lounesto (2001). "§7.4 Cross product of two vectors". Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 96. ISBN 0-521-00551-5.
- Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover Publications. p. 24. ISBN 0-486-67002-3.
- Heath, T. L., A History of Greek Mathematics, Oxford University Press, 1921; reprinted by Dover, 1981.
- Euclid's Elements: Book VI, Proposition VI 31: "In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle."
- ^ Putz, John F. and Sipka, Timothy A. "On generalizing the Pythagorean theorem", The College Mathematics Journal 34 (4), September 2003, pp. 291–295.
- Lawrence S. Leff (2005-05-01). cited work. Barron's Educational Series. p. 326. ISBN 0-7641-2892-2.
- Howard Whitley Eves (1983). "§4.8:...generalization of Pythagorean theorem". Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0-88385-310-8.
- Aydin Sayili (Mar 1960). "Thâbit ibn Qurra's Generalization of the Pythagorean Theorem". Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603. S2CID 119868978.
- Judith D. Sally; Paul Sally (2007-12-21). "Exercise 2.10 (ii)". Roots to Research: A Vertical Development of Mathematical Problems. American Mathematical Soc. p. 62. ISBN 978-0-8218-4403-8.
- For the details of such a construction, see Jennings, George (1997). "Figure 1.32: The generalized Pythagorean theorem". Modern geometry with applications: with 150 figures (3rd ed.). Springer. p. 23. ISBN 0-387-94222-X.
- Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 77–78 (excerpt, p. 77, at Google Books)
- Rajendra Bhatia (1997). Matrix analysis. Springer. p. 21. ISBN 0-387-94846-5.
- For an extended discussion of this generalization, see, for example, Willie W. Wong Archived 2009-12-29 at the Wayback Machine 2002, A generalized n-dimensional Pythagorean theorem.
- Ferdinand van der Heijden; Dick de Ridder (2004). Classification, parameter estimation, and state estimation. Wiley. p. 357. ISBN 0-470-09013-8.
- Qun Lin; Jiafu Lin (2006). Finite element methods: accuracy and improvement. Elsevier. p. 23. ISBN 7-03-016656-6.
- Howard Anton; Chris Rorres (2010). Elementary Linear Algebra: Applications Version (10th ed.). Wiley. p. 336. ISBN 978-0-470-43205-1.
- ^ Karen Saxe (2002). "Theorem 1.2". Beginning functional analysis. Springer. p. 7. ISBN 0-387-95224-1.
- Douglas, Ronald G. (1998). Banach Algebra Techniques in Operator Theory (2nd ed.). New York, New York: Springer-Verlag New York, Inc. pp. 60–61. ISBN 978-0-387-98377-6.
- Donald R Conant & William A Beyer (Mar 1974). "Generalized Pythagorean Theorem". The American Mathematical Monthly. 81 (3). Mathematical Association of America: 262–265. doi:10.2307/2319528. JSTOR 2319528.
-
Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 2147. ISBN 1-58488-347-2.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
-
Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 0-521-85959-X.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- Stephen W. Hawking (2005). cited work. Running Press. p. 4. ISBN 0-7624-1922-9.
- Victor Pambuccian (December 2010). "Maria Teresa Calapso's Hyperbolic Pythagorean Theorem". The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- Barrett O'Neill (2006). "Exercise 4". Elementary Differential Geometry (2nd ed.). Academic Press. p. 441. ISBN 0-12-088735-5.
- Saul Stahl (1993). "Theorem 8.3". The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 0-86720-298-X.
- Jane Gilman (1995). "Hyperbolic triangles". Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0-8218-0361-1.
- Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0-521-65544-7.
- Neugebauer 1969, p. 36.
- Neugebauer 1969: p. 36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."
- Friberg, Jöran (1981). "Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations". Historia Mathematica. 8: 277–318. doi:10.1016/0315-0860(81)90069-0.: p. 306 "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period."
- Høyrup, Jens. "Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics". In Renger, Johannes (ed.). Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. pp. 393–407., p. 406, "To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors’ environment, possibly as a spin-off from the problem treated in Db2-146, somewhere between 2300 and 1825 BC." (Db2-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)
- Robson, E. (2008). Mathematics in Ancient Iraq: A Social History. Princeton University Press.: p. 109 "Many Old Babylonian mathematical practitioners … knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste ‘algebra’ on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia."
- Robson, Eleanor (2001). "Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322". Historia Mathematica. 28 (3): 167–206. doi:10.1006/hmat.2001.2317.
- Kim Plofker (2009). Mathematics in India. Princeton University Press. pp. 17–18. ISBN 978-0-691-12067-6.
- Bartel L. van der Waerden (2012). Geometry and Algebra in Ancient Civilizations. Springer Science & Business Media. p. 26.
- Carl Benjamin Boyer; Uta C. Merzbach (2011). "China and India". A history of mathematics (3rd ed.). Wiley. p. 229. ISBN 978-0470525487.
Quote: we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)
- Proclus (1970). A Commentary of the First Book of Euclid's Elements. Translated by Morrow, Glenn R. Princeton University Press. 428.6.
- "Introduction and books 1,2". The University Press. March 25, 1908 – via Google Books.
- (Heath 1921, Vol I, p. 144): "Though this is the proposition universally associated by tradition with the name of Pythagoras, no really trustworthy evidence exists that it was actually discovered by him. The comparatively late writers who attribute it to him add the story that he sacrificed an ox to celebrate his discovery."
- An extensive discussion of the historical evidence is provided in (Euclid 1956, p. 351) page=351
-
Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. p. 51. ISBN 0-88385-613-1.
...it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
- Robert P. Crease (2008). The great equations: breakthroughs in science from Pythagoras to Heisenberg. W W Norton & Co. p. 25. ISBN 978-0-393-06204-5.
- A rather extensive discussion of the origins of the various texts in the Zhou Bi is provided by Christopher Cullen (2007). Astronomy and Mathematics in Ancient China: The 'Zhou Bi Suan Jing'. Cambridge University Press. pp. 139 ff. ISBN 978-0-521-03537-8.
- This work is a compilation of 246 problems, some of which survived the book burning of 213 BC, and was put in final form before 100 AD. It was extensively commented upon by Liu Hui in 263 AD. Philip D. Straffin Jr. (2004). "Liu Hui and the first golden age of Chinese mathematics". In Marlow Anderson; Victor J. Katz; Robin J. Wilson (eds.). Sherlock Holmes in Babylon: and other tales of mathematical history. Mathematical Association of America. pp. 69 ff. ISBN 0-88385-546-1. See particularly §3: Nine chapters on the mathematical art, pp. 71 ff.
- Kangshen Shen; John N. Crossley; Anthony Wah-Cheung Lun (1999). The nine chapters on the mathematical art: companion and commentary. Oxford University Press. p. 488. ISBN 0-19-853936-3.
- In particular, Li Jimin; see Centaurus, Volume 39. Copenhagen: Munksgaard. 1997. pp. 193, 205.
- Chen, Cheng-Yih (1996). "§3.3.4 Chén Zǐ's formula and the Chóng-Chã method; Figure 40". Early Chinese work in natural science: a re-examination of the physics of motion, acoustics, astronomy and scientific thoughts. Hong Kong University Press. p. 142. ISBN 962-209-385-X.
- Wen-tsün Wu (2008). "The Gougu theorem". Selected works of Wen-tsün Wu. World Scientific. p. 158. ISBN 978-981-279-107-8.
Works cited
- Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0.
- Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. Vol. 1 (Books I and II). Translated by Heath, Thomas L. (Reprint of 2nd (1925) ed.). Dover. On-line text at archive.org
- Heath, Sir Thomas (1921). "The 'Theorem of Pythagoras'". A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 ff. ISBN 0-486-24073-8.
- Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 978-0-7637-4366-6. This high-school geometry text covers many of the topics in this WP article.
- Loomis, Elisha Scott (1940). The Pythagorean Proposition (2nd ed.). Ann Arbor, Michigan: Edwards Brothers. ISBN 9780873530361. Reissued 1968 by the National Council of Teachers of Mathematics. A lower-quality scan was published online by the Education Resources Information Center, ERIC ED037335.
- Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8.
- Neugebauer, Otto (1969). The exact sciences in antiquity (2nd ed.). Courier Dover Publications. ISBN 0-486-22332-9. OCLC 638685764.
- Robson, Eleanor and Jacqueline Stedall, eds., The Oxford Handbook of the History of Mathematics, Oxford: Oxford University Press, 2009. pp. vii + 918. ISBN 978-0-19-921312-2.
- Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. Also ISBN 3-540-96981-0.
- Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2.
- van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5.
Pythagorean triples Babylonian scribes van der Waerden.
External links
- Euclid (1997) . David E. Joyce (ed.). Elements. Retrieved 2006-08-30. In HTML with Java-based interactive figures.
- "Pythagorean theorem". Encyclopedia of Mathematics. EMS Press. 2001 .
- History topic: Pythagoras's theorem in Babylonian mathematics
- Interactive links:
- Interactive proof in Java of the Pythagorean theorem
- Another interactive proof in Java of the Pythagorean theorem
- Pythagorean theorem with interactive animation
- Animated, non-algebraic, and user-paced Pythagorean theorem
- Pythagorean theorem water demo on YouTube
- Pythagorean theorem (more than 70 proofs from cut-the-knot)
- Weisstein, Eric W. "Pythagorean theorem". MathWorld.
Categories:


 and which contain four right triangles whose sides are a, b and c, with the hypotenuse being c. In the square on the right side, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length c. Each outer square has an area of
and which contain four right triangles whose sides are a, b and c, with the hypotenuse being c. In the square on the right side, the triangles are placed such that the corners of the square correspond to the corners of the right angle in the triangles, forming a square in the center whose sides are length c. Each outer square has an area of  as well as
as well as  , with
, with  representing the total area of the four triangles. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length a and b. These rectangles in their new position have now delineated two new squares, one having side length a is formed in the bottom-left corner, and another square of side length b formed in the top-right corner. In this new position, this left side now has a square of area
representing the total area of the four triangles. Within the big square on the left side, the four triangles are moved to form two similar rectangles with sides of length a and b. These rectangles in their new position have now delineated two new squares, one having side length a is formed in the bottom-left corner, and another square of side length b formed in the top-right corner. In this new position, this left side now has a square of area 
 and
and  which will again lead to a second square of with the area
which will again lead to a second square of with the area 

 , while the small square has side b − a and area (b − a). The area of the large square is therefore
, while the small square has side b − a and area (b − a). The area of the large square is therefore








 , which is removed by multiplying by two to give the result.
, which is removed by multiplying by two to give the result.

 , which is a
, which is a 



 and
and  (a line from the right angle and perpendicular to the
(a line from the right angle and perpendicular to the  ). The Pythagorean theorem has,
). The Pythagorean theorem has,
 to the altitude
to the altitude 

 for any non-zero
for any non-zero  . If the
. If the  are to be
are to be  is then
is then

 . The reciprocal Pythagorean theorem is a special case of the
. The reciprocal Pythagorean theorem is a special case of the 
 are square numbers.
are square numbers.






 and
and  , is defined, by generalization of the Pythagorean theorem, as:
, is defined, by generalization of the Pythagorean theorem, as:





 The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.
The Pythagorean theorem, valid for right triangles, therefore is a special case of the more general law of cosines, valid for arbitrary triangles.







 where
where  is the angle between sides
is the angle between sides  and
and  .
.
 radians or 90°, then
radians or 90°, then  , and the formula reduces to the usual Pythagorean theorem.
, and the formula reduces to the usual Pythagorean theorem.








 be orthogonal vectors in R. Consider the n-dimensional simplex S with vertices
be orthogonal vectors in R. Consider the n-dimensional simplex S with vertices  . (Think of the (n − 1)-dimensional simplex with vertices
. (Think of the (n − 1)-dimensional simplex with vertices  not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs.
not including the origin as the "hypotenuse" of S and the remaining (n − 1)-dimensional faces of S as its "legs".) Then the square of the volume of the hypotenuse of S is the sum of the squares of the volumes of the n legs. is zero. The
is zero. The 


 because of orthogonality.
because of orthogonality.



 is a measure in m-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.).
is a measure in m-dimensions (a length in one dimension, an area in two dimensions, a volume in three dimensions, etc.). is a set of one or more non-overlapping m-dimensional objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space.
is a set of one or more non-overlapping m-dimensional objects in one or more parallel m-dimensional flats in n-dimensional Euclidean space. is the total measure (sum) of the set of m-dimensional objects.
is the total measure (sum) of the set of m-dimensional objects. represents an m-dimensional projection of the original set onto an orthogonal coordinate subspace.
represents an m-dimensional projection of the original set onto an orthogonal coordinate subspace. is the measure of the m-dimensional set projection onto m-dimensional coordinate subspace
is the measure of the m-dimensional set projection onto m-dimensional coordinate subspace  . Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace.
. Because object projections can overlap on a coordinate subspace, the measure of each object projection in the set must be calculated individually, then measures of all projections added together to provide the total measure for the set of projections on the given coordinate subspace. is the number of orthogonal, m-dimensional coordinate subspaces in n-dimensional space (R) onto which the m-dimensional objects are projected (m ≤ n):
is the number of orthogonal, m-dimensional coordinate subspaces in n-dimensional space (R) onto which the m-dimensional objects are projected (m ≤ n): 
 .
.


 so we must look at its
so we must look at its  with the remainder term in
with the remainder term in  be a side of the triangle, and treating the expression as an asymptotic expansion in terms of R for a fixed c,
be a side of the triangle, and treating the expression as an asymptotic expansion in terms of R for a fixed c,




 is recovered in the limit, as the remainder vanishes when the radius R approaches infinity.
is recovered in the limit, as the remainder vanishes when the radius R approaches infinity.
 to avoid
to avoid 






