| Revision as of 18:24, 24 August 2009 editSmackBot (talk | contribs)3,734,324 editsm Add references section and/or general fixes.← Previous edit | Revision as of 11:04, 29 August 2009 edit undoTimidGuy (talk | contribs)Extended confirmed users, Pending changes reviewers11,259 edits This sentence is out of place; and those early developers did not create the version described in this article; a popular book should not be used as a sourceNext edit → | ||
| Line 1: | Line 1: | ||
| {{ |
{{Unreferenced|date=July 2009}} | ||
| {{Expert-subject|Physics|date=November 2008}} | {{Expert-subject|Physics|date=November 2008}} | ||
| {{Cleanup|date=December 2006}} | {{Cleanup|date=December 2006}} | ||
| Line 39: | Line 39: | ||
| this model does not predicts ]. See ]. | this model does not predicts ]. See ]. | ||
| This theory was invented by ], with some collaboration by ] and ]. | |||
| This theory was first invented by ] in a paper published in 1982. <ref>S. M. Barr, Phys. Lett. B112 (1982) 219</ref> It was further described in a 1984 paper by J. P. Deredinger, J. E. Kim and ]<ref>J. P. Deredinger, J. E. Kim, D. V. Nanopoulos, Phys. Lett. B139 (1984) 170</ref> and a 1987 paper by I. Antoniadis, ], ] and Nanopoulos.<ref>I. Antoniadis, J. Ellis, J. Hagelin and D.V. Nanopoulos, Phys.Lett. B194 (1987) 231</ref><ref>Stenger, Victor J., ''Quantum Gods: Creation, Chaos and the Search for Cosmic Consciouness'', Prometheus Books (2009) ISBN-10: 1591027136 ISBN-13: 978-1591027133 p 61.</ref> | |||
| ] | ] | ||
| Line 111: | Line 111: | ||
| instead. These couplings do break the R-symmetry, though. | instead. These couplings do break the R-symmetry, though. | ||
| ==References== | |||
| {{Reflist}} | |||
| {{DEFAULTSORT:Flipped Su(5)}} | {{DEFAULTSORT:Flipped Su(5)}} | ||
Revision as of 11:04, 29 August 2009
| This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Flipped SU(5)" – news · newspapers · books · scholar · JSTOR (July 2009) (Learn how and when to remove this message) |
| This article needs attention from an expert in Physics. Please add a reason or a talk parameter to this template to explain the issue with the article. WikiProject Physics may be able to help recruit an expert. (November 2008) |
| This article may require cleanup to meet Misplaced Pages's quality standards. No cleanup reason has been specified. Please help improve this article if you can. (December 2006) (Learn how and when to remove this message) |
The Flipped SU(5) model is a GUT theory which states that the gauge group is:
Fermions form three families, each consisting of the representations
It is noticeable that this assignment includes three right-handed neutrinos, which are never been observed, but are often postulated to explain the lightness of the observed neutrinos and neutrino oscillations. There is also a and/or called the Higgs fields which acquire a VEV, yielding the spontaneous symmetry breaking
The SU(5) representations transform under this subgroup as the reducible representatio as follows:
- (u and l)
- (q, d and ν)
- (e)
- .
Comparison with the standard SU(5)
The name "flipped" SU(5) arose in comparison with the "standard" SU(5) model of Georgi-Glashow, in which and quark are respectively assigned to the 10 and 5 representation. In comparison with the standard SU(5), the flipped SU(5) can accomplish the spontaneous symmetry breaking using Higgs fields of dimension 10, while the standard SU(5) need both a 5- and 45-dimensional Higgs.
The sign convention for U(1)χ varies from article/book to article.
The hypercharge Y/2 is a linear combination (sum) of the of SU(5) and χ/5.
There are also the additional fields 5-2 and containing the electroweak Higgs doublets.
Of course, calling the representations things like and 240 is purely a physicist's convention, not a mathematician's convention, where representations are either labelled by Young tableaux or Dynkin diagrams with numbers on their vertices, but still, it is standard among GUT theorists.
Since the homotopy group
this model does not predicts monopoles. See Hooft-Polyakov monopole.
This theory was invented by Dimitri Nanopoulos, with some collaboration by John Hagelin and John Ellis.
Minimal supersymmetric flipped SU(5)
spacetime
The N=1 superspace extension of 3+1 Minkowski spacetime
spatial symmetry
N=1 SUSY over 3+1 Minkowski spacetime with R-symmetry
gauge symmetry group
/Z5
global internal symmetry
Z2 (matter parity) not related to U(1)R in any way for this particular model
vector superfields
Those associated with the SU(5)× U(1)χ gauge symmetry
chiral superfields
As complex representations:
| label | description | multiplicity | SU(5)× U(1)χ rep | rep | U(1)R |
| 10H | GUT Higgs field | 1 | 101 | + | 0 |
| GUT Higgs field | 1 | + | 0 | ||
| Hu | electroweak Higgs field | 1 | + | 2 | |
| Hd | electroweak Higgs field | 1 | + | 2 | |
| matter fields | 3 | - | 0 | ||
| 10 | matter fields | 3 | 101 | - | 0 |
| 1 | left-handed positron | 3 | 15 | - | 0 |
| φ | sterile neutrino (optional) | 3 | 10 | - | 2 |
| S | singlet | 1 | 10 | + | 2 |
Superpotential
A generic invariant renormalizable superpotential is a (complex) invariant cubic polynomial in the superfields which has an R-charge of 2. It is a linear combination of the following terms:
The second column expands each term in index notation (neglecting the proper normalization coefficient). i and j are the generation indices. The coupling Hd 10i 10j has coefficients which are symmetric in i and j.
In those models without the optional φ sterile neutrinos, we add the nonrenormalizable couplings
instead. These couplings do break the R-symmetry, though.
Categories:
 for the lepton doublet, L, and the up quarks
for the lepton doublet, L, and the up quarks  ;
; for the quark doublet,Q ,the down quark,
for the quark doublet,Q ,the down quark,  and the right-handed neutrino, N;
and the right-handed neutrino, N; for the charged leptons,
for the charged leptons, .
.
 called the Higgs fields which acquire a
called the Higgs fields which acquire a  to
to 
 (u and l)
(u and l) (q, d and ν)
(q, d and ν) (e)
(e) .
. of SU(5) and χ/5.
of SU(5) and χ/5.
 containing the
containing the 
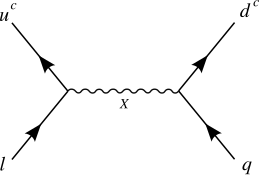
 boson
boson  in flipped
in flipped  GUT
GUT rep
rep



 invariant cubic polynomial in the superfields which has an R-charge of 2. It is a linear combination of the following terms:
invariant cubic polynomial in the superfields which has an R-charge of 2. It is a linear combination of the following terms:

