| Revision as of 20:49, 5 April 2013 edit74.114.87.73 (talk) →3D examplesTag: section blanking← Previous edit | Revision as of 20:49, 5 April 2013 edit undoAmcrius (talk | contribs)Extended confirmed users737 edits Reverted 1 edit by 74.114.87.73 (talk): Unexplained removal of content. (TW)Next edit → | ||
| Line 47: | Line 47: | ||
| Image:Param st 01.jpg|<center>'''i=1 j=2'''</center> | Image:Param st 01.jpg|<center>'''i=1 j=2'''</center> | ||
| </gallery> | </gallery> | ||
| ==3D examples== | |||
| ===Helix=== | |||
| ] | |||
| Parametric equations are convenient for describing ]s in higher-dimensional spaces. For example: | |||
| :<math>x = a \cos(t)\,</math> | |||
| :<math>y = a \sin(t)\,</math> | |||
| :<math>z = bt\,</math> | |||
| describes a three-dimensional curve, the ], which has a radius of ''a'' and rises by 2π''b'' units per turns. Note that the equations are identical in the ] to those for a circle. | |||
| Such expressions as the one above are commonly written as | |||
| :<math>r(t) = (x(t), y(t), z(t)) = (a \cos(t), a \sin(t), b t).\,</math> | |||
| ==Parametric surfaces== | ==Parametric surfaces== | ||
Revision as of 20:49, 5 April 2013

In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example uses a time parameter to determine the position, velocity, and other information about a body in motion.
Abstractly, a parametric equation defines a relation as a set of equations. Therefore, it is somewhat more accurately defined as a parametric representation. It is part of regular parametric representation.
2D examples
Parabola
For example, the simplest equation for a parabola,
can be parametrized by using a free parameter t, and setting
Circle
A more sophisticated example might be the following. Consider the unit circle which is described by the ordinary (Cartesian) equation
This equation can be parametrized as well, giving
With the Cartesian equation it is easier to check whether a point lies on the circle or not. With the parametric version it is easier to obtain points on a plot.

Some sophisticated functions
Other examples are shown:
3D examples
Helix

Parametric equations are convenient for describing curves in higher-dimensional spaces. For example:
describes a three-dimensional curve, the helix, which has a radius of a and rises by 2πb units per turns. Note that the equations are identical in the plane to those for a circle. Such expressions as the one above are commonly written as
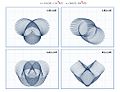
Parametric surfaces
A torus with major radius R and minor radius r may be defined parametrically as
where the two parameters t and u both vary between 0 and 2π.
As u varies from 0 to 2π the point on the surface moves about a short circle passing through the hole in the torus. As t varies from 0 to 2π the point on the surface moves about a long circle around the hole in the torus.
Usefulness
This way of expressing curves is practical as well as efficient; for example, one can integrate and differentiate such curves termwise. Thus, one can describe the velocity of a particle following such a parametrized path as:
and the acceleration as:
In general, a parametric curve is a function of one independent parameter (usually denoted t). For the corresponding concept with two (or more) independent parameters, see Parametric surface.
Another important use of parametric equations is in the field of computer aided design (CAD). For example, consider the following three representations, all of which are commonly used to describe planar curves.
| Type | Form | Example | Description |
|---|---|---|---|
| 1. Explicit | Line | ||
| 2. Implicit | Circle | ||
| 3. Parametric | ; |
|
Line Circle |
The first two types are known as analytical or nonparametric representations of curves, and, in general tend to be unsuitable for use in CAD applications. For instance, both are dependent upon the choice of coordinate system and do not lend themselves well to geometric transformations, such as rotations, translations, and scaling. In addition, the implicit representation is awkward for generating points on a curve because x values may be chosen which do not actually lie on the curve. These problems are eliminated by rewriting the equations in parametric form.
Conversion from two parametric equations to a single equation
Converting a set of parametric equations to a single equation involves eliminating the variable from the simultaneous equations . If one of these equations can be solved for t, the expression obtained can be substituted into the other equation to obtain an equation involving x and y only. If and are rational functions then the techniques of the theory of equations such as resultants can be used to eliminate t. In some cases there is no single equation in closed form that is equivalent to the parametric equations.
To take the example of the circle of radius a above, the parametric equations
can be simply expressed in terms of x and y by way of the Pythagorean trigonometric identity:
which is easily identifiable as a type of conic section (in this case, a circle).
See also
Notes
- Stewart, James (2003). Calculus (5th ed.). Belmont, CA: Thomson Learning, Inc. pp. 687–689. ISBN 0-534-39339-X.
- Shah, Jami J. (1995). Parametric and feature-based CAD/CAM: concepts, techniques, and applications. New York, NY: John Wiley & Sons, Inc. pp. 29–31. ISBN 0-471-00214-3.
{{cite book}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - See "Equation form and Parametric form conversion" for more information on converting from a series of parametric equations to single function.





























 ;
; 




 from the simultaneous equations
from the simultaneous equations  . If one of these equations can be solved for t, the expression obtained can be substituted into the other equation to obtain an equation involving x and y only. If
. If one of these equations can be solved for t, the expression obtained can be substituted into the other equation to obtain an equation involving x and y only. If  and
and  are rational functions then the techniques of the
are rational functions then the techniques of the 


