| Revision as of 15:46, 4 April 2021 editMarcocapelle (talk | contribs)Extended confirmed users, Page movers557,894 edits →References: more specific categorizationTags: Mobile edit Mobile web edit Advanced mobile edit← Previous edit | Revision as of 15:46, 4 April 2021 edit undoMarcocapelle (talk | contribs)Extended confirmed users, Page movers557,894 edits →References: fixTags: Mobile edit Mobile web edit Advanced mobile editNext edit → | ||
| Line 55: | Line 55: | ||
| {{DEFAULTSORT:Propositional Representation}} | {{DEFAULTSORT:Propositional Representation}} | ||
| ] | ] | ||
| ] | ] | ||
| ] | ] | ||
Revision as of 15:46, 4 April 2021
| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Propositional representation" – news · newspapers · books · scholar · JSTOR (March 2008) (Learn how and when to remove this message) |
Propositional representation is the psychological theory, first developed in 1973 by Dr. Zenon Pylyshyn, that mental relationships between objects are represented by symbols and not by mental images of the scene.
Examples
A propositional network describing the sentence "John believes that Anna will pass her exam" is illustrated below.

Each circle represents a single proposition, and the connections between the circles describe a network of propositions.
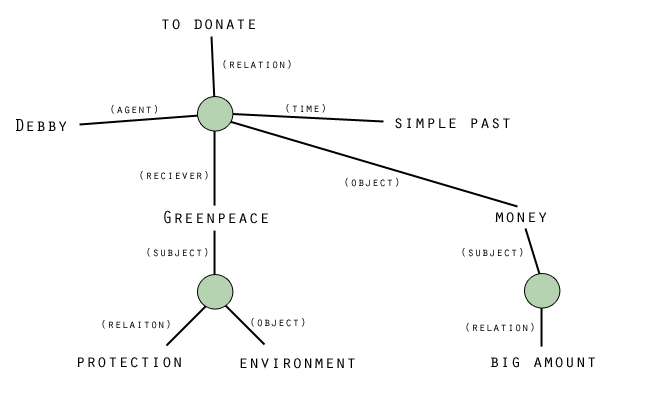
Another example is the sentence "Debby donated a big amount of money to Greenpeace, an organisation which protects the environment", which contains the propositions "Debby donated money to Greenpeace", "The amount of money was big" and "Greenpeace protects the environment". If one or more of the propositions is false, the whole sentence is false. This is illustrated in Figure 2:
Propositional representations are also:
- Language-like only in the sense that they manipulate symbols as a language does. The language of thought cannot be thought of as a natural language; it can only be a formal language that applies across different linguistic subjects, it therefore must be a language common to mind rather than culture, must be organizational rather than communicative. Thus Mentalese is best expressed through predicate and propositional calculus.
- Made up of discrete symbols; each symbol has a smallest constituent part; i.e. limit to how far units of rep. can be broken down.
- Explicit; each symbol represents something (object, action, relation) specifically and thus explicitly.
- Grammatical; symbolic manipulation follows (requires?) syntactical rules and semantical rules.
- Abstract and amodal; symbols may represent any ideational content irrespective of which sensory modality was involved in its perception. (Unlike a pictorial representation which must be modality specific to the visual sensory mode).
Each proposition consists of a set of predicates and arguments which are represented in the form of predicate calculus. For instance:
An event; (X) John hit Chris with a unicycle, the unicycle broke, because of this John started to cry, which caused Chris to be happy.
A propositional representation
- P
- Q
- R
- S
- Cause (Q, R)
- Cause (R, S)
Each set of predicates (words like hit, broke, cry, happy are first order-predicates; Cause is a second-order predicate) and arguments (often consisting of an agent/subject (e.g. John in ‘P’), a recipient/object (e.g. Chris in ‘P’) and an instrument (e.g. the unicycle in ‘P’)) are in turn manipulated as propositions: event/statement “John hit Chris with the unicycle” is represented as proposition ‘P’.
Also, features of particular objects may be characterized through attribute lists. ‘John’ as a singular object may have the attributes ‘plays guitar’, ‘juggles’, ‘eats a lot’, ‘rides a unicycle’ etc. Thus reference to ‘John’ identifies him as the object of thought in virtue of his having certain of these attributes. So in predicate calculus, if “John (F) has the property of being ‘rides a unicycle’ (x)” we may say salva veritate: (x)(Fx). These elements have been called semantic primitives or semantic markers/features. Each primitive may in turn form part of a propositional statement, which in turn could be represented by an abstract figure e.g. ‘P’. The primitives themselves play a crucial role in categorizing and classifying objects and concepts.
The meaningful relations between ideas and concepts expressed between and within the propositions are in part dealt with through the general laws of inference. One of the most common of these is Modus Ponens Ponendum (MPP), which is a simple inference of relation between two objects, the latter supervening on the former (P-›Q). Thus if we have two propositions (P, Q) and we assume a law of inference that relates to them both (P-›Q), then if we have P we must necessarily have Q. Relations of causation and may be expressed in this fashion, i.e. one state (P) causing (-›) another (Q)
So a purely formal characterization of the event (X) written above in natural language would be something like:
- P, Q (A)
- Q -› R (A)
- Q (A1)
- R (2,3 MPP)
- R -› S (A)
- S (4,5 MPP)
References
- Pylyshyn, Zenon W (1973). "What the mind's eye tells the mind's brain: A critique of mental imagery". Psychological Bulletin. 80: 1–36. doi:10.1007/978-94-010-1193-8_1. ISBN 978-94-010-1195-2.
- Elport, Daniel "Cognitive Psychology and Cognitive Neuroscience", Wikibooks, July 2007, accessed March 07, 2011.