| Revision as of 01:02, 21 November 2008 editTrovatore (talk | contribs)Autopatrolled, Extended confirmed users, Pending changes reviewers38,197 edits →Geometry stub template: in favor of images← Previous edit | Revision as of 01:10, 21 November 2008 edit undoDavid Eppstein (talk | contribs)Autopatrolled, Administrators227,011 edits →Geometry stub template: rNext edit → | ||
| Line 634: | Line 634: | ||
| ] (]) 23:44, 20 November 2008 (UTC) | ] (]) 23:44, 20 November 2008 (UTC) | ||
| ::While we're holding votes, here's another: is Topology Expert a troll or just an insufferable snob? ] would argue for the latter, I suppose, but it seems shocking to me that I would have to defend Euclidean geometry as a subject of interest here, or for that matter ], despite its unpopularity among more-serious-than-thou mathematicians. —] (]) 01:10, 21 November 2008 (UTC) | |||
| :0 I'm afraid to say. These images are simply ]s, with a vanishingly small information content. They lie more in the realm of graphic design than mathematics, attempting to convey to much information in a small space is doomed. I see no compelling reason why we need an image at all. The wording ''This geometry-related article is a stub. You can help Misplaced Pages by expanding it'' conveys all the essential information, any icon just serves as visual clutter. To be awkward I've removed the image entirely. Does this do the job? --] (]): 00:09, 21 November 2008 (UTC) | :0 I'm afraid to say. These images are simply ]s, with a vanishingly small information content. They lie more in the realm of graphic design than mathematics, attempting to convey to much information in a small space is doomed. I see no compelling reason why we need an image at all. The wording ''This geometry-related article is a stub. You can help Misplaced Pages by expanding it'' conveys all the essential information, any icon just serves as visual clutter. To be awkward I've removed the image entirely. Does this do the job? --] (]): 00:09, 21 November 2008 (UTC) | ||
Revision as of 01:10, 21 November 2008
Algebra stub template
I have seen the template:
(removed now that discussion is over becase otherwise this page would be classified as an 'algebra stub' once archived)
on several pages and I was wondering whether this template could be changed (this maybe a bit difficult and I don't know the rules so I am assuming that this can be done). The reason being is that it does not really reflect what 'algebra (modern)' is; rather it reflects high school algebra. Maybe in a way it reflects field theory (in a vague way!) but it does not reflect group theory very well. I think that there could be a more 'representive' symbol. Any opinions?
Topology Expert (talk) 11:20, 9 November 2008 (UTC)
- Yes, we can change the image if desired. One advantage of the square root symbol, even if it's not great, is that it's instantly recognizable by a fifth-grader. I don't know how you would make an image of similar size to represent more advanced concepts from modern algebra. And I'm afraid that if we had a picture that was supposed to represent something advanced, few people would be able to even tall what the picture meant. — Carl (CBM · talk) 12:56, 9 November 2008 (UTC)
- How about just using a picture of an equation. e.g. a*b=c This reflects binary operations. Delaszk (talk) 17:45, 9 November 2008 (UTC)
- An equation sounds good to me. --Tango (talk) 18:09, 9 November 2008 (UTC)
- How about just using a picture of an equation. e.g. a*b=c This reflects binary operations. Delaszk (talk) 17:45, 9 November 2008 (UTC)
But I am not sure that fifth-graders are supposed to understand this. Moreover, a fifth grader would probably interpret the symbol as 'high-school algebra' (which is rather reasonable for someone who has never heard of the subject). Perhaps we could still make it 'easy to understand' and 'representative of modern algebra'?
I agree with what User:Delaszk said because the most appropriate symbol would probably be one that reflects the fundamental idea behind group theory (and that is of course the binary operation). Could we implement this or do we need more people to agree?
Topology Expert (talk) 00:50, 10 November 2008 (UTC)
- Go ahead and implement it. If someone doesn't like it, they can always revert and we can discuss it further. --Tango (talk) 01:00, 10 November 2008 (UTC)
Topology Expert (talk) 07:57, 10 November 2008 (UTC)
Could someone please tell me how (and I could do it)?
Topology Expert (talk) 07:39, 15 November 2008 (UTC)
- How about that? It's the simplest equation I could find on commons Ben (talk) 09:22, 15 November 2008 (UTC)
- I think that image would be better for number theory (after all Fermat's last theorem is the most famous theorem of number theory). So I changed it. Topology Expert (talk) 05:43, 16 November 2008 (UTC)
- I think I prefer the old one actually. MSGJ 09:36, 15 November 2008 (UTC)
- I think that image would be better for number theory (after all Fermat's last theorem is the most famous theorem of number theory). So I changed it. Topology Expert (talk) 05:43, 16 November 2008 (UTC)
- The problem with a lot of "images" nowadays is that they aren't proper images. They use transparent colors or background colors, which means if your browser is set up to be be white text on black background then all these "images" disappear, including the main[REDACTED] logo. Delaszk (talk) 10:33, 15 November 2008 (UTC)
- I have finally changed the image to a more 'representative' one. Since modern algebra is based on the binary operation (just as topology is based on a topology), this certainly represents modern algebra and its 'close relative' (I think category theory first developed from a group theoretical model so this is what I mean by 'close relative') category theory.
- The previous image a^n + b^n = c^n was alright but it still did not represent modern algebra (more like Fermat's last theorem which I would classify as number theory). This looks much better and gives a better impression of mathematics(don't you hate it when people think that mathematics is about 'summing numbers up'?). Topology Expert (talk) 05:37, 16 November 2008 (UTC)
- By the way, I removed the template at the beginning of this discussion for otherwise this page would be classified as an 'algebra stub' once archived. Topology Expert (talk) 05:40, 16 November 2008 (UTC)
- The number theory one looks fine on this PC, but the algebra one is huge. See Affine Grassmannian for example, where the stub template is almost as big as the rest of the article. It may be just this computer, but it would be good if others could check this out please. Ben (talk) 06:15, 16 November 2008 (UTC)
- Thanks for the feedback. On my PC, it does not look as large. I will play around with the template a little to make it visible as well as small but anyhow this template is the 'best representative' of modern algebra (by the way, the previous (sqrt(x)) template was almost as big as this one). Topology Expert (talk) 06:22, 16 November 2008 (UTC)
- How about now (It think 200px is the minimum size possible without making it invisible to the naked eye)? Topology Expert (talk) 06:25, 16 November 2008 (UTC)
- Thanks for the feedback. On my PC, it does not look as large. I will play around with the template a little to make it visible as well as small but anyhow this template is the 'best representative' of modern algebra (by the way, the previous (sqrt(x)) template was almost as big as this one). Topology Expert (talk) 06:22, 16 November 2008 (UTC)
- The number theory one looks fine on this PC, but the algebra one is huge. See Affine Grassmannian for example, where the stub template is almost as big as the rest of the article. It may be just this computer, but it would be good if others could check this out please. Ben (talk) 06:15, 16 November 2008 (UTC)
- By the way, I removed the template at the beginning of this discussion for otherwise this page would be classified as an 'algebra stub' once archived. Topology Expert (talk) 05:40, 16 November 2008 (UTC)
I'm just wondering why these stub templates need images at all. Would not
- This algebra-related article is a stub. You can help Misplaced Pages by expanding it.
suffice. What encyclopedic purpose does the image really serve, they just take up screen space and distract the eye.--Salix (talk): 08:22, 16 November 2008 (UTC)
- TopExp, I understand the reasons you have for changing this image, but I think this one is too complicated and will distract people from the content of the article. It's too big, and as you say it can't be reduced without making the symbols unreadable. All we want is a simple image. MSGJ 08:46, 16 November 2008 (UTC)
- Thankyou for your opinions. I would not say that this template is too big (maybe a bit larger than the previous sqrt (x) template) and furthermore it gives a (fairly simple) representation of the binary operation using a commutative diagram. I can't see anything complicated about this image either (if someone understands what a commutative diagram is then he/she would probably understand the mathematics behind the template). Could we please just keep the image? I have even added that the image is not part of the article so there is no confusion and I don't think that it will distract people from the content of a particular article. See locally finite group for an example. In this article, the template fits in nicely.
- TopExp, I understand the reasons you have for changing this image, but I think this one is too complicated and will distract people from the content of the article. It's too big, and as you say it can't be reduced without making the symbols unreadable. All we want is a simple image. MSGJ 08:46, 16 November 2008 (UTC)
As I have mentioned already, a simple image such as sqrt(x) or a^n + b^n = c^n is representing the wrong field of maths (one representing arithmetic and the other is representing number theory). I can get a different image and try it out, perhaps, if other people also disagree entirely with this image. But I think (and I hope others do to) that we need a proper image and all the previous ones were not at all satisfactory.
Topology Expert (talk) 09:55, 16 November 2008 (UTC)
Take the current {{Cattheory-stub}} template which is basically (not mathematically) the same as this one.
Topology Expert (talk) 09:58, 16 November 2008 (UTC)
What about this one:
that illustrates the compatibility of two different structures on a field (that make it into a bialgebra). If not this one, I would say that the following image could also work (quite a simple commutative diagram that illustrates the associativity of monoids (assoicativity is something that a fourth grader could understand)):
Any opinions?
Topology Expert (talk) 10:42, 16 November 2008 (UTC)
- Now that I'm home and I've looked at this on my own computer, I am leaning towards not supporting this change. Even though the image is smaller than it was earlier, it's still much bigger than it should be. It seems to me these templates are designed to entice readers/editors to add to the article and help humans/bots to categorise them. Are there any other uses? If not, then I don't see that an image is going to make that much of a difference. An image may add a bit of life to otherwise bare articles, or they may help humans quickly refine a categorisation (maths stub -> algebra stub with a quick glance at a familiar image), but a massive commutative diagram isn't any better then a discrete square root symbol in these cases. I'm also worried about the notice, inside the template, telling people that the template isn't part of the article. Are most readers going to know what a template is? I've been here for three years and I'd still ask myself what this commutative diagram is doing here before realising it's part of the template. I think it's best to keep things simple here - a square symbol might not be the best representative for algebra, but surely it's good enough? Ben (talk) 10:47, 16 November 2008 (UTC)
- What about
- Jakob.scholbach (talk) 11:03, 16 November 2008 (UTC)
- That looks brilliant, but I thought there was some issues with that image? Or have they been resolved? Ben (talk) 11:08, 16 November 2008 (UTC)
- Well, if you look here, I think consensus is leaning towards keeping the image. I personally also think that the deletion discussion is pretty much nonsense. Jakob.scholbach (talk) 11:16, 16 November 2008 (UTC)
- That looks brilliant, but I thought there was some issues with that image? Or have they been resolved? Ben (talk) 11:08, 16 November 2008 (UTC)
Unfortunately, no one seems to understand my point. My point is that we want something that represents modern algebra. Not some junk like a square root symbol that makes an ordinary person believe that mathematics goes as far as a square root (and believe me, there are people who think this). Furthermore, this is not the sole purpose of the image. We also want the image to represent a fundamental idea behind group theory. I do like the image given by Jakob.scholbach, but a cube does not represent the fundamental idea behind group theory. A concept such as the binary operation or a commutative diagram that illustrates the compatibility of two different structures on a field would really represent this field of mathematics better (the binary operation would be the best). If you want something easier to understand (now lets face it, there are mathematicians who don't know much group theory (or category theory)), then choose something like this:
This commutative diagram represents the associativity of the binary operation in a monoid (which would be understood by any real mathematician). We definitely can't (and don't want to) aim for an average (non-mathematician) to understand the image; we want the image to be understood by someone who has had some decent formal training in mathematics (or who is learning group theory). And anyone who knows what a function is would probably understand a (simple rectangular) commutative diagram.
So if you don't like the current image, the one I just suggested may be better. Any opinions? If there is still disagreement, I can try for another image but I would like to have the opinions of several mathematicians.
Topology Expert (talk) 12:21, 16 November 2008 (UTC)
- I think I understand what you are after. I do think the Rubik's cube represents quite well what a group, and a fortiori a binary operation, is. For practical matters
- seems to me hardly useful, since one cannot decipher what it is about. Moreover, when I see a commutative diagram, I don't think of algebra first, more of category theory. Possibly one has to find some sort of compromise between easiness in grasping the image's content and conveying enough of the idea one has in mind. This can be very challenging (compare it to a three(!)-word explanation of a topic). Jakob.scholbach (talk) 12:30, 16 November 2008 (UTC)
Thanks for the opinion. What I don't understand is why we can't make the image 100px which is not too large and is still (reasonably) visible to the naked eye:
Why wouldn't this work?
With regards to algebra and category theory, I am quite confident when I say that category theory was invented based on algebra and then expanded to other fields of mathematics. For instance, 'isomorphism' is common to both fields and I can list quite a few others which are active terms in algebra as well as in category theory. If you analyse the commutative diagram carefully, it basically illustrates (the fact) that in a monoid, the binary operation is associative.
Topology Expert (talk) 12:57, 16 November 2008 (UTC)
As I mentioned earlier, one cannot decipher what the current category theory stub template is about either ({{Cattheory-stub}}) but that has been there for a long time. At least 100px is visible and not too large. Why in Misplaced Pages, does everything have to follow strict rules?
Topology Expert (talk) 12:59, 16 November 2008 (UTC)
- Well, I mean we can make it a little bit bigger, too. Nobody, however will "analyse the diagram carefully", people just glance at such things. Also, I think an undergrad guy or a physicist, say, will probably in general not know commutative diagrams at all. But as somebody said above, it is not terribly important what image we choose. The more important thing is to get the templates removed by writing sufficient articles. Jakob.scholbach (talk) 14:44, 16 November 2008 (UTC)
I agree with what you say about the importance of the image. But at least this image is better than sqrt(x) and I bet that someone who knows calculus could easily learn what a commutative diagram is. Furthermore, we don't expect everyone to understand it; as long as an algebraist can understand it, its fine. The image should just be a representation of the field and not part of an article, so people are not expected to understand the image.
Topology Expert (talk) 03:45, 17 November 2008 (UTC)
- To me the new image conveys the message that algebra = category theory. Is that accurate or desirable? —David Eppstein (talk) 04:05, 17 November 2008 (UTC)
- I guess you (as well as other mathematicians) see it that way but I don't. My initial purpose was to have an image like a*b = c but that does not really make much sense as it is. Instead I thought something more 'representative' such as assoiciativity of monoids which are fundamental in algebra (and other fields) would be appropriate. Mathematically, the current commutative diagram is equivalent to: Let (M,*) be a monoid and let a, b and c belong to M. Then, (a*b)*c = a*(b*c). This also works in semigroups but most people would probably interpret M as a monoid. So if you look at it that way, the image does not convey that algebra = category theory, but rather it represents a fundamental axiom in algebra (the other image regarding the compatibility of two different structures over a field that make it into a bialgebra could have worked but was more specialized and was probably a bit advanced for the general reader).
Topology Expert (talk) 06:05, 17 November 2008 (UTC)
- Why not a stylized ? Ozob (talk) 23:06, 17 November 2008 (UTC)
I can't believe there's serious debate over whether abstract algebra should be represented by a 75px image of a commutative diagram, no matter how algebraic the fact it encodes. The idea, in addition to being absurd from a visual design perspective, borders on the snobbish: why does the stub template have to represent some fact of "real" math, one phrased in a language that, admittedly, is not understood or appreciated by most students and a good number of practitioners? Anyone who sees this stub, however amateur at algebra, should understand that it's talking about something they might know; ask yourselves if, as undergraduates, you would have had that reaction to the associativity square. I think this point is amply supported by Topology Expert's own words: if a calculus student could "easily learn", or someone familiar with functions could "probably understand" a commutative diagram, then it is too complicated; we should not be arguing over whether the picture is potentially comprehensible, but whether it is thematically suitable. We may not care whether non-mathematicians get it, but we had better not be so elite as to dismiss college students (or, God forbid, analysts :) ).
Furthermore, category theory is totally unnecessary for understanding what algebra is about, and writing associativity as a commutative diagram is obfuscatory unless there's a more general game afoot. Granted, saying "algebra is square roots" is rather a dumbification, but not every level of abstraction below the One True Abstraction gives a misleading picture of the subject. Algebra, in itself, is a subject concerned with sets, elements, and operations, not objects and arrows (however much about the former they reflect), and understanding it at just that level is enough to, say, get you a Fields Medal, if you do it right. Ozob's suggestion is an excellent one: it expresses a fact basically characteristic of algebra (if you see a binary operation, and it's associative, then you are in the midst of defining an algebraic structure) in a concise way that, if you learned any algebra at all, you learned this first. Ryan Reich (talk) 01:23, 18 November 2008 (UTC)
- I'm on board with not doing the arrow-chasing, but I like the Rubik version better. More eye-catchy. Plus non-associative algebra is still algebra. --Trovatore (talk) 01:26, 18 November 2008 (UTC)
- I have to go but just one point: Most college students would know what a commutative diagram is; won't they? Also, objects and arrows are involved in every maths (most basic notation: f: X -> Y).
Topology Expert (talk) 04:05, 18 November 2008 (UTC)
- I suspect it's not even true that most college mathematics majors would know what a commutative diagram is. But as for "most college students": certainly not. —David Eppstein (talk) 04:13, 18 November 2008 (UTC)
- Everyone in this discussion appears to know what a commutative diagram is. Furthermore, some editors here are probably students (my assumption). I am not saying that someone has to know category theory (or even what it is) to be a mathematician but the image I have given is mathematically equivalent to the one given by User:Ozob.
Also, category theory is the centre of mathematics and every single branch of mathematics has objects and arrows anyhow.
Non-associative algebra may still be algebra but you will have to agree that associativity (except for closure of course) is the most fundamental axiom in algebra.
Topology Expert (talk) 04:38, 18 November 2008 (UTC)
- Lots of people in this discussion are grad students or worse, and no one here is one of those storied casual editors who drives by a stub and throws in his two cents, at whom one assumes the template (and all its connotations) are aimed. That's the group you want some instant recognition from. Even among mathematicians, the assertion that there are always objects and arrows is probably going to raise some eyebrows; I mean, by that standard you can express Riemannian geometry as and other silliness. What you are arguing is the philosophical complement of what you started out denouncing: first the tag was oversimplified to the point of being misleadingly trivial; you now explicitly advocate it being overgeneralized to the point of being obscuringly deep.
- Now, my life situation being what it is I can't but agree that category theory is the bomb, but I don't think that point can be argued in an icon attached to a cleanup tag, and believe me when I say that most people, even mathematically-inclined people, would not understand it in the spirit you intend it. Ryan Reich (talk) 05:39, 18 November 2008 (UTC)
- Point: I don't say mathematics is about objects and arrows; I say that objects and arrows are there everywhere in mathematics. Topology Expert (talk) 06:26, 18 November 2008 (UTC)
- I have learnt one thing from this overwhelmingly long discussion: In Misplaced Pages, there is too much talk and too little action. Why waste time creating talk pages and discussing when by the time the discussion is over, people forget what they wanted to do initially (or what they were discussing about)? In my opinion, this discussion was a waste of time (for everyone). If people really hate the commutative diagram, I can let them have their way. But I have been in this discussion too long to give up.
Take this massive comutative diagram for instance:
How else would you describe what a Hopf algebra is (unless you want to tediously find a series of equations that are equivalent to this commutative diagram)? Commutative diagrams are a easy (and natural) way of storing information and are everywhere in advanced mathematics. I am probably telling you what you already know, but my point is that you shouldn't be afraid to include a commutative diagram in a supposedly 'lower level' mathematics like algebra. Furthermore, I can also bet you that everyone who knows algebra well, will also know what a commutative diagram is. Isn't that what we want?
Topology Expert (talk) 06:44, 18 November 2008 (UTC)
- Nobody is arguing (here) that category theory is somehow a waste of time. But that's beside the point. We have a separate stub sorting category for category theoretic stubs. Shouldn't we be aiming for something that would set algebra apart a little more from that? And besides, the diagrams fit very badly into the small size. I like the a(bc)=(ab)c idea expressed earlier, or even the Rubik's cube one, much better. —David Eppstein (talk) 06:49, 18 November 2008 (UTC)
- The Rubik's cube is far and away the best. You can't code any serious information about the subject into a stub image, and it's nice for them to be visually distinctive. --Trovatore (talk) 09:02, 18 November 2008 (UTC)
- The Rubik's cube gets my vote as well. MSGJ 09:11, 18 November 2008 (UTC)
- The Rubik's cube is far and away the best. You can't code any serious information about the subject into a stub image, and it's nice for them to be visually distinctive. --Trovatore (talk) 09:02, 18 November 2008 (UTC)
- Some of you are contradicting yourselves. First, you say that you don't want a commutative diagram because it is distracting and eye-catchy; now you are saying that you want something eye-catchy like a Rubik's cube. I don't mean to attack but I vote for at least as User:Ozob mentioned if not a commutative diagram. Associativity is fundamental and a Rubik's cube is rubbish (we are dealing with all forms of algebra; not just finite group theory).
Topology Expert (talk) 02:00, 19 November 2008 (UTC)
- Well, it's not like everyone who doesn't like the diagram idea has to agree on exactly why. But as far as I'm concerned, the problem with the diagram isn't that it draws too much attention to itself. It's that it draws attention to itself in a bad way — the likely reader reaction is "what the heck is that smudge?". Whereas the cube is instantly recognizable and visually attractive.
- As for "associativity being fundamental" to algebra, so you don't accept the octonions as an algebraic structure? --Trovatore (talk) 02:10, 19 November 2008 (UTC)
- Just to take the tangential mathematics off the table: octonions: algebraic, yes; fundamental, maybe not; associative, definitely not, but the absence being notable makes it just as important as a negative property. A lot of the exotic algebraic structures (e.g. Moufang loops) are premised on some compensation for nonassociativity. Ryan Reich (talk) 03:01, 19 November 2008 (UTC)
- Well, that's a little convoluted as a reason to include the associative law on a stub involving the octonions. But that isn't my real objection; it's just a response to TE. My real objection is that it's boring and formalistic-looking. (Unfortuately for {{mathlogic-stub}} I wasn't able to think of anything that wasn't boring and formalistic-looking; for algebra we have a good candidate and should use it.) --Trovatore (talk) 03:08, 19 November 2008 (UTC)
- Maths is not suppose to look fancy. Keeping things like a Rubik's cube gives the wrong impression about mathematics (people may think that the Rubik's cube is the highest level math there is). As for associativity, I never said that all algebraic strucutures are associative; most algebraic structures are and that is exactly why associativity is fundamental. Are you saying that it is not?
(By the way, associativity is to groups as Hausdorff is to topological spaces. Many mathematicians don't care about non-Hausdorff spaces but that does not mean that Hausdorff spaces are unimportant).
Topology Expert (talk) 03:28, 19 November 2008 (UTC)
Why would you think that is boring? When I first learnt about these infinite cardinalities, I was fascinated (and excited to prove by myself that ).
Topology Expert (talk) 03:35, 19 November 2008 (UTC)
- I certainly didn't say (the object) is boring! It's the symbol for it that's not terribly inspiring. Still, it does have some visual interest, with the Hebrew calligraphy — the associative-law thing doesn't even have that. --Trovatore (talk) 05:07, 19 November 2008 (UTC)
- Sorry about the misinterpretation. I think that after maybe 50 years, about every mathematician will read Misplaced Pages (even sooner perhaps). Algebra, as you will probably agree, is the most widely known (as in well-understood) mathematical subject (apart from calculus) by mathematicians. By putting this tag (commutative diagram) we are encouraging mathematicians (and college students) to find out what it is about and this will certainly make category theory more widely known. Isn't this what we want? The bonus is that it still has a lot to do with algebra.
Topology Expert (talk) 05:15, 19 November 2008 (UTC)
Great! I just thought of something much better (represents algebra well, very easy to understand, and also quite important)! What about an exact sequence? We could choose a simple sequence consisting only of three objects. For instance:
Practically everyone knows that represents the integers and practically everyone has a vague idea as to what the arrows are (a function). This would be more exciting as an image, more concise, and much better than a dinosaur commutative diagram. Any opinions on whether or not this would be preferable to a commutative diagram?
Topology Expert (talk) 05:28, 19 November 2008 (UTC)
- It's probably a bit better than the commutative diagram, if only because it's easier to read (the aspect ratio is a bit wide, though). But it's not as good as the Rubik's cube. No purely symbolic token is going to be. --Trovatore (talk) 05:33, 19 November 2008 (UTC)
- I suppose it is not as good as the cube because the cube is colourful. If you notice, every stub template in mathematics is a symbolic token (except for the geometry stub template). Why not follow this convention?
As I mentioned, we want to expand people's knowledge (one purpose of Misplaced Pages) and this stub template is excellent for this (allows people to learn about the mathematical subject of category theory).
Topology Expert (talk) 05:46, 19 November 2008 (UTC)
Well, if I were feeling cynical, I could point out that most of the students in a course I'm teaching never heard of Euclid until I mentioned his name (I don't know how you can do that and be a high-school graduate) and they certainly don't know what the blackboard bold letter Z represents. And guess what they "know" that the arrows mean? Here's an example:
That what "almost everybody knows" the arrows mean. Michael Hardy (talk) 05:54, 19 November 2008 (UTC)
There are two things that I have learnt in the past 10 days:
a) Misplaced Pages can be a big waste of time sometimes (good fun though)
b) The world is a lot dumber than I thought
(you must really get sick of teaching your students; I don't know how you do it)
Topology Expert (talk) 06:31, 19 November 2008 (UTC)
The Rubik's cube has the following flaws:
1. It is too colourful and gives the wrong impression of mathematics (people may think that to solve a Rubik's cube, you need to be good at maths and if you can solve it, you must be the best mathematician around (believe me, people think this already; we don't want to give them encouragement)).
2 (more importantly). It only represents finite group theory and does not have a wide scope. One user mentioned that the commutative diagram only represents associative algebra; at least it represents a wider scope of algebra compared to the Rubik's cube.
Any arguments against my points? (some support would be much appreciated)
Topology Expert (talk) 08:06, 19 November 2008 (UTC)
Because of the apparent stupidity of the outside world, I want to make a point that this template should only be aimed at real mathematicians (any mathematician knows what an exact sequence is (or at least what an arrow means (or Z (hopefully)))).
Topology Expert (talk) 08:11, 19 November 2008 (UTC)
- No, it shouldn't only be aimed at real mathematicians. It should be aimed at anyone who can expand the algebra stub. Knowing what a commutative diagram, exact sequence or arrow represents are not prerequisites to this. Honestly, people aren't going to take anything away from the image, instead they will take away something from the text "This is an algebra stub ...". We shouldn't be worried about the image representing all of algebra any more than an author worries about an image on the cover of their book representing all of its contents. It's just for show, so a simple representative should be fine. Ben (talk) 09:57, 19 November 2008 (UTC)
- I second that. What we need to do is just stop gabbing on about it and do something. Real mathematicians go home. What has category theory ever done for us ? Brwian (talk) 12:41, 19 November 2008 (UTC)
- Just answer this to yourself: don't you want people to understand what mathematicians do? Aren't you sick and tired of non-mathematicians confidently saying that mathematics is only about numbers and arithmetic? Well I am. All I want to do with this is:
a) Give an image which people (who don't know maths) are clueless about so they stop talking nonsense
b) Give an image which is really important in the intersection of mathematics with algebra
Commutative diagrams are wonderful for both purposes. As I mentioned, the image that User:Ozob suggested is mathematically equivalent to the commutative diagram and furthermore, gives more meaning to mathematics.
You are probably sick and tired of me arguing so I won't argue for so long. I just wanted to emphasise that:
a) The Rubik's cube is unsatisfactory (in my opinion) for the reasons I have already mentioned
b) User:Ozob's image is mathematically equivalent to mine
(You probably don't want me arguing any longer and as you said, it doesn't matter what image we choose; the words are more important. Since no one (except for me) is going to analyse the image, we might as well keep the commutative diagram unless of course it discourages people from expanding a stub (which is unlikely)).
I just wanted to make one quick (and very important point); algebra is a subject which almost any mathematician (and student) knows at least a little bit about. Therefore (with the number of algebraists around), any algebra stubs must contain really deep concepts within the field (because very few people would have known enough to expand it and hence it is a stub). So really, anyone who can expand an algebra stub, will probably know algebra well and hence what a commutative diagram is. The more simpler concepts can be edited by college students because they won't be stubs (generally between stub and good article mostly).
Topology Expert (talk) 12:45, 19 November 2008 (UTC)
Also (to Brwian), category theory is very important in mathematics (see category theory and perhaps homological algebra for an example). Topology Expert (talk) 12:54, 19 November 2008 (UTC)
- Homological algebra ? Well of course homological algebra! That goes without saying. But apart from homological algebra, what has category theory ever done for us ? Brwian (talk) 13:46, 19 November 2008 (UTC)
- Don't you want people to understand what mathematicians do? Aren't you sick and tired of non-mathematicians confidently saying that mathematics is only about numbers and arithmetic?
- I don't really worry about what they think, but regardless of what I worry about, I do think the mathematics pages here (as opposed to a small image attached to a minor template sitting at the bottom of a select few pages) are more than enough to convince them otherwise. Now, I'm not quite sure I follow your argument. You list 'ignorance of mathematics' as a motivating factor for this image change, but earlier you said these stub templates should be designed for real mathematicians. Now you're arguing that only advanced topics are stubs, but a quick scan of the algebra stubs shows plenty of 'basic' to undergraduate topics, Trinomial for instance. I don't think there is any good reason to think your proposal will change a single persons mind, but if any user points to one of the stub tag images and proclaims "See, mathematics is just numbers, arithmetic and Rubik's cubes!!", I'll gladly eat my words :) Ben (talk) 13:33, 19 November 2008 (UTC)
To Brwian: what about sheaf theory?
Topology Expert (talk) 02:54, 20 November 2008 (UTC)
OK, so there are a few basic concepts which are stubs. If I make them 'unstubs' now, we can accept the commutative diagram? I will start with trinomial.
Topology Expert (talk) 02:58, 20 November 2008 (UTC)
- You keep missing the point. The diagram doesn't look good. It's not a sensible idea to try to use the image in a stub template to stimulate interest in a subject; that's beyond its scope. The point of the image is to distinguish the various stub types with an appealing, and at least somehow relevant, icon. You're trying to read (or write) way too much into it. --Trovatore (talk) 03:42, 20 November 2008 (UTC)
(edit conflict) Most of the users have bailed this discussion so I think the vote is pretty much, 'who cares', although some users still strongly hate the commutative diagram. My point is that the commutative diagram encourages editors to learn about category theory. Have a look at this and you will find that the template is more descriptive and people will not think that it is a smudge anymore. Furthermore, the new description encourages readers to learn about category theory: a bonus because anyone who knows calculus (well, unlike Michael Hardy's students) will be able to learn the basics of category theory.
Topology Expert (talk) 03:50, 20 November 2008 (UTC)
- Please understand that I understand your comments. However, this diagram still represents algebra and anyway, all mathematics is based on category theory. So why not keep an image like that? Besides, the icon is still relevant.
Topology Expert (talk) 04:06, 20 November 2008 (UTC)
- I'm sorry, but that picture just says "category theory" to me. And no, I do not agree that algebra (as a whole) and category theory (as a whole) are in any way fundamental parts of each other. Why the intense insistence on using the template for advocacy? The stub template is not even really a part of the encyclopedia; people are not expected to learn anything from it, but simply be alerted that the article could be expanded. Putting in a lofty emblem says to the less fluent, "We really meant that someone smarter should improve this article", and to the more fluent, "There really isn't any point improving this article unless you can put in some commutative diagrams". Simply, the notions of category theory are not common indicators for algebra, so they will be received as requesting similarly uncommon response. As they sometimes say it, this kind of picture is POV (and this discussion proves it).
- As you can see, not everyone has "bailed", and from what I read in the more recent responses, the vote (which it is presumptuous for you to summarily dismiss in your favor) is unanimously (minus one) "No, don't use the diagram. It's ugly, confusing, philosophically overburdened, and wrongheaded." It may have been said politely in various roundabout ways, but there it is. Ryan Reich (talk) 04:13, 20 November 2008 (UTC)
- Update: I have put the associativity equation into {{algebra-stub}}. Maybe it's not ideal, but you are the only one who thinks it is less ideal than your commutative diagram, which it replaces. Ryan Reich (talk) 04:18, 20 November 2008 (UTC)
- I find your response quite rude. My intentions were good and I seem to have wasted my time trying to find a good image for nothing (I even tried to reason with something apart from the commutative diagram). Obviously, none of what I have done is appreciated.
Topology Expert (talk) 04:49, 20 November 2008 (UTC)
- I have responded on your talk page, since this is now a private matter. Ryan Reich (talk) 05:35, 20 November 2008 (UTC)
I have a better idea. There was no agreement over which image to use (some people liked the rubik's cube, some preferred the associative rule, some people don't give a monkeys). However there does seem to be consensus that the image is not very important - it's the text that is important. So I have removed the image and just left the text. I agree this discussion has gone on far too long. TE it is understood that your intentions are entirely good; however you should have realised earlier that your opinions were not gaining support. MSGJ 09:53, 20 November 2008 (UTC)
- Well I realized after I had argued for one page (ask yourself what you would have done in the same situation if you had argued for that long and, more importantly, strongly believed that the image was appropriate).
- However, I prefer User:Ozob's image and so does User:Ryan Reich. If you strongly don't want that image, hold a vote but I think for know I will keep the image Ryan chose. Hopefully, in the future when more mathematicians participate, I will get more support and then I may change the image. But I will leave it for now.
Topology Expert (talk) 11:17, 20 November 2008 (UTC)
- I've changed the equation from a statement into a question since there are plenty of interesting nonassociative algebras. In particular I've just come across gyrovector spaces, a brilliant way of looking at hyperbolic geometry and special relativity. P.S. I studied maths, but none of the courses were on category theory. As an aside, it does seem interesting that Galois theory can be generalized into a purely category theoretic setting, not that I understand any of it. ("Galois Theories", Francis Borceux, George Janelidze, Cambridge University Press, 2001) Delaszk (talk) 18:54, 20 November 2008 (UTC)
- In my opinion that equation is just too big and distracts. Perhaps we could make a decision on this and close this ridiculous thread? MSGJ 19:10, 20 November 2008 (UTC)
So in TE's style, please type below: (No reasons/discussion required, thanks.)
- 0, for no image at all
- 1, for the Rubik's cube
- 2, for the associativity equation (with or without the question mark)
- 3, for other (but unless the others can agree it's not going to win)
Votes will be counted tomorrow. MSGJ 19:12, 20 November 2008 (UTC)
- I vote 3 for . This includes both associative and nonassociative operations. Delaszk (talk) 20:11, 20 November 2008 (UTC)
- I vote for 1, the Rubik's cube. Eye-catching, instantly recognizable, and vaguely on-topic is better in this very restricted context than mathematical accuracy. But my second choice would be for 2, the associativity equation. —David Eppstein (talk) 21:51, 20 November 2008 (UTC)
- I say the Rubik's cube. It's a waste of oxygen to argue about the deeper meanings of template images; the important criteria are distinctiveness and aesthetic appeal. Of course it should also have something to do with the topic, but as long as there's a connection, we don't have to argue about the details of the connection. --Trovatore (talk) 21:58, 20 November 2008 (UTC)
- 2, associativity, no question mark. We just ended one debate about using a mathematical in-joke and now another is proposed? And Rubik's cube is too distinctive for my taste. Ryan Reich (talk) 23:26, 20 November 2008 (UTC)
- 1. The associtivity equation(s) might be better from a mathematical point of view, but it's too big and distracting to be placed on pages will little content. The cube is recongnisable even when it's tiny. Ben (talk) 23:31, 20 November 2008 (UTC)
- Anyone of them (I don't really care which one is chosen now. If it really matters, we can review the image after 6 months or so (when there are more voters)). But I just wanted to make a note about 'associative' and 'non-associative' algebra; earlier, the image was sqrt (x). Did that represent modern algebra at all? Take the Rubik's cube. Does that represent anything apart from group theory (or even finite group theory)?
Topology Expert (talk) 23:53, 20 November 2008 (UTC)
Show/hide button not working
In the "solution by algebra" section in Regiomontanus' angle maximization problem, I've put in a show/hide button that's not working. Can anyone figure out why? Michael Hardy (talk) 20:16, 10 November 2008 (UTC)
- I'm not sure why you want to use {{show}} in article space, but the problem seems to be equals signs being interpreted as template parameters. Geometry guy 20:37, 10 November 2008 (UTC)
Why I want to do it would be clear from what I wrote there, I would think. I know others have done this in various other math articles. Has this problem occurred elsewhere? Michael Hardy (talk) 22:06, 10 November 2008 (UTC)
- I appreciate your thanks for the fix. The articles linking to {{show}} are here. The obvious mathematical one is Mathematical induction, where the idea was introduced here. Do others think that this practice is a good idea? We show/hide navigation templates, comments, discussions, debates. Should we be doing this with content? Geometry guy 23:29, 10 November 2008 (UTC)
- Personally I do not support the use of hidden content within articles. When the issue is that certain boring derivations take up too much space, the solution is usually to remove the derivations. Unless there is some encyclopedic interest in a proof or derivation, it should be omitted. But if there is encyclopedic interest, then the derivation shouldn't be hidden from sight by default. — Carl (CBM · talk) 00:12, 11 November 2008 (UTC)
- No I don't think its good in article space. It breaks the dominant navigation metaphor where clicking on a link takes you to a new page and hence requiring special explination. --Salix (talk): 00:49, 11 November 2008 (UTC)
- Sometimes clicking on a link takes you to another place on the same page. The major thing I'd have against it is that some people switch off javascript and currently it looks like the default is that such people have the text hidden and can't show it. I'm sure they could fix it somehow so the default would be that if one has no javascript the text is shown. So basically my only objection is people haven't done it, rather they put the text into a section further down like an appendix or to another article and link to that. I think I could grow to like it if it was introduced as a general idea. Dmcq (talk) 02:24, 11 November 2008 (UTC)
It's not about hiding "boring derivations"; it's about hiding things that interrupt the main line of argument that is the point of the section or paragraph or passage, but that might nonetheless be of encyclopedic interest.
Also we have a policy requiring articles to be accessible to a broad audience. This furthers that policy. Michael Hardy (talk) 03:36, 11 November 2008 (UTC)
- I agree with Carl and others above. Jakob.scholbach (talk) 10:00, 11 November 2008 (UTC)
- A suggestion - a simpler derivation is
- - which is simply an application of completing the square - and then note that as x is always positive, the first term takes a minimum value of 0 when . Then the whole section in question can be omitted. Gandalf61 (talk) 10:50, 11 November 2008 (UTC)
- How is that simpler? It's the same thing except that you're working only with the numerator, and it's LONGER than why I wrote in the article (as long as you don't expand the hidden content). Michael Hardy (talk) 17:17, 11 November 2008 (UTC)
- It's simpler because it replaces the whole hidden section with one line and it doesn't introduce . But 'scuse me for trying to help you with a suggestion - next time I won't bother. Gandalf61 (talk) 22:58, 11 November 2008 (UTC)
- I don't see how it replaces the hidden section. It's clear how you go from right to left in the equality
- but many people will still wonder how you go from left to right. And that's what the hidden section explains. Michael Hardy (talk) 18:05, 16 November 2008 (UTC)
- I don't see how it replaces the hidden section. It's clear how you go from right to left in the equality
- Re M. Hardy: in many cases, we can "write around" the derivations, as would be done in regular published mathematics, so that readers who want to skip the derivations can just skip to the next paragraph.
- When I was talking about "boring derivations" I was referring to the reader's view; I should have found a better way to say it. Both examples I have seen of the use of hidden content involved relatively basic algebraic manipulations, rather than deep content. So I'm not convinced that they need to be in the article, even for accessibility (this is the ancient textbook/encyclopedia controversy). But if they do warrant inclusion, I think they should just be included, even if it requires some work to write compelling prose around them.
- Another option for including parenthetical comments is to put them in footnotes. Then they are not in the middle of the section, but also are not "hidden". — Carl (CBM · talk) 14:24, 11 November 2008 (UTC)
- Putting the derivations in a special footnote section at the bottom of the page is a good idea. You might consider using the "group=" property of the ref and references tags to handle derivations independently of the normal inline citations and footnotes. For example, you could write < ref group="derivation" > I've added an example to this sandbox.
- Here's another compromise that you all might consider. A little context first: at the Accessibility project, we've been discussing how to make math-mode text accessible to visually-impaired users, who rely on screen readers such as JAWS to hear Misplaced Pages articles. The simplest two solutions seem to be (1) don't use the math tag (rather draconian), or (2) add ALT text in the math-mode material as in the formula
- A third approach with potential is to introduce internal structure to math formulas so that scripts could act on them, to produce accessible ALT text automatically and, more ambitiously, to carry out various symbolic math calculations. This third approach can work for showing derivations as well. To illustrate this approach, I've written a prototype script User:Proteins/showmathderivations.js that you can import into your monobook.js page, which you can test out on this sandbox. It produces a tab labeled "d" at the top of the page, next to the "watch" tab. When clicked, the script displays the derivation in a popup window. The derivation itself is encoded in the page; in the sandbox, it's done explicitly, but I'm sure that you all see that it could be done very easily with templates. This gives students and other interested people the chance to see the derivation, whereas uninterested people need not even notice its existence. Nor would the derivation take up room in a Notes section. Proteins (talk) 15:50, 11 November 2008 (UTC)
I actually like the idea of the show/hide button. It is something an online encyclopedia can do but which a paper one cannot do, so it should be exploited! There are many cases when a casual reader would not want all the details of a proof/derivation, but someone really trying to understand the topic would want to read. MSGJ 17:45, 11 November 2008 (UTC)
- An online encyclopedia can also cause the text to blink, which cannot be done in print. — Carl (CBM · talk) 22:05, 11 November 2008 (UTC)
- Well that feature should definitely be implemented. Especially on all the "boring derivations" ;) MSGJ 14:18, 12 November 2008 (UTC)
- ...and also there are times when a reader adept in algebra (or whatever) would rather skip such routine steps, whereas to another reader they would not be routine. Michael Hardy (talk) 22:42, 11 November 2008 (UTC)
- I'll have a go at seeing if there isn't a way of ensuring the hidden text is shown if the user has disabled javascript. That's my chief objection to it currently. Probably is possible with a noscript tag surrounding some css but I won't have time today to check it. Lots of people disable javascript if at all possible as it cuts down a vector for viruses - and you know to what length some people interested in maths will follow logic. Dmcq (talk) 08:53, 13 November 2008 (UTC)
- I googled with 'noscript javascript css hide' and it came up with quite few instances of people dealing with this problem. It seems to rouse quite a bit of interest and people mention the accessibility problem if it isn't done. It looks like it would be worthwhile dealing with generally, and dealing with it isn't too difficult though requiring a little thought to avoid a problems. The main problem seems to be to that the obvious method of having the text visible and the javascript hiding it causes the page to flicker nastily whilst it is being rendered, it's better to use javascript in the head which links in a bit of css which hides the text. I haven't the foggiest how such a problem is fixed in wikipedia. Dmcq (talk) 21:53, 16 November 2008 (UTC)
Occurrence-in-subtuple problem
Occurrence-in-subtuple problem has been "prod"ed. Does anyone know anything about this? Michael Hardy (talk) 13:51, 15 November 2008 (UTC)
- I've removed the "prod" tag and done some editing. It is probably less obvious than it was that the person who wrote this is not a native speaker of English (e.g. I changed "what is regulated of it" to "what is regulated by it", and I made a number of analogous changes). But I'm wondering if this article has a counterpart in some other language and should be linked to it? The article still suffers from some deficiencies in the first author's understanding of how to write Misplaced Pages articles, and of how best to explain mathematics problems. Michael Hardy (talk) 14:08, 15 November 2008 (UTC)
Ultrafilter lemma vs. cardinality of bases
The vector space article currently says: "The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same "size", i.e. cardinality." Can somebody provide a reference for this, please? I didn't find one. Thanks, Jakob.scholbach (talk) 14:25, 15 November 2008 (UTC)
- "Bases in Vector Spaces and the Axiom of Choice", James D. Halpern, Proceedings of the American Mathematical Society, Vol. 17, No. 3 (Jun., 1966), pp. 670-673. JStor. — Carl (CBM · talk) 14:54, 15 November 2008 (UTC)
- The relevant passage in the article now reads:
- Every vector space has a basis. This fact relies on Zorn’s Lemma, an equivalent formulation of the axiom of choice. The ultrafilter lemma, which is weaker than the axiom of choice, implies that all bases of a given vector space have the same "size", i.e. cardinality. It is called the dimension of the vector space, denoted dim V. Given the other axioms of Zermelo-Fraenkel set theory, the latter statement is equivalent to the axiom of choice.
- It seems to me that the last sentence is inconsistent with the others. Perhaps someone inserted the sentence about ultrafilters and basis cardinalities after this latter (!) sentence was written? Plclark (talk) 20:50, 15 November 2008 (UTC)
- Yes, thanks for pointing it out, it was indeed a mis-restructuring of mine. It's fixed now. Jakob.scholbach (talk) 21:13, 15 November 2008 (UTC)
Number theory stub template
I also changed this template to the one User:Ben Tillman put instead of the previous algebra stub template. Again this is more representative of number theory (and that is why I changed it (I don't really think having the numbers 0,1 and 2 is useful although 1 and 0 may have some (slight) significance)). Hopefully there are no objections but if you have any, please post them and I can discuss.
Topology Expert (talk) 05:56, 16 November 2008 (UTC)
- The wording and formatting of stub templates is quite standardized; I don't think there's any reason to add a note "this template is not part of the article". If that note is needed because the image used might be misleading, then another image should be found. — Carl (CBM · talk) 11:42, 16 November 2008 (UTC)
\emptyset versus \varnothing
Does anyone else have an opinion on this?
The former, using \emptyset, looks like something that shows up because you're using an old-fashioned typewriter with a correspondingly limited character set, so you type the digit 0 and then backspace and type a slash over it. So I prefer the latter, using \varnothing. Michael Hardy (talk) 19:17, 16 November 2008 (UTC)
- I didn't even know \varnothing existed, but I like it better. Nice catch. Ryan Reich (talk) 19:26, 16 November 2008 (UTC)
- Same with me. Jakob.scholbach (talk) 19:49, 16 November 2008 (UTC)
- For the sake of semantics, I would say we should use \emptyset when talking about the empty set (it makes it easier for people reading the code, if nothing else). It should be possible to change the font so that it looks better, though, since \varnothing is certainly better. I don't know enough about LaTeX to know how one would do that (it will certainly require a request to the sysadmins, though). --Tango (talk) 19:52, 16 November 2008 (UTC)
- The fonts are what they are; mediawiki essentially just uses a vanilla LaTeX installation to compile the images. Knuth designed the emptyset symbol intentionally, which is why varnothing has the "var" prefix. — Carl (CBM · talk) 19:57, 16 November 2008 (UTC)
- I actually write , rather than , even in handwriting, and I always thought that was general practice. I am a model theorist, so pretty close to set theory, and in the rare instances when I see in print I always feel that that's an excentric choice.
- Just so that Michael Hardy's justification of his aesthetical decision doesn't remain unanswered, in my opinion is much worse because it tends to jump out of the text. For me it's analogous to printing every zero in bold. --Hans Adler (talk) 21:09, 16 November 2008 (UTC)
- Somehow I'm failing to see it jump out of the text any more than any other character either in mathematical notation or in plain-text sentences. Michael Hardy (talk) 22:57, 16 November 2008 (UTC)
- I was talking about printed articles or books. The symbols tends to be about two to three times as wide as what I consider the normal one, and is often not from the same font as many other mathematical symbols. --Hans Adler (talk) 23:38, 16 November 2008 (UTC)
- Somehow I'm failing to see it jump out of the text any more than any other character either in mathematical notation or in plain-text sentences. Michael Hardy (talk) 22:57, 16 November 2008 (UTC)
- I don't really like either of them that much, but between the two I prefer . To me looks like a 1950s-cartoon version of the planet Saturn. Or maybe just a generic planet. Which of course is a planet contained in all dense open sets of planets. --Trovatore (talk) 21:43, 16 November 2008 (UTC)
- Like Michael, Ryan, and Jakob, I prefer \varnothing too. But so what? Is it important? We generally follow the stylistic choices of the earliest principal editor. Geometry guy 21:56, 16 November 2008 (UTC)
- Heh. Let me demonstrate my ignorance, once again. I always assumed that \emptyset on TeX was some sort of font design mistake that was never fixed. Never occurred to me that someone might actually use that symbol in real life. linas (talk) 04:27, 17 November 2008 (UTC)
- That's how it's always seemed to me too. Michael Hardy (talk) 05:06, 18 November 2008 (UTC)
- Heh. Let me demonstrate my ignorance, once again. I always assumed that \emptyset on TeX was some sort of font design mistake that was never fixed. Never occurred to me that someone might actually use that symbol in real life. linas (talk) 04:27, 17 November 2008 (UTC)
- Like Michael, Ryan, and Jakob, I prefer \varnothing too. But so what? Is it important? We generally follow the stylistic choices of the earliest principal editor. Geometry guy 21:56, 16 November 2008 (UTC)
- The fonts are what they are; mediawiki essentially just uses a vanilla LaTeX installation to compile the images. Knuth designed the emptyset symbol intentionally, which is why varnothing has the "var" prefix. — Carl (CBM · talk) 19:57, 16 November 2008 (UTC)
Is there really no choice of font? When I make an \emptyset in pdflatex, on my own LaTeX installation, it comes out nicer than the one here. See this screenshot: ![]() . Aspect ratio seems to be about 3:2 (not counting the slash) whereas the WP one is more like 2:1, which seems too much. --Trovatore (talk) 07:01, 17 November 2008 (UTC)
. Aspect ratio seems to be about 3:2 (not counting the slash) whereas the WP one is more like 2:1, which seems too much. --Trovatore (talk) 07:01, 17 November 2008 (UTC)
- Hmm, OK, the difference isn't that extreme. I fiddled around a little, blowing up the images in Eye of Gnome and measuring them with KRuler and (while it's a bit subjective deciding where the "edge" is) it looks like the aspect ratio for the WP \emptyset is around 1.94 : 1, whereas the one that shows up on my LaTeX is about 1.83 : 1. Not a huge difference, but enough that the WP one does come out a bit scrawny, whereas I think the one that my setup gives is perfectly fine.
- Still, I like even the scrawny WP \emptyset better than \varnothing. --Trovatore (talk) 07:41, 17 November 2008 (UTC)
- Personally, I prefer JRSpriggs (talk) 16:57, 17 November 2008 (UTC)
- Seriously, or are you joking? That notation works alright stand-alone (though even there the fact that it's two glyphs instead of one is problematic), but as soon as you include it inside another set notated with curly braces, it gets confusing very quickly. --Trovatore (talk) 21:30, 17 November 2008 (UTC)
- Personally, I prefer JRSpriggs (talk) 16:57, 17 November 2008 (UTC)
\large character in math formatting
Is there a way of forcing a character to be bigger or smaller in tex on WP? I tried out \large and some options in \mbox but it complains about anything I do. I notice for \varnothing people were getting screen images to make it larger so I guess it's not possible, but my reading of tex says I should be able to do something like \mbox{\large 0} but I can't get anything along those lines to work. Dmcq (talk) 15:26, 17 November 2008 (UTC)
- There is some limited control of sizing possible by using \displaystyle, \textstyle, \scriptstyle, and \scriptscriptstyle. —David Eppstein (talk) 17:51, 17 November 2008 (UTC)
- They don't seem to be able to for instance double the size of a character. But they look very useful, the use in a continued fraction looked good. Dmcq (talk) 21:33, 17 November 2008 (UTC)
Overhaul of assessment and project banner
Looking at the assessment and categorisation of mathematics articles it seems to me that many improvements can be made and this WikiProject can be brought more into line with other projects. There could be several advantages to this.
- When new people join the project they are more likely to understand how things work if they have worked with other WikiProjects.
- As procedures evolve general in Misplaced Pages, there is less to do to keep our procedures up to date: by standardising, it is easier to keep individual projects up to date.
My main proposal is that we convert the project banner {{maths rating}} to use the standard meta-banner Template:WPBannerMeta. I have done quite a bit of work on this and the result is currently at Template:WikiProject Mathematics. It does not look exactly the same as the current one - I've got some examples to show you below. Other proposals are:
Other proposals
- Move categories Top/High/Mid/Low-Priority mathematics articles to Top/High/Mid/Low-Importance mathematics articles
Create categories on fields, i.e. Articles on Number theory/Discrete mathematics/Analysis/... with parent category Category:Mathematics articles by field.Struck because it would be duplication of categorisation of the article.- As B+ is not a standard class I suggest the following. Make B+ class articles a subset of B-Class articles (so B+ articles will appear in both categories)
- Clear out Category:WikiProject Mathematics articles so that it contains only subcategories. (Currently contains 145 pages and looks very cluttered.
- Move the assessment criteria which appears on every category (e.g. Category:WikiProject Mathematics articles) and link to it instead. (At the moment you have to scroll down a long to see the articles which are in the category.)
Questions
- Is it better to switch to the more standard Template:WikiProject Mathematics (and redirect Template:Maths rating to this) or stick to Template:Maths rating?
- Should we implement the full quality scale, which includes categories such as Featured List (a few of which do exist in the project) and disambiguation pages, or just the standard scale (FA, A, GA, B, Start, Stub, NA)?
- Currently Bplus-class articles are also categorised as GA-class. Have all these articles been listed as good articles? If yes, they should probably be classified as GA-class. If no, they should not be categorised as such.
Examples
Please see my sandbox for various different combinations. In order to show comments it was necessary to use mainspace, so I've pasted the proposed new banner on the following pages to demonstrate:
I will take personal responsibility to ensure that any changes work as desired and any teething problems are fixed. Your thoughts please? MSGJ 20:48, 17 November 2008 (UTC)
Discussion
- While the project in general makes some sense, I don't agree with changing Priority to Importance. The point is that these ratings are supposed to be a ranking of the priority assigned to improving the article, according to how it will affect the way users perceive the quality of the corpus of mathematical articles. Therefore more basic articles have higher priority; that makes sense to expert editors. You'll have a lot harder time convincing them that the basic subjects are more important than the shiny and sexy, but extremely specialized and technical, articles that they'd really prefer to work on. --Trovatore (talk) 21:11, 17 November 2008 (UTC)
- I take your point. But you could just think about it as being more important to work on particular articles at a particular time, rather than the actual subjects being more important than others. MSGJ 22:02, 17 November 2008 (UTC)
- Well, you could, but is that what people will do? Personally I would be offended to see a "low-importance" tag on pointclass -- it's an extraordinarily important topic. Just wouldn't go down my gullet, even with the explanation (and not everyone will know the explanation). But I can live with low-priority. I suppose.
- Frankly the better solution, if uniformity is desired here, would be to change it to "priority" everywhere else. This is a case where the math project has it right. --Trovatore (talk) 22:16, 17 November 2008 (UTC)
- I tend to agree with you in principle. I'm not sure if it's worth going against the overwhelming majority on this one. I notice that WikiProject Biography use "priority" and some other small projects like WikiProject British Royalty and Misplaced Pages:WikiProject Video games, but less than a dozen in total. MSGJ 09:46, 18 November 2008 (UTC)
- I take your point. But you could just think about it as being more important to work on particular articles at a particular time, rather than the actual subjects being more important than others. MSGJ 22:02, 17 November 2008 (UTC)
- Well, if it's a choice between following the majority on this or continuing to have our own convention, I say we go with our own convention. Uniformity has some value, but not that much. We can drop a hint in other projects' ear from time to time. --Trovatore (talk) 10:06, 18 November 2008 (UTC)
- It's funny that WikiProject Mathematics/Wikipedia 1.0/Assessment category format talks about importance more than priority. We also have Category:Mathematics articles by importance and Category:Unassessed importance mathematics articles. Seems we are confused! I have updated the banner to use the word priority instead of importance but we should decide which one we are going with. (And I still suggest we stick with the majority ...) MSGJ 12:04, 18 November 2008 (UTC)
- I thought that the categories were still named "by importance" because the WP 1.0 bot required it. However, I looked at the code and it looks like it should be fine with "by priority" instead. I never worried about it before because the categories are really only for the bot, so they can have strange names and only the bot operators need to worry about it. But I agree with Trovatore that "priority" is a more neutral term than "importance". The vast majority of our articles are Low-priority, but this in no way means they are of low importance. — Carl (CBM · talk) 13:19, 18 November 2008 (UTC)
- It's funny that WikiProject Mathematics/Wikipedia 1.0/Assessment category format talks about importance more than priority. We also have Category:Mathematics articles by importance and Category:Unassessed importance mathematics articles. Seems we are confused! I have updated the banner to use the word priority instead of importance but we should decide which one we are going with. (And I still suggest we stick with the majority ...) MSGJ 12:04, 18 November 2008 (UTC)
- Well, if it's a choice between following the majority on this or continuing to have our own convention, I say we go with our own convention. Uniformity has some value, but not that much. We can drop a hint in other projects' ear from time to time. --Trovatore (talk) 10:06, 18 November 2008 (UTC)
Well that's one thing that seems to be decided then (stick with Priority over Importance). Does anyone have any answers to my three questions? MSGJ 07:03, 19 November 2008 (UTC)
- 1. and 2. I personally don't feel the need to change anything there. 3: As far as I understand, the levels are more or less the same, but I think any article can be only either B+ or GA. The difference is that GA needs a review by somebody, whereas you can give B+ status yourself. Insofar I think it's good to have the two. Jakob.scholbach (talk) 10:01, 19 November 2008 (UTC)
Bplus class
The new template does not "categorize" Bplus articles as B articles – it completely replaces the Bplus class with B class. So there would be no more Bplus articles at all. In the past there has been support for keeping the Bplus rating. What do people thing now? — Carl (CBM · talk) 14:18, 20 November 2008 (UTC)
- This isn't true actually. The template is still populating Category:Bplus-Class mathematics articles. Bplus articles are now regarded as a subset of B-Class articles, so they will appear in both categories. We could make Category:Bplus-Class mathematics articles a subcategory of Category:B-Class mathematics articles articles to reflect this. MSGJ 14:22, 20 November 2008 (UTC)
- Traditionally Bplus articles have been treated as a subset of GA articles; this is more accurate in terms of quality.
- When the new WP 1.0 bot comes out (it's in development), it will explicitly support projects that have nonstandard ratings like this. So at that point the template will need to assign these articles to Bplus class and not at all to B class. I'm not sure how to achieve that with the new template; I don't think the NOTE_1 technique will work. I suppose at that point we can subst the WPBannerMeta template and fix the local copy. — Carl (CBM · talk) 15:58, 20 November 2008 (UTC)
- Or we could nominate all the Bplus articles for good articleship and do away with the Bplus class. MSGJ 16:31, 20 November 2008 (UTC)
- As I mentioned earlier, "good article" means a specific thing: articles which have been nominated and listed through the WP:Good articles process. I do not think it is appropriate to categorise articles as GA-Class when they are not good articles. MSGJ 17:11, 20 November 2008 (UTC)
- The only reason for the duplication at all is that the current WP 1.0 bot doesn't know how to handle Bplus. I agree this isn't ideal; that's why the next version of the WP 1.0 bot will handle the Bplus rating correctly. But the Bplus ones have been in the GA category for a long time, and I don't think there's a good reason to switch them to the B category. The table compiled by VeblenBot does give the correct numbers for Ga/Bplus/B, it's only the WP 1.0 bot table that is wrong. — Carl (CBM · talk) 17:44, 20 November 2008 (UTC)
- When the new WP 1.0 bot comes out (it's in development), it will explicitly support projects that have nonstandard ratings like this. So at that point the template will need to assign these articles to Bplus class and not at all to B class. I'm not sure how to achieve that with the new template; I don't think the NOTE_1 technique will work. I suppose at that point we can subst the WPBannerMeta template and fix the local copy. — Carl (CBM · talk) 15:58, 20 November 2008 (UTC)
Non-articles should not be assessed
Our longstanding consensus has been that the maths rating template is for rating math articles, not for tagging every page that is somehow related to math. Since the new banner template is quite willing to allow people to tag templates, categories, etc. with it, that's a problem. We could add a check to the template so that it only works on Talk: pages and not on other pages. It's really a pain to have to go back through and fix these after they have been mistakenly tagged by a well-intentioned editor (I know from experience). — Carl (CBM · talk) 14:20, 20 November 2008 (UTC)
- Question: by articles do you mean any page in main (article) space? Because there are various classes of articles which are in mainspace but are not counted as articles by the assessment scheme. For example, lists, featured lists, disambiguation pages, ... We should decide which of these we want to cater for and then not bother with the other categories. MSGJ 14:26, 20 November 2008 (UTC)
- Well, maybe this stand point should be re-evaluated. There are good reason for tagging non-article pages with project banners. For example it makes it a lot easier to contact the interested wikiprojects when a page is subject of discussion, for example when it is proposed for deletion.
- Also, I see very little reason not to do it. (Other than it is a lot of work to add the banners, but that is a none problem, since in the end somebody will come around and do it.) (TimothyRias (talk) 14:39, 20 November 2008 (UTC))
- We also have quite a few mathematical pictures, and it might well be useful to have these in a category together, e.g. Image-Clas Mathematics articles. MSGJ 15:24, 20 November 2008 (UTC)
- We already have a category for them: Category:Mathematics images. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- We also have quite a few mathematical pictures, and it might well be useful to have these in a category together, e.g. Image-Clas Mathematics articles. MSGJ 15:24, 20 November 2008 (UTC)
- Timothy: which pages are you talking about, that this project might need to be notified of their deletion? Apart from a few templates and the subpages of WP:WPM, I can't see how we'd be very interested in announcements about non-articles. It's just not a very common problem. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- The various mathematics templates would definitely be an example. So, are the mathematics categories and images etc. (As note to the side, WPBannerMeta also supports an option to only allow the old restricted range of classes. (TimothyRias (talk) 16:19, 20 November 2008 (UTC))
- It's extremely rare for any of these to be put up for deletion, in practice. I don't think that justifies the effort of tagging them just for the 1 in a million chance it might someday be useful. — Carl (CBM · talk) 16:39, 20 November 2008 (UTC)
- As a general point: we already have List of mathematics articles that includes lists, featured lists, articles, etc. and does not require any talk page tags at all. It's based just on the categorization of the pages themselves. So the only added benefit of talk page tags is for article assessments. — Carl (CBM · talk) 16:06, 20 November 2008 (UTC)
- Well, actually there is also the advantage of easier maintenance. If categories are applied through a template, it is much easier to later adjust the categories, or for example create cross-category lists. I do admit that this benefits mainspace articles much more than the other articles.(TimothyRias (talk) 16:19, 20 November 2008 (UTC))
- I don't follow. In the ordinary course of editing, categories are added to the article itself, which causes the article to appear in the List of mathematics articles. No extra maintenance or effort is required, and the talk page doesn't even have to be created. — Carl (CBM · talk) 16:39, 20 November 2008 (UTC)
Preamble to categories by quality/importance
Regarding proposal 5 above, it seemed to me that these categories had too much information on them and were very cluttered. You needed to scroll down a long way to actually see what articles were in those categories. My proposal is to have some brief information about assessing articles and a link to a page with the full details. The more standard method is just a simple template at the top which links to the other categories (see this
- There's not a lot of reason to manually browse the category lists; there are nicely formatted lists such as
- for human consumption.
- There may have been too much text on the old template, but the general strategy of using a single template is sound. It keeps the pages in sync and makes it easier to change them all with one edit when needed. — Carl (CBM · talk) 16:01, 20 November 2008 (UTC)
What happened to the "field" parameter?
The new template doesn't seem to do anything with the "field" parameter. Is this a bug? --Trovatore (talk) 22:11, 20 November 2008 (UTC)
"Occurrence-in-subtuple problem" on AfD
Occurrence-in-subtuple problem, an article about a combinatorial problem said to have applications in genetics, has been nominated for deletion. It is obvious that the reason for some of the imperfections in writing is that it was written by someone who is not a native speaker of English. That of course is a reason to clean it up, not to delete it. The substantial objection seems to be an allegation of original research, concerning which I have no settled opinion. Michael Hardy (talk) 05:11, 18 November 2008 (UTC)
Hilbert's thirteenth problem
Can someone provide precise statements of the theorems of Kolmogorov and Arnold that are mentioned in a hand-waving way in Hilbert's thirteenth problem? Some sources on the web speak of "superposition", which I usually think of as meaning addition, but some other speak of "composition", which I usually think of as something quite different from addition. The Misplaced Pages article ought to give a precise statement of the problem if possible. Michael Hardy (talk) 06:11, 18 November 2008 (UTC)
Current good article nominations
I have nominated the vector space article for WP:Good article nomination#Mathematics. I'd be thankful if people around could have a look, particularly those knowledgeable in analysis. Jakob.scholbach (talk) 09:28, 18 November 2008 (UTC)
P.S. There are two other current nominations (nominated by other editors), Mayer-Vietoris sequence and Robert Hues. I'd like to encourage people to review articles. It's fun, usually pretty interesting and helps the author of the article a lot. Thanks, Jakob.scholbach (talk) 09:36, 18 November 2008 (UTC)
- I just spotted something wrong in "Banach spaces" section of "Vector space" (see the discussion page). Boris Tsirelson (talk) 07:53, 19 November 2008 (UTC)
- Can't it be a featured article (haven't read it yet but I will do so now)?
Topology Expert (talk) 07:54, 19 November 2008 (UTC)
- Well -- "can't" is a bit the wrong question ;). It needs somebody to work on it further, push it through the pretty tedious FAC and so on. I haven't decided yet whether I'm up to it. The question is a little bit: an additional (estimated) 5% of article quality needs an additional 50% of work. Spending this time on other articles that are not yet so well-developed may be more fruitful. One thing I can recommend to everybody, though: take a maths-rating category, and take the top-priority class articles in there. Pick one article and move it (by editing it appropriately) two steps up, e.g. from Start to B+ etc. I'm focussing on algebra-top-priority at the moment. Jakob.scholbach (talk) 19:48, 19 November 2008 (UTC)
Logical connective
A single-purpose account User:Boolean hexadecimal, proposes replacing a large amount of text in tables with a large imagemap (so that the text is replace by an image of text). The image is not only less clear than the tables, it's awful for accessibility. Could someone else look into this? — Carl (CBM · talk) 20:56, 18 November 2008 (UTC)
- It looks like he did that to the German equivalents is trying to update the English version to the same, his German account is de:Benutzer:Boolean hexadecimal. I think it's probably just a question of somebody pointing out the problems and saying the information needs to be accessible.
- As a matter of interest on accessibility - how would a blind person get access to the formulae displayed using <math> on WP, is there something about that somewhere? Dmcq (talk) 10:47, 19 November 2008 (UTC)
- This isn't the first time he's done this. Although I remember his gigantic imagemap being orange instead of blue. —Dominus 14:21, 19 November 2008 (UTC)
- Here. —Dominus 14:23, 19 November 2008 (UTC)
- I had a good look at it and decided even if it was good I would be against it. The reason is that it would lock out other editors. We should try as far as possible I feel make contributions such that someone good at the subject can contribute - not have people versed in html make things difficult for them. Dmcq (talk) 19:58, 19 November 2008 (UTC)
- Here. —Dominus 14:23, 19 November 2008 (UTC)
Strange software bug?
First:
- \frac{z}{e^z-1}=\sum_{n=0}^\infty \frac{B_n}{n!} z^n
Second:
- \frac{z}{e^z-1}=\sum_{n=0}^\infty \frac{B_n}{n!} {z^n}
First, within "math" tags:
Second, within "math" tags:
At radius of convergence, this first form was failing to get rendered. Why? Michael Hardy (talk) 23:30, 18 November 2008 (UTC)
- No-one's sure why, AFAIK. For some reason, the server generates a corrupt image for the first code, and this image has to be manually deleted by someone with server access to allow the server to generate a non-broken image. Because the second code is different, the server doesn't use the (broken) cached image but generates a new one instead. Algebraist 23:38, 18 November 2008 (UTC)
- Just add "?action=purge" to the URL and the cache (on the server) is purged. I did that. Now all you have to do is purge your own cache by typing control-shift-R. Voila, it is fixed! JRSpriggs (talk) 09:23, 19 November 2008 (UTC)
- Where "the URL" is the URL of the page that contains the broken image? Or some other URL? Cheers, Ben (talk) 09:37, 19 November 2008 (UTC)
- Just add "?action=purge" to the URL and the cache (on the server) is purged. I did that. Now all you have to do is purge your own cache by typing control-shift-R. Voila, it is fixed! JRSpriggs (talk) 09:23, 19 November 2008 (UTC)
The problem seems to have been fixed. I edited the article and it looks good now. Michael Hardy (talk) 18:14, 19 November 2008 (UTC)
- The URL is the URL of any page or section which contains the problematic image. Once you do the purge on one of them, the image is re-computed and re-cached for all of them, I think. JRSpriggs (talk) 17:58, 20 November 2008 (UTC)
DYK participation
DYK has started keeping track of which article have received the most page views while being featured on the Main Page. See Misplaced Pages:DYKBEST. DYK would like to make its section of the Main Page more effective. We are in need of Wikipedians who can review the raw Misplaced Pages:DYKBEST data and come up with factors that make it more likely that an article will receive page views. If interested, please feel free to review the data and edit Misplaced Pages:DYKBEST#Features_of_an_effective_DYK_hook. Thanks. -- Suntag ☼ 08:22, 20 November 2008 (UTC)
Peer review for Locally connected space
Anyone who is interested is welcome to contribute. Any comments/feedback (however minor) will be greatly appreciated.
Thanks, Topology Expert (talk) 11:12, 20 November 2008 (UTC)
Geometry stub template
Don't fear the heading; wait till the end of my message. A non-mathematician keeps reverting my changes to this but I found a perfect image. To make this discussion short, have a look at this. Then type either 1 (for agree with my image) or 0 (if you disagree). No explanations required. If my image is not favourable (after 5-7 people vote), I will immediately revert my inclusion of that image. Please decide on the basis of the image rather than the previous discussion and also note that my image represents the connected sum (differential geometry). Anyone can understand that the image illustrates two objects being glued together and furthermore, this is more representative than a dodecahedron.
Topology Expert (talk) 11:49, 20 November 2008 (UTC)
If necessary, the image size can be increased by a few pixels and this should make it more clearer.
Topology Expert (talk) 11:51, 20 November 2008 (UTC)
- Oh dear TE. Comments like:
- aren't going to win you any arguments. Misplaced Pages isn't mathematicians vs. the world. It's a community project that anyone is allowed to join and make contributions to. Various policies should, and do, dictate what stays, goes and changes, not a persons qualifications. Can I recommend you leave the stub templates alone for a while? Ben (talk) 12:18, 20 November 2008 (UTC)
- 0, sorry. MSGJ 12:12, 20 November 2008 (UTC)
- 0, too Jakob.scholbach (talk) 12:16, 20 November 2008 (UTC)
- 0. Ben (talk) 12:18, 20 November 2008 (UTC)
- 0 (note also that connected sum is a topological notion more than a geometrical one.) (TimothyRias (talk) 12:39, 20 November 2008 (UTC))
- 0. The idea of the image is invisible without a microscope. Michael Hardy (talk) 14:21, 20 November 2008 (UTC)
Ok (you don't have to say sorry by the way). First of all, I had a dispute with User:Moondyne regarding something else and he threatened to block me. Next, he started tracing my edits and reverting them (these edits were mathematics-based). I didn't mean to be rude, but I am trying to expand Misplaced Pages. If users threaten to block me, be rude (User:Moondyne), don't agree with me (I think users are against me now but I can't do anything about it) and undo my edits, then it seems that it would be best if I retire. And I know that no one really would care if I retired (I have better things to do anyhow (as everyone here does)). I also don't see why User:Ben Tillman had to bring something irrelevant into this discussion.
I have to keep my promise, but the image I put up is representative of geometry (differential geometry in fact and also has very important applications in fibre bundle theory), small and clear, easy to understand, and probably the same as the previous image except for the fact that they represent different topics. What is the problem (you don't have to answer this and if no-one does I might as well revert my inclusion of that image)?
Topology Expert (talk) 12:48, 20 November 2008 (UTC)
By the way, there was an edit conflict and I just wanted to note that the connected sum belongs to differential geometry.
Topology Expert (talk) 12:48, 20 November 2008 (UTC)
- The connected sum image is invisible. You need a microscope to see it. I clicked on the image in the template and saw the larger picture and only then could I tell what it was. Michael Hardy (talk) 14:19, 20 November 2008 (UTC)
Please note also that many of the articles in {{geometry-stub}} are about things Euclid would recognize as geometry, which may be very different from the things a modern mathematics department's hiring committee would recognize as geometry. —David Eppstein (talk) 15:32, 20 November 2008 (UTC)
- This discussion fits in with the one about the difference between priority and importance in the article ratings. A nice picture of a dodecahedron like there was before probably would have greater priority. Dmcq (talk) 15:43, 20 November 2008 (UTC)
You may as well revert then. I thought it was quite visible but that's my opinion. Anyway, Euclid was 2000 years ago, as far as I know no-one works in Euclidean geometry any longer.
But now that I look at it, maybe I will vote 0 as well.
Topology Expert (talk) 23:44, 20 November 2008 (UTC)
- While we're holding votes, here's another: is Topology Expert a troll or just an insufferable snob? WP:AGF would argue for the latter, I suppose, but it seems shocking to me that I would have to defend Euclidean geometry as a subject of interest here, or for that matter as a subject of research, despite its unpopularity among more-serious-than-thou mathematicians. —David Eppstein (talk) 01:10, 21 November 2008 (UTC)
- 0 I'm afraid to say. These images are simply icons, with a vanishingly small information content. They lie more in the realm of graphic design than mathematics, attempting to convey to much information in a small space is doomed. I see no compelling reason why we need an image at all. The wording This geometry-related article is a stub. You can help Misplaced Pages by expanding it conveys all the essential information, any icon just serves as visual clutter. To be awkward I've removed the image entirely. Does this do the job? --Salix (talk): 00:09, 21 November 2008 (UTC)
- I don't think removing the images is a good idea. The problem is that without an image, it's not instantly obvious that the wording of the template isn't part of the article. Also the images serve a useful function by making the stub types easily distinguishable from one another. --Trovatore (talk) 01:02, 21 November 2008 (UTC)



 ?
?  and other silliness. What you are arguing is the philosophical complement of what you started out denouncing: first the tag was oversimplified to the point of being misleadingly trivial; you now explicitly advocate it being overgeneralized to the point of being obscuringly deep.
and other silliness. What you are arguing is the philosophical complement of what you started out denouncing: first the tag was oversimplified to the point of being misleadingly trivial; you now explicitly advocate it being overgeneralized to the point of being obscuringly deep.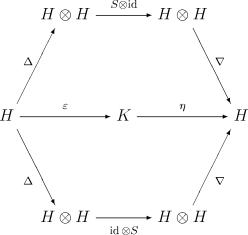
 is boring? When I first learnt about these infinite cardinalities, I was fascinated (and excited to prove by myself that
is boring? When I first learnt about these infinite cardinalities, I was fascinated (and excited to prove by myself that  ).
).

 represents the integers and practically everyone has a vague idea as to what the arrows are (a function). This would be more exciting as an image, more concise, and much better than a dinosaur commutative diagram. Any opinions on whether or not this would be preferable to a commutative diagram?
represents the integers and practically everyone has a vague idea as to what the arrows are (a function). This would be more exciting as an image, more concise, and much better than a dinosaur commutative diagram. Any opinions on whether or not this would be preferable to a commutative diagram?

 into {{
into {{ . This includes both associative and nonassociative operations.
. This includes both associative and nonassociative operations. 
 . Then the whole section in question can be omitted.
. Then the whole section in question can be omitted.  . But 'scuse me for trying to help you with a suggestion - next time I won't bother.
. But 'scuse me for trying to help you with a suggestion - next time I won't bother. 



 , rather than
, rather than  , even in handwriting, and I always thought that was general practice. I am a model theorist, so pretty close to set theory, and in the rare instances when I see
, even in handwriting, and I always thought that was general practice. I am a model theorist, so pretty close to set theory, and in the rare instances when I see 

