| Revision as of 20:00, 25 September 2006 editByrgenwulf (talk | contribs)1,234 editsNo edit summary← Previous edit | Revision as of 20:42, 25 September 2006 edit undoAnville (talk | contribs)6,887 editsm copy edits in leadNext edit → | ||
| Line 1: | Line 1: | ||
| '''Relational quantum mechanics''' ('''RQM''') is an ] treats the state of a quantum system as being observer-dependent, i.e. the relation between the observer and the system. Inspired by the key idea behind ], that the details of an ] depend on the ] of the observer, and making use of some ideas from ] on ]<ref>Wheeler, 1990: pg. 3</ref>, this interpretation was first delineated by ] in a ] ], and has since been expanded upon by a number of theorists. | '''Relational quantum mechanics''' ('''RQM''') is an ] which treats the state of a quantum system as being observer-dependent, ''i.e.,'' dependent upon the relation between the observer and the system. Inspired by the key idea behind ], that the details of an ] depend on the ] of the observer, and making use of some ideas from ] on ]<ref>Wheeler, 1990: pg. 3</ref>, this interpretation was first delineated by ] in a ] ], and has since been expanded upon by a number of theorists. | ||
| The essential idea behind RQM is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" ], while to another observer at the same time, it may be in a ] of two or more states. Consequently, if quantum mechanics is to be a ] theory, RQM argues that the notion of "state" describes not the observed system itself, but the relationship, or ], between the system and its observer(s). The ] of conventional quantum mechanics becomes a description of the correlation of some '']'' in the observer, with respect to the observed system. However, it is held by RQM that this applies to all physical objects, whether or not they are ] or ] (all systems are quantum systems). Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory is to do not with objects themselves, but the relations between them. | The essential idea behind RQM is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" ], while to another observer at the same time, it may be in a ] of two or more states. Consequently, if quantum mechanics is to be a ] theory, RQM argues that the notion of "state" describes not the observed system itself, but the relationship, or ], between the system and its observer(s). The ] of conventional quantum mechanics becomes a description of the correlation of some '']'' in the observer, with respect to the observed system. However, it is held by RQM that this applies to all physical objects, whether or not they are ] or ] (all systems are quantum systems). Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory is to do not with objects themselves, but the relations between them. | ||
Revision as of 20:42, 25 September 2006
Relational quantum mechanics (RQM) is an interpretation of quantum mechanics which treats the state of a quantum system as being observer-dependent, i.e., dependent upon the relation between the observer and the system. Inspired by the key idea behind Special Relativity, that the details of an observation depend on the reference frame of the observer, and making use of some ideas from Wheeler on quantum information, this interpretation was first delineated by Carlo Rovelli in a 1994 preprint, and has since been expanded upon by a number of theorists.
The essential idea behind RQM is that different observers may give different accounts of the same series of events: for example, to one observer at a given point in time, a system may be in a single, "collapsed" eigenstate, while to another observer at the same time, it may be in a superposition of two or more states. Consequently, if quantum mechanics is to be a complete theory, RQM argues that the notion of "state" describes not the observed system itself, but the relationship, or correlation, between the system and its observer(s). The state vector of conventional quantum mechanics becomes a description of the correlation of some degrees of freedom in the observer, with respect to the observed system. However, it is held by RQM that this applies to all physical objects, whether or not they are conscious or macroscopic (all systems are quantum systems). Any "measurement event" is seen simply as an ordinary physical interaction, an establishment of the sort of correlation discussed above. Thus the physical content of the theory is to do not with objects themselves, but the relations between them.
Sections 1 to 5 of this article describe the history and interpretation of the idea and analyse its logical and philosophical nature, while the last two sections describe the formal background to the theory and the mathematics of its construction, as well as provide an analysis of its application to the EPR paradox.
History and development
Relational Quantum Mechanics arose from a historical comparison of the quandaries posed by the interpretation of quantum mechanics with the situation after the Lorentz transformations were formulated but before Special Relativity. Rovelli felt that just as there was an "incorrect assumption" underlying the pre-relativistic interpretation of Lorentz's equations, which was corrected by Einstein's derivation of them from Lorentz covariance and the constancy of the speed of light in all reference frames, so a similarly incorrect assumption underlies many attempts to make sense of the quantum formalism. This incorrect assumption, he said, was that of an observer-independent state of a system, and he laid out the foundations of this interpretation to try to overcome the difficulty. Since then, the idea has been expanded upon by Lee Smolin and Louis Crane, who have both applied the concept to quantum cosmology, and Rovelli has also developed the idea further, particularly in applying it to the EPR paradox and Bell's Theorem in collaboration with Matt Smerlak.
The problem of the "observer observed"
This problem was initially discussed in detail in Everett's thesis, The Theory of the Universal Wavefunction. Consider the diagram to the right. Observer measures the state of the quantum system (represented by a Feynman diagram). We assume that he has complete information on the system, and that he can write down the wavefunction describing this particle. At the same time, there is another observer , who is interested in the state of the entire Feynman diagram-physicist-experiment system, and that he likewise has complete information.
To analyse this system formally, we consider a system which may take one of two states, which we shall designate and , ket vectors in the Hilbert space . Now, the observer wishes to make a measurement on the system. At time , this observer may characterize the system as follows:
where and are probabilities of finding the system in the respective states, and obviously add up to 1. For our purposes here, we can assume that in a single experiment, the outcome is the eigenstate (but this can be substituted throughout, mutatis mutandis, by ). So, we may represent the sequence of event in this experiment, with observer doing the observing, as follows:
This is observer 's description of the measurement event. Now, any measurement is also a physical interaction between two or more systems. Accordingly, we can consider the tensor product Hilbert space , where is the Hilbert space inhabited by state vectors describing . If the initial state of is , after the measurement, some degrees of freedom in become correlated with the state of , and this correlation can take one of two values: or where the direction of the arrows in the subscripts corresponds to the outcome of the measurement that has made on . If we now consider the description of the measurement event by the other observer, , who describes the combined system, but does not interact with it, the following gives the description of the measurement event according to , from the linearity inherent in the quantum formalism:
Thus, on the assumption (see hypothesis 2 above) that quantum mechanics is complete, the two observers and give different but equally correct accounts of the events . In particular, may be interested in ascertaining whether or not the state of accurately reflects the state of . We can draw up for an operator, , which is specified as:
with an eigenvalue of 1 meaning that indeed accurately reflects the state of . So there is a 0 probability of reflecting the state of as being if it is in fact ,and so forth. The implication of this is that at time , can predict with certainty that the system is in some eigenstate of , but cannot say which eigenstate it is in, unless itself interacts with the system. knows that there is a correlation, but cannot describe the correlation without interaction, and hence breaking the unitary evolution of the compound system.
Central principles
Observer-dependence of state
The standard mathematical formulation of quantum mechanics allows different observers to give different accounts of the same sequence of events (see the "problem of the observer observed" above for a formal description of how this works). There are many ways to overcome this perceived difficulty. It could be described as an epistemic limitation - observers with a full knowledge of the system, we might say, could give a complete and equivalent description of the state of affairs, but that obtaining this knowledge is impossible in practice. Alternatively, we could claim that quantum mechanics is not a complete theory, and that by adding more structure we could arrive at a universal descripion. Yet another option is to give a preferred status to a particular observer or type of observer, and assign the epithet of "correctness" to their description alone.
RQM, however, takes the point illustrated by the Third Man problem at face value. As Rovelli puts it "my effort here is not to modify quantum mechanics to make it consistent with my view of the world, but to modify my view of the world to make it consistent with quantum mechanics" . "State" is an observer-dependent property, just like simultaneity in Special Relativity. This insight follows logically from the two main hypotheses which inform this interpretation:
- Hypothesis 1: the equivalence of systems. There is no a priori distinction that should be drawn between "quantum" and "macroscopic" systems. All systems are, fundamentally, quantum systems.
- Hypothesis 2: the completeness of quantum mechanics. There are no hidden variables or other factors which may be appropriately added to quantum mechanics, in light of current experimental evidence.
Thus, if state is to be observer-dependent, then a description of a system would follow the form "system S is in state x with reference to observer O" or similar constructions, much like in relativity theory. There is no meaning in RQM in the "absolute", observer-independent state of any system.
Information and correlation
It is generally well established that any quantum mechanical measurement can be reduced to a set of yes/no questions. RQM makes use of this fact to formulate the state of a quantum system (relative to a given observer!) in terms of the physical notion of information developed by Claude Shannon. Any yes/no question can be described as a single bit of information. This should not be confused with the idea of a qubit from quantum information theory, because a qubit can be in a superposition of values, whilst the "questions" of RQM are ordinary binary variables.
Any quantum measurement is fundamentally a physical interaction between the system being measured and some form of measuring apparatus. By extension, any physical interaction may be seen to be a form of quantum measurement, as all systems are seen as quantum systems in RQM. A physical interaction is seen as establishing a correlation between the system and the observer, and this correlation is what is described and predicted by the quantum formalism.
But, this form of correlation is, Rovelli points out, precisely the same as the definition of information in Shannon's theory. Specifically, an observer O observing a system S will, after measurement, have some degrees of freedom correlated with those of S, and the amount of this correlation is given by log2k bits, where k is the number of possible values which this correlation may take - the number of "options", or permutations, there are.
A key advantage of thus construing the notion of state is that physical information, in the Shannon sense, does not require consciousness, macroscopic objects, deliberate measurement or any condition other than the two systems interact in some way (which may, upon extension, include such interactions as the exchange of a virtual particle or similar effects).
Implications
Self-reference
Because "state" is expressed in RQM as the correlation between two systems, there can be no meaning to "self-measurement". If observer O measures system S, S's "state" is represented as correlation between O and S. O itself cannot say anything with respect to its own "state", because its own "state" is defined only relative to another observer, O'. If the S+O compound system does not interact with any other systems, then it will possess a clearly defined state relative to O'. However, because O's measurement of S breaks its unitary evolution with respect to O, O will not be able to give a full description of the S+O system (since it can only speak of the correlation between S and itself, not its own behaviour). A complete description of the (S+O)+O' system can only be given by a further, external observer, and so forth.
Relational networks
An interesting implication of RQM arises when we consider that interactions between material systems can only occur within the constraints prescribed by Special Relativity, namely within the intersections of the light cones of the systems: when they are spatiotemporally contiguous, in other words. Relativity tells us that objects have location only relative to other objects. On the assumption that all interactions are local (which is backed up by the analysis of the EPR paradox presented below), one could say that the ideas of "state" and spatiotemporal contiguity are two sides of the same coin: spacetime location determines the possibility of interaction, but interactions determine spatiotemporal structure. By extension, a network of relations could be built up based on the properties of a set of systems, which determines which systems have properties relative to which others, and when (since properties are no longer well defined relative to a specific observer after unitary evolution breaks down for that observer). Some, such as Cifone et al. in their evalution of a "relational blockworld" , have gone so far as to describe these intersections as determinants of "reality", with objects possessing well-defined properties relative to one another being "co-real". At any rate, the manner in which the spacetime structure is built up by networks of interaction and vice versa is, while at this stage still vague, nonetheless an intriguing allusion.
RQM and quantum cosmology
It is a sound observation, from both a philosophical and physical perspective, that one should avoid evaluating cosmological scenarios in terms of an observer (whether "real" or "imaginary") outside of the system - which in this case, of course, is the universe. Philosophically, this is because the universe is the sum total of all that is in existence. Physically, a (physical) observer outside of the universe would require the breaking of gauge invariance, and a concomitant alteration in the mathematical structure of the theory. Similarly, RQM conceptually forbids the possibility of an external observer. Since the assignment of a quantum state requires at least two "objects" (system and observer), which must both be physical systems, there is no meaning in speaking of the "state" of the entire universe, because this state would have to be ascribed to a correlation between the universe and some other physical observer, but this observer in turn would have to form part of the universe, and as was discussed above, it is impossible for an object to give a complete specification of itself. Following the idea of relational networks above, an RQM-oriented cosmology would have to account for the universe as a set of partial systems providing descriptions of one another. The exact nature of such a construction remains an open question.
Ontology and epistemology
The philosophical implications of RQM are far-reaching. Perhaps foremost among them is the nominalism implied by the absence of the observer-independent state of a system. A state, after all, is nothing but a compound of properties that a system possesses, and RQM implies that properties of a system are better ascribed to the relationship between the system and a particular observer. Thus properties do not inhere in the objects themselves, and exist as binary relations between objects, not unary relations as is the more typical view.
If some form of epistemological naturalism is granted, meaning that epistemic propositions are merely indicators of correlation of state between an individual and their environment, a form of coherentism is implied by RQM. One of the key results of the theory is that despite the lack of an "absolute, underlying state", two or more individuals reporting on their observations will agree as to what they have observed (see the ""-operator below).
Relationship with other interpretations
The only group of interpretations of quantum mechanics with which RQM is almost completely incompatible is that of hidden variables theories. RQM shares some deep similarities with other views, but differs from them all to the extent to which the other interpretations do not accord with the "relational world" put forward by RQM.
Copenhagen interpretation
RQM is, in essence, quite similar to the Copenhagen interpretation (CI), but with an important difference. In the Copenhagen interpretation, the world is assumed to be intrinsically classical in nature, and wave collapse occurs when a quantum system interacts with macroscopic apparatus. In RQM, any interaction, be it micro- or macroscopic, causes the linearity of Schrödinger evolution to break down. RQM could "recover" a Copenhagen-like view of the world by assigning a "privileged" status (not dissimilar to a preferred frame in relativity) to the classical world. However, by doing this one would lose sight of the key features that RQM brings to our view of the quantum world.
Hidden variables theories
Bohm's interpretation of QM does not sit well with RQM. One of the explicit hypotheses in the construction of RQM is that quantum mechanics is a complete theory, i.e. it provides a full account of the world. Moreover, the Bohmian view seems to imply an underlying, "absolute" set of states of all systems, which is also ruled out as a consequence of RQM.
We find a similar incompatibility between RQM and suggestions such as that of Penrose, which postulate that some process (in Penrose's case, gravitational effects) violate the linear evolution of the Schrödinger equation for the system.
Relative-state formulation
The many-worlds family of interpretations (MWI) shares an important feature with RQM, namely a relational view of the world. However, there is a tendency in some instances of this interpretation to overlook Everett's insight in this regard, which may give rise to problems similar to that of when wave collapse occurs: when does "branching" of the wavefunction happen?
However, many proponents of the MWI do insist on a purely relational interpretation, by maintaining the relational nature of all value assignments (i.e. properties). RQM and MWI are very similar, then, except for one thing. Everett's universal wavefunction is held to give a description of the entire universe. Rovelli argues that this is problematic, not only because it provides a description which is not tied to a specific observer (which is a meaningless description in RQM); in RQM, there is no one, absolute description of the universal as a whole, but rather a net of inter-related partial descriptions.
Consistent histories approach
In the consistent histories approach to QM, instead of assigning probabilities to single values for a given system, the emphasis is given to sequences of values, in such a way as to exclude (as physically impossible) all value assignments which result in inconsistent probabilities being attributed to observed states of the system. This is done by means of ascribing values to "frameworks", and all values are hence framework-dependent.
RQM accords perfectly well with this view. However, where the consistent histories approach does not give a full description of the physical meaning of framework-dependent value (i.e. it does not account for how there can be "facts" if the value of any property depends on the framework chosen), by incorporating the relational view into this approach, the problem is solved: RQM provides the means by which the observer-independent, framework-dependent probabilities of various histories are reconciled with observer-dependent descriptions of the world.
EPR and quantum non-locality
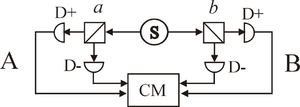
The source S produces pairs of "photons", sent in opposite directions. Each photon encounters a two-channel polariser whose orientation can be set by the experimenter. Emerging signals from each channel are detected and coincidences counted by the coincidence monitor CM.
RQM provides an unusual solution to the EPR paradox. Indeed, it manages to dissolve the problem altogether, inasmuch as there is no superluminal transportation of information involved in a Bell test experiment.
Derivation
RQM offers the possibility of being derived from a small number of axioms, or postulates based on experimental observations. Rovelli's derivation of RQM uses three fundamental postulates. However, it has been suggested that it may be possible to reformulate the third postulate into a weaker statement, or possibly even do away with it altogether. The derivation of RQM parallels, to a large extent, quantum logic. The first two postulates are motivated entirely by experimental results, while the third postulate, although it accords perfectly with what we have discovered experimentally, is introduced as a means of recovering the full Hilbert space formalism of quantum mechanics from the other two postulates. The 2 empirical postulates are:
- Postulate 1: there is a maximum amount of relevant information that may be obtained from a quantum system.
- Postulate 2: it is always possible to obtain new information from a system.
We let denote the set of all possible questions that may be "asked" of a quantum system, which we shall denote by , . We may experimentally find certain relations between these questions: , corresponding to {intersection, orthogonal sum, orthogonal complement, inclusion, and orthogonality} respectively, where .
From the first postulate, it follows that we may choose a subset of mutually independent questions, where is the number of bits contained in the maximum amount of information. We call such a question a complete question. The value of can be expressed as an N-tuple sequence of binary valued numerals, which has possible permutations of "0" and "1" values. There will also be more than one possible complete question. If we further assume that the relations are defined for all , then is an orthomodular lattice, while all the possible unions of sets of complete questions form a Boolean algebra with the as atoms.
The second postulate governs the event of further questions being asked by an observer of a system , when already has a full complement of information on the system (an answer to a complete question). We denote by the probability that a "yes" answer to a question will follow the complete question . If is independent of , then , or it might be fully determined by , in which case . There is also a range of intermediate possibilities, and this case is examined below.
If the question that wants to ask the system is another complete question, , the probability of a "yes" answer has certain constraints upon it:
The three constraints above are inspired by the most basic of properties of probabilities, and are satisfied if
- ,
where is a unitary matrix.
- Postulate 3 If and are two complete questions, then the unitary matrix associated with their probability described above satisfies the equality , for all and .
This third postulate implies that if we set a complete question as a basis vector in a complex Hilbert space, we may then represent any other question as a linear combination:
And the conventional probability rule of quantum mechanics states that if two sets of basis vectors are in the relation above, then the probability is
Dynamics
The Heisenberg picture of time evolution accords most easily with RQM. Questions may be labelled by a time parameter , and are regarded as distinct if they are specified by the same operator but are performed at different times. Because time evolution is a symmetry in the theory (it forms a necessary part of the full formal derivation of the theory from the postulates), the set of all possible questions at time is isomorphic to the set of all possible questions at time . It follows, by standard arguments in quantum logic, from the derivation above that the orthomodular lattice has the structure of the set of linear subspaces of a Hilbert space, with the relations between the questions corresponding to the relations between linear subspaces.
It follows that there must be a unitary transformation that satisfies:
- , and
where is the Hamiltonian, a self-adjoint operator on the Hilbert space and the unitary matrices are an abelian group.
See also
- Interpretation of quantum mechanics
- Many-worlds interpretation
- Quantum information
- Philosophy of physics
References
- Crane, L.: "Clock and Category: Is Quantum Gravity Algebraic?"; Journal of Mathematical Physics 36; 1993: 6180-6193; arXiv:gr-qc/9504038.
- Everett, H.: "The Theory of the Universal Wavefunction"; Princeton University Doctoral Dissertation; in DeWitt, B.S. & Graham, R.N. (eds.): "The Many-Worlds Interpretation of Quantum Mechanics"; Princeton University Press; 1973.
- Laudisa, F. & Rovelli, C.: "Relational Quantum Mechanics"; The Stanford Encyclopedia of Philosophy (Fall 2005 Edition), Edward N. Zalta (ed.);online article.
- Mermin, N.D.: "What is Quantum Mechanics Trying to Tell us?"; American Journal of Physics, 66 (1998): 753-767, arXiv:quant-ph/9801057.
- Rovelli, C. & Smerlak, M.: "Relational EPR"; Preprint: arXiv:quant-ph/0604064.
- Rovelli, C.: "Relational Quantum Mechanics"; International Journal of Theoretical Physics 35; 1996: 1637-1678; arXiv:quant-ph/9609002.
- Smolin, L.: "The Bekenstein Bound, Topological Quantum Field Theory and Pluralistic Quantum Field Theory"; Preprint: arXiv:gr-qc/9508064.
- Wheeler, J. A.: "Information, physics, quantum: The search for links"; in Zurek,W., ed.: "Complexity, Entropy and the Physics of Information"; pp 3–28; Addison-Wesley; 1990.
Endnotes
- Wheeler, 1990: pg. 3
- Rovelli, 1996: pg. 2
- Smolin, 1995
- Crane, 1993
- Rovelli & Smerlak, 2006
- Rovelli, 1996: pg. 16
- Find Cifone, Silberstein, Stuckey RBW reference
- Smolin (1995), pg. 13
- Rovelli, 1996: pg. 14
- Rovelli, 1996: pg. 13
.
Category:Quantum Mechanics Category:Quantum Measurement Category:Philosophy of Science Category:Philosophy of Physics

 (represented by a
(represented by a  describing this
describing this  , who is interested in the state of the entire Feynman diagram-physicist-experiment system, and that he likewise has complete information.
, who is interested in the state of the entire Feynman diagram-physicist-experiment system, and that he likewise has complete information.
 and
and  ,
,  . Now, the observer
. Now, the observer  , this observer may characterize the system as follows:
, this observer may characterize the system as follows:

 and
and  are probabilities of finding the system in the respective states, and obviously add up to 1. For our purposes here, we can assume that in a single experiment, the outcome is the
are probabilities of finding the system in the respective states, and obviously add up to 1. For our purposes here, we can assume that in a single experiment, the outcome is the 
 , where
, where  is the Hilbert space inhabited by
is the Hilbert space inhabited by  , after the measurement, some
, after the measurement, some  or
or  where the direction of the arrows in the subscripts corresponds to the outcome of the measurement that
where the direction of the arrows in the subscripts corresponds to the outcome of the measurement that  system, but does not interact with it, the following gives the description of the measurement event according to
system, but does not interact with it, the following gives the description of the measurement event according to 
 . In particular,
. In particular,  , which is specified as:
, which is specified as:




 ,
,  itself interacts with the
itself interacts with the  denote the set of all possible questions that may be "asked" of a quantum system, which we shall denote by
denote the set of all possible questions that may be "asked" of a quantum system, which we shall denote by  ,
,  . We may experimentally find certain relations between these questions:
. We may experimentally find certain relations between these questions:  , corresponding to {intersection, orthogonal sum, orthogonal complement, inclusion, and orthogonality} respectively, where
, corresponding to {intersection, orthogonal sum, orthogonal complement, inclusion, and orthogonality} respectively, where  .
.
 of
of 
 possible
possible  are defined for all
are defined for all  of a system
of a system  the probability that a "yes" answer to a question
the probability that a "yes" answer to a question  will follow the complete question
will follow the complete question  . If
. If  , or it might be fully determined by
, or it might be fully determined by  . There is also a range of intermediate possibilities, and this case is examined below.
. There is also a range of intermediate possibilities, and this case is examined below.
 , the probability
, the probability  of a "yes" answer has certain constraints upon it:
of a "yes" answer has certain constraints upon it:



 ,
, is a
is a  and
and  are two complete questions, then the unitary matrix
are two complete questions, then the unitary matrix  associated with their probability described above satisfies the equality
associated with their probability described above satisfies the equality  , for all
, for all  and
and  .
. as a
as a  as a
as a 
 is
is

 , and are regarded as distinct if they are specified by the same operator but are performed at different times. Because time evolution is a
, and are regarded as distinct if they are specified by the same operator but are performed at different times. Because time evolution is a  has the structure of the set of
has the structure of the set of  that satisfies:
that satisfies:
 , and
, and
 is the
is the