This is an old revision of this page, as edited by Geometry guy (talk | contribs) at 19:50, 24 March 2007 (Minor typos). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 19:50, 24 March 2007 by Geometry guy (talk | contribs) (Minor typos)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)- For other senses of this word, see derivative (disambiguation).
- This article assumes an understanding of algebra, analytic geometry, and the limit. For a non-technical overview of the subject, see Calculus.
| Part of a series of articles about | ||||||
| Calculus | ||||||
|---|---|---|---|---|---|---|
Differential
|
||||||
Integral
|
||||||
Series
|
||||||
Vector
|
||||||
Multivariable
|
||||||
|
Advanced |
||||||
| Specialized | ||||||
| Miscellanea | ||||||
In mathematics, a derivative is the rate of change of a quantity. A derivative is an instantaneous rate of change: it is calculated at a specific instant rather than as an average over time. The process of finding a derivative is called differentiation. The reverse process is integration. The two processes are the central concepts of calculus and the relationship between them is the fundamental theorem of calculus.
For a real-valued function of a single real variable, the derivative at a point equals the slope of the line tangent to the graph of the function at that point. Derivatives can be used to characterize many properties of a function, including
- whether and at what rate the function is increasing or decreasing for a fixed value of the input to the function
- whether and where the function has maximum or minimum values
The concept of a derivative can be extended to functions of more than one variable (see multivariable calculus), to functions of complex variables (see complex analysis) and to many other cases.
Differentiation has many applications throughout all numerate disciplines. For example, in physics, the derivative of the position of a moving body is its velocity and the derivative of the velocity is the acceleration.
History of differentiation
Main article: History of calculusThe modern development of calculus is credited to Isaac Newton and Gottfried Leibniz who worked independently in the late 1600s. Newton began his work in 1666 and Leibniz began his in 1676. However, Leibniz published his first paper in 1684, predating Newton's publication in 1693. There was a bitter controversy between the two men over who first invented calculus which shook the mathematical community in the early 18th century. Both Newton and Leibniz based their work on that of earlier mathematicians. Isaac Barrow (1630 - 1677) is often credited with the early development of what is now called the derivative.
Differentiation and differentiability
Differentiation expresses the rate at which a quantity, y, changes with respect to the change in another quantity, x, on which it has a functional relationship or dependency. Using the symbol Δ (Delta) to refer to change in a quantity, this rate is defined as a limit of difference quotients
which means the limit as approaches 0. In Leibniz's notation for derivatives, the derivative of y with respect to x is written
suggesting the ratio of two infinitesimal quantities. The above expression is pronounced in various ways such as "d y by d x" or "d y over d x". The oral form "d y d x" is often used conversationally, although it may lead to confusion.
In modern (especially pure) mathematics, the use of dependent and independent variables in calculus is no longer common; instead differentiation is defined as a mathematical operation on functions. One precise way to define the derivative is as a limit :
A function is differentiable at a point x if the above limit exists (as a finite real number) at that point. A function is differentiable on an interval if it is differentiable at every point within the interval.
As an alternative, the development of nonstandard analysis in the 20th century showed that Leibniz's original idea of the derivative as a ratio of infinitesimals can be made as rigorous as the formulation in terms of limits.
If a function is not continuous at a point, then there is no tangent line and the function is not differentiable at that point. However, even if a function is continuous at a point, it may not be differentiable there. For example, the function y = |x| is continuous at x = 0, but it is not differentiable there, due to the fact that the limit in the above definition does not exist (the limit from the right is 1 while the limit from the left is −1). Graphically, we see this as a "kink" in the graph at x = 0. Even a function with a smooth graph is not differentiable at a point where its tangent is vertical, such as x = 0 for . Thus, differentiability implies continuity, but not vice versa. One famous example of a function that is continuous everywhere but differentiable nowhere is the Weierstrass function.
The derivative of a function f at x is a quantity which varies if x varies. The derivative is therefore itself a function of x; there are several notations for this function, but f ' is common.
The derivative of a derivative, if it exists, is called a second derivative. Similarly, the derivative of a second derivative is a third derivative, and so on. At a given point or on a given interval, a function may have no derivative, a finite number of successive derivatives, or an infinite number of successive derivatives. On the real line, every polynomial function is infinitely differentiable, meaning that the derivative can be taken at any point, successively, any number of times. After a finite number of differentiations, the function f(x) = 0 is reached, and all subsequent derivatives are 0.
Newton's difference quotient
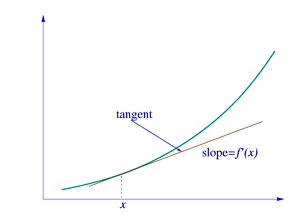


The derivative of a function f at x is geometrically the slope of the tangent line to the graph of f at x. The slope of the tangent line is a limit, the limit of the slopes of the secant lines between two points on a curve, as the distance between the two points goes to zero.
To find the slopes of the nearby secant lines, we represent the horizontal distance between two points by a symbol h, which can be either positive or negative, depending on whether the second point is to the right or the left of the first. The slope of the line through the points (x,f(x)) and (x+h,f(x+h)) is
This expression is Newton's difference quotient. The derivative of f at x is the limit of the value of the difference quotient as the secant lines get closer and closer to the tangent line:
If the derivative of f exists at every point x in the domain, we can define the derivative of f to be the function whose value at a point x is the derivative of f at x.
One cannot obtain the limit by substituting 0 for h, since it will result in division by zero. Instead, one must first modify the numerator to cancel h in the denominator. This process can be long and tedious for complicated functions, and many short cuts are commonly used which simplify the process.
Examples
Consider the graph of f(x) = 2x − 3. Using analytic geometry, the slope of this line can be shown to be 2 at every point. The computations below get the same result using calculus, illustrating the use of the difference quotient.
The derivative and slope are equivalent.
Now consider the function f(x) = x:
For any point x, the slope of the function f(x)=x is .
Notations for differentiation
Lagrange's notation
The simplest notation for differentiation that is in current use is due to Joseph Louis Lagrange and uses the prime mark:
| for the first derivative, | |
| for the second derivative, | |
| for the third derivative, and in general | |
| for the nth derivative. |
Leibniz's notation
The other common notation is Leibniz's notation for differentiation which is named after Gottfried Leibniz. For the function whose value at x is the derivative of f at x, we write:
With Leibniz's notation, we can write the derivative of f at the point a in two different ways:
If the output of f(x) is another variable, for example, if y=f(x), we can write the derivative as:
Higher derivatives are expressed as
- or
for the n-th derivative of f(x) or y respectively. Historically, this came from the fact that, for example, the 3rd derivative is:
which we can loosely write as:
Dropping brackets gives the notation above.
Leibniz's notation allows one to specify the variable for differentiation (in the denominator). This is especially relevant for partial differentiation. It also makes the chain rule easy to remember:
(In the formulation of calculus in terms of limits, the du symbol has been assigned various meanings by various authors. Some authors do not assign a meaning to du by itself, but only as part of the symbol du/dx. Others define "dx" as an independent variable, and define du by du = dx•f '(x). In non-standard analysis du is defined as an infinitesimal. It is also interpreted as the exterior derivative du of a function u. See differential (infinitesimal) for further information.)
Newton's notation
Newton's notation for differentiation (also called the dot notation for differentiation) requires placing a dot over the function name:
and so on.
Newton's notation is mainly used in mechanics, normally for time derivatives such as velocity and acceleration, and in ODE theory. It is usually only used for first and second derivatives, and then, only to denote derivatives with respect to time.
Euler's notation
Euler's notation uses a differential operator, denoted as D, which is prefixed to the function with the variable as a subscript of the operator:
| for the first derivative, | |
| for the second derivative, and | |
| for the nth derivative, provided n ≥ 2. |
This notation can also be abbreviated when taking derivatives of expressions that contain a single variable. The subscript to the operator is dropped and is assumed to be the only variable present in the expression. In the following examples, u represents any expression of a single variable:
| for the first derivative, | |
| for the second derivative, and | |
| for the nth derivative, provided n ≥ 2. |
Euler's notation is useful for stating and solving linear differential equations.
Critical points
Points on the graph of a function where the derivative is equal to zero or the derivative does not exist are called critical points or sometimes stationary points. If the second derivative is positive at a critical point, that point is a local minimum; if negative, it is a local maximum; if zero, it may or may not be a local minimum or local maximum. Taking derivatives and solving for critical points is often a simple way to find local minima or maxima, which can be useful in optimization. In fact, local minima and maxima can only occur at critical points or endpoints. This is related to the extreme value theorem.
Physics
Arguably the most important application of calculus to physics is the concept of the "time derivative"—the rate of change over time—which is required for the precise definition of several important concepts. In particular, the time derivatives of an object's position are significant in Newtonian physics:
- Velocity is the derivative (with respect to time) of an object's displacement (distance from the original position).
- Acceleration is the derivative (with respect to time) of an object's velocity, that is, the second derivative (with respect to time) of an object's position.
- Jerk is the derivative (with respect to time) of an object's acceleration, that is, the third derivative (with respect to time) of an object's position, and second derivative (with respect to time) of an object's velocity.
For example, if an object's position on a curve is given by
then the object's velocity is
and the object's acceleration is
Since the acceleration is constant, the jerk of the object is zero.
Rules for finding the derivative
In many cases, complicated limit calculations by direct application of Newton's difference quotient can be avoided using differentiation rules.
- Constant rule:
- for any real number c
- Constant multiple rule:
- for any real number c (a consequence of the linearity rule below).
- for all functions f and g and all real numbers a and b.
- Power rule: If , for some real number r;
- .
- for all functions f and g.
- unless g is zero.
- Chain rule: If , then
- .
- Inverse function: If the function has an inverse , then
- .
In addition, the derivatives of some common functions are useful to know. See the table of derivatives.
As an example, the derivative of
is
The first term was calculated using the power rule, the second using the chain rule and the last two come from the product rule. The derivatives of sin(x), ln(x) and exp(x) can be found in table of derivatives.
Using derivatives to graph functions
Derivatives are a useful tool for examining the graphs of functions. In particular, the points in the interior of the domain of a real-valued function which take that function to local extrema will all have a first derivative of zero. However, not all critical points are local extrema; for example, f(x)=x has a critical point at x=0, but it has neither a maximum nor a minimum there. The first derivative test and the second derivative test provide ways to determine if the critical points are maxima, minima or neither.
In the case of multidimensional domains, the function will have a partial derivative of zero with respect to each dimension at local extrema. In this case, the Second Derivative Test can still be used to characterize critical points, by considering the eigenvalues of the Hessian matrix of second partial derivatives of the function at the critical point. If all of the eigenvalues are positive, then the point is a local minimum; if all are negative, it is a local maximum. If there are some positive and some negative eigenvalues, then the critical point is a saddle point, and if none of these cases hold then the test is inconclusive (e.g., eigenvalues of 0 and 3).
Once the local extrema have been found, it is usually rather easy to get a rough idea of the general graph of the function, since (in the single-dimensional domain case) it will be uniformly increasing or decreasing except at critical points, and hence (assuming it is continuous) will have values in between its values at the critical points on either side.
Generalizations
Further information: derivative (generalizations)Where a function depends on more than one variable, the concept of a partial derivative is used. Partial derivatives can be thought of informally as taking the derivative of the function with all but one variable held temporarily constant near a point. Partial derivatives are represented as ∂/∂x (where ∂ is a rounded 'd' known as the 'partial derivative symbol'). Some people pronounce the partial derivative symbol as 'del' rather than the 'dee' used for the standard derivative symbol, 'd'.
The concept of derivative can be extended to more general settings. The common thread is that the derivative at a point serves as a linear approximation of the function at that point. Perhaps the most natural situation is that of functions between differentiable manifolds; the derivative at a certain point then becomes a linear transformation between the corresponding tangent spaces and the derivative function becomes a map between the tangent bundles.
In order to differentiate all continuous functions and much more, one defines the concept of distribution and weak derivatives.
For complex functions of a complex variable differentiability is a much stronger condition than that the real and imaginary part of the function are differentiable with respect to the real and imaginary part of the argument. For example, the function f(x + iy) = x + 2iy satisfies the latter, but not the first. See also the article on holomorphic functions.
See also
- Derivative (examples)
- Derivative (generalizations)
- Partial derivative
- Total derivative
- Table of derivatives
- Smooth function
- Differintegral
- Automatic differentiation
- Reciprocal rule
- Chain rule
- History of calculus
References
- Gribbin, John (2002). Science a History. Penguin books. pp. 180–181.
- Howard Eves, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0
- Spivak, ch 10
- Spivak, Michael, Calculus (3rd edition, 1994) Publish or Perish Press. ISBN 0-914098-89-6.
- Thompson, Silvanus Phillips, Calculus made easy : being a very-simplest introduction to those beautiful methods of reckoning which are generally called by the terrifying names of the differential calculus and the integral calculus New York : St. Martin's Press, 1998 ISBN 0-312-18548-0. Introduced by Martin Gardner.
- Larson, Ron; Hostetler, Robert P.; and Edwards, Bruce H. (2003). Calculus of a Single Variable: Early Transcendental Functions (3rd edition). Houghton Mifflin Company. ISBN 0-618-22307-X.
- Anton, Howard (1980). Calculus with analytical geometry.. New York:John Wiley and Sons. ISBN 0-471-03248-4.
Online books
- Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
- Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
- Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
- Crowell, Benjamin, Calculus, Fullerton College, an online textbook
- Garrett, Paul, Notes on First-Year Calculus
- Hussain, Faraz, Understanding Calculus, an online textbook
- Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
- Wikibook of Calculus
External links
- WIMS Function Calculator makes online calculation of derivatives; this software also enables interactive exercises.
- ADIFF online symbolic derivatives calculator.


 approaches 0. In
approaches 0. In 

 . Thus, differentiability implies continuity, but not vice versa. One famous example of a function that is continuous everywhere but differentiable nowhere is the
. Thus, differentiability implies continuity, but not vice versa. One famous example of a function that is continuous everywhere but differentiable nowhere is the 










 .
.







 or
or 














 for any real number c
for any real number c for any
for any  for all functions f and g and all real numbers a and b.
for all functions f and g and all real numbers a and b. , for some
, for some  .
. for all functions f and g.
for all functions f and g. unless g is zero.
unless g is zero. , then
, then .
. has an inverse
has an inverse  , then
, then .
.
