This is an old revision of this page, as edited by DParlevliet (talk | contribs) at 18:19, 5 February 2014 (→With entangled photons and circular polarizers (Walborn e.a.)). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 18:19, 5 February 2014 by DParlevliet (talk | contribs) (→With entangled photons and circular polarizers (Walborn e.a.))(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| Part of a series of articles about |
| Quantum mechanics |
|---|
| Schrödinger equation |
| Background |
| Fundamentals |
| Experiments |
| Formulations |
| Equations |
| Interpretations |
| Advanced topics |
Scientists
|
A delayed choice quantum eraser is a quantum eraser equipment in which the information is erased after detection. A quantum eraser is based on a two-path experiment (like double slit experiment or interferometer) in which the wave of (mostly) a photon is split in two waves, which follow different paths. If both waves combine again at a detector, it will measure an interference pattern. Quantum mechanics states that if it is known which path the photon particle followed, the interference disappears. A Quantum eraser first adds the which-path information, showed the disappearing of the interference, and then erases this information, causing the interference to appear again. In a Delayed choice quantum eraser the which-path information is erased after detection of the photon. This experiment was first proposed by Scully and Drühl and performed by Kim e.a. . The experiment was designed to investigate peculiar consequences of the double slit experiment in quantum mechanics, as well as the consequences of quantum entanglement.
Experiments
Polarizers at the slits
A Quantum eraser which often used in education is based on placing two orthogonal polarizers at the slits of a Double slit experiment, causing the interference to disappear. Then after the slits a polarizer is placed at 45º, which erases the polarised information of the waves, showing the interference again. This experiment is described in double slit experiment. With classical waves the result can also be explained.
Interferometer with 50% mirror

This Quantum eraser is the Mach-Zehnder interferometer, where a light beam (yellow) is split by a 50% mirror in two beams (red and blue). Both beams are reflected by a mirror and cross each other. Finally each beam ends in a separate detector.
In the top diagram only red or blue photons are detected, so no interference is measured. In the bottom diagram with a second beam splitter both outgoing beams has both red and blue photons, without possibility to distinguish, now showing interference in both detectors. The description is also valid for single photons.
In the classical wave description the wave of the photon is split in two by the 50% mirror. In the upper diagram each detector sees only one wave, so there is no interference with the other wave. In the lower diagram both waves are mixed, so each detector sees both waves, which interfere. The wave determines the possibility of absorption.
The phase difference is introduced along the two paths because of the different effects of passing through a glass plate, being reflected off its first surface, or passing through the back surface of a semi-silvered beam splitter and being reflected by the back (inner side) of the reflective surface.
The result is that waves pass out of both the top upwards exit, and also the top-right exit. Specifically, waves passing out the top exit interfere destructively, whereas waves passing out the upper right side exit interfere constructively.
With entangled photons and particle-path detectors (Kim e.a.)
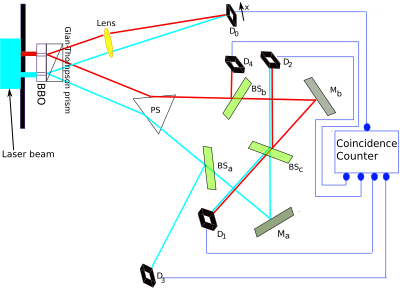
An experimental setup is as follows. A high intensity laser radiates a double slit (vertical black line in the upper left hand corner of the diagram). After the slits a beta barium borate crystal (BBO) causes spontaneous parametric down conversion (SPDC), which generates now and then two identical entangled photons with 1/2 the frequency of the laser photons, in the "red" or "blue" area of the BBO. These photons are caused to diverge and follow two paths by a Glan-Thompson Prism.
One of the photons, the "signal" photon, goes upwards, through a lens, to the target detector D0.
The other photon, the "idler" photon, goes downwards and is deflected by a prism that sends it along divergent paths, depending on whether it came from the "red" or "blue" BBO area.
Beyond each path a 50% mirror acts as a beam splitter (green blocks), resulting in a 50% chance to pass through and a 50% chance reflecting to detectors D3 or D4. The photons which pass through are reflected by 100% mirrors (gray-green blocks) to the detectors D1 or D2. Where both beams cross a third 50% mirror is placed, which reflect 50% of each beam to the other detector.
Because of this arrangement:
- If the photon is recorded at detector D3, it can only be a "blue" photon.
- If the photon is recorded at detector D4, it can only be a "red" photon.
If the photon is recorded at detector D1 or D2, it has a 50% chance to be a "blue" photon and 50% chance to be a "red" one. So when detected by D1 or D2, one cannot know through which slit the photon has traveled. It is said that the red/blue information has been "erased".
Observed results
A coincidence counter selects from the target detector D0 only the events which coincide with the other detectors. This includes a delay of 8 ns to compensate for the 2.5 meter longer path to the other detectors.
- When events were counted which coincided with D3 or D4, there was no interference.
- When events were counted which coincided with D1 or D2, there was an interference pattern.
This is in agreement with the statement in Quantum mechanics that when the path is known, the interference pattern disappears. But most remarkable is that the photons in D0 seem to know that they will not form an interference pattern 8 ns before the path information is detected by D3 or D4. This seems to suggest that the probability of photon detection depends on a future event.
With classical wave physics the absence of interference with D3/D4 can be explained, because when an photon is emitted in the red area of the BBO, there will be no wave in the blue area (and vice versa), so no two waves to interfere. However the appearance of the interference with D1/D2 cannot be explained classical.
Some have interpreted this result to mean that the delayed choice to observe or not observe the path of the idler photon will change the outcome of an event in the past. However, an interference pattern may only be observed after the idlers have been detected (i.e., at D1 or D2).
Note that the total pattern of all signal photons at D0, whose entangled idlers went to multiple different detectors, will never show interference regardless of what happens to the idler photons. One can get an idea of how this works by looking carefully at both the graph of the subset of signal photons whose idlers went to detector D1 (fig. 3 in the paper), and the graph of the subset of signal photons whose idlers went to detector D2 (fig. 4), and observing that the peaks of the first interference pattern line up with the troughs of the second and vice versa (noted in the paper as "a π phase shift between the two interference fringes"), so that the sum of the two will not show interference.
With entangled photons and circular polarizers (Walborn e.a.)

In this Delayed quantum eraser a beta barium borate (BBO) crystal, radiated by a strong laser, will generate now and then two entangled photons. One photon (yellow path) goes through a double slit to signal detector Ds, with circular polarizer Q1 or Q2 in each path. They are rotated 90° to each other, producing a circular polarization in opposite directions. The other photon (green path) goes to detector Dp, with a linear polarizer cube POL in the path. Only photons in Ds are registered which coincide with photons in Dp. Dp is situated closer to the BBO then Ds, so photons are first detected by Dp. The results were:
- Without Q1/Q2 and POL there was an interference pattern in Ds
- With Q1/Q2 there was no interference.
- With Q1/Q2 and POL, adjusted on the Q1 fast axis, there was interference.
- With Q1/Q2 and POL, adjusted on the Q2 fast axis, there was interference, but 180º shifted with 3.
- 1-4 with Dp on a larger distance then Ds gives the same result. This is a delayed eraser, because the photon in Dp is detected later then in Ds
The explanation with quantum mechanics is that Q1/Q2 marks the red path and the blue path beams. So one could detect which path the photon went, also when this measurement is not actually done (as in 2). This removes the interference pattern. When placing POL at a suitable angle, the polarization information is erased, so it is no longer possible to know by which path the photon travelled. Therefore the interference pattern is restored.
In the classical wave description Q1 and Q2 are quarter-wave plates which have orthogonal a "fast" and "slow" axis. The slow axis has 90° phase delay to the fast axis. The axis of Q1 and Q2 are orthogonal (see figure). In 3 and 4 the POL forces the idler wave in a certain direction. Because of entanglement the signal wave will be forced at 90° of the idler wave. In 3 the POL forces the signal wave polarization to be parallel to the fast axis of Q2. Then the output polarisation does not rotate, but is linear, with Q1 having -90° phase shift (slow axis) with Q2. In 4 Q1 is +90° phase shift with Q2. Therefore 3 and 4 gives interference patterns which are 180° shifted, as has been measured. In 2 the incoming polarization can be resolve in two polarizations on the F and S axis, which each give the same result as 3 en 4. So 2 is not an absence of interference, but the sum of two interference patterns which are shifted 180°. With waves the crucial moments are not the detection, but the polarisers. In there is no delayed choice, but the property of entangled photons that if POL changes the polarization of the idler photon. The signal photon will follow directly, also in front of Q1/Q2, although these are situated closer to the BBO then POL.
Discussion
Details pertaining to retrocausality in the Kim experiment
In their paper, Kim, et al. explain that the concept of complementarity is one of the most basic principles of quantum mechanics. According to the Heisenberg Uncertainty Principle, it is not possible to precisely measure both the position and the momentum of a quantum particle at the same time. In other words, position and momentum are complementary. In 1927, Niels Bohr maintained that quantum particles have both "wave-like" behavior and "particle-like" behavior, but can exhibit only one kind of behavior under conditions that prevent exhibiting the complementary characteristics. This complementarity has come to be known as the wave-particle duality of quantum mechanics. Richard Feynman believed that the presence of these two aspects under conditions that prevent their simultaneous manifestation is the basic mystery of quantum mechanics.
According to Kim, et al., "The actual mechanisms that enforce complementarity vary from one experimental situation to another." In the double-slit experiment, the common wisdom is that complementarity makes it seemingly impossible to determine which slit the photon passes through without at the same time disturbing it enough to destroy the interference pattern. A 1982 paper by Scully and Drühl circumvented the issue of disturbance due to direct measurement of the photon, according to Kim, et al. Scully and Drühl "found a way around the position-momentum uncertainty obstacle and proposed a quantum eraser to obtain which-path or particle-like information without introducing large uncontrolled phase factors to disturb the interference."
Scully and Drühl found that there is no interference pattern when which-path information is obtained, even if this information was obtained without directly observing the original photon, but that if you somehow "erase" the which-path information, an interference pattern is again observed.
In the delayed choice quantum eraser discussed here, the pattern exists even if the which-path information is erased shortly later in time than the signal photons hit the primary detector. However, the interference pattern can only be seen retroactively once the idler photons have already been detected and the experimenter has obtained information about them, with the interference pattern being seen when the experimenter looks at particular subsets of signal photons that were matched with idlers that went to particular detectors.
The main stumbling block for using retrocausality to communicate information
The total pattern of signal photons at the primary detector never shows interference, so it is not possible to deduce what will happen to the idler photons by observing the signal photons alone, which would open up the possibility of gaining information faster-than-light (since one might deduce this information before there had been time for a message moving at the speed of light to travel from the idler detector to the signal photon detector) or even gaining information about the future (since as noted above, the signal photons may be detected at an earlier time than the idlers), both of which would qualify as violations of causality in physics. The apparatus under discussion here could not communicate information in a retro-causal manner because it takes another signal, one which must arrive via a process that can go no faster than the speed of light, to sort the superimposed data in the signal photons into four streams that reflect the states of the idler photons at their four distinct detection screens.
In fact, a theorem proved by Phillippe Eberhard shows that if the accepted equations of relativistic quantum field theory are correct, it should never be possible to experimentally violate causality using quantum effects (see reference for a treatment emphasizing the role of conditional probabilities).
Yet there are those who persevere in attempting to communicate retroactively
Some physicists have speculated about the possibility that these experiments might be changed in a way that would be consistent with previous experiments, yet which could allow for experimental causality violations.
See also
- Afshar experiment
- Wheeler's delayed choice experiment
- The transactional interpretation of quantum mechanics
- Retrocausality
- Quantum radar
- Wheeler-Feynman absorber theory
References
- name="Scully">M.O. Scully and K. Drühl (1982). Physical Review A. 25: 2208.
{{cite journal}}: Missing or empty|title=(help) - ^ Kim, Yoon-Ho (2000). "A Delayed Choice Quantum Eraser". Physical Review Letters. 84: 1–5. arXiv:quant-ph/9903047. Bibcode:2000PhRvL..84....1K. doi:10.1103/PhysRevLett.84.1.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Jacques, Vincent; Wu, E; Grosshans, Frédéric; Treussart, François; Grangier, Philippe; Aspect, Alain; Rochl, Jean-François (2007). "Experimental Realization of Wheeler's Delayed-Choice Gedanken Experiment". Science. 315 (5814): pp. 966–968. arXiv:quant-ph/0610241. Bibcode:2007Sci...315..966J. doi:10.1126/science.1136303. PMID 17303748.
{{cite journal}}:|pages=has extra text (help) - Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. p. 198. ISBN 0-375-41288-3.
- ^ Walborn, S. P. (2002). "Double-Slit Quantum Eraser". Phys. Rev. A. 65 (3): 033818. doi:10.1103/PhysRevA.65.033818.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - see Waveplate#Quarter-wave plate
- Scully, Marlan O. (1982). "Quantum eraser: A proposed photon correlation experiment concerning observation and "delayed choice" in quantum mechanics". Physical Review A. 25 (4): 2208–2213. Bibcode:1982PhRvA..25.2208S. doi:10.1103/PhysRevA.25.2208.
{{cite journal}}: Unknown parameter|coauthors=ignored (|author=suggested) (help) - Eberhard, Phillippe H. (1989). "Quantum field theory cannot provide faster-than-light communication". Foundations of Physics Letters. 2 (2): p. 127–149. Bibcode:1989FoPhL...2..127E. doi:10.1007/BF00696109.
{{cite journal}}:|pages=has extra text (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - Bram Gaasbeek. Demystifying the Delayed Choice Experiments. arXiv preprint, 22 July 2010.
- John G. Cramer. NASA Goes FTL - Part 2: Cracks in Nature's FTL Armor. "Alternate View" column, Analog Science Fiction and Fact, February 1995.
- Paul J. Werbos, Ludmila Dolmatova. The Backwards-Time Interpretation of Quantum Mechanics - Revisited With Experiment. arXiv preprint, 7 August 2000.
External links
- presentation of the experiment
- basic delayed choice experiment
- delayed choice quantum eraser
- the notebook of philosophy and physics
- Comprehensive experimental test of quantum erasure, Alexei Trifonov, Gunnar Bjork, Jonas Soderholm, and Tedros Tsegaye (doi:10.1140/epjd/e20020030)
- A non-local quantum eraser (June 2012; 12 authors, including Anton Zeilinger)
