| It has been suggested that this article be merged into 3D Morphable Model. (Discuss) Proposed since August 2024. |
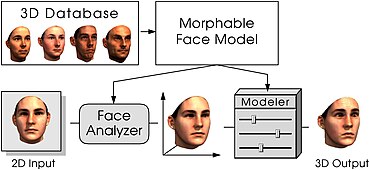
In computer vision and computer graphics, the 3D Face Morphable Model (3DFMM) is a generative technique for modeling textured 3D faces. The generation of new faces is based on a pre-existing database of example faces acquired through a 3D scanning procedure. All these faces are in dense point-to-point correspondence, which enables the generation of a new realistic face (morph) by combining the acquired faces. A new 3D face can be inferred from one or multiple existing images of a face or by arbitrarily combining the example faces. 3DFMM provides a way to represent face shape and texture disentangled from external factors, such as camera parameters and illumination.
The 3D Morphable Model (3DMM) is a general framework that has been applied to various objects other than faces, e.g., the whole human body, specific body parts, and animals. 3DMMs were first developed to solve vision tasks by representing objects in terms of the prior knowledge that can be gathered from that object class. The prior knowledge is statistically extracted from a database of 3D examples and used as a basis to represent or generate new plausible objects of that class. Its effectiveness lies in the ability to efficiently encode this prior information, enabling the solution of otherwise ill-posed problems (such as single-view 3D object reconstruction).
Historically, face models have been the first example of morphable models, and the field of 3DFMM remains a very active field of research as today. In fact, 3DFMM has been successfully employed in face recognition, entertainment industry (gaming and extended reality, virtual try on, face replacement, face reenactment), digital forensics, and medical applications.
Modeling
In general, 3D faces can be modeled by three variational components extracted from the face dataset:
- shape model - model of the distribution of geometrical shape across different subjects
- expression model - model of the distribution of geometrical shape across different facial expressions
- appearance model - model of the distribution of surface textures (color and illumination)
Shape modeling

The 3DFMM uses statistical analysis to define a statistical shape space, a vectorial space equipped with a probability distribution, or prior. To extract the prior from the example dataset, all the 3D faces must be in a dense point-to-point correspondence. This means that each point has the same semantical meaning on each face (e.g., nose tip, edge of the eye). In this way, by fixing a point, we can, for example, derive the probability distribution of the texture's red channel values over all the faces. A face shape of vertices is defined as the vector containing the 3D coordinates of the vertices in a specified order, that is . A shape space is regarded as a -dimensional space that generates plausible 3D faces by performing a lower-dimensional () parametrization of the database. Thus, a shape can be represented through a generator function by the parameters , . The most common statistical technique used in 3DFMM to generate the shape space is Principal Component Analysis (PCA), that generates a basis that maximizes the variance of the data. Performing PCA, the generator function is linear and defined as where is the mean over the training data and is the matrix that contains the most dominant eigenvectors.
Using a unique generator function for the whole face leads to the imperfect representation of finer details. A solution is to use local models of the face by segmenting important parts such as the eyes, mouth, and nose.
Expression modeling
The modeling of the expression is performed by explicitly subdividing the representation of the identity from the facial expression. Depending on how identity and expression are combined, these methods can be classified as additive, multiplicative, and nonlinear.
The additive model is defined as a linear model and the expression is an additive offset with respect to the identity where , and , are the matrices basis and the coefficients vectors of the shape and expression space, respectively. With this model, given the 3D shape of a subject in a neutral expression and in a particular expression , we can transfer the expression to a different subject by adding the offset . Two PCAs can be performed to learn two different spaces for shape and expression.
In a multiplicative model, shape and expression can be combined in different ways. For example, by exploiting operators that transform a neutral expression into a target blendshape we can writewhere and are vectors to correct to the target expression.
The nonlinear model uses nonlinear transformations to represent an expression.
Appearance modeling
The color information id often associated to each vertex of a 3D shape. This one-to-one correspondence allows us to represent appearance analogously to the linear shape model where is the coefficients vector defined over the basis matrix . PCA can be again be used to learn the appearance space.
History
Facial recognition can be considered the field that originated the concepts that later on converged into the formalization of the morphable models. The eigenface approach used in face recognition represented faces in a vector space and used principal component analysis to identify the main modes of variation. However, this method had limitations: it was constrained to fixed poses and illumination and lacked an effective representation of shape differences. As a result, changes in the eigenvectors did not accurately represent shifts in facial structures but caused structures to fade in and out. To address these limitations, researchers added an eigendecomposition of 2D shape variations between faces. The original eigenface approach aligned images based on a single point, while new methods established correspondences on many points. Landmark-based face warping was introduced by Craw and Cameron (1991), and the first statistical shape model, Active Shape Model, was proposed by Cootes et al. (1995). This model used shape alone, but Active Appearance Model by Cootes et al. (1998) combined shape and appearance. Since these 2D methods were effective only for fixed poses and illumination, they were extended by Vetter and Poggio (1997) to handle more diverse settings. Even though separating shape and texture was effective for face representation, handling pose and illumination variations required many separate models. On the other hand, advances in 3D computer graphics showed that simulating pose and illumination variations was straightforward. The combination of graphics methods with face modeling led to the first formulation of 3DMMs by Blanz and Vetter (1999). The analysis-by-synthesis approach enabled the mapping of the 3D and 2D domains and a new representation of 3D shape and appearance. Their work is the first to introduce a statistical model for faces that enabled 3D reconstruction from 2D images and a parametric face space for controlled manipulation.
In the original definition of Blanz and Vetter, the shape of a face is represented as the vector that contains the 3D coordinates of the vertices. Similarly, the texture is represented as a vector that contains the three RGB color channels associated with each corresponding vertex. Due to the full correspondence between exemplar 3D faces, new shapes and textures can be defined as a linear combination of the example faces:Thus, a new face shape and texture is parametrized by the shape and texture coefficients . To extract the statistics from the dataset, they performed PCA to generate the shape space of dimension to and used a linear model for shape and appearance modeling. In this case, a new model can be generated in the orthogonal basis using the shape and the texture eigenvector and , respectively:
where and are the mean shape and texture of the dataset.
Publicly available databases
In the following table, we list the publicly available databases of human faces that can be used for the 3DFMM.
| Year | Geometry | Appearance | Size | Download | Institution | |
|---|---|---|---|---|---|---|
| Basel Face Model 2009 | 2009 | shape | per-vertex | 100 individuals in neutral expression | Link | University of Basel |
| FaceWarehouse | 2014 | shape, expression | - | 150 individuals in 20 different expressions | Link | Zhejiang University |
| Large Scale Facial Model (LSFM) | 2016 | shape | - | 9,663 individuals | Link | Imperial College London |
| Surrey Face Model | 2016 | shape, expression (multi-resolution) | per-vertex | 169 individuals | Link | University of Surrey |
| Basel Face Model 2017 | 2017 | shape, expression | per-vertex | 200 individuals and 160 expression scans | Link | University of Basel |
| Liverpool-York Head Model (LYHM) | 2017 | shape (full head - no hair, no eyes) | per-vertex | 1,212 individuals | Link | University of York, Alder Hey Hospital |
| Faces Learned with an Articulated Model and Expressions (FLAME) | 2017 | shape (full head - no hair), expression, head pose | texture | 3,800 individuals for shape, 8,000 for head pose, 21,000 for expression | Link | University of Southern California, Max Planck Institute for Intelligent Systems |
| Convolutional Mesh Autoencoder (CoMA) | 2018 | shape (full head - no hair), expression | - | 2 individuals in 12 extreme expressions | Link | Max Planck Institute for Intelligent Systems |
| Morphable Face Albedo Model | 2020 | - | per-vertex diffuse and specular albedo | 73 individuals | Link | University of York |
| FaceVerse | 2022 | shape | texture | 128 individuals in 21 different expressions | Link | Tsinghua University |
See also
References
- ^ Blanz, Volker; Vetter, Thomas (1999-07-01). "A morphable model for the synthesis of 3D faces". Proceedings of the 26th annual conference on Computer graphics and interactive techniques - SIGGRAPH '99. USA: ACM Press/Addison-Wesley Publishing Co. pp. 187–194. doi:10.1145/311535.311556. hdl:11858/00-001M-0000-0013-E751-6. ISBN 978-0-201-48560-8.
- ^ Egger, Bernhard; Smith, William A. P.; Tewari, Ayush; Wuhrer, Stefanie; Zollhoefer, Michael; Beeler, Thabo; Bernard, Florian; Bolkart, Timo; Kortylewski, Adam; Romdhani, Sami; Theobalt, Christian; Blanz, Volker; Vetter, Thomas (31 October 2020). "3D Morphable Face Models—Past, Present, and Future". ACM Transactions on Graphics. 39 (5): 1–38. doi:10.1145/3395208. hdl:21.11116/0000-0007-1CF5-6.
- Allen, Brett; Curless, Brian; Popović, Zoran (2003-07-01). "The space of human body shapes: reconstruction and parameterization from range scans". ACM Trans. Graph. 22 (3): 587–594. doi:10.1145/882262.882311. ISSN 0730-0301.
- Loper, Matthew; Mahmood, Naureen; Romero, Javier; Pons-Moll, Gerard; Black, Michael J. (2015-10-26). "SMPL: a skinned multi-person linear model". ACM Trans. Graph. 34 (6): 248:1–248:16. doi:10.1145/2816795.2818013. ISSN 0730-0301.
- Khamis, Sameh; Taylor, Jonathan; Shotton, Jamie; Keskin, Cem; Izadi, Shahram; Fitzgibbon, Andrew (June 2015). "Learning an efficient model of hand shape variation from depth images". 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. pp. 2540–2548. doi:10.1109/CVPR.2015.7298869. ISBN 978-1-4673-6964-0.
- Dai, Hang; Pears, Nick; Smith, William (May 2018). "A Data-Augmented 3D Morphable Model of the Ear". 2018 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2018). IEEE. pp. 404–408. doi:10.1109/FG.2018.00065. ISBN 978-1-5386-2335-0.
- Sun, Yifan; Murata, Noboru (March 2020). "CAFM: A 3D Morphable Model for Animals". 2020 IEEE Winter Applications of Computer Vision Workshops (WACVW). IEEE. pp. 20–24. doi:10.1109/WACVW50321.2020.9096941. ISBN 978-1-7281-7162-3.
- Blanz, V.; Romdhani, S.; Vetter, T. (2002). "Face identification across different poses and illuminations with a 3D morphable model". Proceedings of Fifth IEEE International Conference on Automatic Face Gesture Recognition. IEEE. pp. 202–207. doi:10.1109/AFGR.2002.1004155. ISBN 978-0-7695-1602-8.
- Lombardi, Stephen; Saragih, Jason; Simon, Tomas; Sheikh, Yaser (2018-07-30). "Deep appearance models for face rendering". ACM Trans. Graph. 37 (4): 68:1–68:13. arXiv:1808.00362. doi:10.1145/3197517.3201401. ISSN 0730-0301.
- Weise, Thibaut; Li, Hao; Van Gool, Luc; Pauly, Mark (2009-08-01). "Face/Off: Live facial puppetry". Proceedings of the 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation (PDF). SCA '09. New York, NY, USA: Association for Computing Machinery. pp. 7–16. doi:10.1145/1599470.1599472. ISBN 978-1-60558-610-6.
- Bronstein, Alexander M.; Bronstein, Michael M.; Kimmel, Ron (September 2007). "Calculus of Nonrigid Surfaces for Geometry and Texture Manipulation". IEEE Transactions on Visualization and Computer Graphics. 13 (5): 902–913. doi:10.1109/TVCG.2007.1041. ISSN 1077-2626.
- Blanz, Volker; Scherbaum, Kristina; Vetter, Thomas; Seidel, Hans-Peter (September 2004). "Exchanging Faces in Images". Computer Graphics Forum. 23 (3): 669–676. doi:10.1111/j.1467-8659.2004.00799.x. ISSN 0167-7055.
- Thies, Justus; Zollhöfer, Michael; Nießner, Matthias; Valgaerts, Levi; Stamminger, Marc; Theobalt, Christian (2015-11-02). "Real-time expression transfer for facial reenactment". ACM Trans. Graph. 34 (6): 183:1–183:14. doi:10.1145/2816795.2818056. ISSN 0730-0301.
- Cozzolino, Davide; Rossler, Andreas; Thies, Justus; Niesner, Matthias; Verdoliva, Luisa (October 2021). "ID-Reveal: Identity-aware DeepFake Video Detection". 2021 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE. pp. 15088–15097. arXiv:2012.02512. doi:10.1109/ICCV48922.2021.01483. ISBN 978-1-6654-2812-5.
- Mueller, A.A.; Paysan, P.; Schumacher, R.; Zeilhofer, H.-F.; Berg-Boerner, B.-I.; Maurer, J.; Vetter, T.; Schkommodau, E.; Juergens, P.; Schwenzer-Zimmerer, K. (December 2011). "Missing facial parts computed by a morphable model and transferred directly to a polyamide laser-sintered prosthesis: an innovation study". British Journal of Oral and Maxillofacial Surgery. 49 (8): e67 – e71. doi:10.1016/j.bjoms.2011.02.007. ISSN 0266-4356. PMID 21458119.
- ^ Huber, Patrik; Hu, Guosheng; Tena, Rafael; Mortazavian, Pouria; Koppen, Willem P.; Christmas, William J.; Rätsch, Matthias; Kittler, Josef (February 2016). "A Multiresolution 3D Morphable Face Model and Fitting Framework". Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications. pp. 79–86. doi:10.5220/0005669500790086. ISBN 978-989-758-175-5.
- ^ Brunton, Alan; Salazar, Augusto; Bolkart, Timo; Wuhrer, Stefanie (November 2014). "Review of statistical shape spaces for 3D data with comparative analysis for human faces". Computer Vision and Image Understanding. 128: 2. arXiv:1209.6491. doi:10.1016/j.cviu.2014.05.005. ISSN 1077-3142.
- De Smet, Michaël; Van Gool, Luc (2011). "Optimal Regions for Linear Model-Based 3D Face Reconstruction". In Kimmel, Ron; Klette, Reinhard; Sugimoto, Akihiro (eds.). Computer Vision – ACCV 2010. Lecture Notes in Computer Science. Vol. 6494. Berlin, Heidelberg: Springer. pp. 276–289. doi:10.1007/978-3-642-19318-7_22. ISBN 978-3-642-19318-7.
- Blanz, V.; Basso, C.; Poggio, T.; Vetter, T. (September 2003). "Reanimating Faces in Images and Video". Computer Graphics Forum. 22 (3): 641–650. doi:10.1111/1467-8659.t01-1-00712. ISSN 0167-7055.
- Bouaziz, Sofien; Wang, Yangang; Pauly, Mark (2013-07-21). "Online modeling for realtime facial animation". ACM Trans. Graph. 32 (4): 40:1–40:10. doi:10.1145/2461912.2461976. ISSN 0730-0301.
- ^ Li, Tianye; Bolkart, Timo; Black, Michael J.; Li, Hao; Romero, Javier (2017-11-20). "Learning a model of facial shape and expression from 4D scans". ACM Trans. Graph. 36 (6): 194:1–194:17. doi:10.1145/3130800.3130813. ISSN 0730-0301.
- Ichim, Alexandru-Eugen; Kadleček, Petr; Kavan, Ladislav; Pauly, Mark (2017-07-20). "Phace: physics-based face modeling and animation". ACM Trans. Graph. 36 (4): 153:1–153:14. doi:10.1145/3072959.3073664. ISSN 0730-0301.
- Koppen, Paul; Feng, Zhen-Hua; Kittler, Josef; Awais, Muhammad; Christmas, William; Wu, Xiao-Jun; Yin, He-Feng (2018-02-01). "Gaussian mixture 3D morphable face model". Pattern Recognition. 74: 617–628. Bibcode:2018PatRe..74..617K. doi:10.1016/j.patcog.2017.09.006. ISSN 0031-3203.
- Craw, Ian; Cameron, Peter (1991). "Parameterising Images for Recognition and Reconstruction". In Mowforth, Peter (ed.). BMVC91. London: Springer. pp. 367–370. doi:10.1007/978-1-4471-1921-0_52. ISBN 978-1-4471-1921-0.
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. (January 1995). "Active Shape Models-Their Training and Application". Computer Vision and Image Understanding. 61 (1): 38–59. doi:10.1006/cviu.1995.1004. ISSN 1077-3142.
- Cootes, T.F.; Edwards, G.J.; Taylor, C.J. (June 2001). "Active appearance models". IEEE Transactions on Pattern Analysis and Machine Intelligence. 23 (6): 681–685. doi:10.1109/34.927467.
- Vetter, T.; Poggio, T. (July 1997). "Linear object classes and image synthesis from a single example image". IEEE Transactions on Pattern Analysis and Machine Intelligence. 19 (7): 733–742. doi:10.1109/34.598230. hdl:11858/00-001M-0000-0013-ECA6-4.
- Paysan, Pascal; Lüthi, Marcel; Albrecht, Thomas; Lerch, Anita; Amberg, Brian; Santini, Francesco; Vetter, Thomas (2009). "Face Reconstruction from Skull Shapes and Physical Attributes". In Denzler, Joachim; Notni, Gunther; Süße, Herbert (eds.). Pattern Recognition. Lecture Notes in Computer Science. Vol. 5748. Berlin, Heidelberg: Springer. pp. 232–241. doi:10.1007/978-3-642-03798-6_24. ISBN 978-3-642-03798-6.
- Chen Cao; Yanlin Weng; Shun Zhou; Yiying Tong; Kun Zhou (March 2014). "FaceWarehouse: A 3D Facial Expression Database for Visual Computing". IEEE Transactions on Visualization and Computer Graphics. 20 (3): 413–425. doi:10.1109/TVCG.2013.249. ISSN 1077-2626. PMID 24434222.
- Booth, James; Roussos, Anastasios; Zafeiriou, Stefanos; Ponniah, Allan; Dunaway, David (June 2016). "A 3D Morphable Model Learnt from 10,000 Faces". 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. pp. 5543–5552. doi:10.1109/CVPR.2016.598. hdl:10871/31965. ISBN 978-1-4673-8851-1.
- Gerig, Thomas; Morel-Forster, Andreas; Blumer, Clemens; Egger, Bernhard; Luthi, Marcel; Schoenborn, Sandro; Vetter, Thomas (May 2018). "Morphable Face Models - An Open Framework". 2018 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2018). IEEE. pp. 75–82. arXiv:1709.08398. doi:10.1109/FG.2018.00021. ISBN 978-1-5386-2335-0.
- Dai, Hang; Pears, Nick; Smith, William; Duncan, Christian (October 2017). "A 3D Morphable Model of Craniofacial Shape and Texture Variation". 2017 IEEE International Conference on Computer Vision (ICCV). IEEE. pp. 3104–3112. doi:10.1109/ICCV.2017.335. ISBN 978-1-5386-1032-9.
- Ranjan, Anurag; Bolkart, Timo; Sanyal, Soubhik; Black, Michael J. (2018). "Generating 3D Faces Using Convolutional Mesh Autoencoders". In Ferrari, Vittorio; Hebert, Martial; Sminchisescu, Cristian; Weiss, Yair (eds.). Computer Vision – ECCV 2018. Lecture Notes in Computer Science. Vol. 11207. Cham: Springer International Publishing. pp. 725–741. doi:10.1007/978-3-030-01219-9_43. ISBN 978-3-030-01219-9.
- Smith, William A. P.; Seck, Alassane; Dee, Hannah; Tiddeman, Bernard; Tenenbaum, Joshua B.; Egger, Bernhard (June 2020). "A Morphable Face Albedo Model". 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. pp. 5010–5019. arXiv:2004.02711. doi:10.1109/CVPR42600.2020.00506. ISBN 978-1-7281-7168-5.
- Wang, Lizhen; Chen, Zhiyuan; Yu, Tao; Ma, Chenguang; Li, Liang; Liu, Yebin (June 2022). "FaceVerse: a Fine-grained and Detail-controllable 3D Face Morphable Model from a Hybrid Dataset". 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. pp. 20301–20310. arXiv:2203.14057. doi:10.1109/CVPR52688.2022.01969. ISBN 978-1-6654-6946-3.
External links
- "3D Morphable Models". Retrieved 2024-07-08.
- "Curated List of 3D Morphable Model Software and Data". GitHub. Retrieved 2024-07-11.
- "Tutorial on 3D Morphable Models @ Symposium on Geometry Processing 2022". YouTube. 28 June 2022. Retrieved 2024-07-12.
- "What is a Linear 3D Morphable Face Model?". YouTube. 5 April 2020. Retrieved 2024-07-12.
 of
of  vertices is defined as the vector containing the 3D coordinates of the
vertices is defined as the vector containing the 3D coordinates of the  vertices in a specified order, that is
vertices in a specified order, that is  . A shape space is regarded as a
. A shape space is regarded as a  -dimensional space that generates plausible 3D faces by performing a lower-dimensional (
-dimensional space that generates plausible 3D faces by performing a lower-dimensional ( ) parametrization of the database. Thus, a shape
) parametrization of the database. Thus, a shape  by the parameters
by the parameters  ,
,  . The most common statistical technique used in 3DFMM to generate the shape space is
. The most common statistical technique used in 3DFMM to generate the shape space is  where
where  is the mean over the training data and
is the mean over the training data and  is the matrix that contains the
is the matrix that contains the  where
where  ,
, and
and  ,
, are the matrices basis and the coefficients vectors of the shape and expression space, respectively. With this model, given the 3D shape of a subject in a neutral expression
are the matrices basis and the coefficients vectors of the shape and expression space, respectively. With this model, given the 3D shape of a subject in a neutral expression  and in a particular expression
and in a particular expression  , we can transfer the expression to a different subject by adding the offset
, we can transfer the expression to a different subject by adding the offset  . Two PCAs can be performed to learn two different spaces for shape and expression.
. Two PCAs can be performed to learn two different spaces for shape and expression.
 operators
operators  that transform a neutral expression into a target blendshape we can write
that transform a neutral expression into a target blendshape we can write where
where  and
and  are vectors to correct to the target expression.
are vectors to correct to the target expression.
 where
where  is the coefficients vector defined over the basis matrix
is the coefficients vector defined over the basis matrix  . PCA can be again be used to learn the appearance space.
. PCA can be again be used to learn the appearance space.
 that contains the 3D coordinates of the
that contains the 3D coordinates of the  that contains the three
that contains the three  and textures
and textures  can be defined as a linear combination of the
can be defined as a linear combination of the  example faces:
example faces: Thus, a new face shape and texture is parametrized by the shape
Thus, a new face shape and texture is parametrized by the shape  and texture coefficients
and texture coefficients  . To extract the statistics from the dataset, they performed PCA to generate the shape space of dimension to
. To extract the statistics from the dataset, they performed PCA to generate the shape space of dimension to  and
and  , respectively:
, respectively:

 and
and  are the mean shape and texture of the dataset.
are the mean shape and texture of the dataset.