| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Acousto-optic modulator" – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) |
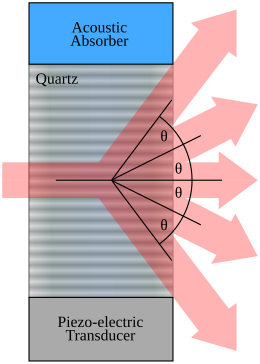
An acousto-optic modulator (AOM), also called a Bragg cell or an acousto-optic deflector (AOD), uses the acousto-optic effect to diffract and shift the frequency of light using sound waves (usually at radio-frequency). They are used in lasers for Q-switching, telecommunications for signal modulation, and in spectroscopy for frequency control. A piezoelectric transducer is attached to a material such as glass. An oscillating electric signal drives the transducer to vibrate, which creates sound waves in the material. These can be thought of as moving periodic planes of expansion and compression that change the index of refraction. Incoming light scatters (see Brillouin scattering) off the resulting periodic index modulation and interference occurs similar to Bragg diffraction. The interaction can be thought of as a three-wave mixing process resulting in sum-frequency generation or difference-frequency generation between phonons and photons.
Principles of operation
A typical AOM operates under Bragg condition, where the incident light comes at Bragg angle from the perpendicular of the sound wave's propagation.

Diffraction
When the incident light beam is at Bragg angle, a diffraction pattern emerges where an order of diffracted beam occurs at each angle θ that satisfies:
Here, m = ..., −2, −1, 0, +1, +2, ... is the order of diffraction, λ is the wavelength of light in vacuum, and Λ is the wavelength of the sound. Note that m = 0 order travels in the same direction as the incident beam.
Diffraction from a sinusoidal modulation in a thin crystal mostly results in the m = −1, 0, +1 diffraction orders. Cascaded diffraction in medium thickness crystals leads to higher orders of diffraction. In thick crystals with weak modulation, only phasematched orders are diffracted; this is called Bragg diffraction. The angular deflection can range from 1 to 5000 beam widths (the number of resolvable spots). Consequently, the deflection is typically limited to tens of milliradians.
The angular separation between adjacent orders for Bragg diffraction is twice the Bragg angle, i.e.
Intensity
The amount of light diffracted by the sound wave depends on the intensity of the sound. Hence, the intensity of the sound can be used to modulate the intensity of the light in the diffracted beam. Typically, the intensity that is diffracted into m = 0 order can be varied between 15% and 99% of the input light intensity. Likewise, the intensity of the m = +1 order can be varied between 0% and 80%.
An expression of the efficiency in m = +1 order is:
where the external phase excursion
To obtain the same efficiency for different wavelength, the RF power in the AOM has to be proportional to the square of the wavelength of the optical beam. Note that this formula also tells us that, when we start at a high RF power P, it might be higher than the first peak in the sine squared function, in which case as we increase P, we would settle at the second peak with a very high RF power, leading to overdriving the AOM and potential damage to the crystal or other components. To avoid this problem, one should always start with a very low RF power, and slowly increase it to settle at the first peak.
Note that there are two configurations that satisfies Bragg Condition: If the incident beam's wavevector's component on the sound wave's propagation direction goes against the sound wave, the Bragg diffraction/scattering process will result in the maximum efficiency into m = +1 order, which has a positive frequency shift; However, if the incident beam goes along the sound wave, the maximum diffraction efficiency into m = –1 order is achieved, which has a negative frequency shift.
Frequency
One difference from Bragg diffraction is that the light is scattering from moving planes. A consequence of this is the frequency of the diffracted beam f in order m will be Doppler-shifted by an amount equal to the frequency of the sound wave F.
This frequency shift can be also understood by the fact that energy and momentum (of the photons and phonons) are conserved in the scattering process. A typical frequency shift varies from 27 MHz, for a less-expensive AOM, to 1 GHz, for a state-of-the-art commercial device. In some AOMs, two acoustic waves travel in opposite directions in the material, creating a standing wave. In this case the spectrum of the diffracted beam contains multiple frequency shifts, in any case integer multiples of the frequency of the sound wave.
Phase
In addition, the phase of the diffracted beam will also be shifted by the phase of the sound wave. The phase can be changed by an arbitrary amount.
Polarization
Collinear transverse acoustic waves or perpendicular longitudinal waves can change the polarization. The acoustic waves induce a birefringent phase-shift, much like in a Pockels cell. The acousto-optic tunable filter, especially the dazzler, which can generate variable pulse shapes, is based on this principle.
Mode-locking
Acousto-optic modulators are much faster than typical mechanical devices such as tiltable mirrors. The time it takes an AOM to shift the exiting beam in is roughly limited to the transit time of the sound wave across the beam (typically 5 to 100 ns). This is fast enough to create active modelocking in an ultrafast laser. When faster control is necessary electro-optic modulators are used. However, these require very high voltages (e.g. 1...10 kV), whereas AOMs offer more deflection range, simple design, and low power consumption (less than 3 W).
Applications
- Q-switching
- Regenerative amplifiers
- Cavity dumping
- Modelocking
- Laser Doppler vibrometer
- Film scanner
- Confocal microscopy
- Synthetic array heterodyne detection
- Hyperspectral Imaging
See also
- Acousto-optics
- Acousto-optic deflector
- Acousto-optical spectrometer
- Electro-optic modulator
- Jeffree cell
- Liquid crystal tunable filter
- Photoelasticity
- Pockels effect
References
- "Acousto-optic Theory Application Notes" (PDF).
- Paschotta, Dr Rüdiger. "Acousto-optic Modulators". www.rp-photonics.com. Retrieved 2020-08-03.
- McCarron, D. J. (December 7, 2007). "A Guide to Acousto-Optic Modulators" (PDF). McCarron Group. Retrieved 1 June 2023.
- "A Guide to Acousto-Optic Modulators"
- Lekavich, J. (Apr 1986). "Basics of acousto-optic devices". Lasers and Applications: 59–64.
- Eklund, H.; Roos, A.; Eng, S.T. (1975). "Rotation of laser beam polarization in acousto-optic devices". Optical and Quantum Electronics. 7 (2): 73–79. doi:10.1007/BF00631587. S2CID 122616113.
- Keller, Ursula; Gallmann, Lukas. "Ultrafast Laser Physics" (PDF). ETH Zurich. Retrieved 21 March 2022.
 from the
from the 



