In combinatorial mathematics, Catalan's triangle is a number triangle whose entries give the number of strings consisting of n X's and k Y's such that no initial segment of the string has more Y's than X's. It is a generalization of the Catalan numbers, and is named after Eugène Charles Catalan. Bailey shows that satisfy the following properties:
- .
- .
- .
Formula 3 shows that the entry in the triangle is obtained recursively by adding numbers to the left and above in the triangle. The earliest appearance of the Catalan triangle along with the recursion formula is in page 214 of the treatise on Calculus published in 1800 by Louis François Antoine Arbogast.
Shapiro introduces another triangle which he calls the Catalan triangle that is distinct from the triangle being discussed here.
General formula
The general formula for is given by
So
When , the diagonal C(n, n) is the n-th Catalan number.
The row sum of the n-th row is the (n + 1)-th Catalan number, using the hockey-stick identity and an alternative expression for Catalan numbers.
Table of values
Some values are given by
kn 0 1 2 3 4 5 6 7 8 0 1 1 1 1 2 1 2 2 3 1 3 5 5 4 1 4 9 14 14 5 1 5 14 28 42 42 6 1 6 20 48 90 132 132 7 1 7 27 75 165 297 429 429 8 1 8 35 110 275 572 1001 1430 1430
Properties
- Formula 3 from the first section can be used to prove both
That is, an entry is the partial sum of the above row and also the partial sum of the column to the left (except for the entry on the diagonal).
- If , then at some stage there must be more Y's than X's, so .
- A combinatorial interpretation of the -th value is the number of non-decreasing partitions with exactly n parts with maximum part k such that each part is less than or equal to its index. So, for example, counts
Generalization
Catalan's trapezoids are a countable set of number trapezoids which generalize Catalan’s triangle. Catalan's trapezoid of order m = 1, 2, 3, ... is a number trapezoid whose entries give the number of strings consisting of n X-s and k Y-s such that in every initial segment of the string the number of Y-s does not exceed the number of X-s by m or more. By definition, Catalan's trapezoid of order m = 1 is Catalan's triangle, i.e., .
Some values of Catalan's trapezoid of order m = 2 are given by
kn 0 1 2 3 4 5 6 7 8 0 1 1 1 1 2 2 2 1 3 5 5 3 1 4 9 14 14 4 1 5 14 28 42 42 5 1 6 20 48 90 132 132 6 1 7 27 75 165 297 429 429 7 1 8 35 110 275 572 1001 1430 1430
Some values of Catalan's trapezoid of order m = 3 are given by
kn 0 1 2 3 4 5 6 7 8 9 0 1 1 1 1 1 2 3 3 2 1 3 6 9 9 3 1 4 10 19 28 28 4 1 5 15 34 62 90 90 5 1 6 21 55 117 207 297 297 6 1 7 28 83 200 407 704 1001 1001 7 1 8 36 119 319 726 1430 2431 3432 3432
Again, each element is the sum of the one above and the one to the left.
A general formula for is given by
( n = 0, 1, 2, ..., k = 0, 1, 2, ..., m = 1, 2, 3, ...).
Proofs of the general formula
Proof 1
This proof involves an extension of Andre's reflection method as used in the second proof for the Catalan number to different diagonals. The following shows how every path from the bottom left to the top right of the diagram that crosses the constraint can also be reflected to the end point .
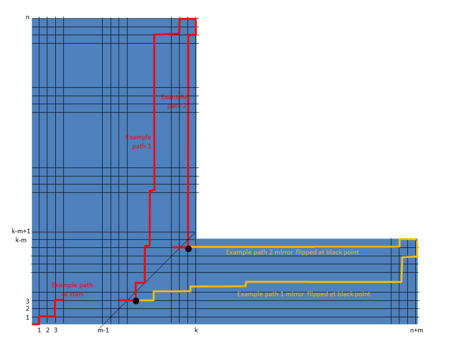
We consider three cases to determine the number of paths from to that do not cross the constraint:
(1) when the constraint cannot be crossed, so all paths from to are valid, i.e. .
(2) when it is impossible to form a path that does not cross the constraint, i.e. .
(3) when , then is the number of 'red' paths minus the number of 'yellow' paths that cross the constraint, i.e. .
Therefore the number of paths from to that do not cross the constraint is as indicated in the formula in the previous section "Generalization".
Proof 2
Firstly, we confirm the validity of the recurrence relation by breaking down into two parts, the first for XY combinations ending in X and the second for those ending in Y. The first group therefore has valid combinations and the second has . Proof 2 is completed by verifying the solution satisfies the recurrence relation and obeys initial conditions for and .
References
- ^ Bailey, D. F. (1996). "Counting Arrangements of 1's and -1's". Mathematics Magazine. 69 (2): 128–131. doi:10.1080/0025570X.1996.11996408.
- Arbogast, L. F. A. (1800). Du Calcul des Derivations. Levrault. p. 214.
- Shapiro, L. W. (1976). "A Catalan Triangle". Discrete Mathematics. 14 (1): 83–90. doi:10.1016/0012-365x(76)90009-1.
- Eric W. Weisstein. "Catalan's Triangle". MathWorld − A Wolfram Web Resource. Retrieved March 28, 2012.
- Sloane, N. J. A. (ed.). "Sequence A009766 (Catalan's triangle)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved March 28, 2012.
- Reuveni, Shlomi (2014). "Catalan's trapezoids". Probability in the Engineering and Informational Sciences. 28 (3): 4391–4396. doi:10.1017/S0269964814000047. S2CID 122765015.
 give the number of strings consisting of n X's and k Y's such that no initial segment of the string has more Y's than X's. It is a generalization of the
give the number of strings consisting of n X's and k Y's such that no initial segment of the string has more Y's than X's. It is a generalization of the  .
. .
.
 .
.

 , the diagonal C(n, n) is the n-th
, the diagonal C(n, n) is the n-th 
 , then at some stage there must be more Y's than X's, so
, then at some stage there must be more Y's than X's, so  .
. -th value is the number of non-decreasing partitions with exactly n parts with maximum part k such that each part is less than or equal to its index. So, for example,
-th value is the number of non-decreasing partitions with exactly n parts with maximum part k such that each part is less than or equal to its index. So, for example,  counts
counts
 give the number of strings consisting of n X-s and k Y-s such that in every initial segment of the string the number of Y-s does not exceed the number of X-s by m or more. By definition, Catalan's trapezoid of order m = 1 is Catalan's triangle, i.e.,
give the number of strings consisting of n X-s and k Y-s such that in every initial segment of the string the number of Y-s does not exceed the number of X-s by m or more. By definition, Catalan's trapezoid of order m = 1 is Catalan's triangle, i.e.,  .
.

 to the top right
to the top right  of the diagram that crosses the constraint
of the diagram that crosses the constraint  can also be reflected to the end point
can also be reflected to the end point  .
.
 the constraint cannot be crossed, so all paths from
the constraint cannot be crossed, so all paths from  .
.
 it is impossible to form a path that does not cross the constraint, i.e.
it is impossible to form a path that does not cross the constraint, i.e.  .
.
 , then
, then  minus the number of 'yellow' paths that cross the constraint, i.e.
minus the number of 'yellow' paths that cross the constraint, i.e.  .
.
 by breaking down
by breaking down  valid combinations and the second has
valid combinations and the second has  . Proof 2 is completed by verifying the solution satisfies the recurrence relation and obeys initial conditions for
. Proof 2 is completed by verifying the solution satisfies the recurrence relation and obeys initial conditions for  and
and  .
.