| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
|
Single-winner methodsSingle vote - plurality methods
|
|
Proportional representationParty-list
|
|
Mixed systemsBy results of combination
By mechanism of combination By ballot type |
|
Paradoxes and pathologiesSpoiler effects
Pathological response Paradoxes of majority rule |
Social and collective choiceImpossibility theorems
Positive results |
|
|
The Schulze method (/ˈʃʊltsə/), also known as the beatpath method, is a single winner ranked-choice voting rule developed by Markus Schulze. The Schulze method is a Condorcet completion method, which means it will elect a majority-preferred candidate if one exists. In other words, if most people rank A above B, A will defeat B (whenever this is possible). Schulze's method breaks cyclic ties by using indirect victories. The idea is that if Alice beats Bob, and Bob beats Charlie, then Alice (indirectly) beats Charlie; this kind of indirect win is called a "beatpath".
For proportional representation, a single transferable vote (STV) variant known as Schulze STV also exists. The Schulze method is used by several organizations including Debian, Ubuntu, Gentoo, Pirate Party political parties and many others. It was also used by Wikimedia prior to their adoption of score voting.
Description of the method

Schulze's method uses ranked ballots with equal ratings allowed. There are two common (equivalent) descriptions of Schulze's method.
Beatpath explanation
The idea behind Schulze's method is that if Alice defeats Bob, and Bob beats Charlie, then Alice "indirectly" defeats Charlie. These chained sequences of "beats" are called 'beatpaths'.
Every beatpath is assigned a particular strength. The strength of a single-step beatpath from Alice to Bob is just the number of voters who rank Alice over Bob. For a longer beatpath, consisting of multiple beats, a beatpath is as strong as its weakest link (i.e. the beat with the smallest number of winning votes).
We say Alice has a "beatpath-win" over Bob if her strongest beatpath to Bob is stronger than all of Bob's strongest beatpaths to Alice. The winner is the candidate who has a beatpath-win over every other candidate.
Markus Schulze proved that this definition of a beatpath-win is transitive: in other words, if Alice has a beatpath-win over Bob, and Bob has a beatpath-win over Charlie, Alice has a beatpath-win over Charlie. As a result, the Schulze method is a Condorcet method, providing a full extension of the majority rule to any set of ballots.
Iterative description
The Schulze winner can also be constructed iteratively, using a defeat-dropping method:
- Draw a directed graph with all the candidates as nodes; label the edges with the number of votes supporting the winner.
- If there is more than one candidate left:
- Check if any candidates are tied (and if so, break the ties by random ballot).
- Eliminate all candidates outside the majority-preferred set.
- Delete the edge closest to being tied.
The winner is the only candidate left at the end of the procedure.
Example
In the following example 45 voters rank 5 candidates.
| Number of voters | Order of preference |
|---|---|
| 5 | ACBED |
| 5 | ADECB |
| 8 | BEDAC |
| 3 | CABED |
| 7 | CAEBD |
| 2 | CBADE |
| 7 | DCEBA |
| 8 | EBADC |
The pairwise preferences have to be computed first. For example, when comparing A and B pairwise, there are 5+5+3+7=20 voters who prefer A to B, and 8+2+7+8=25 voters who prefer B to A. So and . The full set of pairwise preferences is:

| 20 | 26 | 30 | 22 | ||
| 25 | 16 | 33 | 18 | ||
| 19 | 29 | 17 | 24 | ||
| 15 | 12 | 28 | 14 | ||
| 23 | 27 | 21 | 31 |
The cells for d have a light green background if d > d, otherwise the background is light red. There is no undisputed winner by only looking at the pairwise differences here.
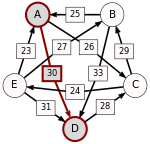
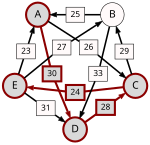
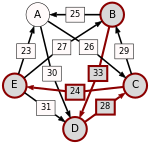
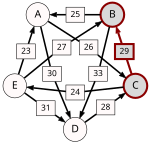
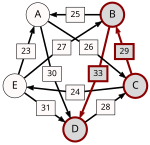
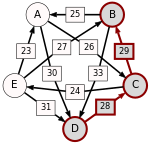
Now the strongest paths have to be identified. To help visualize the strongest paths, the set of pairwise preferences is depicted in the diagram on the right in the form of a directed graph. An arrow from the node representing a candidate X to the one representing a candidate Y is labelled with d. To avoid cluttering the diagram, an arrow has only been drawn from X to Y when d > d (i.e. the table cells with light green background), omitting the one in the opposite direction (the table cells with light red background).
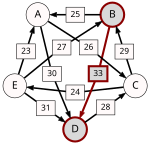
One example of computing the strongest path strength is p = 33: the strongest path from B to D is the direct path (B, D) which has strength 33. But when computing p, the strongest path from A to C is not the direct path (A, C) of strength 26, rather the strongest path is the indirect path (A, D, C) which has strength min(30, 28) = 28. The strength of a path is the strength of its weakest link.
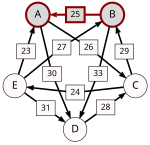
For each pair of candidates X and Y, the following table shows the strongest path from candidate X to candidate Y in red, with the weakest link underlined.
| 28 | 28 | 30 | 24 | ||
| 25 | 28 | 33 | 24 | ||
| 25 | 29 | 29 | 24 | ||
| 25 | 28 | 28 | 24 | ||
| 25 | 28 | 28 | 31 |
Now the output of the Schulze method can be determined. For example, when comparing A and B, since , for the Schulze method candidate A is better than candidate B. Another example is that , so candidate E is better than candidate D. Continuing in this way, the result is that the Schulze ranking is , and E wins. In other words, E wins since for every other candidate X.
Implementation
The only difficult step in implementing the Schulze method is computing the strongest path strengths. However, this is a well-known problem in graph theory sometimes called the widest path problem. One simple way to compute the strengths, therefore, is a variant of the Floyd–Warshall algorithm. The following pseudocode illustrates the algorithm.
# Input: d, the number of voters who prefer candidate i to candidate j.
# Output: p, the strength of the strongest path from candidate i to candidate j.
for i from 1 to C
for j from 1 to C
if i ≠ j then
if d > d then
p := d
else
p := 0
for i from 1 to C
for j from 1 to C
if i ≠ j then
for k from 1 to C
if i ≠ k and j ≠ k then
p := max (p, min (p, p))
This algorithm is efficient and has running time O(C) where C is the number of candidates.
Ties and alternative implementations
When allowing users to have ties in their preferences, the outcome of the Schulze method naturally depends on how these ties are interpreted in defining d. Two natural choices are that d represents either the number of voters who strictly prefer A to B (A>B), or the margin of (voters with A>B) minus (voters with B>A). But no matter how the ds are defined, the Schulze ranking has no cycles, and assuming the ds are unique it has no ties.
Although ties in the Schulze ranking are unlikely, they are possible. Schulze's original paper recommended breaking ties by random ballot.
There is another alternative way to demonstrate the winner of the Schulze method. This method is equivalent to the others described here, but the presentation is optimized for the significance of steps being visually apparent as a human goes through it, not for computation.
- Make the results table, called the "matrix of pairwise preferences", such as used above in the example. Then, every positive number is a pairwise win for the candidate on that row (and marked green), ties are zeroes, and losses are negative (marked red). Order the candidates by how long they last in elimination.
- If there is a candidate with no red on their line, they win.
- Otherwise, draw a square box around the Schwartz set in the upper left corner. It can be described as the minimal "winner's circle" of candidates who do not lose to anyone outside the circle. Note that to the right of the box there is no red, which means it is a winner's circle, and note that within the box there is no reordering possible that would produce a smaller winner's circle.
- Cut away every part of the table outside the box.
- If there is still no candidate with no red on their line, something needs to be compromised on; every candidate lost some race, and the loss we tolerate the best is the one where the loser obtained the most votes. So, take the red cell with the highest number (if going by margins, the least negative), make it green—or any color other than red—and go back step 2.
Here is a margins table made from the above example. Note the change of order used for demonstration purposes.
| E | A | C | B | D | |
|---|---|---|---|---|---|
| E | 1 | −3 | 9 | 17 | |
| A | −1 | 7 | −5 | 15 | |
| C | 3 | −7 | 13 | −11 | |
| B | −9 | 5 | −13 | 21 | |
| D | −17 | −15 | 11 | −21 |
The first drop (A's loss to E by 1 vote) does not help shrink the Schwartz set.
| E | A | C | B | D | |
|---|---|---|---|---|---|
| E | 1 | −3 | 9 | 17 | |
| A | −1 | 7 | −5 | 15 | |
| C | 3 | −7 | 13 | −11 | |
| B | −9 | 5 | −13 | 21 | |
| D | −17 | −15 | 11 | −21 |
So we get straight to the second drop (E's loss to C by 3 votes), and that shows us the winner, E, with its clear row.
| E | A | C | B | D | |
|---|---|---|---|---|---|
| E | 1 | −3 | 9 | 17 | |
| A | −1 | 7 | −5 | 15 | |
| C | 3 | −7 | 13 | −11 | |
| B | −9 | 5 | −13 | 21 | |
| D | −17 | −15 | 11 | −21 |
This method can also be used to calculate a result, if the table is remade in such a way that one can conveniently and reliably rearrange the order of the candidates on both the row and the column, with the same order used on both at all times.
Satisfied and failed criteria
Satisfied criteria
The Schulze method satisfies the following criteria:
- Monotonicity criterion
- Majority criterion
- Majority loser criterion
- Condorcet criterion
- Condorcet loser criterion
- Smith criterion
- Independence of Smith-dominated alternatives
- Mutual majority criterion
- Independence of clones
- Reversal symmetry
- Mono-append
- Mono-add-plump
- Resolvability criterion
- Polynomial runtime
- prudence
- MinMax sets
- Woodall's plurality criterion if winning votes are used for d
- Symmetric-completion if margins are used for d
Failed criteria
Since the Schulze method satisfies the Condorcet criterion, it automatically fails the following criteria:
Likewise, since the Schulze method is not a dictatorship and is a ranked voting system (not rated), Arrow's Theorem implies it fails independence of irrelevant alternatives, meaning it can be vulnerable to the spoiler effect in some rare circumstances. The Schulze method also fails Peyton Young's criterion of Local Independence of Irrelevant Alternatives.
Comparison table
The following table compares the Schulze method with other single-winner election methods:
| Criterion Method |
Majority winner | Majority loser | Mutual majority | Condorcet winner |
Condorcet loser | Smith |
Smith-IIA |
IIA/LIIA |
Cloneproof | Monotone | Participation | Later-no-harm |
Later-no-help |
No favorite betrayal |
Ballot
type | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First-past-the-post voting | Yes | No | No | No | No | No | No | No | No | Yes | Yes | Yes | Yes | No | Single mark | |
| Anti-plurality | No | Yes | No | No | No | No | No | No | No | Yes | Yes | No | No | Yes | Single mark | |
| Two round system | Yes | Yes | No | No | Yes | No | No | No | No | No | No | Yes | Yes | No | Single mark | |
| Instant-runoff | Yes | Yes | Yes | No | Yes | No | No | No | Yes | No | No | Yes | Yes | No | Ranking | |
| Coombs | Yes | Yes | Yes | No | Yes | No | No | No | No | No | No | No | No | Yes | Ranking | |
| Nanson | Yes | Yes | Yes | Yes | Yes | Yes | No | No | No | No | No | No | No | No | Ranking | |
| Baldwin | Yes | Yes | Yes | Yes | Yes | Yes | No | No | No | No | No | No | No | No | Ranking | |
| Tideman alternative | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes | No | No | No | No | No | Ranking | |
| Minimax | Yes | No | No | Yes |
No | No | No | No | No | Yes | No | No |
No | No | Ranking | |
| Copeland | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | No | Yes | No | No | No | No | Ranking | |
| Black | Yes | Yes | No | Yes | Yes | No | No | No | No | Yes | No | No | No | No | Ranking | |
| Kemeny–Young | Yes | Yes | Yes | Yes | Yes | Yes | Yes | LIIA Only | No | Yes | No | No | No | No | Ranking | |
| Ranked pairs | Yes | Yes | Yes | Yes | Yes | Yes | Yes | LIIA Only | Yes | Yes | No |
No | No | No | Ranking | |
| Schulze | Yes | Yes | Yes | Yes | Yes | Yes | Yes | No | Yes | Yes | No |
No | No | No | Ranking | |
| Borda | No | Yes | No | No | Yes | No | No | No | No | Yes | Yes | No | Yes | No | Ranking | |
| Bucklin | Yes | Yes | Yes | No | No | No | No | No | No | Yes | No | No | Yes | No | Ranking | |
| Approval | Yes | No | No | No | No | No | No | Yes |
Yes | Yes | Yes | No | Yes | Yes | Approvals | |
| Majority Judgement | No | No |
No |
No | No | No | No | Yes |
Yes | Yes | No |
No | Yes | Yes | Scores | |
| Score | No | No | No | No | No | No | No | Yes |
Yes | Yes | Yes | No | Yes | Yes | Scores | |
| STAR | No | Yes | No | No | Yes | No | No | No | No | Yes | No | No | No | No | Scores | |
| Quadratic | No | No | No | No | No | No | No | No | No | Yes | Yes | N/A | N/A | No | Credits | |
| Random ballot |
No | No | No | No | No | No | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Single mark | |
| Sortition |
No | No | No | No | No | No | No | Yes | No | Yes | Yes | Yes | Yes | Yes | None | |
| Table Notes |
| |||||||||||||||
Difference from ranked pairs
Ranked pairs is another Condorcet method which is very similar to Schulze's rule, and typically produces the same outcome. There are slight differences, however. The main difference between the beatpath method and ranked pairs is that Schulze retains behavior closer to minimax. Say that the minimax score of a set X of candidates is the strength of the strongest pairwise win of a candidate A ∉ X against a candidate B ∈ X. Then the Schulze method, but not ranked pairs, guarantees the winner is always a candidate of the set with minimum minimax score. This is the sense in which the Schulze method minimizes the largest majority that has to be reversed when determining the winner.
On the other hand, Ranked Pairs minimizes the largest majority that has to be reversed to determine the order of finish. In other words, when Ranked Pairs and the Schulze method produce different orders of finish, for the majorities on which the two orders of finish disagree, the Schulze order reverses a larger majority than the Ranked Pairs order.
History
The Schulze method was developed by Markus Schulze in 1997. It was first discussed in public mailing lists in 1997–1998 and in 2000. In 2011, Schulze published the method in the academic journal Social Choice and Welfare.
Usage

Government
The Schulze method is used by the city of Silla, Spain for all referendums. It is also used by the cities of Turin and San Donà di Piave in Italy and by the London Borough of Southwark through their use of the WeGovNow platform, which in turn uses the LiquidFeedback decision tool.
Political parties
Schulze was adopted by the Pirate Party of Sweden (2009), and the Pirate Party of Germany (2010). The Boise, Idaho chapter of the Democratic Socialists of America in February chose this method for their first special election held in March 2018.
- Five Star Movement of Campobasso, Fondi, Monte Compatri, Montemurlo, Pescara, and San Cesareo
- Pirate Parties of Australia, Austria, Belgium, Brazil, Germany, Iceland, Italy, the Netherlands, Sweden, Switzerland, and the United States
- SustainableUnion
- Volt Europe
Student government and associations
- AEGEE – European Students' Forum
- Club der Ehemaligen der Deutschen SchülerAkademien e. V.
- Associated Student Government at École normale supérieure de Paris
- Flemish Society of Engineering Students Leuven
- Graduate Student Organization at the State University of New York: Computer Science (GSOCS)
- Hillegass Parker House
- Kingman Hall
- Associated Students of Minerva Schools at KGI
- Associated Student Government at Northwestern University
- Associated Student Government at University of Freiburg
- Associated Student Government at the Computer Sciences Department of the University of Kaiserslautern
Organizations
It is used by the Institute of Electrical and Electronics Engineers, by the Association for Computing Machinery, and by USENIX through their use of the HotCRP decision tool.
Organizations which currently use the Schulze method include:
- Annodex Association
- Berufsverband der Kinder- und Jugendärzte [de] (BVKJ)
- BoardGameGeek
- Cloud Foundry Foundation
- County Highpointers
- Dapr
- Debian
- EuroBillTracker
- European Democratic Education Community (EUDEC)
- FFmpeg
- Free Geek
- Free Hardware Foundation of Italy
- Gentoo Foundation
- GNU Privacy Guard (GnuPG)
- Haskell
- Homebrew
- Internet Corporation for Assigned Names and Numbers (ICANN) (until 2023)
- Kanawha Valley Scrabble Club
- KDE e.V.
- Knight Foundation
- Kubernetes
- Kumoricon
- League of Professional System Administrators (LOPSA)
- LiquidFeedback
- Madisonium
- Metalab
- MTV
- Neo
- Noisebridge
- OpenEmbedded
- Open Neural Network Exchange
- OpenStack
- OpenSwitch
- RLLMUK
- Squeak
- Students for Free Culture
- Sugar Labs
- Sverok
- TopCoder
- Ubuntu
- Vidya Gaem Awards
- Wikimedia (2008)
- Misplaced Pages in French, Hebrew, Hungarian, Russian, and Persian.
Notes
- Markus Schulze, "A new monotonic, clone-independent, reversal symmetric, and Condorcet-consistent single-winner election method", Social Choice and Welfare, volume 36, number 2, page 267–303, 2011. Preliminary version in Voting Matters, 17:9-19, 2003.
- ^ Markus Schulze, "A new monotonic, clone-independent, reversal symmetric, and condorcet-consistent single-winner election method", Social Choice and Welfare, volume 36, number 2, page 267–303, 2011. Preliminary version in Voting Matters, 17:9-19, 2003.
- ^ Markus Schulze, "A new monotonic, clone-independent, reversal symmetric, and condorcet-consistent single-winner election method", Social Choice and Welfare, volume 36, number 2, page 267–303, 2011. Preliminary version in Voting Matters, 17:9-19, 2003.
- ^ Douglas R. Woodall, Properties of Preferential Election Rules, Voting Matters, issue 3, pages 8–15, December 1994
- Tideman, T. Nicolaus, "Independence of clones as a criterion for voting rules", Social Choice and Welfare vol 4 #3 (1987), pp. 185–206.
- See:
- Markus Schulze, Condorect sub-cycle rule, October 1997
- Mike Ossipoff, Party List P.S., July 1998
- Markus Schulze, Tiebreakers, Subcycle Rules, August 1998
- Markus Schulze, Maybe Schulze is decisive, August 1998
- Norman Petry, Schulze Method - Simpler Definition, September 1998
- Markus Schulze, Schulze Method, November 1998
- See:
- Anthony Towns, Disambiguation of 4.1.5, November 2000
- Norman Petry, Constitutional voting, definition of cumulative preference, December 2000
- Hortanoticias, Redacción (2016-02-23). "Al voltant de 2.000 participants en dos dies en la primera enquesta popular de Silla que decidirà sobre espectacles taurins". Hortanoticias.com (in Spanish). Retrieved 2022-09-24.
S'utilitzarà el sistema de recompte Schulze perquè és un sistema de vot preferencial que compleix amb el criteri de Condorcet, la qual cosa permet identificar l'opció que, comparada amb qualsevol de les altres, és preferida per la majoria absoluta dels votants
[The Schulze counting system will be used because it is a preferential voting system that complies with the Condorcet criterion, which makes it possible to identify the option that, compared to any other option, is preferred by the absolute majority of voters] - "22-26 de febrer: La primera Enquesta Popular de la història de Silla - Notícies - Ajuntament de Silla". Silla Town Council (in Catalan). 2016-02-23. Archived from the original on 2016-02-23. Retrieved 2024-12-13.
S'utilitzarà el sistema de recompte Schulze perquè és un sistema de vot preferencial que compleix amb el criteri de Condorcet, la qual cosa permet identificar l'opció que, comparada amb qualsevol de les altres, és preferida per la majoria absoluta dels votants.
[The Schulze counting system will be used because it is a preferential voting system that complies with the Condorcet criterion, which makes it possible to identify the option that, compared to any of the others, is preferred by the absolute majority of voters.] - "UN AÑO DE PROFUNDIZACIÓN DEMOCRÁTICA EN SILLA | Silla en Democracia". Silla in Democracy (in Spanish). 2017-03-22. Archived from the original on 2017-03-22. Retrieved 2024-12-13.
Ha sido un rotundo éxito organizativo que repetiremos y que se gestó desde meses antes, desarrollando un know-how propio y siendo pioneros en la aplicación del sistema de recuento Condorcet-Schulze para las preguntas con respuesta de ordenación preferencial. Logramos un récord impresionante de participación que pulverizó todas las marcas existentes en procesos similares en municipios españoles (la media usual ronda el 10% de participación mientras que en Silla alcanzamos el 27%).
[It has been a resounding organizational success that we will repeat, developed over months with our own know-how, and pioneering the application of the Condorcet-Schulze counting system for questions with preferential ranking responses. We achieved an impressive participation record that shattered all existing benchmarks in similar processes in Spanish municipalities (the usual average is around 10% participation, while in Silla, we reached 27%).] - Silla, ~ El Cresol de (2016-05-26). "Un any d'aprofundiment democràtic a Silla". El Cresol de Silla (in Catalan). Retrieved 2022-09-24.
{{cite web}}: CS1 maint: url-status (link) - "LiquidFeedback in London, Turin and San Donà di Piave | Interaktive Demokratie". interaktive-demokratie.org. Retrieved 2024-12-13.
WeGovNow! … is an OpenStreetMap based E-Government solution to be validated and evaluated in London Southwark (UK), Turin (Italy) and San Donà di Piave (Metropolitan City of Venice, Italy)
- "Algorithms for Good (The Liquid Democracy Journal, Issue 7)". liquid-democracy-journal.org. Retrieved 2024-12-13.
To determine the winner from a set of alternatives, LiquidFeedback implements Clone-Proof Schwartz Sequential Dropping, known as the Schulze Method.
- ^ See:
- "Inför primärvalen" [Before the primary elections] (in Swedish). 8 October 2009. Archived from the original on 24 December 2012.
- "Dags att kandidera till riksdagen" [Time to run for the Riksdag] (in Swedish). 17 October 2009. Archived from the original on 23 July 2014.
- "Råresultat primärvalet" [The raw result of the primary election] (in Swedish). 19 January 2010. Archived from the original on 24 December 2012.
- ^ 11 of the 16 regional sections and the federal section of the Pirate Party of Germany are using LiquidFeedback for unbinding internal opinion polls. In 2010/2011, the Pirate Parties of Neukölln (link), Mitte (link), Steglitz-Zehlendorf (link), Lichtenberg (link), and Tempelhof-Schöneberg (link) adopted the Schulze method for its primaries. Furthermore, the Pirate Party of Berlin (in 2011) (link) and the Pirate Party of Regensburg (in 2012) (link) adopted this method for their primaries.
- Chumich, Andrew. "DSA Special Election". Retrieved 2018-02-25.
- Campobasso. Comunali, scattano le primarie a 5 Stelle, February 2014
- Macaro, Mirko (2015-03-03). "Fondi, il punto sui candidati a sindaco. Certezze, novità e colpi di scena". h24 notizie - portale indipendente di news dalla provincia (in Italian). Retrieved 2022-09-24.
- article 25(5) of the bylaws, October 2013
- "MoVimento 5 Stelle - Montemurlo: 2° Step Comunarie di Montemurlo". November 2013. Archived from the original on 2015-04-02. Retrieved 2022-09-24.
- article 12 of the bylaws, January 2015
- Ridefinizione della lista di San Cesareo con Metodo Schulze, February 2014
- "National Congress 2011 Results – Pirate Party Australia". pirateparty.org.au. 18 November 2011. Retrieved 2022-09-24.
- §6(10) of the bylaws
- Article III.3.4 of the Statutory Rules (french, dutch)
- Píratar (2013-10-23). "Schulze aðferðin". Píratar (in Icelandic). Retrieved 2022-09-24.
- Rules adopted on 18 December 2011
- Pontier, Matthijs (2015-01-11). "Verslag ledenraadpleging 4 januari". Piratenpartij Noord Holland (in Dutch). Retrieved 2022-09-24.
- Pankerl, Florian (2010-09-18). "Piratenversammlung der Piratenpartei Schweiz 2010 – Samstag" (in German). Retrieved 2022-09-24.
- article IV section 3 of the bylaws, July 2012
- §10 III of its bylaws, June 2013
- The Board of Directors of Volt Europe in Spain. "Algunas consideraciones sobre en qué grupo estará Volt Europa en el Parlamento Europeo" [Some considerations on which group Volt Europe will join in the European Parliament]. Medium (in Spanish). Archived from the original on 20 August 2024.
- Hajdu, Tekla (2017-09-24). "The Schulze Method – Agora 101". The AEGEEan - AEGEE's online magazine - AEGEE-Europe. Retrieved 2022-09-24.
- Voting Details, January 2021
- Référendum sur la réforme du thurnage, June 2021
- article 57 of the statutory rules
- "User Voting Instructions". Gso.cs.binghamton.edu. Archived from the original on 2013-09-09. Retrieved 2010-05-08.
- "Hillegass-Parker House Bylaws § 5. Elections". Hillegass-Parker House website. Retrieved 4 October 2015.
- See:
- Konglig Datasektionen KTH
- Ka-Ping Yee, Condorcet elections, March 2005
- Ka-Ping Yee, Kingman adopts Condorcet voting, April 2005
- article 9.4.5.h of the charter, November 2017
- Ajith, Van Atta win ASG election, April 2013
- §6 and §7 of its bylaws, May 2014
- §6(6) of the bylaws
- Election of the Annodex Association committee for 2007, February 2007
- §9a of the bylaws, October 2013
- See:
- 2013 Golden Geek Awards - Nominations Open, January 2014
- 2014 Golden Geek Awards - Nominations Open, January 2015
- 2015 Golden Geek Awards - Nominations Open, March 2016
- 2016 Golden Geek Awards - Nominations Open, January 2017
- 2017 Golden Geek Awards - Nominations Open, February 2018
- 2018 Golden Geek Awards - Nominations Open, March 2019
- article 7(e)(iii)(2) of the charter, May 2021
- Adam Helman, Family Affair Voting Scheme - Schulze Method
- Steering and Technical committee, November 2021
- See:
- "Guidance Document". Eudec.org. 2009-11-15. Retrieved 2010-05-08.
- Democratic election of the server admins Archived 2015-10-02 at the Wayback Machine, July 2010
- Voters Guide, September 2011
- Project:Elections
- "CIVS Election Results: GnuPG Logo Vote". 2013-10-03. Archived from the original on 2013-10-03. Retrieved 2022-09-24.
- Haskell Logo Competition, March 2009
- Article 6 Section 2 of the Constitution, February 2021
- section 9.4.7.3 of the Operating Procedures of the Address Council of the Address Supporting Organization (archived from source 2023-06-06)
- "A club by any other name..." Kanawha Valley Scrabble Club. 2009-04-02. Retrieved 2022-09-24.
- section 3.4.1 of the Rules of Procedures for Online Voting
- Knight Foundation awards $5000 to best created-on-the-spot projects, June 2009
- Kubernetes Community, Kubernetes, 2022-09-24, retrieved 2022-09-24
- "Kumoricon – Mascot Contest". Kumoricon. Retrieved 2022-09-24.
- article 8.3 of the bylaws
- The Principles of LiquidFeedback. Berlin: Interaktive Demokratie e. V. 2014. ISBN 978-3-00-044795-2.
- "Madisonium Bylaws - Adopted". Google Docs.
- "Wahlmodus" (in German). Metalab.at. Retrieved 2010-05-08.
- David Chandler, Voting for more than just either-or, MIT Tech Talk, volume 52, number 19, page 2, 12 March 2008
- See:
- Wahlen zum Neo-2-Freeze: Formalitäten Archived 2011-07-27 at the Wayback Machine, February 2010
- Hinweise zur Stimmabgabe, March 2010
- Ergebnisse, March 2010
- "2009 Director Elections". noisebridge.net.
- "Online Voting Policy". openembedded.org.
- ONNX Steering Committee election guideline
- "OpenStack Election — OpenStack Governance". governance.openstack.org. Retrieved 2022-09-24.
- Mark, Atwood (May 25, 2016). "[Partners] text of OpenSwitch Project Charter 2016-05-03". Retrieved 2022-09-24.
- "Committee Elections 2012". rllmuk. 10 April 2012. Retrieved 2022-09-24.
- Squeak Oversight Board Election 2010, March 2010
- See:
- Bylaws of the Students for Free Culture Archived 2013-03-18 at the Wayback Machine, article V, section 1.1.1
- Free Culture Student Board Elected Using Selectricity, February 2008
- "[IAEP] Election status update". lists.sugarlabs.org. Retrieved 2022-09-24.
- Minutes of the 2018 Annual Sverok Meeting, November 2018
- "2007 TopCoder Collegiate Challenge". community.topcoder.com. Retrieved 2022-09-24.
- Bell, Alan (May 17, 2012). "Ubuntu IRC Council Position". Retrieved 2022-09-24.
- "/v/GAs - Pairwise voting results". vidyagaemawards.com.
- See:
- 2008 Board Elections, June 2008
- 2009 Board Elections, August 2009
- 2011 Board Elections, June 2011
- "Wikipédia:Prise de décision/Choix dans les votes", Wikipédia (in French), 2019-08-22, retrieved 2022-09-24
- "ויקיפדיה:פרלמנט/הכרעה" [Misplaced Pages:Parliament/Decisionmaking]. he.wikipedia.org (in Hebrew).
- See e.g. here (May 2009), here (August 2009), and here (December 2009).
- See here and here.
- Девятнадцатые выборы арбитров, второй тур [Result of Arbitration Committee Elections]. kalan.cc (in Russian). Archived from the original on 2015-02-22.
- See here
External links
- The Schulze Method of Voting by Markus Schulze
- The Schulze Method by Hubert Bray
- Spieltheorie (in German) by Bernhard Nebel
- Accurate Democracy by Rob Loring
- Christoph Börgers (2009), Mathematics of Social Choice: Voting, Compensation, and Division, SIAM, ISBN 0-89871-695-0
- Nicolaus Tideman (2006), Collective Decisions and Voting: The Potential for Public Choice, Burlington: Ashgate, ISBN 0-7546-4717-X
- preftools by the Public Software Group
- Arizonans for Condorcet Ranked Voting
- Condorcet PHP Command line application and PHP library, supporting multiple Condorcet methods, including Schulze.
- Implementation in Java
- Implementation in Ruby
- Implementation in Python 2
- Implementation in Python 3
 and
and  . The full set of pairwise preferences is:
. The full set of pairwise preferences is:





















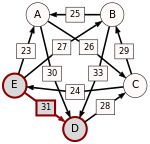










 , for the Schulze method candidate A is better than candidate B. Another example is that
, for the Schulze method candidate A is better than candidate B. Another example is that  , so candidate E is better than candidate D. Continuing in this way, the result is that the Schulze ranking is
, so candidate E is better than candidate D. Continuing in this way, the result is that the Schulze ranking is  , and E wins. In other words, E wins since
, and E wins. In other words, E wins since  for every other candidate X.
for every other candidate X.