| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Economic equilibrium" – news · newspapers · books · scholar · JSTOR (April 2020) (Learn how and when to remove this message) |
In economics, economic equilibrium is a situation in which the economic forces of supply and demand are balanced, meaning that economic variables will no longer change.
Market equilibrium in this case is a condition where a market price is established through competition such that the amount of goods or services sought by buyers is equal to the amount of goods or services produced by sellers. This price is often called the competitive price or market clearing price and will tend not to change unless demand or supply changes, and quantity is called the "competitive quantity" or market clearing quantity.
Understanding economic equilibrium
An economic equilibrium is a situation when the economic agent cannot change the situation by adopting any strategy. The concept has been borrowed from the physical sciences. Take a system where physical forces are balanced for instance.This economically interpreted means no further change ensues.
Properties of equilibrium
Three basic properties of equilibrium in general have been proposed by Huw Dixon. These are:
- Equilibrium property P1: The behavior of agents is consistent.
- Equilibrium property P2: No agent has an incentive to change its behavior.
- Equilibrium property P3: Equilibrium is the outcome of some dynamic process (stability).
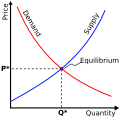
Example: competitive equilibrium

- P – price
- Q – quantity demanded and supplied
- S – supply curve
- D – demand curve
- P0 – equilibrium price
- A – excess demand – when P<P0
- B – excess supply – when P>P0
In a competitive equilibrium, supply equals demand. Property P1 is satisfied, because at the equilibrium price the amount supplied is equal to the amount demanded. Property P2 is also satisfied. Demand is chosen to maximize utility given the market price: no one on the demand side has any incentive to demand more or less at the prevailing price. Likewise supply is determined by firms maximizing their profits at the market price: no firm will want to supply any more or less at the equilibrium price. Hence, agents on neither the demand side nor the supply side will have any incentive to alter their actions.
To see whether Property P3 is satisfied, consider what happens when the price is above the equilibrium. In this case there is an excess supply, with the quantity supplied exceeding that demanded. This will tend to put downward pressure on the price to make it return to equilibrium. Likewise where the price is below the equilibrium point (also known as the "sweet spot") there is a shortage in supply leading to an increase in prices back to equilibrium. Not all equilibria are "stable" in the sense of equilibrium property P3. It is possible to have competitive equilibria that are unstable. However, if an equilibrium is unstable, it raises the question of reaching it. Even if it satisfies properties P1 and P2, the absence of P3 means that the market can only be in the unstable equilibrium if it starts off there.
In most simple microeconomic stories of supply and demand a static equilibrium is observed in a market; however, economic equilibrium can be also dynamic. Equilibrium may also be economy-wide or general, as opposed to the partial equilibrium of a single market. Equilibrium can change if there is a change in demand or supply conditions. For example, an increase in supply will disrupt the equilibrium, leading to lower prices. Eventually, a new equilibrium will be attained in most markets. Then, there will be no change in price or the amount of output bought and sold — until there is an exogenous shift in supply or demand (such as changes in technology or tastes). That is, there are no endogenous forces leading to the price or the quantity.
Example: monopolist equilibrium
In a monopoly, marginal revenue (MR) equals marginal cost (MC). The equilibrium quantity is obtained from where MR and MC intersect and the equilibrium price can be found on the demand curve where MR = MC. Property P1 is not satisfied because the amount demand and the amount supplied at the equilibrium price are not equal. Property P2 is not satisfied. Because the monopolist's profit-maximizing quantity is different from the socially-maximizing quantity, consumers have an incentive to demand more at the equilibrium price. However, at the market price, monopolists maximize their profits so they have no incentive to change their price. Therefore, agents on the demand side have an incentive to alter their actions while the agents on the supply side do not have any incentive to alter their actions.
In order to determine if Property P3 is satisfied, the same situations used to determine P3 in a competitive equilibrium can be used. When there is an excess in supply, monopolists will realize that the equilibrium is not at the profit-maximizing quantity and will put upward pressure on the price to make it return to equilibrium. This is the same case when the price is above the equilibrium and the shortage in supply leads the monopolist to decrease the supply to return to the profit-maximizing quantity. Therefore the equilibrium is the result of stability.
Example: Nash equilibrium
Further information: Nash equilibrium and Cournot model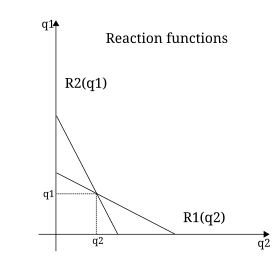
The Nash equilibrium is widely used in economics as the main alternative to competitive equilibrium. It is used whenever there is a strategic element to the behavior of agents and the "price taking" assumption of competitive equilibrium is inappropriate. The first use of the Nash equilibrium was in the Cournot duopoly as developed by Antoine Augustin Cournot in his 1838 book. Both firms produce a homogenous product: given the total amount supplied by the two firms, the (single) industry price is determined using the demand curve. This determines the revenues of each firm (the industry price times the quantity supplied by the firm). The profit of each firm is then this revenue minus the cost of producing the output. Clearly, there is a strategic interdependence between the two firms. If one firm varies its output, this will in turn affect the market price and so the revenue and profits of the other firm. We can define the payoff function which gives the profit of each firm as a function of the two outputs chosen by the firms. Cournot assumed that each firm chooses its own output to maximize its profits given the output of the other firm. The Nash equilibrium occurs when both firms are producing the outputs which maximize their own profit given the output of the other firm.
In terms of the equilibrium properties, we can see that P2 is satisfied: in a Nash equilibrium, neither firm has an incentive to deviate from the Nash equilibrium given the output of the other firm. P1 is satisfied since the payoff function ensures that the market price is consistent with the outputs supplied and that each firms profits equal revenue minus cost at this output.
Is the equilibrium stable as required by P3? Cournot himself argued that it was stable using the stability concept implied by best response dynamics. The reaction function for each firm gives the output which maximizes profits (best response) in terms of output for a firm in terms of a given output of the other firm. In the standard Cournot model this is downward sloping: if the other firm produces a higher output, the best response involves producing less. Best response dynamics involves firms starting from some arbitrary position and then adjusting output to their best-response to the previous output of the other firm. So long as the reaction functions have a slope of less than -1, this will converge to the Nash equilibrium. However, this stability story is open to much criticism. As Dixon argues: "The crucial weakness is that, at each step, the firms behave myopically: they choose their output to maximize their current profits given the output of the other firm, but ignore the fact that the process specifies that the other firm will adjust its output...". There are other concepts of stability that have been put forward for the Nash equilibrium, evolutionary stability for example.
Market clearing prices
Most economists, for example Paul Samuelson, caution against attaching a normative meaning (value judgement) to the equilibrium price. For example, food markets may be in equilibrium at the same time that people are starving (because they cannot afford to pay the high equilibrium price).
Indeed, this occurred during the Great Famine in Ireland in 1845–52, where food was exported though people were starving, due to the greater profits in selling to the English – the equilibrium price of the Irish-British market for potatoes was above the price that Irish farmers could afford, and thus (among other reasons) they starved.
Interpretations
In most interpretations, classical economists such as Adam Smith maintained that the free market would tend towards economic equilibrium through the price mechanism. That is, any excess supply (market surplus or glut) would lead to price cuts, which decrease the quantity supplied (by reducing the incentive to produce and sell the product) and increase the quantity demanded (by offering consumers bargains), automatically abolishing the glut. Similarly, in an unfettered market, any excess demand (or shortage) would lead to price increases, reducing the quantity demanded (as customers are priced out of the market) and increasing in the quantity supplied (as the incentive to produce and sell a product rises). As before, the disequilibrium (here, the shortage) disappears. This automatic abolition of non-market-clearing situations distinguishes markets from central planning schemes, which often have a difficult time getting prices right and suffer from persistent shortages of goods and services.
This view came under attack from at least two viewpoints. Modern mainstream economics points to cases where equilibrium does not correspond to market clearing (but instead to unemployment), as with the efficiency wage hypothesis in labor economics. In some ways parallel is the phenomenon of credit rationing, in which banks hold interest rates low to create an excess demand for loans, so they can pick and choose whom to lend to. Further, economic equilibrium can correspond with monopoly, where the monopolistic firm maintains an artificial shortage to prop up prices and to maximize profits. Finally, Keynesian macroeconomics points to underemployment equilibrium, where a surplus of labor (i.e., cyclical unemployment) co-exists for a long time with a shortage of aggregate demand.
Solving for the competitive equilibrium price
To find the equilibrium price, one must either plot the supply and demand curves, or solve for the expressions for supply and demand being equal.
An example may be:

In the diagram, depicting simple set of supply and demand curves, the quantity demanded and supplied at price P are equal.
At any price above P supply exceeds demand, while at a price below P the quantity demanded exceeds that supplied. In other words, prices where demand and supply are out of balance are termed points of disequilibrium, creating shortages and oversupply. Changes in the conditions of demand or supply will shift the demand or supply curves. This will cause changes in the equilibrium price and quantity in the market.
Consider the following demand and supply schedule:
| Price ($) | Demand | Supply |
|---|---|---|
| 8.00 | 6,000 | 18,000 |
| 7.00 | 8,000 | 16,000 |
| 6.00 | 10,000 | 14,000 |
| 5.00 | 12,000 | 12,000 |
| 4.00 | 14,000 | 10,000 |
| 3.00 | 16,000 | 8,000 |
| 2.00 | 18,000 | 6,000 |
| 1.00 | 20,000 | 4,000 |
- The equilibrium price in the market is $5.00 where demand and supply are equal at 12,000 units
- If the current market price was $3.00 – there would be excess demand for 8,000 units, creating a shortage.
- If the current market price was $8.00 – there would be excess supply of 12,000 units.
When there is a shortage in the market we see that, to correct this disequilibrium, the price of the good will be increased back to a price of $5.00, thus lessening the quantity demanded and increasing the quantity supplied thus that the market is in balance.
When there is an oversupply of a good, such as when price is above $6.00, then we see that producers will decrease the price to increase the quantity demanded for the good, thus eliminating the excess and taking the market back to equilibrium.
Influences changing price
A change in equilibrium price may occur through a change in either the supply or demand schedules. For instance, starting from the above supply-demand configuration, an increased level of disposable income may produce a new demand schedule, such as the following:
| Price ($) | Demand | Supply |
|---|---|---|
| 8.00 | 10,000 | 18,000 |
| 7.00 | 12,000 | 16,000 |
| 6.00 | 14,000 | 14,000 |
| 5.00 | 16,000 | 12,000 |
| 4.00 | 18,000 | 10,000 |
| 3.00 | 20,000 | 8,000 |
| 2.00 | 22,000 | 6,000 |
| 1.00 | 24,000 | 4,000 |
Here we see that an increase in disposable income would increase the quantity demanded of the good by 2,000 units at each price. This increase in demand would have the effect of shifting the demand curve rightward. The result is a change in the price at which quantity supplied equals quantity demanded. In this case we see that the two now equal each other at an increased price of $6.00. A decrease in disposable income would have the exact opposite effect on the market equilibrium.
We will also see similar behaviour in price when there is a change in the supply schedule, occurring through technological changes, or through changes in business costs. An increase in technological usage or know-how or a decrease in costs would have the effect of increasing the quantity supplied at each price, thus reducing the equilibrium price. On the other hand, a decrease in technology or increase in business costs will decrease the quantity supplied at each price, thus increasing equilibrium price.
The process of comparing two static equilibria to each other, as in the above example, is known as comparative statics. For example, since a rise in consumers' income leads to a higher price (and a decline in consumers' income leads to a fall in the price — in each case the two things change in the same direction), we say that the comparative static effect of consumer income on the price is positive. This is another way of saying that the total derivative of price with respect to consumer income is greater than zero.
Dynamic equilibrium
Whereas in a static equilibrium all quantities have unchanging values, in a dynamic equilibrium various quantities may all be growing at the same rate, leaving their ratios unchanging. For example, in the neoclassical growth model, the working population is growing at a rate which is exogenous (determined outside the model, by non-economic forces). In dynamic equilibrium, output and the physical capital stock also grow at that same rate, with output per worker and the capital stock per worker unchanging. Similarly, in models of inflation a dynamic equilibrium would involve the price level, the nominal money supply, nominal wage rates, and all other nominal values growing at a single common rate, while all real values are unchanging, as is the inflation rate.
The process of comparing two dynamic equilibria to each other is known as comparative dynamics. For example, in the neoclassical growth model, starting from one dynamic equilibrium based in part on one particular saving rate, a permanent increase in the saving rate leads to a new dynamic equilibrium in which there are permanently higher capital per worker and productivity per worker, but an unchanged growth rate of output; so it is said that in this model the comparative dynamic effect of the saving rate on capital per worker is positive but the comparative dynamic effect of the saving rate on the output growth rate is zero.
Disequilibrium
Main article: Disequilibrium macroeconomics § Specific economic sectorsDisequilibrium characterizes a market that is not in equilibrium. Disequilibrium can occur extremely briefly or over an extended period of time. At the other extreme, many economists view labor markets as being in a state of disequilibrium—specifically one of excess supply—over extended periods of time. Goods markets are somewhere in between: prices of some goods, while sluggish in adjusting due to menu costs, long-term contracts, and other impediments, do not stay at disequilibrium levels indefinitely.
See also
- Exchange value
- Labor theory of value
- Law of value
- General equilibrium theory
- Prices of production
- Real prices and ideal prices
- Asset pricing#General equilibrium asset pricing
References
- Varian, Hal R. (1992). Microeconomic Analysis (Third ed.). New York: Norton. ISBN 0-393-95735-7.
- Dixon, H. (1990). "Equilibrium and Explanation". In Creedy (ed.). The Foundations of Economic Thought. Blackwells. pp. 356–394. ISBN 0-631-15642-9. (reprinted in Surfing Economics).
- Finding the sweet spot: how to get the right staffing for variable workloads Bryce, Christensen; Healthcare Financial Management 2011 Mar;65(3):54-60
- Augustin Cournot (1838), Theorie mathematique de la richesse sociale and of recherches sur les principles mathematiques de la theorie des richesses, Paris
- Dixon (1990), page 369.
- Paul A. Samuelson (1947; Expanded ed. 1983), Foundations of Economic Analysis , Harvard University Press. ISBN 0-674-31301-1
- See citations at Great Famine (Ireland): Food exports to England, including Cecil Woodham-Smith The Great Hunger; Ireland 1845–1849, and Christine Kinealy, 'Irish Famine: This Great Calamity and A Death-Dealing Famine'
- Smith, Adam (1776), Wealth of Nations Archived 2013-10-20 at the Wayback Machine, Penn State Electronic Classics edition, republished 2005, Chapter 7: p.51-58
- Turnovsky, Stephen J. (2000). Methods of Macroeconomic Dynamics. MIT Press. ISBN 0-262-20123-2.
- O'Sullivan, Arthur; Sheffrin, Steven M. (2003). Economics: Principles in Action. Upper Saddle River, New Jersey: Pearson Prentice Hall. p. 550. ISBN 0-13-063085-3.
External links
- Equilibrium and Explanation, chapter 2 of Surfing Economics by Huw Dixon
| Population | |
|---|---|
| Major topics | |
| Population biology | |
| Population ecology | |
| Society and population | |
| Publications | |
| Lists | |
| Events and organizations |
|
| Related topics | |