| The topic of this article may not meet Misplaced Pages's notability guideline for numbers. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the article is likely to be merged, redirected, or deleted. Find sources: "Compound of five octahemioctahedra" – news · newspapers · books · scholar · JSTOR (July 2019) (Learn how and when to remove this message) |
| Compound of five octahemioctahedra | |
|---|---|
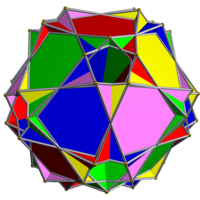
| |
| Type | Uniform compound |
| Index | UC61 |
| Polyhedra | 5 octahemioctahedra |
| Faces | 40 triangles, 20 hexagons |
| Edges | 120 |
| Vertices | 60 |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
In geometry, this uniform polyhedron compound is a composition of 5 octahemioctahedra, in the same vertex arrangement as in the compound of 5 cuboctahedra.
Filling
There is some controversy on how to colour the faces of this polyhedron compound. Although the common way to fill in a polygon is to just colour its whole interior, this can result in some filled regions hanging as membranes over empty space. Hence, the "neo filling" is sometimes used instead as a more accurate filling. In the neo filling, orientable polyhedra are filled traditionally, but non-orientable polyhedra have their faces filled with the modulo-2 method (only odd-density regions are filled in). In addition, overlapping regions of coplanar faces can cancel each other out. Usage of the "neo filling" makes the compound of five octahemioctahedra a hollow polyhedron compound.
 Traditional filling |
 "Neo filling" |
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, Bibcode:1976MPCPS..79..447S, doi:10.1017/S0305004100052440, MR 0397554, S2CID 123279687.