The Fibonacci word fractal is a fractal curve defined on the plane from the Fibonacci word.
Definition


This curve is built iteratively by applying the Odd–Even Drawing rule to the Fibonacci word 0100101001001...:
For each digit at position k:
- If the digit is 0:
- If the digit is 1:
- Draw a line segment and stay straight
To a Fibonacci word of length (the n Fibonacci number) is associated a curve made of segments. The curve displays three different aspects whether n is in the form 3k, 3k + 1, or 3k + 2.
Properties

Some of the Fibonacci word fractal's properties include:
- The curve contains segments, right angles and flat angles.
- The curve never self-intersects and does not contain double points. At the limit, it contains an infinity of points asymptotically close.
- The curve presents self-similarities at all scales. The reduction ratio is . This number, also called the silver ratio, is present in a great number of properties listed below.
- The number of self-similarities at level n is a Fibonacci number \ −1. (more precisely: ).
- The curve encloses an infinity of square structures of decreasing sizes in a ratio (see figure). The number of those square structures is a Fibonacci number.
- The curve can also be constructed in different ways (see gallery below):
- Iterated function system of 4 and 1 homothety of ratio and
- By joining together the curves and
- Lindenmayer system
- By an iterated construction of 8 square patterns around each square pattern.
- By an iterated construction of octagons
- The Hausdorff dimension of the Fibonacci word fractal is , with the golden ratio.
- Generalizing to an angle between 0 and , its Hausdorff dimension is , with .
- The Hausdorff dimension of its frontier is .
- Exchanging the roles of "0" and "1" in the Fibonacci word, or in the drawing rule yields a similar curve, but oriented 45°.
- From the Fibonacci word, one can define the «dense Fibonacci word», on an alphabet of 3 letters: 102210221102110211022102211021102110221022102211021... (sequence A143667 in the OEIS). The usage, on this word, of a more simple drawing rule, defines an infinite set of variants of the curve, among which:
- a "diagonal variant"
- a "svastika variant"
- a "compact variant"
- It is conjectured that the Fibonacci word fractal appears for every sturmian word for which the slope, written in continued fraction expansion, ends with an infinite sequence of "1"s.
Gallery
-
 Curve after iterations.
Curve after iterations.
-
 Self-similarities at different scales.
Self-similarities at different scales.
-
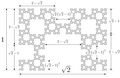 Dimensions.
Dimensions.
-
 Construction by juxtaposition (1)
Construction by juxtaposition (1)
-
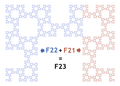 Construction by juxtaposition (2)
Construction by juxtaposition (2)
-
 Order 18, with some sub-rectangles colored.
Order 18, with some sub-rectangles colored.
-

-
 Construction by iterated suppression of square patterns.
Construction by iterated suppression of square patterns.
-
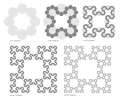 Construction by iterated octagons.
Construction by iterated octagons.
-
 Construction by iterated collection of 8 square patterns around each square pattern.
Construction by iterated collection of 8 square patterns around each square pattern.
-
 With a 60° angle.
With a 60° angle.
-
 Inversion of "0" and "1".
Inversion of "0" and "1".
-
 Variants generated from the dense Fibonacci word.
Variants generated from the dense Fibonacci word.
-
 The "compact variant"
The "compact variant"
-
 The "svastika variant"
The "svastika variant"
-
 The "diagonal variant"
The "diagonal variant"
-
 The "π/8 variant"
The "π/8 variant"
-
 Artist creation (Samuel Monnier).
Artist creation (Samuel Monnier).
The Fibonacci tile

The juxtaposition of four curves allows the construction of a closed curve enclosing a surface whose area is not null. This curve is called a "Fibonacci tile".
- The Fibonacci tile almost tiles the plane. The juxtaposition of 4 tiles (see illustration) leaves at the center a free square whose area tends to zero as k tends to infinity. At the limit, the infinite Fibonacci tile tiles the plane.
- If the tile is enclosed in a square of side 1, then its area tends to .

Fibonacci snowflake

The Fibonacci snowflake is a Fibonacci tile defined by:
- if
- otherwise.
with and , "turn left" and "turn right", and .
Several remarkable properties:
- It is the Fibonacci tile associated to the "diagonal variant" previously defined.
- It tiles the plane at any order.
- It tiles the plane by translation in two different ways.
- its perimeter at order n equals , where is the n Fibonacci number.
- its area at order n follows the successive indexes of odd row of the Pell sequence (defined by ).
See also
References
- Ramírez, José L.; Rubiano, Gustavo N. (2014). "Properties and Generalizations of the Fibonacci Word Fractal", The Mathematical Journal, Vol. 16.
- Monnerot-Dumaine, Alexis (February 2009). "The Fibonacci word fractal", independent (hal.archives-ouvertes.fr).
- Hoffman, Tyler; Steinhurst, Benjamin (2016). "Hausdorff Dimension of Generalized Fibonacci Word Fractals". arXiv:1601.04786 .
- Ramírez, Rubiano, and De Castro (2014). "A generalization of the Fibonacci word fractal and the Fibonacci snowflake", Theoretical Computer Science, Vol. 528, p.40-56.
- ^ Blondin-Massé, Alexandre; Brlek, Srečko; Garon, Ariane; and Labbé, Sébastien (2009). "Christoffel and Fibonacci tiles", Lecture Notes in Computer Science: Discrete Geometry for Computer Imagery, p.67-8. Springer. ISBN 9783642043963.
- A. Blondin-Massé, S. Labbé, S. Brlek, M. Mendès-France (2011). "Fibonacci snowflakes".
External links
- "Generate a Fibonacci word fractal", OnlineMathTools.com.
| Fractals | |
|---|---|
| Characteristics | |
| Iterated function system | |
| Strange attractor | |
| L-system | |
| Escape-time fractals | |
| Rendering techniques | |
| Random fractals | |
| People | |
| Other |
|
 (the n
(the n  made of
made of  contains
contains  right angles and
right angles and  flat angles.
flat angles. . This number, also called the
. This number, also called the  ).
). and
and 
 and
and 
 , with
, with  the
the  between 0 and
between 0 and  , its Hausdorff dimension is
, its Hausdorff dimension is  , with
, with  .
. .
. iterations.
iterations.
 curves allows the construction of a closed curve enclosing a surface whose
curves allows the construction of a closed curve enclosing a surface whose  .
. ,
,  ,
,  ,
, 
 if
if 
 otherwise.
otherwise. and
and  ,
,  "turn left" and
"turn left" and  "turn right", and
"turn right", and  .
.
 , where
, where  is the n
is the n  ).
).