| Frucht graph | |
|---|---|
 The Frucht graph The Frucht graph | |
| Named after | Robert Frucht |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 4 |
| Girth | 3 |
| Automorphisms | 1 ({id}) |
| Chromatic number | 3 |
| Chromatic index | 3 |
| Properties | Cubic Halin Pancyclic |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Frucht graph is a cubic graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.
The Frucht graph is a pancyclic, Halin graph with chromatic number 3, chromatic index 3, radius 3, and diameter 4. Like every Halin graph, the Frucht graph is polyhedral (planar and 3-vertex-connected) and Hamiltonian, with girth 3. Its independence number is 5.
The Frucht graph can be constructed from the LCF notation: .
Algebraic properties
The Frucht graph is one of the five smallest cubic graphs possessing only a single graph automorphism, the identity (that is, every vertex can be distinguished topologically from every other vertex). Such graphs are called asymmetric (or identity) graphs. Frucht's theorem states that any group can be realized as the group of symmetries of a graph, and a strengthening of this theorem also due to Frucht states that any group can be realized as the symmetries of a 3-regular graph; the Frucht graph provides an example of this realization for the trivial group.
The characteristic polynomial of the Frucht graph is .
Gallery
-
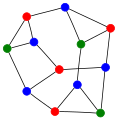 The chromatic number of the Frucht graph is 3.
The chromatic number of the Frucht graph is 3.
-
 The Frucht graph is Hamiltonian.
The Frucht graph is Hamiltonian.
See also
References
- Weisstein, Eric W., "Frucht Graph", MathWorld
- ^ Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe.", Compositio Mathematica (in German), 6: 239–250, ISSN 0010-437X, Zbl 0020.07804.
- Bussemaker, F. C.; Cobeljic, S.; Cvetkovic, D. M.; Seidel, J. J. (1976), Computer investigation of cubic graphs, EUT report, vol. 76-WSK-01, Dept. of Mathematics and Computing Science, Eindhoven University of Technology
- Frucht, R. (1949), "Graphs of degree three with a given abstract group", Canadian Journal of Mathematics, 1 (4): 365–378, doi:10.4153/CJM-1949-033-6, ISSN 0008-414X, MR 0032987, S2CID 124723321.
 .
.