
In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.
1-factorization
If a graph is 1-factorable then it has to be a regular graph. However, not all regular graphs are 1-factorable. A k-regular graph is 1-factorable if it has chromatic index k; examples of such graphs include:
- Any regular bipartite graph. Hall's marriage theorem can be used to show that a k-regular bipartite graph contains a perfect matching. One can then remove the perfect matching to obtain a (k − 1)-regular bipartite graph, and apply the same reasoning repeatedly.
- Any complete graph with an even number of nodes (see below).
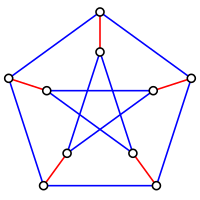
However, there are also k-regular graphs that have chromatic index k + 1, and these graphs are not 1-factorable; examples of such graphs include:
- Any regular graph with an odd number of nodes.
- The Petersen graph.
Complete graphs
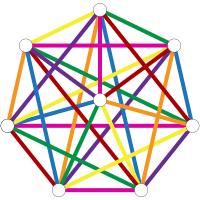
A 1-factorization of a complete graph corresponds to pairings in a round-robin tournament. The 1-factorization of complete graphs is a special case of Baranyai's theorem concerning the 1-factorization of complete hypergraphs.
One method for constructing a 1-factorization of a complete graph on an even number of vertices involves placing all but one of the vertices in a regular polygon, with the remaining vertex at the center. With this arrangement of vertices, one way of constructing a 1-factor of the graph is to choose an edge e from the center to a single polygon vertex together with all possible edges that lie on lines perpendicular to e. The 1-factors that can be constructed in this way form a 1-factorization of the graph.
The number of distinct 1-factorizations of K2, K4, K6, K8, ... is 1, 1, 6, 6240, 1225566720, 252282619805368320, 98758655816833727741338583040, ... (OEIS: A000438).
1-factorization conjecture
Let G be a k-regular graph with 2n nodes. If k is sufficiently large, it is known that G has to be 1-factorable:
- If k = 2n − 1, then G is the complete graph K2n, and hence 1-factorable (see above).
- If k = 2n − 2, then G can be constructed by removing a perfect matching from K2n. Again, G is 1-factorable.
- Chetwynd & Hilton (1985) show that if k ≥ 12n/7, then G is 1-factorable.
The 1-factorization conjecture is a long-standing conjecture that states that k ≈ n is sufficient. In precise terms, the conjecture is:
- If n is odd and k ≥ n, then G is 1-factorable. If n is even and k ≥ n − 1 then G is 1-factorable.
The overfull conjecture implies the 1-factorization conjecture.
Perfect 1-factorization
A perfect pair from a 1-factorization is a pair of 1-factors whose union induces a Hamiltonian cycle.
A perfect 1-factorization (P1F) of a graph is a 1-factorization having the property that every pair of 1-factors is a perfect pair. A perfect 1-factorization should not be confused with a perfect matching (also called a 1-factor).
In 1964, Anton Kotzig conjectured that every complete graph K2n where n ≥ 2 has a perfect 1-factorization. So far, it is known that the following graphs have a perfect 1-factorization:
- the infinite family of complete graphs K2p where p is an odd prime (by Anderson and also Nakamura, independently),
- the infinite family of complete graphs Kp+1 where p is an odd prime,
- and sporadic additional results, including K2n where 2n ∈ {16, 28, 36, 40, 50, 126, 170, 244, 344, 730, 1332, 1370, 1850, 2198, 3126, 6860, 12168, 16808, 29792}. Some newer results are collected here.
If the complete graph Kn+1 has a perfect 1-factorization, then the complete bipartite graph Kn,n also has a perfect 1-factorization.
2-factorization
If a graph is 2-factorable, then it has to be 2k-regular for some integer k. Julius Petersen showed in 1891 that this necessary condition is also sufficient: any 2k-regular graph is 2-factorable.
If a connected graph is 2k-regular and has an even number of edges it may also be k-factored, by choosing each of the two factors to be an alternating subset of the edges of an Euler tour. This applies only to connected graphs; disconnected counterexamples include disjoint unions of odd cycles, or of copies of K2k +1.
The Oberwolfach problem concerns the existence of 2-factorizations of complete graphs into isomorphic subgraphs. It asks for which subgraphs this is possible. This is known when the subgraph is connected (in which case it is a Hamiltonian cycle and this special case is the problem of Hamiltonian decomposition) but the general case remains open.
References
- Harary (1969), Theorem 9.2, p. 85. Diestel (2005), Corollary 2.1.3, p. 37.
- Harary (1969), Theorem 9.1, p. 85.
- Chetwynd & Hilton (1985). Niessen (1994). Perkovic & Reed (1997). West.
- Wallis, W. D. (1997), "16. Perfect Factorizations", One-factorizations, Mathematics and Its Applications, vol. 390 (1 ed.), Springer US, p. 125, doi:10.1007/978-1-4757-2564-3_16, ISBN 978-0-7923-4323-3
- Bryant, Darryn; Maenhaut, Barbara M.; Wanless, Ian M. (May 2002), "A Family of Perfect Factorisations of Complete Bipartite Graphs", Journal of Combinatorial Theory, A, 98 (2): 328–342, doi:10.1006/jcta.2001.3240, ISSN 0097-3165
- Petersen (1891), §9, p. 200. Harary (1969), Theorem 9.9, p. 90. See Diestel (2005), Corollary 2.1.5, p. 39 for a proof.
- Petersen (1891), §6, p. 198.
Bibliography
- Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, archived from the original on 2010-04-13, retrieved 2019-12-18, Section 5.1: "Matchings".
- Chetwynd, A. G.; Hilton, A. J. W. (1985), "Regular graphs of high degree are 1-factorizable", Proceedings of the London Mathematical Society, 50 (2): 193–206, doi:10.1112/plms/s3-50.2.193.
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Springer, ISBN 3-540-26182-6, Chapter 2: "Matching, covering and packing". Electronic edition.
- Harary, Frank (1969), Graph Theory, Addison-Wesley, ISBN 0-201-02787-9, Chapter 9: "Factorization".
- "One-factorization", Encyclopedia of Mathematics, EMS Press, 2001
- Niessen, Thomas (1994), "How to find overfull subgraphs in graphs with large maximum degree", Discrete Applied Mathematics, 51 (1–2): 117–125, doi:10.1016/0166-218X(94)90101-5.
- Perkovic, L.; Reed, B. (1997), "Edge coloring regular graphs of high degree", Discrete Mathematics, 165–166: 567–578, doi:10.1016/S0012-365X(96)00202-6.
- Petersen, Julius (1891), "Die Theorie der regulären graphs" (PDF), Acta Mathematica, 15: 193–220, doi:10.1007/BF02392606.
- West, Douglas B. "1-Factorization Conjecture (1985?)". Open Problems – Graph Theory and Combinatorics. Retrieved 2010-01-09.
- Weisstein, Eric W. "Graph Factor". MathWorld.
- Weisstein, Eric W. "k-Factor". MathWorld.
- Weisstein, Eric W. "k-Factorable Graph". MathWorld.
Further reading
- Plummer, Michael D. (2007), "Graph factors and factorization: 1985–2003: A survey", Discrete Mathematics, 307 (7–8): 791–821, doi:10.1016/j.disc.2005.11.059.