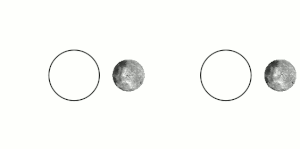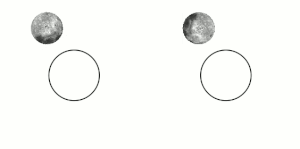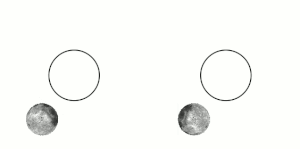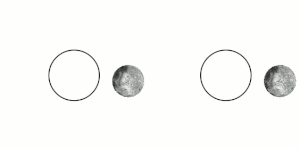
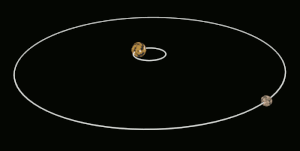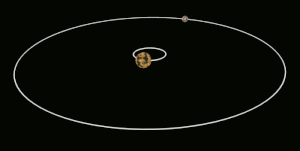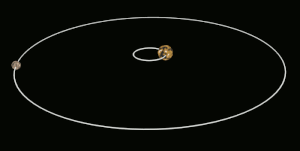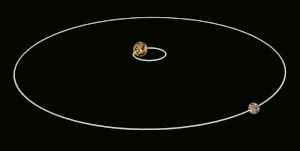
Tidal locking between a pair of co-orbiting astronomical bodies occurs when one of the objects reaches a state where there is no longer any net change in its rotation rate over the course of a complete orbit. In the case where a tidally locked body possesses synchronous rotation, the object takes just as long to rotate around its own axis as it does to revolve around its partner. For example, the same side of the Moon always faces Earth, although there is some variability because the Moon's orbit is not perfectly circular. Usually, only the satellite is tidally locked to the larger body. However, if both the difference in mass between the two bodies and the distance between them are relatively small, each may be tidally locked to the other; this is the case for Pluto and Charon, and for Eris and Dysnomia. Alternative names for the tidal locking process are gravitational locking, captured rotation, and spin–orbit locking.
The effect arises between two bodies when their gravitational interaction slows a body's rotation until it becomes tidally locked. Over many millions of years, the interaction forces changes to their orbits and rotation rates as a result of energy exchange and heat dissipation. When one of the bodies reaches a state where there is no longer any net change in its rotation rate over the course of a complete orbit, it is said to be tidally locked. The object tends to stay in this state because leaving it would require adding energy back into the system. The object's orbit may migrate over time so as to undo the tidal lock, for example, if a giant planet perturbs the object.
There is ambiguity in the use of the terms 'tidally locked' and 'tidal locking', in that some scientific sources use it to refer exclusively to 1:1 synchronous rotation (e.g. the Moon), while others include non-synchronous orbital resonances in which there is no further transfer of angular momentum over the course of one orbit (e.g. Mercury). In Mercury's case, the planet completes three rotations for every two revolutions around the Sun, a 3:2 spin–orbit resonance. In the special case where an orbit is nearly circular and the body's rotation axis is not significantly tilted, such as the Moon, tidal locking results in the same hemisphere of the revolving object constantly facing its partner. Regardless of which definition of tidal locking is used, the hemisphere that is visible changes slightly due to variations in the locked body's orbital velocity and the inclination of its rotation axis over time.
Mechanism
Further information: Centers of gravity in non-uniform fields
Consider a pair of co-orbiting objects, A and B. The change in rotation rate necessary to tidally lock body B to the larger body A is caused by the torque applied by A's gravity on bulges it has induced on B by tidal forces.
The gravitational force from object A upon B will vary with distance, being greatest at the nearest surface to A and least at the most distant. This creates a gravitational gradient across object B that will distort its equilibrium shape slightly. The body of object B will become elongated along the axis oriented toward A, and conversely, slightly reduced in dimension in directions orthogonal to this axis. The elongated distortions are known as tidal bulges. (For the solid Earth, these bulges can reach displacements of up to around 0.4 m or 1 ft 4 in.) When B is not yet tidally locked, the bulges travel over its surface due to orbital motions, with one of the two "high" tidal bulges traveling close to the point where body A is overhead. For large astronomical bodies that are nearly spherical due to self-gravitation, the tidal distortion produces a slightly prolate spheroid, i.e. an axially symmetric ellipsoid that is elongated along its major axis. Smaller bodies also experience distortion, but this distortion is less regular.
The material of B exerts resistance to this periodic reshaping caused by the tidal force. In effect, some time is required to reshape B to the gravitational equilibrium shape, by which time the forming bulges have already been carried some distance away from the A–B axis by B's rotation. Seen from a vantage point in space, the points of maximum bulge extension are displaced from the axis oriented toward A. If B's rotation period is shorter than its orbital period, the bulges are carried forward of the axis oriented toward A in the direction of rotation, whereas if B's rotation period is longer, the bulges instead lag behind.
Because the bulges are now displaced from the A–B axis, A's gravitational pull on the mass in them exerts a torque on B. The torque on the A-facing bulge acts to bring B's rotation in line with its orbital period, whereas the "back" bulge, which faces away from A, acts in the opposite sense. However, the bulge on the A-facing side is closer to A than the back bulge by a distance of approximately B's diameter, and so experiences a slightly stronger gravitational force and torque. The net resulting torque from both bulges, then, is always in the direction that acts to synchronize B's rotation with its orbital period, leading eventually to tidal locking.
Orbital changes
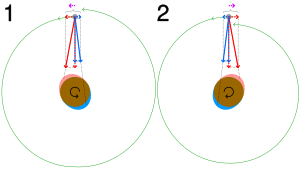
In (2) with the rotation reversed, the net force opposes the satellite's direction of orbit, lowering it (tidal deceleration).

The angular momentum of the whole A–B system is conserved in this process, so that when B slows down and loses rotational angular momentum, its orbital angular momentum is boosted by a similar amount (there are also some smaller effects on A's rotation). This results in a raising of B's orbit about A in tandem with its rotational slowdown. For the other case where B starts off rotating too slowly, tidal locking both speeds up its rotation, and lowers its orbit.
Locking of the larger body
See also: Synchronous orbitThe tidal locking effect is also experienced by the larger body A, but at a slower rate because B's gravitational effect is weaker due to B's smaller mass. For example, Earth's rotation is gradually being slowed by the Moon, by an amount that becomes noticeable over geological time as revealed in the fossil record. Current estimations are that this (together with the tidal influence of the Sun) has helped lengthen the Earth day from about 6 hours to the current 24 hours (over about 4.5 billion years). Currently, atomic clocks show that Earth's day lengthens, on average, by about 2.3 milliseconds per century. Given enough time, this would create a mutual tidal locking between Earth and the Moon. The length of Earth's day would increase and the length of a lunar month would also increase. Earth's sidereal day would eventually have the same length as the Moon's orbital period, about 47 times the length of the Earth day at present. However, Earth is not expected to become tidally locked to the Moon before the Sun becomes a red giant and engulfs Earth and the Moon.
For bodies of similar size the effect may be of comparable size for both, and both may become tidally locked to each other on a much shorter timescale. An example is the dwarf planet Pluto and its satellite Charon. They have already reached a state where Charon is visible from only one hemisphere of Pluto and vice versa.
Eccentric orbits
A widely spread misapprehension is that a tidally locked body permanently turns one side to its host.
— Heller et al. (2011)
For orbits that do not have an eccentricity close to zero, the rotation rate tends to become locked with the orbital speed when the body is at periapsis, which is the point of strongest tidal interaction between the two objects. If the orbiting object has a companion, this third body can cause the rotation rate of the parent object to vary in an oscillatory manner. This interaction can also drive an increase in orbital eccentricity of the orbiting object around the primary – an effect known as eccentricity pumping.
In some cases where the orbit is eccentric and the tidal effect is relatively weak, the smaller body may end up in a so-called spin–orbit resonance, rather than being tidally locked. Here, the ratio of the rotation period of a body to its own orbital period is some simple fraction different from 1:1. A well known case is the rotation of Mercury, which is locked to its own orbit around the Sun in a 3:2 resonance. This results in the rotation speed roughly matching the orbital speed around perihelion.
Many exoplanets (especially the close-in ones) are expected to be in spin–orbit resonances higher than 1:1. A Mercury-like terrestrial planet can, for example, become captured in a 3:2, 2:1, or 5:2 spin–orbit resonance, with the probability of each being dependent on the orbital eccentricity.
Occurrence
Moons

All twenty known moons in the Solar System that are large enough to be round are tidally locked with their primaries, because they orbit very closely and tidal force increases rapidly (as a cubic function) with decreasing distance. On the other hand, most of the irregular outer satellites of the giant planets (e.g. Phoebe), which orbit much farther away than the large well-known moons, are not tidally locked.
Pluto and Charon are an extreme example of a tidal lock. Charon is a relatively large moon in comparison to its primary and also has a very close orbit. This results in Pluto and Charon being mutually tidally locked. Pluto's other moons are not tidally locked; Styx, Nix, Kerberos, and Hydra all rotate chaotically due to the influence of Charon. Similarly, Eris and Dysnomia are mutually tidally locked. Orcus and Vanth might also be mutually tidally locked, but the data is not conclusive.
The tidal locking situation for asteroid moons is largely unknown, but closely orbiting binaries are expected to be tidally locked, as well as contact binaries.
Earth's Moon

Earth's Moon's rotation and orbital periods are tidally locked with each other, so no matter when the Moon is observed from Earth, the same hemisphere of the Moon is always seen. Most of the far side of the Moon was not seen until 1959, when photographs of most of the far side were transmitted from the Soviet spacecraft Luna 3.
When Earth is observed from the Moon, Earth does not appear to move across the sky. It remains in the same place while showing nearly all its surface as it rotates on its axis.
Despite the Moon's rotational and orbital periods being exactly locked, about 59 percent of the Moon's total surface may be seen with repeated observations from Earth, due to the phenomena of libration and parallax. Librations are primarily caused by the Moon's varying orbital speed due to the eccentricity of its orbit: this allows up to about 6° more along its perimeter to be seen from Earth. Parallax is a geometric effect: at the surface of Earth observers are offset from the line through the centers of Earth and Moon; this accounts for about a 1° difference in the Moon's surface which can be seen around the sides of the Moon when comparing observations made during moonrise and moonset.
Planets
It was thought for some time that Mercury was in synchronous rotation with the Sun. This was because whenever Mercury was best placed for observation, the same side faced inward. Radar observations in 1965 demonstrated instead that Mercury has a 3:2 spin–orbit resonance, rotating three times for every two revolutions around the Sun, which results in the same positioning at those observation points. Modeling has demonstrated that Mercury was captured into the 3:2 spin–orbit state very early in its history, probably within 10–20 million years after its formation.
The 583.92-day interval between successive close approaches of Venus to Earth is equal to 5.001444 Venusian solar days, making approximately the same face visible from Earth at each close approach. Whether this relationship arose by chance or is the result of some kind of tidal locking with Earth is unknown.
The exoplanet Proxima Centauri b discovered in 2016 which orbits around Proxima Centauri, is almost certainly tidally locked, expressing either synchronized rotation or a 3:2 spin–orbit resonance like that of Mercury.
One form of hypothetical tidally locked exoplanets are eyeball planets, which in turn are divided into "hot" and "cold" eyeball planets.
Stars
Close binary stars throughout the universe are expected to be tidally locked with each other, and extrasolar planets that have been found to orbit their primaries extremely closely are also thought to be tidally locked to them. An unusual example, confirmed by MOST, may be Tau Boötis, a star that is probably tidally locked by its planet Tau Boötis b. If so, the tidal locking is almost certainly mutual.
Timescale
An estimate of the time for a body to become tidally locked can be obtained using the following formula:
where
- is the initial spin rate expressed in radians per second,
- is the semi-major axis of the motion of the satellite around the planet (given by the average of the periapsis and apoapsis distances),
- is the moment of inertia of the satellite, where is the mass of the satellite and is the mean radius of the satellite,
- is the dissipation function of the satellite,
- is the gravitational constant,
- is the mass of the planet (i.e., the object being orbited), and
- is the tidal Love number of the satellite.
and are generally very poorly known except for the Moon, which has . For a really rough estimate it is common to take (perhaps conservatively, giving overestimated locking times), and
where
- is the density of the satellite
- is the surface gravity of the satellite
- is the rigidity of the satellite. This can be roughly taken as 3×10 N/m for rocky objects and 4×10 N/m for icy ones.
Even knowing the size and density of the satellite leaves many parameters that must be estimated (especially ω, Q, and μ), so that any calculated locking times obtained are expected to be inaccurate, even to factors of ten. Further, during the tidal locking phase the semi-major axis may have been significantly different from that observed nowadays due to subsequent tidal acceleration, and the locking time is extremely sensitive to this value.
Because the uncertainty is so high, the above formulas can be simplified to give a somewhat less cumbersome one. By assuming that the satellite is spherical, , and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)
with masses in kilograms, distances in meters, and in newtons per meter squared; can be roughly taken as 3×10 N/m for rocky objects and 4×10 N/m for icy ones.
There is an extremely strong dependence on semi-major axis .
For the locking of a primary body to its satellite as in the case of Pluto, the satellite and primary body parameters can be swapped.
One conclusion is that, other things being equal (such as and ), a large moon will lock faster than a smaller moon at the same orbital distance from the planet because grows as the cube of the satellite radius . A possible example of this is in the Saturn system, where Hyperion is not tidally locked, whereas the larger Iapetus, which orbits at a greater distance, is. However, this is not clear cut because Hyperion also experiences strong driving from the nearby Titan, which forces its rotation to be chaotic.
The above formulae for the timescale of locking may be off by orders of magnitude, because they ignore the frequency dependence of . More importantly, they may be inapplicable to viscous binaries (double stars, or double asteroids that are rubble), because the spin–orbit dynamics of such bodies is defined mainly by their viscosity, not rigidity.
List of known tidally locked bodies
Solar System
All the bodies below are tidally locked, and all but Mercury are moreover in synchronous rotation. (Mercury is tidally locked, but not in synchronous rotation.)
| Parent body | Tidally-locked satellites |
|---|---|
| Sun | Mercury (3:2 spin–orbit resonance) |
| Earth | Moon |
| Mars | Phobos · Deimos |
| Jupiter | Metis · Adrastea · Amalthea · Thebe · Io · Europa · Ganymede · Callisto |
| Saturn | Pan · Atlas · Prometheus · Pandora · Epimetheus · Janus · Mimas · Enceladus · Telesto · Tethys · Calypso · Dione · Rhea · Titan · Iapetus |
| Uranus | Miranda · Ariel · Umbriel · Titania · Oberon |
| Neptune | Proteus · Triton |
| Pluto | Charon (mutually locked) |
| Eris | Dysnomia (mutually locked) |
Extra-solar
- The most successful detection methods of exoplanets (transits and radial velocities) suffer from a clear observational bias favoring the detection of planets near the star; thus, 85% of the exoplanets detected are inside the tidal locking zone, which makes it difficult to estimate the true incidence of this phenomenon. Tau Boötis is known to be locked to the close-orbiting giant planet Tau Boötis b.
Bodies likely to be locked
Solar System
Based on comparison between the likely time needed to lock a body to its primary, and the time it has been in its present orbit (comparable with the age of the Solar System for most planetary moons), a number of moons are thought to be locked. However their rotations are not known or not known enough. These are:
Probably locked to Saturn
Probably locked to Uranus
Probably locked to Neptune
Probably mutually tidally locked
Extrasolar
- Gliese 581c, Gliese 581g, Gliese 581b, and Gliese 581e may be tidally locked to their parent star Gliese 581. Gliese 581d is almost certainly captured either into the 2:1 or the 3:2 spin–orbit resonance with the same star.
- All planets in the TRAPPIST-1 system are likely to be tidally locked.
See also
- Conservation of angular momentum – Conserved physical quantity; rotational analogue of linear momentumPages displaying short descriptions of redirect targets
- Gravity-gradient stabilization – Method for the stabilization and the orientation of various spacecraft
- Kozai mechanism – Dynamical phenomenon affecting the orbit of a binary system perturbed by a distant third body
- Orbital resonance – Regular and periodic mutual gravitational influence of orbiting bodies
- Planetary habitability – Known extent to which a planet is suitable for life
- Pseudo-synchronous rotation – a near synchronization of revolution and rotation at periastron
- Roche limit – Orbital radius at which a satellite might break up due to gravitational force
- Synchronous orbit – Orbit of an astronomical body equal to that body's average rotational period
- Tidal acceleration – Natural phenomenon due to which tidal locking occurs
- Rotation around a fixed axis – Type of motion
References
- "When Will Earth Lock to the Moon?". Universe Today. 2016-04-12. Archived from the original on 2016-09-23. Retrieved 2017-01-02.
- ^ Clouse, Christopher; et al. (May 2022), "Spin-orbit gravitational locking-an effective potential approach", European Journal of Physics, 43 (3): 13, arXiv:2203.09297, Bibcode:2022EJPh...43c5602C, doi:10.1088/1361-6404/ac5638, S2CID 246962304, 035602
- ^ Barnes, Rory, ed. (2010). Formation and Evolution of Exoplanets. John Wiley & Sons. p. 248. ISBN 978-3527408962. Archived from the original on 2023-08-06. Retrieved 2016-08-16.
- ^ Heller, R.; Leconte, J.; Barnes, R. (April 2011). "Tidal obliquity evolution of potentially habitable planets". Astronomy & Astrophysics. 528: 16. arXiv:1101.2156. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809. S2CID 118784209. A27.
- Mahoney, T. J. (2013). Mercury. Springer Science & Business Media. ISBN 978-1461479512. Archived from the original on 2023-08-06. Retrieved 2018-04-20.
- Lewis, John (2012). Physics and Chemistry of the Solar System. Academic Press. pp. 242–243. ISBN 978-0323145848. Archived from the original on 2023-08-06. Retrieved 2018-02-22.
- Watson, C.; et al. (April 2006). "Impact of solid Earth tide models on GPS coordinate and tropospheric time series" (PDF). Geophysical Research Letters. 33 (8): L08306. Bibcode:2006GeoRL..33.8306W. doi:10.1029/2005GL025538. hdl:1885/21511. Archived (PDF) from the original on 2021-11-26. Retrieved 2018-05-18.
- de Pater, Imke (2001). Planetary Sciences. Cambridge. p. 34. ISBN 978-0521482196.
- Ray, R. (15 May 2001). "Ocean Tides and the Earth's Rotation". IERS Special Bureau for Tides. Archived from the original on 18 August 2000. Retrieved 17 March 2010.
- Murray, C. D.; Dermott, Stanley F. (1999). Solar System Dynamics. Cambridge University Press. p. 184. ISBN 978-0-521-57295-8.
- Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. pp. 79–81. ISBN 978-0-921820-71-0.
- ^ Michaely, Erez; et al. (February 2017), "On the Existence of Regular and Irregular Outer Moons Orbiting the Pluto–Charon System", The Astrophysical Journal, 836 (1): 7, arXiv:1506.08818, Bibcode:2017ApJ...836...27M, doi:10.3847/1538-4357/aa52b2, S2CID 118068933, 27
- Correia, Alexandre C. M.; Boué, Gwenaël; Laskar, Jacques (January 2012), "Pumping the Eccentricity of Exoplanets by Tidal Effect", The Astrophysical Journal Letters, 744 (2): 5, arXiv:1111.5486, Bibcode:2012ApJ...744L..23C, doi:10.1088/2041-8205/744/2/L23, S2CID 118695308, L23.
- Colombo, G. (November 1965), "Rotational Period of the Planet Mercury", Nature, 208 (5010): 575, Bibcode:1965Natur.208..575C, doi:10.1038/208575a0, S2CID 4213296
- Makarov, Valeri V. (June 2012), "Conditions of Passage and Entrapment of Terrestrial Planets in Spin–orbit Resonances", The Astrophysical Journal, 752 (1): 8, arXiv:1110.2658, Bibcode:2012ApJ...752...73M, doi:10.1088/0004-637X/752/1/73, S2CID 119227632, 73
- Schutz, Bernard (2003-12-04). Gravity from the Ground Up. Cambridge University Press. p. 43. ISBN 9780521455060. Archived from the original on 2023-08-06. Retrieved 24 April 2017.
- Showalter, M. R.; Hamilton, D. P. (June 2015). "Resonant interactions and chaotic rotation of Pluto's small moons" (PDF). Nature. 522 (7554): 45–49. Bibcode:2015Natur.522...45S. doi:10.1038/nature14469. PMID 26040889. S2CID 205243819. Archived (PDF) from the original on 2022-06-08. Retrieved 2022-03-25.
- ^ Szakáts, R.; Kiss, Cs.; Ortiz, J. L.; Morales, N.; Pál, A.; Müller, T. G.; et al. (2023). "Tidally locked rotation of the dwarf planet (136199) Eris discovered from long-term ground based and space photometry". Astronomy & Astrophysics. L3: 669. arXiv:2211.07987. Bibcode:2023A&A...669L...3S. doi:10.1051/0004-6361/202245234. S2CID 253522934.
- Ortiz, J. L.; Cikota, A.; Cikota, S.; Hestroffer, D.; Thirouin, A.; Morales, N.; Duffard, R.; Gil-Hutton, R.; Santos-Sanz, P.; De La Cueva, I. (2010). "A mid-term astrometric and photometric study of trans-Neptunian object (90482) Orcus". Astronomy & Astrophysics. 525: A31. arXiv:1010.6187. Bibcode:2011A&A...525A..31O. doi:10.1051/0004-6361/201015309. S2CID 56051949.
- "Oct. 7, 1959 – Our First Look at the Far Side of the Moon". Universe Today. 2013-10-07. Archived from the original on 2022-08-12. Retrieved 2015-02-15.
- Cain, Fraser (2016-04-11). "When Will Earth Lock to the Moon?". Universe Today. Archived from the original on 2022-05-28. Retrieved 2020-08-03.
- Grego, Peter (2006). The Moon and How to Observe It. Springer London. pp. 47–50. ISBN 9781846282430. Archived from the original on 2023-10-21. Retrieved 2023-03-19.
- ^ Noyelles, Benoit; Frouard, Julien; Makarov, Valeri V. & Efroimsky, Michael (2014). "Spin–orbit evolution of Mercury revisited". Icarus. 241: 26–44. arXiv:1307.0136. Bibcode:2014Icar..241...26N. doi:10.1016/j.icarus.2014.05.045. S2CID 53690707.
- Gold, T.; Soter, S. (1969). "Atmospheric tides and the resonant rotation of Venus". Icarus. 11 (3): 356–366. Bibcode:1969Icar...11..356G. doi:10.1016/0019-1035(69)90068-2.
- Barnes, Rory (2017). "Tidal locking of habitable exoplanets". Celestial Mechanics and Dynamical Astronomy. 129 (4). Springer: 509–536. arXiv:1708.02981. Bibcode:2017CeMDA.129..509B. doi:10.1007/s10569-017-9783-7. S2CID 119384474. Archived from the original on 2021-02-26. Retrieved 2021-03-29.
- Sean Raymond (20 February 2015). "Forget "Earth-Like"—We'll First Find Aliens on Eyeball Planets". Nautilus. Archived from the original on 23 June 2017. Retrieved 5 June 2017.
- Starr, Michelle (5 January 2020). "Eyeball Planets Might Exist, And They're as Creepy as They Sound". ScienceAlert.com. Archived from the original on 6 January 2020. Retrieved 6 January 2020.
- ^ Schirber, Michael (2005-05-23). "Role Reversal: Planet Controls a Star". space.com. Archived from the original on 2008-08-04. Retrieved 2018-04-21.
- Singal, Ashok K. (May 2014). "Life on a tidally-locked planet". Planex Newsletter. 4 (2): 8. arXiv:1405.1025. Bibcode:2014arXiv1405.1025S.
- Walker, G. A. H.; et al. (2008). "MOST detects variability on tau Bootis possibly induced by its planetary companion". Astronomy and Astrophysics. 482 (2): 691–697. arXiv:0802.2732. Bibcode:2008A&A...482..691W. doi:10.1051/0004-6361:20078952. S2CID 56317105. Archived from the original on 2021-02-25. Retrieved 2019-05-16.
- B. Gladman; et al. (1996). "Synchronous Locking of Tidally Evolving Satellites". Icarus. 122 (1): 166–192. Bibcode:1996Icar..122..166G. doi:10.1006/icar.1996.0117. (See pages 169–170 of this article. Formula (9) is quoted here, which comes from S. J. Peale, Rotation histories of the natural satellites, in J. A. Burns, ed. (1977). Planetary Satellites. Tucson: University of Arizona Press. pp. 87–112.)
- Hanslmeier, Arnold (2018). Planetary Habitability And Stellar Activity. World Scientific Publishing Company. p. 99. ISBN 9789813237445. Archived from the original on 2023-10-04. Retrieved 2023-03-19.
- Efroimsky, M. (2015). "Tidal Evolution of Asteroidal Binaries. Ruled by Viscosity. Ignorant of Rigidity". The Astronomical Journal. 150 (4): 12. arXiv:1506.09157. Bibcode:2015AJ....150...98E. doi:10.1088/0004-6256/150/4/98. S2CID 119283628. 98.
- Nobili, A. M. (April 1978), "Secular effects of tidal friction on the planet–satellite systems of the solar system", Moon and the Planets, 18 (2): 203–216, Bibcode:1978M&P....18..203N, doi:10.1007/BF00896743, S2CID 121510792. "The following satellites seem to corotate: Phobos and Deimos, Amalthea, Io, Europa, Ganymede, Callisto, Janus, Mimas, Enceladus, Tethys, Dione, Rhea, Titan, Hyperion, Japetus, Miranda, Ariel, Umbriel, Titania, and Oberon."
- Peale, S. J. (1988), "The rotational dynamics of Mercury and the state of its core", Mercury, University of Arizona Press: 461–493, Bibcode:1988merc.book..461P.
- Rivoldini, A.; et al. (September 2010), "Past and present tidal dissipation in Mercury", European Planetary Science Congress 2010: 671, Bibcode:2010epsc.conf..671R.
- "The Moon's Orbit and Rotation". Moon: NASA Science. Archived from the original on 2023-08-01. Retrieved 2023-08-24.
- ^ Correia, Alexandre C. M. (October 2009), "Secular Evolution of a Satellite by Tidal Effect: Application to Triton", The Astrophysical Journal Letters, 704 (1): L1 – L4, arXiv:0909.4210, Bibcode:2009ApJ...704L...1C, doi:10.1088/0004-637X/704/1/L1, S2CID 15378780.
- Burns, J. A. (1978), "The dynamical evolution and origin of the Martian moons", Vistas in Astronomy, 22 (2): 193–208, Bibcode:1978VA.....22..193B, doi:10.1016/0083-6656(78)90015-6.
- ^ Burns, Joseph A.; et al. (2004), Bagenal, Fran; Dowling, Timothy E.; McKinnon, William B. (eds.), "Jupiter's Ring-Moon System" (PDF), Jupiter: The Planet, Satellites and Magnetosphere, Cambridge University Press, pp. 241–262, Bibcode:2004jpsm.book..241B, ISBN 978-0-521-81808-7, archived (PDF) from the original on 2006-05-12, retrieved 2021-05-07
- ^ Dougherty, Michele K.; Spilker, Linda J. (June 2018), "Review of Saturn's icy moons following the Cassini mission", Reports on Progress in Physics, 81 (6): 065901, Bibcode:2018RPPh...81f5901D, doi:10.1088/1361-6633/aabdfb, hdl:10044/1/63567, PMID 29651989, S2CID 4810803, 065901
- Cartwright, Richard J.; et al. (November 2018), "Red material on the large moons of Uranus: Dust from the irregular satellites?", Icarus, 314: 210–231, arXiv:1806.01809, Bibcode:2018Icar..314..210C, doi:10.1016/j.icarus.2018.06.004, S2CID 119243937
- Stooke, Philip J. (January 1994), "The Surfaces of Larissa and Proteus", Earth, Moon, and Planets, 65 (1): 3–54, Bibcode:1994EM&P...65...31S, doi:10.1007/BF00572198
- F. J. Ballesteros; A. Fernandez-Soto; V. J. Martinez (2019). "Title: Diving into Exoplanets: Are Water Seas the Most Common?". Astrobiology. 19 (5): 642–654. doi:10.1089/ast.2017.1720. hdl:10261/213115. PMID 30789285. S2CID 73498809.
- Brown, Michael E.; Butler, Bryan (July 2023). "Masses and densities of dwarf planet satellites measured with ALMA". The Planetary Science Journal. 4 (10): 11. arXiv:2307.04848. Bibcode:2023PSJ.....4..193B. doi:10.3847/PSJ/ace52a.
- Vergano, Dan (2007-04-25). "Out of our world: Earthlike planet". USA Today. Archived from the original on 2011-05-23. Retrieved 2010-05-25.
- "Astronomers Find Most Earth-like Planet to Date". Science, USA. September 29, 2010. Archived from the original on October 2, 2010. Retrieved September 30, 2010.
- "Gliese 581g the most Earth like planet yet discovered". The Daily Telegraph, UK. September 30, 2010. Archived from the original on October 2, 2010. Retrieved September 30, 2010.
- "Gliese 581". Open Exoplanet Catalogue. Archived from the original on 7 April 2022. Retrieved 16 May 2019.
- "Gliese 581". Encyclopedia Britannica. Archived from the original on 6 August 2023. Retrieved 16 May 2019.
- Makarov, V. V.; Berghea, C. & Efroimsky, M. (2012). "Dynamical Evolution and Spin–Orbit Resonances of Potentially Habitable Exoplanets: The Case of GJ 581d". The Astrophysical Journal. 761 (2): 83. arXiv:1208.0814. Bibcode:2012ApJ...761...83M. doi:10.1088/0004-637X/761/2/83. S2CID 926755. 83.
- "NASA Telescope Reveals Largest Batch of Earth-Size, Habitable-Zone Planets Around Single Star" (Press release). NASA. 22 February 2017. Archived from the original on 5 March 2017. Retrieved 23 February 2017.
- Gillon, Michaël; Triaud, Amaury H. M. J.; Demory, Brice-Olivier; Jehin, Emmanuël; Agol, Eric; Deck, Katherine M.; Lederer, Susan M.; de Wit, Julien; Burdanov, Artem (2017-02-23). "Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1". Nature. 542 (7642): 456–460. arXiv:1703.01424. Bibcode:2017Natur.542..456G. doi:10.1038/nature21360. ISSN 0028-0836. PMC 5330437. PMID 28230125.
| Moon | ||
|---|---|---|
| Outline | ||
| Physical properties |  | |
| Orbit | ||
| Surface and features | ||
| Science | ||
| Exploration | ||
| Time-telling and navigation | ||
| Phases and names | ||
| Daily phenomena | ||
| Related |
| |

 is the initial spin rate expressed in
is the initial spin rate expressed in  is the
is the 
 is the
is the  is the mass of the satellite and
is the mass of the satellite and  is the
is the  is the
is the  is the
is the  is the mass of the planet (i.e., the object being orbited), and
is the mass of the planet (i.e., the object being orbited), and is the tidal
is the tidal  and
and  are generally very poorly known except for the Moon, which has
are generally very poorly known except for the Moon, which has  . For a really rough estimate it is common to take
. For a really rough estimate it is common to take  (perhaps conservatively, giving overestimated locking times), and
(perhaps conservatively, giving overestimated locking times), and

 is the density of the satellite
is the density of the satellite is the surface gravity of the satellite
is the surface gravity of the satellite is the rigidity of the satellite. This can be roughly taken as 3×10 N/m for rocky objects and 4×10 N/m for icy ones.
is the rigidity of the satellite. This can be roughly taken as 3×10 N/m for rocky objects and 4×10 N/m for icy ones. may have been significantly different from that observed nowadays due to subsequent
may have been significantly different from that observed nowadays due to subsequent  , and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)
, and it is sensible to guess one revolution every 12 hours in the initial non-locked state (most asteroids have rotational periods between about 2 hours and about 2 days)

 in newtons per meter squared;
in newtons per meter squared;  grows as the cube of the satellite radius
grows as the cube of the satellite radius  . More importantly, they may be inapplicable to viscous binaries (double stars, or double asteroids that are rubble), because the spin–orbit dynamics of such bodies is defined mainly by their viscosity, not rigidity.
. More importantly, they may be inapplicable to viscous binaries (double stars, or double asteroids that are rubble), because the spin–orbit dynamics of such bodies is defined mainly by their viscosity, not rigidity.