| This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Hemipolyhedron" – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this message) |
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron – hence the "hemi" prefix.
The prefix "hemi" is also used to refer to certain projective polyhedra, such as the hemi-cube, which are the image of a 2 to 1 map of a spherical polyhedron with central symmetry.
Wythoff symbol and vertex figure
Their Wythoff symbols are of the form /(p − q) /q | r; their vertex figures are crossed quadrilaterals. They are thus related to the cantellated polyhedra, which have similar Wythoff symbols. The vertex configuration is /q.2r./(p − q).2r. The 2r-gon faces pass through the center of the model: if represented as faces of spherical polyhedra, they cover an entire hemisphere and their edges and vertices lie along a great circle. The /(p − q) notation implies a {/q} face turning backwards around the vertex figure.
The nine forms, listed with their Wythoff symbols and vertex configurations are:
 Tetrahemihexahedron /2 3 | 2 (3.4./2.4) (/q = 3, r = 2) |
 Octahemioctahedron /2 3 | 3 (3.6./2.6) (/q = 3, r = 3) |
 Small icosihemidodecahedron /2 3 | 5 (3.10./2.10) (/q = 3, r = 5) |
 Great icosihemidodecahedron /2 3 | /3 (3./3./2./3) (/q = 3, r = /3) |
 Small dodecahemicosahedron /3 /2 | 3 (/2.6./3.6) (/q = /2, r = 3) |
 Cubohemioctahedron /3 4 | 3 (4.6./3.6) (/q = 4, r = 3) |
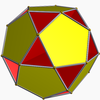 Small dodecahemidodecahedron /4 5 | 5 (5.10./4.10) (/q = 5, r = 5) |
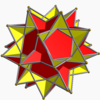 Great dodecahemidodecahedron /3 /2 | /3 (/2./3./3./3) (/q = /2, r = /3) |
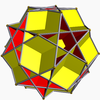 Great dodecahemicosahedron /4 5 | 3 (5.6./4.6) (/q = 5, r = 3) |
Note that Wythoff's kaleidoscopic construction generates the nonorientable hemipolyhedra (all except the octahemioctahedron) as double covers (two coincident hemipolyhedra).
In the Euclidean plane, the sequence of hemipolyhedra continues with the following four star tilings, where apeirogons appear as the aforementioned equatorial polygons:
Of these four tilings, only 6/5 6 | ∞ is generated as a double cover by Wythoff's construction.
Orientability
Only the octahemioctahedron represents an orientable surface; the remaining hemipolyhedra have non-orientable or single-sided surfaces. This is because proceeding around an equatorial 2r-gon, the /q-gonal faces alternately point "up" and "down", so any two consecutive ones have opposite senses. This is equivalent to demanding that the /q-gons in the corresponding quasiregular polyhedra below can be alternatively given positive and negative orientations. But that is only possible for the triangles of the cuboctahedron (corresponding to the triangles of the octahedron, the only regular polyhedron with an even number of faces meeting at a vertex), which are precisely the non-hemi faces of the octahemioctahedron.
Duals of the hemipolyhedra
Since the hemipolyhedra have faces passing through the center, the dual figures have corresponding vertices at infinity; properly, on the real projective plane at infinity. In Magnus Wenninger's Dual Models, they are represented with intersecting prisms, each extending in both directions to the same vertex at infinity, in order to maintain symmetry. In practice the model prisms are cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation figures, called stellation to infinity. However, he also suggested that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
There are 9 such duals, sharing only 5 distinct outward forms, four of them existing in outwardly identical pairs. The members of a given visually identical pair differ in their arrangements of true and false vertices (a false vertex is where two edges cross each other but do not join). The outward forms are:

|

|

|

|

|
| Tetrahemihexacron | Octahemioctacron and hexahemioctacron |
Small icosihemidodecacron and small dodecahemidodecacron |
Great dodecahemidodecacron and great icosihemidodecacron |
Great dodecahemicosacron and small dodecahemicosacron |
| 3 intersecting infinite square prisms | 4 intersecting infinite hexagonal prisms | 6 intersecting infinite decagonal prisms | 6 intersecting infinite decagrammic prisms | 10 intersecting infinite hexagonal prisms |
Relationship with the quasiregular polyhedra
The hemipolyhedra occur in pairs as facetings of the quasiregular polyhedra with four faces at a vertex. These quasiregular polyhedra have vertex configuration m.n.m.n and their edges, in addition to forming the m- and n-gonal faces, also form hemi-faces of the hemipolyhedra. Thus, the hemipolyhedra can be derived from the quasiregular polyhedra by discarding either the m-gons or n-gons (to maintain two faces at an edge) and then inserting the hemi faces. Since either m-gons or n-gons may be discarded, either of two hemipolyhedra may be derived from each quasiregular polyhedron, except for the octahedron as a tetratetrahedron, where m = n = 3 and the two facetings are congruent. (This construction does not work for the quasiregular polyhedra with six faces at a vertex, also known as the ditrigonal polyhedra, as their edges do not form any regular hemi-faces.)
Since the hemipolyhedra, like the quasiregular polyhedra, also have two types of faces alternating around each vertex, they are sometimes also considered to be quasiregular.
| Quasiregular polyhedron m.n.m.n |
Hemi-faces (h-gons) | Hemipolyhedron with m-gons discarded n.h./n - 1.h |
Hemipolyhedron with n-gons discarded m.h./m - 1.h |
|---|---|---|---|
 Tetratetrahedron 3.3.3.3 m = 3, n = 3 |
 squares {4} |
 Tetrahemihexahedron 3.4.3/2.4 |
 Tetrahemihexahedron 3.4.3/2.4 |
 Cuboctahedron 3.4.3.4 m = 3, n = 4 |
 hexagons {6} |
 Cubohemioctahedron 4.6.4/3.6 |
 Octahemioctahedron 3.6.3/2.6 |
 Icosidodecahedron 3.5.3.5 m = 3, n = 5 |
 decagons {10} |
 Small dodecahemidodecahedron 5.10.5/4.10 |
 Small icosihemidodecahedron 3.10.3/2.10 |
 Dodecadodecahedron 5.5/2.5.5/2 m = 5, n = 5/2 |
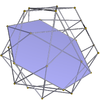 hexagons {6} |
 Small dodecahemicosahedron 5/2.6.5/3.6 |
 Great dodecahemicosahedron 5.6.5/4.6 |
 Great icosidodecahedron 3.5/2.3.5/2 m = 3, n = 5/2 |
 decagrams {10/3} |
 Great dodecahemidodecahedron 5/2.10/3.5/3.10/3 |
 Great icosihemidodecahedron 3.10/3.3/2.10/3 |
Here m and n correspond to /q above, and h corresponds to 2r above.
References
- ^ Hart, George (1996). "Quasiregular Polyhedra". Virtual Polyhedra: The Encyclopedia of Polyhedra. Retrieved 6 May 2012.
- Coxeter et al., p. 417
- (Wenninger 1983, p. 101)
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916), The Royal Society: 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446
- Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR 0467493 (Wenninger models: 67, 68, 78, 89, 91, 100, 102, 106, 107)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
- Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El (Page 10, 5.2. Hemi polyhedra p p'|r.)
External links
- Stella Polyhedral Glossary
- Versi-Regular Polyhedra in Visual Polyhedra









