For a general introduction, see State diagram.
| UML diagram types |
|---|
| Structural UML diagrams |
| Behavioral UML diagrams |
UML state machine, formerly known as UML statechart, is an extension of the mathematical concept of a finite automaton in computer science applications as expressed in the Unified Modeling Language (UML) notation.
The concepts behind it are about organizing the way a device, computer program, or other (often technical) process works such that an entity or each of its sub-entities is always in exactly one of a number of possible states and where there are well-defined conditional transitions between these states.
UML state machine is an object-based variant of Harel statechart, adapted and extended by UML. The goal of UML state machines is to overcome the main limitations of traditional finite-state machines while retaining their main benefits. UML statecharts introduce the new concepts of hierarchically nested states and orthogonal regions, while extending the notion of actions. UML state machines have the characteristics of both Mealy machines and Moore machines. They support actions that depend on both the state of the system and the triggering event, as in Mealy machines, as well as entry and exit actions, which are associated with states rather than transitions, as in Moore machines.
The term "UML state machine" can refer to two kinds of state machines: behavioral state machines and protocol state machines. Behavioral state machines can be used to model the behavior of individual entities (e.g., class instances), a subsystem, a package, or even an entire system. Protocol state machines are used to express usage protocols and can be used to specify the legal usage scenarios of classifiers, interfaces, and ports.
Basic state machine concepts
Many software systems are event-driven, which means that they continuously wait for the occurrence of some external or internal event such as a mouse click, a button press, a time tick, or an arrival of a data packet. After recognizing the event, such systems react by performing the appropriate computation that may include manipulating the hardware or generating “soft” events that trigger other internal software components. (That's why event-driven systems are alternatively called reactive systems.) Once the event handling is complete, the system goes back to waiting for the next event.
The response to an event generally depends on both the type of the event and on the internal state of the system and can include a change of state leading to a state transition. The pattern of events, states, and state transitions among those states can be abstracted and represented as a finite-state machine (FSM).
The concept of a FSM is important in event-driven programming because it makes the event handling explicitly dependent on both the event-type and on the state of the system. When used correctly, a state machine can drastically cut down the number of execution paths through the code, simplify the conditions tested at each branching point, and simplify the switching between different modes of execution. Conversely, using event-driven programming without an underlying FSM model can lead programmers to produce error prone, difficult to extend and excessively complex application code.
Basic UML state diagrams
UML preserves the general form of the traditional state diagrams. The UML state diagrams are directed graphs in which nodes denote states and connectors denote state transitions. For example, Figure 1 shows a UML state diagram corresponding to the computer keyboard state machine. In UML, states are represented as rounded rectangles labeled with state names. The transitions, represented as arrows, are labeled with the triggering events followed optionally by the list of executed actions. The initial transition originates from the solid circle and specifies the default state when the system first begins. Every state diagram should have such a transition, which should not be labeled, since it is not triggered by an event. The initial transition can have associated actions.
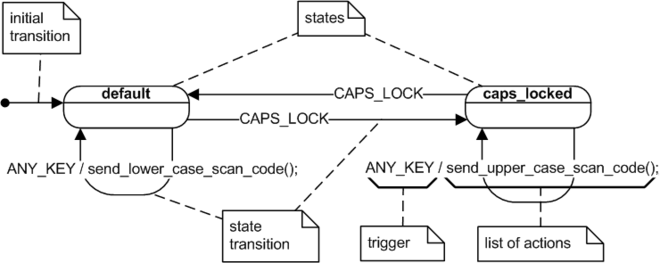
Events
An event is something that happens that affects the system. Strictly speaking, in the UML specification, the term event refers to the type of occurrence rather than to any concrete instance of that occurrence. For example, Keystroke is an event for the keyboard, but each press of a key is not an event but a concrete instance of the Keystroke event. Another event of interest for the keyboard might be Power-on, but turning the power on tomorrow at 10:05:36 will be just an instance of the Power-on event.
An event can have associated parameters, allowing the event instance to convey not only the occurrence of some interesting incident but also quantitative information regarding that occurrence. For example, the Keystroke event generated by pressing a key on a computer keyboard has associated parameters that convey the character scan code as well as the status of the Shift, Ctrl, and Alt keys.
An event instance outlives the instantaneous occurrence that generated it and might convey this occurrence to one or more state machines. Once generated, the event instance goes through a processing life cycle that can consist of up to three stages. First, the event instance is received when it is accepted and waiting for processing (e.g., it is placed on the event queue). Later, the event instance is dispatched to the state machine, at which point it becomes the current event. Finally, it is consumed when the state machine finishes processing the event instance. A consumed event instance is no longer available for processing.
States
Each state machine has a state, which governs reaction of the state machine to events. For example, when you strike a key on a keyboard, the character code generated will be either an uppercase or a lowercase character, depending on whether the Caps Lock is active. Therefore, the keyboard's behavior can be divided into two states: the "default" state and the "caps_locked" state. (Most keyboards include an LED that indicates that the keyboard is in the "caps_locked" state.) The behavior of a keyboard depends only on certain aspects of its history, namely whether the Caps Lock key has been pressed, but not, for example, on how many and exactly which other keys have been pressed previously. A state can abstract away all possible (but irrelevant) event sequences and capture only the relevant ones.
In the context of software state machines (and especially classical FSMs), the term state is often understood as a single state variable that can assume only a limited number of a priori determined values (e.g., two values in case of the keyboard, or more generally - some kind of variable with an enum type in many programming languages). The idea of state variable (and classical FSM model) is that the value of the state variable fully defines the current state of the system at any given time. The concept of the state reduces the problem of identifying the execution context in the code to testing just the state variable instead of many variables, thus eliminating a lot of conditional logic.
Extended states
In practice, however, interpreting the whole state of the state machine as a single state variable quickly becomes impractical for all state machines beyond very simple ones. Indeed, even if we have a single 32-bit integer in our machine state, it could contribute to over 4 billion different states - and will lead to a premature state explosion. This interpretation is not practical, so in UML state machines the whole state of the state machine is commonly split into (a) an enumerable state variable and (b) all the other variables which are named extended state. Another way to see it is to interpret the enumerable state variable as a qualitative aspect and the extended state as quantitative aspects of the whole state. In this interpretation, a change of variable does not always imply a change of the qualitative aspects of the system behavior and therefore does not lead to a change of state.
State machines supplemented with extended state variables are called extended state machines and UML state machines belong to this category. Extended state machines can apply the underlying formalism to much more complex problems than is practical without including extended state variables. For example, if we have to implement some kind of limit in our FSM (say, limiting number of keystrokes on keyboard to 1000), without extended state we'd need to create and process 1000 states - which is not practical; however, with an extended state machine we can introduce a key_count variable, which is initialized to 1000 and decremented by every keystroke without changing state variable.
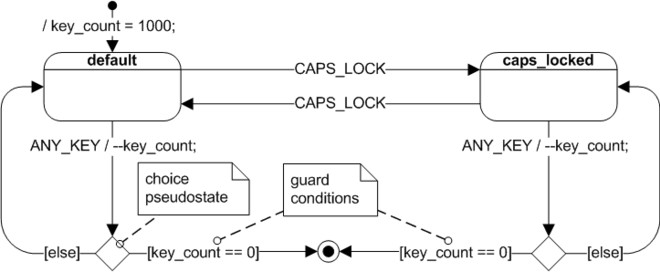
The state diagram from Figure 2 is an example of an extended state machine, in which the complete condition of the system (called the extended state) is the combination of a qualitative aspect—the state variable—and the quantitative aspects—the extended state variables.
The obvious advantage of extended state machines is flexibility. For example, changing the limit governed by key_count from 1000 to 10000 keystrokes, would not complicate the extended state machine at all. The only modification required would be changing the initialization value of the key_count extended state variable during initialization.
This flexibility of extended state machines comes with a price, however, because of the complex coupling between the "qualitative" and the "quantitative" aspects of the extended state. The coupling occurs through the guard conditions attached to transitions, as shown in Figure 2.
Guard conditions
Guard conditions (or simply guards) are Boolean expressions evaluated dynamically based on the value of extended state variables and event parameters. Guard conditions affect the behavior of a state machine by enabling actions or transitions only when they evaluate to TRUE and disabling them when they evaluate to FALSE. In the UML notation, guard conditions are shown in square brackets (e.g., in Figure 2).
The need for guards is the immediate consequence of adding memory extended state variables to the state machine formalism. Used sparingly, extended state variables and guards make up a powerful mechanism that can simplify designs. On the other hand, it is possible to abuse extended states and guards quite easily.
Actions and transitions
When an event instance is dispatched, the state machine responds by performing actions, such as changing a variable, performing I/O, invoking a function, generating another event instance, or changing to another state. Any parameter values associated with the current event are available to all actions directly caused by that event.
Switching from one state to another is called state transition, and the event that causes it is called the triggering event, or simply the trigger. In the keyboard example, if the keyboard is in the "default" state when the CapsLock key is pressed, the keyboard will enter the "caps_locked" state. However, if the keyboard is already in the "caps_locked" state, pressing CapsLock will cause a different transition—from the "caps_locked" to the "default" state. In both cases, pressing CapsLock is the triggering event.
In extended state machines, a transition can have a guard, which means that the transition can "fire" only if the guard evaluates to TRUE. A state can have many transitions in response to the same trigger, as long as they have nonoverlapping guards; however, this situation could create problems in the sequence of evaluation of the guards when the common trigger occurs. The UML specification intentionally does not stipulate any particular order; rather, UML puts the burden on the designer to devise guards in such a way that the order of their evaluation does not matter. Practically, this means that guard expressions should have no side effects, at least none that would alter evaluation of other guards having the same trigger.
Run-to-completion execution model
All state machine formalisms, including UML state machines, universally assume that a state machine completes processing of each event before it can start processing the next event. This model of execution is called run to completion, or RTC.
In the RTC model, the system processes events in discrete, indivisible RTC steps. New incoming events cannot interrupt the processing of the current event and must be stored (typically in an event queue) until the state machine becomes idle again. These semantics completely avoid any internal concurrency issues within a single state machine. The RTC model also gets around the conceptual problem of processing actions associated with transitions, where the state machine is not in a well-defined state (is between two states) for the duration of the action. During event processing, the system is unresponsive (unobservable), so the ill-defined state during that time has no practical significance.
Note, however, that RTC does not mean that a state machine has to monopolize the CPU until the RTC step is complete. The preemption restriction only applies to the task context of the state machine that is already busy processing events. In a multitasking environment, other tasks (not related to the task context of the busy state machine) can be running, possibly preempting the currently executing state machine. As long as other state machines do not share variables or other resources with each other, there are no concurrency hazards.
The key advantage of RTC processing is simplicity. Its biggest disadvantage is that the responsiveness of a state machine is determined by its longest RTC step. Achieving short RTC steps can often significantly complicate real-time designs.
UML extensions to the traditional FSM formalism
Though the traditional FSMs are an excellent tool for tackling smaller problems, it's also generally known that they tend to become unmanageable, even for moderately involved systems. Due to the phenomenon known as state and transition explosion, the complexity of a traditional FSM tends to grow much faster than the complexity of the system it describes. This happens because the traditional state machine formalism inflicts repetitions. For example, if you try to represent the behavior of a simple pocket calculator with a traditional FSM, you'll immediately notice that many events (e.g., the Clear or Off button presses) are handled identically in many states. A conventional FSM shown in the figure below, has no means of capturing such a commonality and requires repeating the same actions and transitions in many states. What's missing in the traditional state machines is the mechanism for factoring out the common behavior in order to share it across many states.
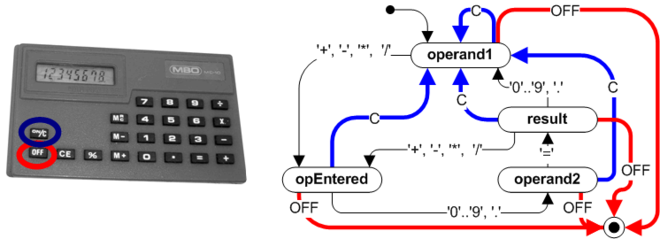
UML state machines address exactly this shortcoming of the conventional FSMs. They provide a number of features for eliminating the repetitions so that the complexity of a UML state machine no longer explodes but tends to faithfully represent the complexity of the reactive system it describes. Obviously, these features are very interesting to software developers, because only they make the whole state machine approach truly applicable to real-life problems.
Hierarchically nested states
The most important innovation of UML state machines over the traditional FSMs is the introduction of hierarchically nested states (that is why statecharts are also called hierarchical state machines, or HSMs). The semantics associated with state nesting are as follows (see Figure 3): If a system is in the nested state, for example "result" (called the substate), it also (implicitly) is in the surrounding state "on" (called the superstate). This state machine will attempt to handle any event in the context of the substate, which conceptually is at the lower level of the hierarchy. However, if the substate "result" does not prescribe how to handle the event, the event is not quietly discarded as in a traditional "flat" state machine; rather, it is automatically handled at the higher level context of the superstate "on". This is what is meant by the system being in state "result" as well as "on". Of course, state nesting is not limited to one level only, and the simple rule of event processing applies recursively to any level of nesting.

States that contain other states are called composite states; conversely, states without internal structure are called simple states. A nested state is called a direct substate when it is not contained by any other state; otherwise, it is referred to as a transitively nested substate.
Because the internal structure of a composite state can be arbitrarily complex, any hierarchical state machine can be viewed as an internal structure of some (higher-level) composite state. It is conceptually convenient to define one composite state as the ultimate root of state machine hierarchy. In the UML specification, every state machine has a region (the abstract root of every state machine hierarchy), which contains all the other elements of the entire state machine. The graphical rendering of this all-enclosing region is optional.
As you can see, the semantics of hierarchical state decomposition are designed to facilitate reusing of behavior. The substates (nested states) need only define the differences from the superstates (containing states). A substate can easily inherit the common behavior from its superstate(s) by simply ignoring commonly handled events, which are then automatically handled by higher-level states. In other words, hierarchical state nesting enables programming by difference.
The aspect of state hierarchy emphasized most often is abstraction—an old and powerful technique for coping with complexity. Instead of addressing all aspects of a complex system at the same time, it is often possible to ignore (abstract away) some parts of the system. Hierarchical states are an ideal mechanism for hiding internal details because the designer can easily zoom out or zoom in to hide or show nested states.
However, composite states don't simply hide complexity; they also actively reduce it through the powerful mechanism of hierarchical event processing. Without such reuse, even a moderate increase in system complexity could lead to an explosive increase in the number of states and transitions. For example, the hierarchical state machine representing the pocket calculator (Figure 3) avoids repeating the transitions Clear and Off in virtually every state. Avoiding repetition allows the growth of HSMs to remain proportionate to growth in system complexity. As the modeled system grows, the opportunity for reuse also increases and thus potentially counteracts the disproportionate increase in numbers of states and transitions typical of traditional FSMs.
Orthogonal regions
Analysis by hierarchical state decomposition can include the application of the operation 'exclusive-OR' to any given state. For example, if a system is in the "on" superstate (Figure 3), it may be the case that it is also in either "operand1" substate OR the "operand2" substate OR the "opEntered" substate OR the "result" substate. This would lead to description of the "on" superstate as an 'OR-state'.
UML statecharts also introduce the complementary AND-decomposition. Such decomposition means that a composite state can contain two or more orthogonal regions (orthogonal means compatible and independent in this context) and that being in such a composite state entails being in all its orthogonal regions simultaneously.
Orthogonal regions address the frequent problem of a combinatorial increase in the number of states when the behavior of a system is fragmented into independent, concurrently active parts. For example, apart from the main keypad, a computer keyboard has an independent numeric keypad. From the previous discussion, recall the two states of the main keypad already identified: "default" and "caps_locked" (see Figure 1). The numeric keypad also can be in two states—"numbers" and "arrows"—depending on whether Num Lock is active. The complete state space of the keyboard in the standard decomposition is therefore the Cartesian product of the two components (main keypad and numeric keypad) and consists of four states: "default–numbers," "default–arrows," "caps_locked–numbers," and "caps_locked–arrows." However, this would be an unnatural representation because the behavior of the numeric keypad does not depend on the state of the main keypad and vice versa. The use of orthogonal regions allows the mixing of independent behaviors as a Cartesian product to be avoided and, instead, for them to remain separate, as shown in Figure 4.

Note that if the orthogonal regions are fully independent of each other, their combined complexity is simply additive, which means that the number of independent states needed to model the system is simply the sum k + l + m + ..., where k, l, m, ... denote numbers of OR-states in each orthogonal region. However, the general case of mutual dependency, on the other hand, results in multiplicative complexity, so in general, the number of states needed is the product k × l × m × ....
In most real-life situations, orthogonal regions would be only approximately orthogonal (i.e. not truly independent). Therefore, UML statecharts provide a number of ways for orthogonal regions to communicate and synchronize their behaviors. Among these rich sets of (sometimes complex) mechanisms, perhaps the most important feature is that orthogonal regions can coordinate their behaviors by sending event instances to each other.
Even though orthogonal regions imply independence of execution (allowing more or less concurrency), the UML specification does not require that a separate thread of execution be assigned to each orthogonal region (although this can be done if desired). In fact, most commonly, orthogonal regions execute within the same thread. The UML specification requires only that the designer does not rely on any particular order for event instances to be dispatched to the relevant orthogonal regions.
Entry and exit actions
Every state in a UML statechart can have optional entry actions, which are executed upon entry to a state, as well as optional exit actions, which are executed upon exit from a state. Entry and exit actions are associated with states, not transitions. Regardless of how a state is entered or exited, all its entry and exit actions will be executed. Because of this characteristic, statecharts behave like Moore machines. The UML notation for state entry and exit actions is to place the reserved word "entry" (or "exit") in the state right below the name compartment, followed by the forward slash and the list of arbitrary actions (see Figure 5).

The value of entry and exit actions is that they provide means for guaranteed initialization and cleanup, very much like class constructors and destructors in Object-oriented programming. For example, consider the "door_open" state from Figure 5, which corresponds to the toaster oven behavior while the door is open. This state has a very important safety-critical requirement: Always disable the heater when the door is open. Additionally, while the door is open, the internal lamp illuminating the oven should light up.
Of course, such behavior could be modeled by adding appropriate actions (disabling the heater and turning on the light) to every transition path leading to the "door_open" state (the user may open the door at any time during "baking" or "toasting" or when the oven is not used at all). It should not be forgotten to extinguish the internal lamp with every transition leaving the "door_open" state. However, such a solution would cause the repetition of actions in many transitions. More importantly, such an approach leaves the design error-prone during subsequent amendments to behavior (e.g., the next programmer working on a new feature, such as top-browning, might simply forget to disable the heater on transition to "door_open").
Entry and exit actions allow implementation of desired behavior in a safer, simpler, and more intuitive way. As shown in Figure 5, it could be specified that the exit action from "heating" disables the heater, the entry action to "door_open" lights up the oven lamp, and the exit action from "door_open" extinguishes the lamp. The use of entry and exit actions is preferable to placing an action on a transition because it avoids repetitive coding and improves function by eliminating a safety hazard; (heater on while door open). The semantics of exit actions guarantees that, regardless of the transition path, the heater will be disabled when the toaster is not in the "heating" state.
Because entry actions are executed automatically whenever an associated state is entered, they often determine the conditions of operation or the identity of the state, very much as a class constructor determines the identity of the object being constructed. For example, the identity of the "heating" state is determined by the fact that the heater is turned on. This condition must be established before entering any substate of "heating" because entry actions to a substate of "heating," like "toasting," rely on proper initialization of the "heating" superstate and perform only the differences from this initialization. Consequently, the order of execution of entry actions must always proceed from the outermost state to the innermost state (top-down).
Not surprisingly, this order is analogous to the order in which class constructors are invoked. Construction of a class always starts at the very root of the class hierarchy and follows through all inheritance levels down to the class being instantiated. The execution of exit actions, which corresponds to destructor invocation, proceeds in the exact reverse order (bottom-up).
Internal transitions
Very commonly, an event causes only some internal actions to execute but does not lead to a change of state (state transition). In this case, all actions executed comprise the internal transition. For example, when one types on a keyboard, it responds by generating different character codes. However, unless the Caps Lock key is pressed, the state of the keyboard does not change (no state transition occurs). In UML, this situation should be modeled with internal transitions, as shown in Figure 6. The UML notation for internal transitions follows the general syntax used for exit (or entry) actions, except instead of the word entry (or exit) the internal transition is labeled with the triggering event (e.g., see the internal transition triggered by the ANY_KEY event in Figure 6).

In the absence of entry and exit actions, internal transitions would be identical to self-transitions (transitions in which the target state is the same as the source state). In fact, in a classical Mealy machine, actions are associated exclusively with state transitions, so the only way to execute actions without changing state is through a self-transition (depicted as a directed loop in Figure 1 from the top of this article). However, in the presence of entry and exit actions, as in UML statecharts, a self-transition involves the execution of exit and entry actions and therefore it is distinctively different from an internal transition.
In contrast to a self-transition, no entry or exit actions are ever executed as a result of an internal transition, even if the internal transition is inherited from a higher level of the hierarchy than the currently active state. Internal transitions inherited from superstates at any level of nesting act as if they were defined directly in the currently active state.
Transition execution sequence
State nesting combined with entry and exit actions significantly complicates the state transition semantics in HSMs compared to the traditional FSMs. When dealing with hierarchically nested states and orthogonal regions, the simple term current state can be quite confusing. In an HSM, more than one state can be active at once. If the state machine is in a leaf state that is contained in a composite state (which is possibly contained in a higher-level composite state, and so on), all the composite states that either directly or transitively contain the leaf state are also active. Furthermore, because some of the composite states in this hierarchy might have orthogonal regions, the current active state is actually represented by a tree of states starting with the single region at the root down to individual simple states at the leaves. The UML specification refers to such a state tree as state configuration.

In UML, a state transition can directly connect any two states. These two states, which may be composite, are designated as the main source and the main target of a transition. Figure 7 shows a simple transition example and explains the state roles in that transition. The UML specification prescribes that taking a state transition involves executing the actions in the following predefined sequence (see Section 14.2.3.9.6 of OMG Unified Modeling Language (OMG UML)):
- Evaluate the guard condition associated with the transition and perform the following steps only if the guard evaluates to TRUE.
- Exit the source state configuration.
- Execute the actions associated with the transition.
- Enter the target state configuration.
The transition sequence is easy to interpret in the simple case of both the main source and the main target nesting at the same level. For example, transition T1 shown in Figure 7 causes the evaluation of the guard g(); followed by the sequence of actions: a(); b(); t(); c(); d(); and e(); assuming that the guard g() evaluates to TRUE.
However, in the general case of source and target states nested at different levels of the state hierarchy, it might not be immediately obvious how many levels of nesting need to be exited. The UML specification prescribes that a transition involves exiting all nested states from the current active state (which might be a direct or transitive substate of the main source state) up to, but not including, the least common ancestor (LCA) state of the main source and main target states. As the name indicates, the LCA is the lowest composite state that is simultaneously a superstate (ancestor) of both the source and the target states. As described before, the order of execution of exit actions is always from the most deeply nested state (the current active state) up the hierarchy to the LCA but without exiting the LCA. For instance, the LCA(s1,s2) of states "s1" and "s2" shown in Figure 7 is state "s."
Entering the target state configuration commences from the level where the exit actions left off (i.e., from inside the LCA). As described before, entry actions must be executed starting from the highest-level state down the state hierarchy to the main target state. If the main target state is composite, the UML semantics prescribes to "drill" into its submachine recursively using the local initial transitions. The target state configuration is completely entered only after encountering a leaf state that has no initial transitions.
Local versus external transitions
Before UML 2, the only transition semantics in use was the external transition, in which the main source of the transition is always exited and the main target of the transition is always entered. UML 2 preserved the "external transition" semantics for backward compatibility, but introduced also a new kind of transition called local transition (see Section 14.2.3.4.4 of Unified Modeling Language (UML)). For many transition topologies, external and local transitions are actually identical. However, a local transition doesn't cause exit from and reentry to the main source state if the main target state is a substate of the main source. In addition, a local state transition doesn't cause exit from and reentry to the main target state if the main target is a superstate of the main source state.
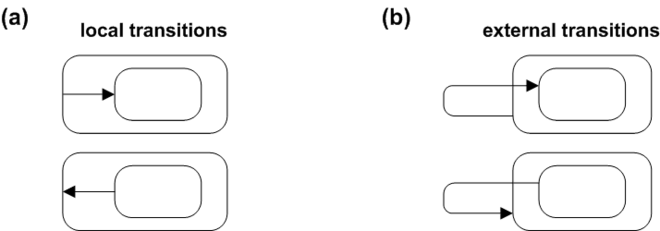
Figure 8 contrasts local (a) and external (b) transitions. In the top row, you see the case of the main source containing the main target. The local transition does not cause exit from the source, while the external transition causes exit and reentry to the source. In the bottom row of Figure 8, you see the case of the main target containing the main source. The local transition does not cause entry to the target, whereas the external transition causes exit and reentry to the target.
Event deferral
Sometimes an event arrives at a particularly inconvenient time, when a state machine is in a state that cannot handle the event. In many cases, the nature of the event is such that it can be postponed (within limits) until the system enters another state, in which it is better prepared to handle the original event.
UML state machines provide a special mechanism for deferring events in states. In every state, you can include a clause /defer. If an event in the current state's deferred event list occurs, the event will be saved (deferred) for future processing until a state is entered that does not list the event in its deferred event list. Upon entry to such a state, the UML state machine will automatically recall any saved event(s) that are no longer deferred and will then either consume or discard these events. It is possible for a superstate to have a transition defined on an event that is deferred by a substate. Consistent with other areas in the specification of UML state machines, the substate takes precedence over the superstate, the event will be deferred and the transition for the superstate will not be executed. In the case of orthogonal regions where one orthogonal region defers an event and another consumes the event, the consumer takes precedence and the event is consumed and not deferred.
The limitations of UML state machines
Harel statecharts, which are the precursors of UML state machines, have been invented as "a visual formalism for complex systems", so from their inception, they have been inseparably associated with graphical representation in the form of state diagrams. However, it is important to understand that the concept of UML state machine transcends any particular notation, graphical or textual. The UML specification makes this distinction apparent by clearly separating state machine semantics from the notation.
However, the notation of UML statecharts is not purely visual. Any nontrivial state machine requires a large amount of textual information (e.g., the specification of actions and guards). The exact syntax of action and guard expressions isn't defined in the UML specification, so many people use either structured English or, more formally, expressions in an implementation language such as C, C++, or Java. In practice, this means that UML statechart notation depends heavily on the specific programming language.
Nevertheless, most of the statecharts semantics are heavily biased toward graphical notation. For example, state diagrams poorly represent the sequence of processing, be it order of evaluation of guards or order of dispatching events to orthogonal regions. The UML specification sidesteps these problems by putting the burden on the designer not to rely on any particular sequencing. However, it is the case that when UML state machines are actually implemented, there is inevitably full control over order of execution, giving rise to criticism that the UML semantics may be unnecessarily restrictive. Similarly, statechart diagrams require a lot of plumbing gear (pseudostates, like joins, forks, junctions, choicepoints, etc.) to represent the flow of control graphically. In other words, these elements of the graphical notation do not add much value in representing flow of control as compared to plain structured code.
The UML notation and semantics are really geared toward computerized UML tools. A UML state machine, as represented in a tool, is not just the state diagram, but rather a mixture of graphical and textual representation that precisely captures both the state topology and the actions. The users of the tool can get several complementary views of the same state machine, both visual and textual, whereas the generated code is just one of the many available views.
References
- ^ "StateMachines". Unified Modeling Language 2.5.1. OMG Document Number formal/2017-12-05. Object Management Group Standards Development Organization (OMG SDO). December 2017. p. 305.
- ^ Harel, David (1987). "Statecharts: A Visual Formalism for Complex Systems" (PDF).
- D. Drusinsky, Modelling and verification using UML statecharts, Elsevier, 2006
- Samek, Miro (March 2009). "A crash course in UML state machines".
- Samek, Miro (2008). Practical UML Statecharts in C/C++, Second Edition: Event-Driven Programming for Embedded Systems. Newnes. p. 728. ISBN 978-0-7506-8706-5.
- ^ Samek, Miro (April 2003). "Who Moved My State?". C/C++ Users Journal, The Embedded Angle column.
- Selic, Bran; Gullekson, Garth; Ward, Paul T. (1994). Real-Time Object-Oriented Modeling. John Wiley & Sons. p. 525. ISBN 0-471-59917-4.
- Samek, Miro (August 2003). "Back to Basics". C/C++ Users Journal, The Embedded Angle column.
- "Region". Unified Modeling Language 2.5.1. OMG Document Number formal/2017-12-05. Object Management Group Standards Development Organization (OMG SDO). December 2017. p. 352.
- Samek, Miro (June 2003). "Dj Vu". C/C++ Users Journal, The Embedded Angle column. Archived from the original on 2012-09-30.
- Harel, David; Politi, Michal (1998). Modeling Reactive Systems with Statecharts, the STATEMATE Approach. McGraw-Hill. p. 258. ISBN 0-07-026205-5.
- Douglass, Bruce Powel (1999). Doing Hard Time: Developing Real-Time Systems with UML, Objects, Frameworks, and Patterns. Addison Wesley. p. 749. ISBN 0-201-49837-5.
- Douglass, Bruce Powel (January 1999). "UML Statecharts". Embedded Systems Programming.
External links
- Unified Modeling Language 2.5.1. OMG Document Number formal/2017-12-05. Object Management Group Standards Development Organization (OMG SDO). December 2017.
| Automata theory: formal languages and formal grammars | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
| Each category of languages, except those marked by a , is a proper subset of the category directly above it. Any language in each category is generated by a grammar and by an automaton in the category in the same line. | |||||||||
| Unified Modeling Language | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actors |
|  | |||||||||||
| Concepts |
| ||||||||||||
| Diagrams |
| ||||||||||||
| Derived languages | |||||||||||||
| Other topics | |||||||||||||