Hypsometry (from Ancient Greek ὕψος (húpsos) 'height' and μέτρον (métron) 'measure') is the measurement of the elevation and depth of features of Earth's surface relative to mean sea level.
On Earth, the elevations can take on either positive or negative (below sea level) values. The distribution is theorised to be bimodal due to the difference in density between the lighter continental crust and denser oceanic crust. On other planets within this solar system, elevations are typically unimodal, owing to the lack of plate tectonics on those bodies.
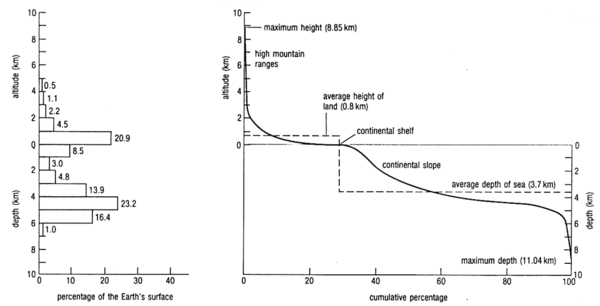
Hypsometric curve

A hypsometric curve is a histogram or cumulative distribution function of elevations in a geographical area. Differences in hypsometric curves between landscapes arise because the geomorphic processes that shape the landscape may be different.
When drawn as a 2-dimensional histogram, a hypsometric curve displays the elevation (y) on the vertical, y-axis and area above the corresponding elevation (x) on the horizontal or x-axis. The curve can also be shown in non-dimensional or standardized form by scaling elevation and area by the maximum values. The non-dimensional hypsometric curve provides a hydrologist or a geomorphologist with a way to assess the similarity of watersheds — and is one of several characteristics used for doing so. The hypsometric integral is a summary measure of the shape of the hypsometric curve.
In the original paper on this topic, Arthur Strahler proposed a curve containing three parameters to fit different hypsometric relations:
- ,
where a, d and z are fitting parameters. Subsequent research using two-dimensional landscape evolution models has called the general applicability of this fit into question, as well as the capability of the hypsometric curve to deal with scale-dependent effects. A modified curve with one additional parameter has been proposed to improve the fit.
Hypsometric curves are commonly used in limnology to represent the relationship between lake surface area and depth and calculate total lake volume. These graphs can be used to predict various characteristics of lakes such as productivity, dilution of incoming chemicals, and potential for water mixing.
See also
- Bathymetry
- Hypsometric equation
- Hypsometer, an instrument used in hypsometry, which estimates the elevation by boiling water – water boils at different temperatures depending on the air pressure, and thus altitude.
- Levelling
- Topography
- Orography
References
- ὕψος, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- μέτρον, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- Rafferty, John P. "Hypsometry". Encyclopedia Britannica. Retrieved 21 May 2021.
- The Editors of Encyclopaedia Britannica. "Hypsometric curve". Encyclopaedia Britannica. Retrieved 23 May 2021.
{{cite web}}:|last1=has generic name (help) - Strahler, Arthur N. (1952). "Hypsometric (area-altitude) analysis of erosional topography". Bulletin of the Geological Society of America. 63 (11): 1117–1142. Bibcode:1952GSAB...63.1117S. doi:10.1130/0016-7606(1952)63[1117:HAAOET]2.0.CO;2.
- Willgoose, G.; Hancock, G. (1998). "Revisiting the hypsometric curve as an indicator of form and process in transport‐limited catchment". Earth Surface Processes and Landforms. 23 (7): 611–623. Bibcode:1998ESPL...23..611W. doi:10.1002/(SICI)1096-9837(199807)23:7<611::AID-ESP872>3.0.CO;2-Y.
- Bajracharya, P.; Jain, S. (2021). "Characterization of drainage basin hypsometry: A generalized approach". Geomorphology. 381: 107645. Bibcode:2021Geomo.38107645B. doi:10.1016/j.geomorph.2021.107645. S2CID 233940229.
- Florida LAKEWATCH. "A Beginner's Guide to Water Management — Lake Morphometry" (PDF). Retrieved 17 December 2020.
 ,
,