Misplaced Pages

Interval propagation

Article snapshot taken from[REDACTED] with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.
Find sources: "Interval propagation" – news · newspapers · books · scholar · JSTOR (October 2013)

In numerical mathematics, interval propagation or interval constraint propagation is the problem of contracting interval domains associated to variables of R without removing any value that is consistent with a set of constraints (i.e., equations or inequalities). It can be used to propagate uncertainties in the situation where errors are represented by intervals. Interval propagation considers an estimation problem as a constraint satisfaction problem.

Atomic contractors

A contractor associated to an equation involving the variables x1,...,xn is an operator which contracts the intervals ,..., (that are supposed to enclose the xi's) without removing any value for the variables that is consistent with the equation.

A contractor is said to be atomic if it is not built as a composition of other contractors. The main theory that is used to build atomic contractors are based on interval analysis.

Example. Consider for instance the equation

x 1 + x 2 = x 3 , {\displaystyle x_{1}+x_{2}=x_{3},}

which involves the three variables x1,x2 and x3.

The associated contractor is given by the following statements

[ x 3 ] := [ x 3 ] ∩ ( [ x 1 ] + [ x 2 ] ) {\displaystyle :=\cap (+)}
[ x 1 ] := [ x 1 ] ∩ ( [ x 3 ] − [ x 2 ] ) {\displaystyle :=\cap (-)}
[ x 2 ] := [ x 2 ] ∩ ( [ x 3 ] − [ x 1 ] ) {\displaystyle :=\cap (-)}

For instance, if

x 1 ∈ [ − ∞ , 5 ] , {\displaystyle x_{1}\in ,}
x 2 ∈ [ − ∞ , 4 ] , {\displaystyle x_{2}\in ,}
x 3 ∈ [ 6 , ∞ ] {\displaystyle x_{3}\in }

the contractor performs the following calculus

x 3 = x 1 + x 2 ⇒ x 3 ∈ [ 6 , ∞ ] ∩ ( [ − ∞ , 5 ] + [ − ∞ , 4 ] ) = [ 6 , ∞ ] ∩ [ − ∞ , 9 ] = [ 6 , 9 ] . {\displaystyle x_{3}=x_{1}+x_{2}\Rightarrow x_{3}\in \cap (+)=\cap =.}
x 1 = x 3 − x 2 ⇒ x 1 ∈ [ − ∞ , 5 ] ∩ ( [ 6 , ∞ ] − [ − ∞ , 4 ] ) = [ − ∞ , 5 ] ∩ [ 2 , ∞ ] = [ 2 , 5 ] . {\displaystyle x_{1}=x_{3}-x_{2}\Rightarrow x_{1}\in \cap (-)=\cap =.}
x 2 = x 3 − x 1 ⇒ x 2 ∈ [ − ∞ , 4 ] ∩ ( [ 6 , ∞ ] − [ − ∞ , 5 ] ) = [ − ∞ , 4 ] ∩ [ 1 , ∞ ] = [ 1 , 4 ] . {\displaystyle x_{2}=x_{3}-x_{1}\Rightarrow x_{2}\in \cap (-)=\cap =.}
Figure 1: boxes before contraction
Figure 2: boxes after contraction

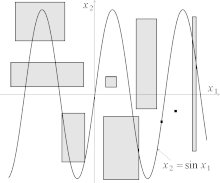
For other constraints, a specific algorithm for implementing the atomic contractor should be written. An illustration is the atomic contractor associated to the equation

x 2 = sin ⁡ ( x 1 ) , {\displaystyle x_{2}=\sin(x_{1}),}

is provided by Figures 1 and 2.

Decomposition

For more complex constraints, a decomposition into atomic constraints (i.e., constraints for which an atomic contractor exists) should be performed. Consider for instance the constraint

x + sin ⁡ ( x y ) ≤ 0 , {\displaystyle x+\sin(xy)\leq 0,}

could be decomposed into

a = x y {\displaystyle a=xy}
b = sin ⁡ ( a ) {\displaystyle b=\sin(a)}
c = x + b . {\displaystyle c=x+b.}

The interval domains that should be associated to the new intermediate variables are

a ∈ [ − ∞ , ∞ ] , {\displaystyle a\in ,}
b ∈ [ − 1 , 1 ] , {\displaystyle b\in ,}
c ∈ [ − ∞ , 0 ] . {\displaystyle c\in .}

Propagation

The principle of the interval propagation is to call all available atomic contractors until no more contraction could be observed. As a result of the Knaster-Tarski theorem, the procedure always converges to intervals which enclose all feasible values for the variables. A formalization of the interval propagation can be made thanks to the contractor algebra. Interval propagation converges quickly to the result and can deal with problems involving several hundred of variables.

Example

Consider the electronic circuit of Figure 3.

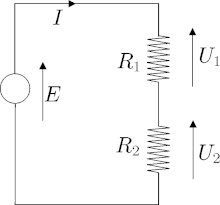
Figure 3: File:Electronic circuit to illustrate the interval propagation

Assume that from different measurements, we know that

E ∈ [ 23 V , 26 V ] {\displaystyle E\in }
I ∈ [ 4 A , 8 A ] {\displaystyle I\in }
U 1 ∈ [ 10 V , 11 V ] {\displaystyle U_{1}\in }
U 2 ∈ [ 14 V , 17 V ] {\displaystyle U_{2}\in }
P ∈ [ 124 W , 130 W ] {\displaystyle P\in }
R 1 ∈ [ 0 Ω , ∞ ] {\displaystyle R_{1}\in }
R 2 ∈ [ 0 Ω , ∞ ] . {\displaystyle R_{2}\in .}

From the circuit, we have the following equations

P = E I {\displaystyle P=EI}
U 1 = R 1 I {\displaystyle U_{1}=R_{1}I}
U 2 = R 2 I {\displaystyle U_{2}=R_{2}I}
E = U 1 + U 2 . {\displaystyle E=U_{1}+U_{2}.}

After performing the interval propagation, we get

E ∈ [ 24 V , 26 V ] {\displaystyle E\in }
I ∈ [ 4.769 A , 5.417 A ] {\displaystyle I\in }
U 1 ∈ [ 10 V , 11 V ] {\displaystyle U_{1}\in }
U 2 ∈ [ 14 V , 16 V ] {\displaystyle U_{2}\in }
P ∈ [ 124 W , 130 W ] {\displaystyle P\in }
R 1 ∈ [ 1.846 Ω , 2.307 Ω ] {\displaystyle R_{1}\in }
R 2 ∈ [ 2.584 Ω , 3.355 Ω ] . {\displaystyle R_{2}\in .}

References

  1. Jaulin, L.; Braems, I.; Walter, E. (2002). Interval methods for nonlinear identification and robust control (PDF). In Proceedings of the 41st IEEE Conference on Decision and Control (CDC).
  2. Cleary, J.L. (1987). Logical arithmetic. Future Computing Systems.
  3. Jaulin, L. (2006). Localization of an underwater robot using interval constraints propagation (PDF). In Proceedings of CP 2006.
Categories:
Interval propagation Add topic