
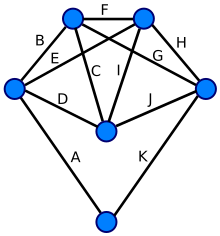
In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices). Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail that starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this:
- Given the graph in the image, is it possible to construct a path (or a cycle; i.e., a path starting and ending on the same vertex) that visits each edge exactly once?
Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have an Eulerian circuit. The first complete proof of this latter claim was published posthumously in 1873 by Carl Hierholzer. This is known as Euler's Theorem:
- A connected graph has an Euler cycle if and only if every vertex has an even number of incident edges.
The term Eulerian graph has two common meanings in graph theory. One meaning is a graph with an Eulerian circuit, and the other is a graph with every vertex of even degree. These definitions coincide for connected graphs.
For the existence of Eulerian trails it is necessary that zero or two vertices have an odd degree; this means the Königsberg graph is not Eulerian. If there are no vertices of odd degree, all Eulerian trails are circuits. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other. A graph that has an Eulerian trail but not an Eulerian circuit is called semi-Eulerian.
Definition
An Eulerian trail, or Euler walk, in an undirected graph is a walk that uses each edge exactly once. If such a walk exists, the graph is called traversable or semi-eulerian.
An Eulerian cycle, also called an Eulerian circuit or Euler tour, in an undirected graph is a cycle that uses each edge exactly once. If such a cycle exists, the graph is called Eulerian or unicursal. The term "Eulerian graph" is also sometimes used in a weaker sense to denote a graph where every vertex has even degree. For finite connected graphs the two definitions are equivalent, while a possibly unconnected graph is Eulerian in the weaker sense if and only if each connected component has an Eulerian cycle.
For directed graphs, "path" has to be replaced with directed path and "cycle" with directed cycle.
The definition and properties of Eulerian trails, cycles and graphs are valid for multigraphs as well.
An Eulerian orientation of an undirected graph G is an assignment of a direction to each edge of G such that, at each vertex v, the indegree of v equals the outdegree of v. Such an orientation exists for any undirected graph in which every vertex has even degree, and may be found by constructing an Euler tour in each connected component of G and then orienting the edges according to the tour. Every Eulerian orientation of a connected graph is a strong orientation, an orientation that makes the resulting directed graph strongly connected.
Properties
- An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
- An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
- An undirected graph has an Eulerian trail if and only if exactly zero or two vertices have odd degree, and all of its vertices with nonzero degree belong to a single connected component.
- A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.
- A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph.
Constructing Eulerian trails and circuits

- As the Haus vom Nikolaus puzzle has two odd-degree vertices (orange), the trail must start at one and end at the other.
- A variant with four odd-degree vertices has no solution.
- If there are no odd-degree vertices, the trail can start anywhere and forms an Eulerian cycle.
- Loose ends are considered vertices of degree 1.
- The graph must also be connected.
Fleury's algorithm
Fleury's algorithm is an elegant but inefficient algorithm that dates to 1883. Consider a graph known to have all edges in the same component and at most two vertices of odd degree. The algorithm starts at a vertex of odd degree, or, if the graph has none, it starts with an arbitrarily chosen vertex. At each step it chooses the next edge in the path to be one whose deletion would not disconnect the graph, unless there is no such edge, in which case it picks the remaining edge left at the current vertex. It then moves to the other endpoint of that edge and deletes the edge. At the end of the algorithm there are no edges left, and the sequence from which the edges were chosen forms an Eulerian cycle if the graph has no vertices of odd degree, or an Eulerian trail if there are exactly two vertices of odd degree.
While the graph traversal in Fleury's algorithm is linear in the number of edges, i.e. , we also need to factor in the complexity of detecting bridges. If we are to re-run Tarjan's linear time bridge-finding algorithm after the removal of every edge, Fleury's algorithm will have a time complexity of . A dynamic bridge-finding algorithm of Thorup (2000) allows this to be improved to , but this is still significantly slower than alternative algorithms.
Hierholzer's algorithm
Hierholzer's 1873 paper provides a different method for finding Euler cycles that is more efficient than Fleury's algorithm:
- Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
- As long as there exists a vertex u that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from u, following unused edges until returning to u, and join the tour formed in this way to the previous tour.
- Since we assume the original graph is connected, repeating the previous step will exhaust all edges of the graph.
By using a data structure such as a doubly linked list to maintain the set of unused edges incident to each vertex, to maintain the list of vertices on the current tour that have unused edges, and to maintain the tour itself, the individual operations of the algorithm (finding unused edges exiting each vertex, finding a new starting vertex for a tour, and connecting two tours that share a vertex) may be performed in constant time each, so the overall algorithm takes linear time, .
This algorithm may also be implemented with a deque. Because it is only possible to get stuck when the deque represents a closed tour, one should rotate the deque by removing edges from the tail and adding them to the head until unstuck, and then continue until all edges are accounted for. This also takes linear time, as the number of rotations performed is never larger than (intuitively, any "bad" edges are moved to the head, while fresh edges are added to the tail)

Counting Eulerian circuits
Complexity issues
The number of Eulerian circuits in digraphs can be calculated using the so-called BEST theorem, named after de Bruijn, van Aardenne-Ehrenfest, Smith and Tutte. The formula states that the number of Eulerian circuits in a digraph is the product of certain degree factorials and the number of rooted arborescences. The latter can be computed as a determinant, by the matrix tree theorem, giving a polynomial time algorithm.
BEST theorem is first stated in this form in a "note added in proof" to the Aardenne-Ehrenfest and de Bruijn paper (1951). The original proof was bijective and generalized the de Bruijn sequences. It is a variation on an earlier result by Smith and Tutte (1941).
Counting the number of Eulerian circuits on undirected graphs is much more difficult. This problem is known to be #P-complete. In a positive direction, a Markov chain Monte Carlo approach, via the Kotzig transformations (introduced by Anton Kotzig in 1968) is believed to give a sharp approximation for the number of Eulerian circuits in a graph, though as yet there is no proof of this fact (even for graphs of bounded degree).
Special cases
An asymptotic formula for the number of Eulerian circuits in the complete graphs was determined by McKay and Robinson (1995):
A similar formula was later obtained by M.I. Isaev (2009) for complete bipartite graphs:
Applications
Eulerian trails are used in bioinformatics to reconstruct the DNA sequence from its fragments. They are also used in CMOS circuit design to find an optimal logic gate ordering. There are some algorithms for processing trees that rely on an Euler tour of the tree (where each edge is treated as a pair of arcs). The de Bruijn sequences can be constructed as Eulerian trails of de Bruijn graphs.
In infinite graphs

In an infinite graph, the corresponding concept to an Eulerian trail or Eulerian cycle is an Eulerian line, a doubly-infinite trail that covers all of the edges of the graph. It is not sufficient for the existence of such a trail that the graph be connected and that all vertex degrees be even; for instance, the infinite Cayley graph shown, with all vertex degrees equal to four, has no Eulerian line. The infinite graphs that contain Eulerian lines were characterized by Erdõs, Grünwald & Weiszfeld (1936). For an infinite graph or multigraph G to have an Eulerian line, it is necessary and sufficient that all of the following conditions be met:
- G is connected.
- G has countable sets of vertices and edges.
- G has no vertices of (finite) odd degree.
- Removing any finite subgraph S from G leaves at most two infinite connected components in the remaining graph, and if S has even degree at each of its vertices then removing S leaves exactly one infinite connected component.
Undirected Eulerian graphs
Euler stated a necessary condition for a finite graph to be Eulerian as all vertices must have even degree. Hierholzer proved this is a sufficient condition in a paper published in 1873. This leads to the following necessary and sufficient statement for what a finite graph must have to be Eulerian: An undirected connected finite graph is Eulerian if and only if every vertex of G has even degree.
The following result was proved by Veblen in 1912: An undirected connected graph is Eulerian if and only if it is the disjoint union of some cycles.

Hierholzer developed a linear time algorithm for constructing an Eulerian tour in an undirected graph.
Directed Eulerian graphs
It is possible to have a directed graph that has all even out-degrees but is not Eulerian. Since an Eulerian circuit leaves a vertex the same number of times as it enters that vertex, a necessary condition for an Eulerian circuit to exist is that the in-degree and out-degree are equal at each vertex. Obviously, connectivity is also necessary. König proved that these conditions are also sufficient. That is, a directed graph is Eulerian if and only if it is connected and the in-degree and out-degree are equal at each vertex.
In this theorem it doesn't matter whether "connected" means "weakly connected" or "strongly connected" since they are equivalent for Eulerian graphs.
Hierholzer's linear time algorithm for constructing an Eulerian tour is also applicable to directed graphs.
Mixed Eulerian graphs
All mixed graphs that are both even and symmetric are guaranteed to be Eulerian. However, this is not a necessary condition, as it is possible to construct a non-symmetric, even graph that is Eulerian.
Ford and Fulkerson proved in 1962 in their book Flows in Networks a necessary and sufficient condition for a graph to be Eulerian, viz., that every vertex must be even and satisfy the balance condition, i.e. for every subset of vertices S, the difference between the number of arcs leaving S and entering S must be less than or equal to the number of edges incident with S.
The process of checking if a mixed graph is Eulerian is harder than checking if an undirected or directed graph is Eulerian because the balanced set condition concerns every possible subset of vertices.


See also
- Eulerian matroid, an abstract generalization of Eulerian graphs
- Five room puzzle
- Handshaking lemma, proven by Euler in his original paper, showing that any undirected connected graph has an even number of odd-degree vertices
- Hamiltonian path – a path that visits each vertex exactly once.
- Route inspection problem, search for the shortest path that visits all edges, possibly repeating edges if an Eulerian path does not exist.
- Veblen's theorem, which states that graphs with even vertex degree can be partitioned into edge-disjoint cycles regardless of their connectivity
Notes
- ^ Some people reserve the terms path and cycle to mean non-self-intersecting path and cycle. A (potentially) self-intersecting path is known as a trail or an open walk; and a (potentially) self-intersecting cycle, a circuit or a closed walk. This ambiguity can be avoided by using the terms Eulerian trail and Eulerian circuit when self-intersection is allowed.
References
- N. L. Biggs, E. K. Lloyd and R. J. Wilson, Graph Theory, 1736–1936, Clarendon Press, Oxford, 1976, 8–9, ISBN 0-19-853901-0.
- C. L. Mallows, N. J. A. Sloane (1975). "Two-graphs, switching classes and Euler graphs are equal in number" (PDF). SIAM Journal on Applied Mathematics. 28 (4): 876–880. doi:10.1137/0128070. JSTOR 2100368.
- Jun-ichi Yamaguchi, Introduction of Graph Theory.
- Schaum's outline of theory and problems of graph theory By V. K. Balakrishnan .
- Schrijver, A. (1983), "Bounds on the number of Eulerian orientations", Combinatorica, 3 (3–4): 375–380, doi:10.1007/BF02579193, MR 0729790, S2CID 13708977.
- ^ Pólya, George; Tarjan, Robert E.; Woods, Donald R. (October 2009), "Hamiltonian and Eulerian Paths", Notes on Introductory Combinatorics, Birkhäuser Boston, pp. 157–168, doi:10.1007/978-0-8176-4953-1_13, ISBN 9780817649531
- Fleury, Pierre-Henry (1883), "Deux problèmes de Géométrie de situation", Journal de mathématiques élémentaires, 2nd ser. (in French), 2: 257–261.
- Tarjan, R. Endre (1974), "A note on finding the bridges of a graph", Information Processing Letters, 2 (6): 160–161, doi:10.1016/0020-0190(74)90003-9, MR 0349483.
- Fleischner, Herbert (1991), "X.1 Algorithms for Eulerian Trails", Eulerian Graphs and Related Topics: Part 1, Volume 2, Annals of Discrete Mathematics, vol. 50, Elsevier, pp. X.1–13, ISBN 978-0-444-89110-5.
- Brightwell and Winkler, "Note on Counting Eulerian Circuits", 2004.
- Brendan McKay and Robert W. Robinson, Asymptotic enumeration of eulerian circuits in the complete graph, Combinatorica, 10 (1995), no. 4, 367–377.
- M.I. Isaev (2009). "Asymptotic number of Eulerian circuits in complete bipartite graphs". Proc. 52-nd MFTI Conference (in Russian). Moscow: 111–114.
- Pevzner, Pavel A.; Tang, Haixu; Waterman, Michael S. (2001). "An Eulerian trail approach to DNA fragment assembly". Proceedings of the National Academy of Sciences of the United States of America. 98 (17): 9748–9753. Bibcode:2001PNAS...98.9748P. doi:10.1073/pnas.171285098. PMC 55524. PMID 11504945.
- Roy, Kuntal (2007). "Optimum Gate Ordering of CMOS Logic Gates Using Euler Path Approach: Some Insights and Explanations". Journal of Computing and Information Technology. 15 (1): 85–92. doi:10.2498/cit.1000731.
- Tarjan, Robert E.; Vishkin, Uzi (1985). "An efficient parallel biconnectivity algorithm". SIAM Journal on Computing. 14 (4): 862–874. CiteSeerX 10.1.1.465.8898. doi:10.1137/0214061.
- Berkman, Omer; Vishkin, Uzi (Apr 1994). "Finding level-ancestors in trees". J. Comput. Syst. Sci. 2. 48 (2): 214–230. doi:10.1016/S0022-0000(05)80002-9.
- Savage, Carla (January 1997). "A Survey of Combinatorial Gray Codes". SIAM Review. 39 (4): 605–629. doi:10.1137/S0036144595295272. ISSN 0036-1445.
- Komjáth, Peter (2013), "Erdős's work on infinite graphs", Erdös centennial, Bolyai Soc. Math. Stud., vol. 25, János Bolyai Math. Soc., Budapest, pp. 325–345, doi:10.1007/978-3-642-39286-3_11, MR 3203602.
- Bollobás, Béla (1998), Modern graph theory, Graduate Texts in Mathematics, vol. 184, Springer-Verlag, New York, p. 20, doi:10.1007/978-1-4612-0619-4, ISBN 0-387-98488-7, MR 1633290.
- ^ Corberán, Ángel; Laporte, Gilbert, eds. (2015). Arc Routing: Problems, Methods, and Applications. MOS-SIAM Series on Optimization. SIAM. doi:10.1137/1.9781611973679. ISBN 978-1-61197-366-2. Retrieved 2022-08-19.
Bibliography
- Erdõs, Pál; Grünwald, Tibor; Weiszfeld, Endre (1936), "Végtelen gráfok Euler vonalairól" [On Euler lines of infinite graphs] (PDF), Mat. Fix. Lapok (in Hungarian), 43: 129–140. Translated as Erdős, P.; Grünwald, T.; Vázsonyi, E. (1938), "Über Euler-Linien unendlicher Graphen" [On Eulerian lines in infinite graphs] (PDF), J. Math. Phys. (in German), 17 (1–4): 59–75, doi:10.1002/sapm193817159.
- Euler, L., "Solutio problematis ad geometriam situs pertinentis", Comment. Academiae Sci. I. Petropolitanae 8 (1736), 128–140.
- Hierholzer, Carl (1873), "Ueber die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren", Mathematische Annalen, 6 (1): 30–32, doi:10.1007/BF01442866, S2CID 119885172.
- Lucas, E., Récréations Mathématiques IV, Paris, 1921.
- Fleury, "Deux problemes de geometrie de situation", Journal de mathematiques elementaires (1883), 257–261.
- T. van Aardenne-Ehrenfest and N. G. de Bruijn (1951) "Circuits and trees in oriented linear graphs", Simon Stevin 28: 203–217.
- Thorup, Mikkel (2000), "Near-optimal fully-dynamic graph connectivity", Proc. 32nd ACM Symposium on Theory of Computing, pp. 343–350, doi:10.1145/335305.335345, S2CID 128282
- W. T. Tutte and C. A. B. Smith (1941) "On Unicursal Paths in a Network of Degree 4", American Mathematical Monthly 48: 233–237.
 , we also need to factor in the complexity of detecting
, we also need to factor in the complexity of detecting  . A dynamic bridge-finding algorithm of
. A dynamic bridge-finding algorithm of  , but this is still significantly slower than alternative algorithms.
, but this is still significantly slower than alternative algorithms.
 (intuitively, any "bad" edges are moved to the head, while fresh edges are added to the tail)
(intuitively, any "bad" edges are moved to the head, while fresh edges are added to the tail)

