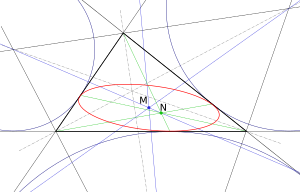
In geometry, the Mandart inellipse of a triangle is an ellipse that is inscribed within the triangle, tangent to its sides at the contact points of its excircles (which are also the vertices of the extouch triangle and the endpoints of the splitters). The Mandart inellipse is named after H. Mandart, who studied it in two papers published in the late 19th century.
Parameters
As an inconic, the Mandart inellipse is described by the parameters
where a, b, and c are sides of the given triangle.
Related points
The center of the Mandart inellipse is the mittenpunkt of the triangle. The three lines connecting the triangle vertices to the opposite points of tangency all meet in a single point, the Nagel point of the triangle.
See also
- Steiner inellipse, a different ellipse tangent to a triangle at the midpoints of its sides
Notes
- Juhász, Imre (2012), "Control point based representation of inellipses of triangles" (PDF), Annales Mathematicae et Informaticae, 40: 37–46, MR 3005114.
- ^ Gibert, Bernard (2004), "Generalized Mandart conics" (PDF), Forum Geometricorum, 4: 177–198.
- Mandart, H. (1893), "Sur l'hyperbole de Feuerbach", Mathesis: 81–89; Mandart, H. (1894), "Sur une ellipse associée au triangle", Mathesis: 241–245. As cited by Gibert (2004).
