| This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources. Find sources: "Logical biconditional" – news · newspapers · books · scholar · JSTOR (June 2013) |
| Logical connectives | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||
| Related concepts | ||||||||||||||||||||||||||
| Applications | ||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||
(true part in red)
In logic and mathematics, the logical biconditional, also known as material biconditional or equivalence or biimplication or bientailment, is the logical connective used to conjoin two statements and to form the statement " if and only if " (often abbreviated as " iff "), where is known as the antecedent, and the consequent.
Nowadays, notations to represent equivalence include .
is logically equivalent to both and , and the XNOR (exclusive nor) Boolean operator, which means "both or neither".
Semantically, the only case where a logical biconditional is different from a material conditional is the case where the hypothesis (antecedent) is false but the conclusion (consequent) is true. In this case, the result is true for the conditional, but false for the biconditional.
In the conceptual interpretation, P = Q means "All P's are Q's and all Q's are P's". In other words, the sets P and Q coincide: they are identical. However, this does not mean that P and Q need to have the same meaning (e.g., P could be "equiangular trilateral" and Q could be "equilateral triangle"). When phrased as a sentence, the antecedent is the subject and the consequent is the predicate of a universal affirmative proposition (e.g., in the phrase "all men are mortal", "men" is the subject and "mortal" is the predicate).
In the propositional interpretation, means that P implies Q and Q implies P; in other words, the propositions are logically equivalent, in the sense that both are either jointly true or jointly false. Again, this does not mean that they need to have the same meaning, as P could be "the triangle ABC has two equal sides" and Q could be "the triangle ABC has two equal angles". In general, the antecedent is the premise, or the cause, and the consequent is the consequence. When an implication is translated by a hypothetical (or conditional) judgment, the antecedent is called the hypothesis (or the condition) and the consequent is called the thesis.
A common way of demonstrating a biconditional of the form is to demonstrate that and separately (due to its equivalence to the conjunction of the two converse conditionals). Yet another way of demonstrating the same biconditional is by demonstrating that and .
When both members of the biconditional are propositions, it can be separated into two conditionals, of which one is called a theorem and the other its reciprocal. Thus whenever a theorem and its reciprocal are true, we have a biconditional. A simple theorem gives rise to an implication, whose antecedent is the hypothesis and whose consequent is the thesis of the theorem.
It is often said that the hypothesis is the sufficient condition of the thesis, and that the thesis is the necessary condition of the hypothesis. That is, it is sufficient that the hypothesis be true for the thesis to be true, while it is necessary that the thesis be true if the hypothesis were true. When a theorem and its reciprocal are true, its hypothesis is said to be the necessary and sufficient condition of the thesis. That is, the hypothesis is both the cause and the consequence of the thesis at the same time.
Notations
Notations to represent equivalence used in history include:
- in George Boole in 1847. Although Boole used mainly on classes, he also considered the case that are propositions in , and at the time is equivalence.
- in Frege in 1879;
- in Bernays in 1918;
- in Hilbert in 1927 (while he used as the main symbol in the article);
- in Hilbert and Ackermann in 1928 (they also introduced while they use as the main symbol in the whole book; is adopted by many followers such as Becker in 1933);
- (prefix) in Łukasiewicz in 1929 and (prefix) in Łukasiewicz in 1951;
- in Heyting in 1930;
- in Bourbaki in 1954;
- in Chazal in 1996;
and so on. Somebody else also use or occasionally.
Definition
Logical equality (also known as biconditional) is an operation on two logical values, typically the values of two propositions, that produces a value of true if and only if both operands are false or both operands are true.
Truth table
The following is a truth table for :
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
When more than two statements are involved, combining them with might be ambiguous. For example, the statement
may be interpreted as
- ,
or may be interpreted as saying that all xi are jointly true or jointly false:
As it turns out, these two statements are only the same when zero or two arguments are involved. In fact, the following truth tables only show the same bit pattern in the line with no argument and in the lines with two arguments:

meant as equivalent to
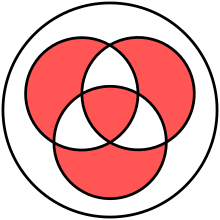
The central Venn diagram below,
and line (ABC ) in this matrix
represent the same operation.
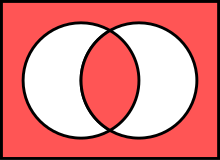
meant as shorthand for
The Venn diagram directly below,
and line (ABC ) in this matrix
represent the same operation.
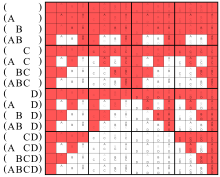
The left Venn diagram below, and the lines (AB ) in these matrices represent the same operation.
Venn diagrams
Red areas stand for true (as in ![]() for and).
for and).
|
|
|
Properties
Commutativity: Yes
Associativity: Yes

|

|
|

|

|
Distributivity: Biconditional doesn't distribute over any binary function (not even itself), but logical disjunction distributes over biconditional.
Idempotency: No
Monotonicity: No

|

|

|

|
Truth-preserving: Yes
When all inputs are true, the output is true.
Falsehood-preserving: No
When all inputs are false, the output is not false.
Walsh spectrum: (2,0,0,2)
Nonlinearity: 0 (the function is linear)
Rules of inference
Main article: Rules of inferenceLike all connectives in first-order logic, the biconditional has rules of inference that govern its use in formal proofs.
Biconditional introduction
Main article: Biconditional introductionBiconditional introduction allows one to infer that if B follows from A and A follows from B, then A if and only if B.
For example, from the statements "if I'm breathing, then I'm alive" and "if I'm alive, then I'm breathing", it can be inferred that "I'm breathing if and only if I'm alive" or equivalently, "I'm alive if and only if I'm breathing." Or more schematically:
B → A A → B ∴ A ↔ B
B → A A → B ∴ B ↔ A
Biconditional elimination
Biconditional elimination allows one to infer a conditional from a biconditional: if A ↔ B is true, then one may infer either A → B, or B → A.
For example, if it is true that I'm breathing if and only if I'm alive, then it's true that if I'm breathing, then I'm alive; likewise, it's true that if I'm alive, then I'm breathing. Or more schematically:
A ↔ B ∴ A → B
A ↔ B ∴ B → A
Colloquial usage
One unambiguous way of stating a biconditional in plain English is to adopt the form "b if a and a if b"—if the standard form "a if and only if b" is not used. Slightly more formally, one could also say that "b implies a and a implies b", or "a is necessary and sufficient for b". The plain English "if'" may sometimes be used as a biconditional (especially in the context of a mathematical definition). In which case, one must take into consideration the surrounding context when interpreting these words.
For example, the statement "I'll buy you a new wallet if you need one" may be interpreted as a biconditional, since the speaker doesn't intend a valid outcome to be buying the wallet whether or not the wallet is needed (as in a conditional). However, "it is cloudy if it is raining" is generally not meant as a biconditional, since it can still be cloudy even if it is not raining.
See also
- If and only if
- Logical equivalence
- Logical equality
- XNOR gate
- Biconditional elimination
- Biconditional introduction
References
- Weisstein, Eric W. "Iff". mathworld.wolfram.com. Retrieved 2019-11-25.
- ^ Peil, Timothy. "Conditionals and Biconditionals". web.mnstate.edu. Archived from the original on 2020-10-24. Retrieved 2019-11-25.
- Brennan, Joseph G. (1961). Handbook of Logic (2nd ed.). Harper & Row. p. 81.
- Boole, G. (1847). The Mathematical Analysis of Logic, Being an Essay Towards a Calculus of Deductive Reasoning. Cambridge/London: Macmillan, Barclay, & Macmillan/George Bell. p. 17.
- Frege, G. (1879). Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens (in German). Halle a/S.: Verlag von Louis Nebert. p. 15.
- Bernays, P. (1918). Beiträge zur axiomatischen Behandlung des Logik-Kalküls. Göttingen: Universität Göttingen. p. 3.
- Hilbert, D. (1928) . "Die Grundlagen der Mathematik". Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität (in German). 6: 65–85. doi:10.1007/BF02940602.
- Hilbert, D.; Ackermann, W. (1928). Grundzügen der theoretischen Logik (in German) (1 ed.). Berlin: Verlag von Julius Springer. p. 4.
- Becker, A. (1933). Die Aristotelische Theorie der Möglichkeitsschlösse: Eine logisch-philologische Untersuchung der Kapitel 13-22 von Aristoteles' Analytica priora I (in German). Berlin: Junker und Dünnhaupt Verlag. p. 4.
- Łukasiewicz, J. (1958) . Słupecki, J. (ed.). Elementy logiki matematycznej (in Polish) (2 ed.). Warszawa: Państwowe Wydawnictwo Naukowe.
- Łukasiewicz, J. (1957) . Słupecki, J. (ed.). Aristotle's Syllogistic from the Standpoint of Modern Formal Logic (in Polish) (2 ed.). Glasgow, New York, Toronto, Melbourne, Wellington, Bombay, Calcutta, Madras, Karachi, Lahore, Dacca, Cape Town, Salisbury, Nairobi, Ibadan, Accra, Kuala Lumpur and Hong Kong: Oxford University Press.
- Heyting, A. (1930). "Die formalen Regeln der intuitionistischen Logik". Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse (in German): 42–56.
- Bourbaki, N. (1954). Théorie des ensembles (in French). Paris: Hermann & Cie, Éditeurs. p. 32.
- Chazal, G. (1996). Eléments de logique formelle. Paris: Hermes Science Publications.
- In fact, such is the style adopted by Misplaced Pages's manual of style in mathematics.
External links
- [REDACTED] Media related to Logical biconditional at Wikimedia Commons
| Common logical connectives | ||
|---|---|---|
 | ||
| Mathematical logic | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems (list) and paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Formal systems (list), language and syntax |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||
This article incorporates material from Biconditional on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
Categories:













 and
and  to form the statement "
to form the statement " .
.
 and
and  , and the
, and the  and
and  separately (due to its equivalence to the conjunction of the two converse
separately (due to its equivalence to the conjunction of the two converse  .
.
 in
in  are propositions in
are propositions in  , and at the time
, and at the time  in
in  in
in  in
in  in
in  while they use
while they use  (prefix) in
(prefix) in  in
in  in
in  in Chazal in 1996;
in Chazal in 1996; or
or  occasionally.
occasionally.
 :
:



 ,
,