In biochemistry, the Monod–Wyman–Changeux model (MWC model, also known as the symmetry model or concerted model) describes allosteric transitions of proteins made up of identical subunits. It was proposed by Jean-Pierre Changeux in his PhD thesis, and described by Jacques Monod, Jeffries Wyman, and Jean-Pierre Changeux. It contrasts with the sequential model and substrate presentation.
The concept of two distinct symmetric states is the central postulate of the MWC model. The main idea is that regulated proteins, such as many enzymes and receptors, exist in different interconvertible states in the absence of any regulator. The ratio of the different conformational states is determined by thermal equilibrium. This model is defined by the following rules:
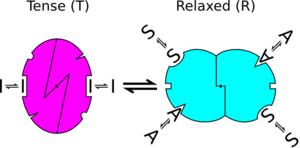
- An allosteric protein is an oligomer of protomers that are symmetrically related (for hemoglobin, we shall assume, for the sake of algebraic simplicity, that all four subunits are functionally identical).
- Each protomer can exist in (at least) two conformational states, designated T and R; these states are in equilibrium whether or not ligand is bound to the oligomer.
- The ligand can bind to a protomer in either conformation. Only the conformational change alters the affinity of a protomer for the ligand. The regulators merely shift the equilibrium toward one state or another. For instance, an agonist will stabilize the active form of a pharmacological receptor. Phenomenologically, it looks as if the agonist provokes the conformational transition. One crucial feature of the model is the dissociation between the binding function (the fraction of protein bound to the regulator), and the state function (the fraction of protein under the activated state), cf below. In the models said of "induced-fit", those functions are identical.
In the historical model, each allosteric unit, called a protomer (generally assumed to be a subunit), can exist in two different conformational states – designated 'R' (for relaxed) or 'T' (for tense) states. In any one molecule, all protomers must be in the same state. That is to say, all subunits must be in either the R or the T state. Proteins with subunits in different states are not allowed by this model. The R state has a higher affinity for the ligand than the T state. Because of that, although the ligand may bind to the subunit when it is in either state, the binding of a ligand will increase the equilibrium in favor of the R state.
Two equations can be derived, that express the fractional occupancy of the ligand binding site () and the fraction of the proteins in the R state ():
Where is the allosteric constant, that is the ratio of proteins in the T and R states in the absence of ligand, is the ratio of the affinities of R and T states for the ligand, and , the normalized concentration of ligand. It is not immediately obvious that the expression for is a form of the Adair equation, but in fact it is, as one can see by multiplying out the expressions in parentheses and comparing the coefficients of powers of with corresponding coefficients in the Adair equation.
This model explains sigmoidal binding properties (i.e. positive cooperativity) as change in concentration of ligand over a small range will lead to a large increase in the proportion of molecules in the R state, and thus will lead to a high association of the ligand to the protein. It cannot explain negative cooperativity.
The MWC model proved very popular in enzymology, and pharmacology, although it has been shown inappropriate in a certain number of cases. The best example of a successful application of the model is the regulation of hemoglobin function. Extensions of the model have been proposed for lattices of proteins by various authors. Edelstein argued that the MWC model gave a better account of the data for hemoglobin than the sequential model could do. He and Changeux applied the model to signal transduction. Changeux has discussed the status of the model after 50 years.
See also
References
- Monod, J; Wyman, J; Changeux, J.-P. (1965). "On the Nature of Allosteric Transitions — a Plausible Model". J. Mol. Biol. 12 (1): 88–118. doi:10.1016/S0022-2836(65)80285-6. PMID 14343300.
- Changeux, J.-P. (1964). "Allosteric interactions interpreted in terms of quaternary structure". Brookhaven Symp. Biol. 17: 232–249. PMID 14246265.
- ^ Koshland, D.E. Jr.; Némethy, G.; Filmer, D. (1966). "Comparison of Experimental Binding Data and Theoretical Models in Proteins Containing Subunits". Biochemistry. 5 (1): 365–385. doi:10.1021/Bi00865A047. PMID 5938952.
- Cornish-Bowden, A. Fundamentals of Enzyme Kinetics (4th ed.). Weinheim, Germany: Wiley-Blackwell. pp. 306–310.
- Changeux, J.-P.; Thiery, J.; Tung, Y.; Kittel, C. (1967). "On the Cooperativity Of Biological Membranes". Proc. Natl. Acad. Sci. USA. 57 (2): 335–341. doi:10.1073/Pnas.57.2.335. PMC 335510. PMID 16591474.
- Wyman, J/ (1969). "Possible Allosteric Effects in Extended Biological Systems". J. Mol. Biol. 39 (3): 523–538. doi:10.1016/0022-2836(69)90142-9. PMID 5357210.
- Duke, T.A.J.; Le Novère, N.; Bray, D. (2001). "Conformational spread in a ring of proteins: A stochastic approach to allostery". J. Mol. Biol. 308 (3): 541–553. doi:10.1006/jmbi.2001.4610. PMID 11327786.
- Edelstein, S.J. (1971). "Extensions of Allosteric Model for Haemoglobin". Nature. 230 (5291): 224–227. doi:10.1038/230224A0. PMID 4926711. S2CID 4201272.
- Changeux, J.-P.; Edelstein, S.J. (2005). "Allosteric mechanisms of signal transduction". Science. 308 (5727): 1424–1428. doi:10.1126/science.1108595. PMID 15933191. S2CID 10621930.
- Changeux, Jean-Pierre (2012). "Allostery and the Monod-Wyman-Changeux Model After 50 Years". Annual Review of Biophysics. 41 (1): 103–133. doi:10.1146/annurev-biophys-050511-102222. PMID 22224598. S2CID 25909068.
 ) and the fraction of the proteins in the R state (
) and the fraction of the proteins in the R state ( ):
):


 is the allosteric constant, that is the ratio of proteins in the T and R states in the absence of ligand,
is the allosteric constant, that is the ratio of proteins in the T and R states in the absence of ligand,  is the ratio of the affinities of R and T states for the ligand, and
is the ratio of the affinities of R and T states for the ligand, and  , the normalized concentration of ligand. It is not immediately obvious that the expression for
, the normalized concentration of ligand. It is not immediately obvious that the expression for  with corresponding
with corresponding  coefficients in the Adair equation.
coefficients in the Adair equation.