In computer science, an oblivious data structure is a data structure that gives no information about the sequence or pattern of the operations that have been applied except for the final result of the operations.
In most conditions, even if the data is encrypted, the access pattern can be achieved, and this pattern can leak some important information such as encryption keys. And in the outsourcing of cloud data, this leakage of access pattern is still very serious. An access pattern is a specification of an access mode for every attribute of a relation schema. For example, the sequences of user read or write the data in the cloud are access patterns.
We say a machine is oblivious if the sequence in which it accesses is equivalent for any two inputs with the same running time. So the data access pattern is independent from the input.
Applications:
- Cloud data outsourcing: When writing or reading data from a cloud server, oblivious data structures are useful. And modern databases rely on data structures heavily, so oblivious data structures come in handy.
- Secure processor: Tamper-resilient secure processors are used for defense against physical attacks or the malicious intruders access the users’ computer platforms. The existing secure processors designed in academia and industry include AEGIS and Intel SGX. But the memory addresses are still transferred in the clear on the memory bus. So the research finds that this memory buses can give out the information about encryption keys. With the Oblivious data structure comes in practical, the secure processor can obfuscate memory access pattern in a provably secure manner.
- Secure computation: Traditionally people used circuit-model to do the secure computation, but the model is not enough for the security when the amount of data is getting big. RAM-model secure computation was proposed as an alternative to the traditional circuit model, and oblivious data structure is used to prevent information access behavioral being stolen.
Oblivious data structures
Oblivious RAM
Goldreich and Ostrovsky proposed this term on software protection.
The memory access of oblivious RAM is probabilistic and the probabilistic distribution is independent of the input. In the paper composed by Goldreich and Ostrovsky have theorem to oblivious RAM: Let RAM(m) denote a RAM with m memory locations and access to a random oracle machine. Then t steps of an arbitrary RAM(m) program can be simulated by less than steps of an oblivious . Every oblivious simulation of RAM(m) must make at least accesses in order to simulate t steps.
Now we have the square-root algorithm to simulate the oblivious ram working.
- For each accesses, randomly permute first memory.
- Check the shelter words first if we want to access a word.
- If the word is there, access one of the dummy words. And if the word is not there, find the permuted location.
To access original RAM in t steps we need to simulate it with steps for the oblivious RAM. For each access, the cost would be O().
Another way to simulate is hierarchical algorithm. The basic idea is to consider the shelter memory as a buffer, and extend it to the multiple levels of buffers. For level I, there are buckets and for each bucket has log t items. For each level there is a random selected hash function.
The operation is like the following: At first load program to the last level, which can be say has buckets. For reading, check the bucket from each level, If (V,X) is already found, pick a bucket randomly to access, and if it is not found, check the bucket , there is only one real match and remaining are dummy entries . For writing, put (V,X) to the first level, and if the first I levels are full, move all I levels to levels and empty the first I levels.
The time cost for each level cost O(log t); cost for every access is ; The cost of Hashing is .
Oblivious tree
An Oblivious Tree is a rooted tree with the following property:
- All the leaves are in the same level.
- All the internal nodes have degree at most 3.
- Only the nodes along the rightmost path in the tree may have degree of one.
The oblivious tree is a data structure similar to 2–3 tree, but with the additional property of being oblivious. The rightmost path may have degree one and this can help to describe the update algorithms. Oblivious tree requires randomization to achieve a running time for the update operations. And for two sequences of operations M and N acting to the tree, the output of the tree has the same output probability distributions. For the tree, there are three operations:
CREATE (L)- build a new tree storing the sequence of values L at its leaves.
INSERT (b, i,T)- insert a new leaf node storing the value b as the i leaf of the tree T.
DELETE (i, T)- remove the i leaf from T.
Step of Create: The list of nodes at the ilevel is obtained traversing the list of nodes at level i+1 from left to right and repeatedly doing the following:
- Choose d {2, 3} uniformly at random.
- If there are less than d nodes left at level i+1, set d equal to the number of nodes left.
- Create a new node n at level I with the next d nodes at level i+1 as children and compute the size of n as the sum of the sizes of its children.
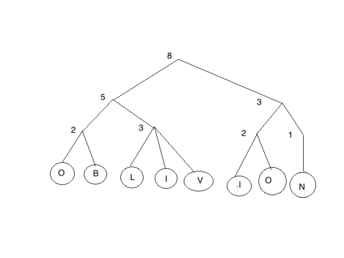
oblivious tree
For example, if the coin tosses of d {2, 3} has an outcome of: 2, 3, 2, 2, 2, 2, 3 stores the string “OBLIVION” as follow oblivious tree.
Both the INSERT (b, I, T) and DELETE(I, T) have the O(log n) expected running time. And for INSERT and DELETE
we have:
INSERT (b, I, CREATE (L)) = CREATE (L + …….., L, b, L………..) DELETE (I, CREATE (L)) = CREATE (L+ ………L, L, ………..)
For example, if the CREATE (ABCDEFG) or INSERT (C, 2, CREATE (ABDEFG)) is run, it yields the same probabilities of out come between these two operations.
References
- Wang, Xiao; Nayak, Kartik; Liu, Chang; Chan, Hubert; Shi, Elaine; Stefanov, Emil; Huang, Yan (November 2014). "Oblivious Data Structures". CCS '14: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security. Scottsdale, Arizona. pp. 215–226. doi:10.1145/2660267.2660314.
- Micciancio, Daniele (May 1997). "Oblivious data structures: applications to cryptography". STOC '97: Proceedings of the twenty-ninth annual ACM symposium on Theory of computing. Symposium on Theory of Computing. El Paso, Texas. pp. 456–464. doi:10.1145/258533.258638.
- Goldreich, Oded; Ostrovsky, Rafail (May 1996). "Software protection and simulation on oblivious RAMs". Journal of the ACM. 43 (3). Association for Computing Machinery: 431–473. doi:10.1145/233551.233553.
- Mitchell, John C.; Zimmerman, Joe (March 2014). "Data-Oblivious Data Structures". 31st International Symposium on Theoretical Aspects of Computer Science. Symposium on Theoretical Aspects of Computer Science. Lyon, France. pp. 554–565. doi:10.4230/LIPIcs.STACS.2014.554.
- Gentry, Craig; Goldman, Kenny A.; Halevi, Shai; Jutla, Charanjit S.; Raykova, Mariana; Wichs, Daniel (July 2013). "Optimizing ORAM and Using It Efficiently for Secure Computation". 13th International Symposium, PETS 2013. Privacy Enhancing Technologies Symposium. Bloomington, IN. doi:10.1007/978-3-642-39077-7_1.
 steps of an oblivious
steps of an oblivious  . Every oblivious simulation of RAM(m) must make at least
. Every oblivious simulation of RAM(m) must make at least  accesses in order to simulate t steps.
accesses in order to simulate t steps.
 accesses, randomly permute first
accesses, randomly permute first  memory.
memory. steps for the oblivious RAM. For each access, the cost would be O(
steps for the oblivious RAM. For each access, the cost would be O( ).
).
 buckets and for each bucket has log t items. For each level there is a random selected hash function.
buckets and for each bucket has log t items. For each level there is a random selected hash function.
 buckets. For reading, check the bucket
buckets. For reading, check the bucket  from each level, If (V,X) is already found, pick a bucket randomly to access, and if it is not found, check the bucket
from each level, If (V,X) is already found, pick a bucket randomly to access, and if it is not found, check the bucket  levels and empty the first I levels.
levels and empty the first I levels.
 ; The cost of Hashing is
; The cost of Hashing is  .
.
 running time for the update operations. And for two sequences of operations M and N acting to the tree, the output of the tree has the same output probability distributions. For the tree, there are three operations:
running time for the update operations. And for two sequences of operations M and N acting to the tree, the output of the tree has the same output probability distributions. For the tree, there are three operations: