
Open channel spillways are dam spillways that utilize the principles of open-channel flow to convey impounded water in order to prevent dam failure. They can function as principal spillways, emergency spillways, or both. They can be located on the dam itself or on a natural grade in the vicinity of the dam.
Spillway types

Chute spillway
Chute spillways carry supercritical flow through the steep slope of an open channel. There are four main components of a chute spillway: The elements of a spillway are the inlet, the vertical curve section (ogee curve), the steep-sloped channel and the outlet.
In order to avoid a hydraulic jump, the slope of the spillway must be steep enough for the flow to remain supercritical.
Proper spillways help with flood control, prevent erosion at the ends of terraces, outlets, and waterways, reduce runoff over drainage ditch banks and are simple to construct.
However, they can only be constructed at sites with natural drainage and moderate temperature variation and have a shorter life expectancy than other spillways.
Stepped spillways
Stepped spillways are used to dissipate energy along the chute of the channel. The steps of the spillway greatly reduce the kinetic energy of the flow and therefore reduce flow velocity. Roller-compacted concrete (RCC) stepped spillways have become increasingly popular because of their use in rehabilitating aged flood control dams.
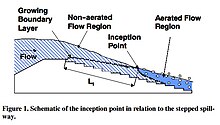
Design guidelines for these spillways are limited. However, research attempts to assist engineers. The two main design components are the inception point (where flow bulking first occurs—increased flow depth) and the energy dissipation that occurs.
Stepped spillways are useful for flood control, increasing dissolved oxygen (DO) levels downstream of a dam, aid wastewater treatment plants for air-water transfer of gases and for volatile organic compound (VOC) removal and reduces the spillway length or eliminates need for stilling basin.
However, few design guidelines are in place and stepped spillways have only been successful for small unit discharges where step height can influence the flow.
Side channel spillways
Side channel spillways are typically used to discharge floods perpendicular to the general direction of flow by placing the control weir parallel to the upper portion of the discharge channel.
It offers low flow velocities upstream and minimizes erosion.
However, it can cause a sudden increase in reservoir level if the channel is submerged.
Flow rates
Different agencies have different methods and formulas for quantifying flows and conveyance capacities for chute spillways. The Natural Resources Conservation Service (NRCS) produced handbooks on dam design. In the National Engineering Handbook, Section 14, Chute Spillways (NEH14), flow equations are given for straight inlets and box inlets.
NEH14 provides the following discharge-head relationship for straight inlets of chute spillways, which is given by the flow equation for a weir:
Q = 3.1W = 3.1Hewhere:
- Q = discharge of inlet (ft/s)
- W = width of the chute or inlet (ft)
- H = depth of flow over the crest (or floor) of the inlet (ft)
- He = specific energy head in reference to the crest of the inlet, or the head over the crest of the inlet (ft)
- va = mean velocity of approach at which the depth H is measured (ft/s)
- g = 32.16 ft/s
Straight inlet

If the flow rate per unit width is defined as q = Q/W, then the equation can be written as:
q = Q/W = 3.1 = 3.1HeThe coefficient, 3.1 varies for different entrance conditions. The value of the coefficient is slightly higher if the conveyance channel has a greater width than the inlet. The value 3.1 is based on the assumption that He and va are measured at a location that exhibits subcritical flow conditions.
NEH14 also provides the following relationship for side channel inlets:
Qmi = 3.1Lhwhere:
- Qmi = discharge capacity without freeboard (ft/s)
(In this case, freeboard is the vertical distance from the water surface to the dam crest when the water surface is at a lower elevation.) - L = length of the spillway crest (ft)
- H = height of the sidewalls above the spillway crest (ft)
Side channel inlet

The United States Bureau of Reclamation (USBR) also uses the weir formula to quantify flow over a chute spillway. The USBR flow equation is:
Q = CLHwhere:
- Q = flow (ft/s)
- L = spillway crest length (or width) (ft)
- H = elevation difference between the reservoir water surface and the spillway crest
- C = discharge coefficient, which varies as follows:
| For H = 1 ft | C = 3.2 |
| 2 | 3.4 |
| 3 | 3.6 |
| 4 | 3.7 |
| 5 | 3.8 |
Example: For a spillway crest length/width of 25 ft, Q will vary with H as follows:

For the NRCS computations, the mean velocity of approach was assumed to be zero. For the USBR computations, it was assumed that linear interpolation could be used to obtain C from H. For a given depth at the spillway crest, the flows calculated using the USBR method are higher than those from the NRCS method because of the higher discharge coefficients. C increases with H under the USBR method, whereas C is assumed to be constant with respect to H under the NRCS method.
Flow regimes
Chute spillways
The flow coming into the spillway is subcritical. The slope of the chute causes the flow velocity to increase. Typically, supercritical flow is maintained in the chute.
Stepped spillway
The flow over a stepped spillway is classified as either nappe flow or skimming flow. Nappe flow regimes occur for small discharges and flat slopes. If the discharge is increased or the slope of the channel is increased, a skimming flow regime can occur (Shahheydari et al. 2015). Nappe flow has pockets of air at each step whereas skimming flow does not. The onset of skimming flow can be defined as:
(dc)=1.057*h - 0.465*h/l
Where:
- h = step height (m)
- l = step length (m)
- (dc)onset = the critical depth of the onset of skimming flow (m)

Nappe flow
For the nappe flow regime, a partially or fully developed hydraulic jump occurs as a result of the jets created between each step.
Ungated spillway:
Gated spillway:
Where:
- Hdam = dam crest head above the downstream toe (m)
- H0 = free surface elevation above the spillway crest (m)
- Hmax = total head (m)
- dc = critical flow depth
- H = head loss (m)
Skimming flow regime
Under a skimming flow regime, water flows in a coherent stream down the step. Water skims the top of each step as it flows down the chute. Recirculating vortices are developed between each step which allow the water to flow over the top of the vortices and skim over each step.
Energy dissipation
Un-gated spillway:
Gated spillway:
where:
- Hdam = dam crest head above the downstream toe (m)
- H0 = free surface elevation above the spillway crest (m)
- Hmax = maximum head available (m)
- dc = critical flow depth (m)
- H = head loss (m)
- f = friction factor
- α = channel slope
Cavitation
Cavitation is the formation of a void, such as a bubble, within a liquid. A fluid passes from a liquid state to a vapor state due to a change in the local pressure while the temperature remains constant. In the case of a dam spillway, this can be caused by turbulence or vortices in flowing water.
Cavitation occurs within the body of flow of a given distributed roughness. However, the exact location where it will occur cannot be predicted. In the case of chute spillways, cavitation occurs at velocities between 12 and 15 m/s.
When cavitation occurs on a spillway, it can cause severe damage. This is especially true when the velocities exceed 25 m/s. Therefore, protection is needed at these velocities. Cavitation can be prevented by decreasing the flow velocity or by increasing the boundary pressure.
Energy dissipation
Every dam needs some form of energy dissipation in its discharge structure to prevent erosion and scour on the downstream side of the dam, since these phenomena can result in dam failure. Plunge pools (also called stilling basins) and impact boxes are two examples of energy dissipators used on dams.
Many USBR dams use energy dissipating blocks for chute spillways (also called baffled aprons). These blocks help induce a hydraulic jump to establish subcritical flow conditions on the downstream side of the dam.
The steps on stepped spillways can be used for energy dissipation. However, they tend to be effective only at dissipating energy at low flows (i.e. skimming flow).
See also
References
- Beauchamp, K.H. "Structures". Engineering Field Manual. United States Department of Agriculture – Soil Conservation Service.
- ^ Hunt, S.L.; Kadavy, K.C. (2010). "Energy Dissipation on Flat-Sloped Stepped Spillways: Part 2. Downstream of the Inception Point". American Society of Agricultural and Biological Engineers. pp. 111–118. ISSN 2151-0032.
- ^ Frizell, K.H. "Hydraulics of Stepped Spillways for RCC Dams and Dam Rehabilitations. PAP-596" (PDF). United States Department of the Interior – Bureau of Reclamation.
- Hager, W.H.; Phister, M. (2011). "Historical Development of Side-Channel Spillway in Hydraulic Engineering" (PDF). Brisbane, Australia.
- ^ United States Department of Agriculture – Soil Conservation Service (1985). Engineering Handbook, Section 14, Chute Spillways (NEH14).
- Blair, H. K.; Rhone, T. J. (1987). "Design of Small Dams" (PDF) (3rd ed.). United States Department of the Interior – Bureau of Reclamation. Archived from the original (PDF) on 2014-02-22.
- ^ Chanson, Hubert (1994). "Comparison of energy dissipation between nappe and skimming flow regimes on stepped chutes" (PDF). Journal of Hydraulic Research. 32 (2): 213–218. doi:10.1080/00221686.1994.10750036.
- Chatila, Jean G.; Jurdi, Bassam R. (2004). "Stepped Spillway as an Energy Dissipater". Canadian Water Resources Journal. 29 (3): 147–158. doi:10.4296/cwrj147.
- Chanson, H. Design of Spillway Aeration Devices to prevent Cavitation Damage on Chutes and Spillways. http://staff.civil.uq.edu.au/h.chanson/aer_dev.html
- ^ Kells, J.A. Smith, C.D. (1991). Canadian Journal of Civil Engineering, 1991, 18:358-377, 10.1139/l91-047
- Peterka, A.J. (1984 (Eighth Printing)). Hydraulic Design of Stilling Basins and Energy Dissipators (Engineering Monograph No. 25). United States Department of the Interior – Bureau of Reclamation. http://www.usbr.gov/pmts/hydraulics_lab/pubs/EM/EM25.pdf
11. Shahheydari, H., Nodoshan, E. J., Barati, R., & Moghadam, M. A. (2015). Discharge coefficient and energy dissipation over stepped spillway under skimming flow regime. KSCE Journal of Civil Engineering, 19(4), 1174-1182.
Categories:


