In non-Euclidean geometry, the Poincaré half-plane model is a way of representing the hyperbolic plane using points in the familiar Euclidean plane. Specifically, each point in the hyperbolic plane is represented using a Euclidean point with coordinates whose coordinate is greater than zero, the upper half-plane, and a metric tensor (definition of distance) called the Poincaré metric is adopted, in which the local scale is inversely proportional to the coordinate. Points on the -axis, whose coordinate is equal to zero, represent ideal points (points at infinity), which are outside the hyperbolic plane proper.
Sometimes the points of the half-plane model are considered to lie in the complex plane with positive imaginary part. Using this interpretation, each point in the hyperbolic plane is associated with a complex number.
The half-plane model can be thought of as a map projection from the curved hyperbolic plane to the flat Euclidean plane. From the hyperboloid model (a representation of the hyperbolic plane on a hyperboloid of two sheets embedded in 3-dimensional Minkowski space, analogous to the sphere embedded in 3-dimensional Euclidean space), the half-plane model is obtained by orthographic projection in a direction parallel to a null vector, which can also be thought of as a kind of stereographic projection centered on an ideal point. The projection is conformal, meaning that it preserves angles, and like the stereographic projection of the sphere it projects generalized circles (geodesics, hypercycles, horocycles, and circles) in the hyperbolic plane to generalized circles (lines or circles) in the plane. In particular, geodesics (analogous to straight lines), project to either half-circles whose center has coordinate zero, or to vertical straight lines of constant coordinate, hypercycles project to circles crossing the -axis, horocycles project to either circles tangent to the -axis or to horizontal lines of constant coordinate, and circles project to circles contained entirely in the half-plane.
Hyperbolic motions, the distance-preserving geometric transformations from the hyperbolic plane to itself, are represented in the Poincaré half-plane by the subset of Möbius transformations of the plane which preserve the half-plane; these are conformal, circle-preserving transformations which send the -axis to itself without changing its orientation. When points in the plane are taken to be complex numbers, any Möbius transformation is represented by a linear fractional transformation of complex numbers, and the hyperbolic motions are represented by elements of the projective special linear group .
The Cayley transform provides an isometry between the half-plane model and the Poincaré disk model, which is a stereographic projection of the hyperboloid centered on any ordinary point in the hyperbolic plane, which maps the hyperbolic plane onto a disk in the Euclidean plane, and also shares the properties of conformality and mapping generalized circles to generalized circles.
The Poincaré half-plane model is named after Henri Poincaré, but it originated with Eugenio Beltrami who used it, along with the Klein model and the Poincaré disk model, to show that hyperbolic geometry was equiconsistent with Euclidean geometry.
The half-plane model can be generalized to the Poincaré half-space model of -dimensional hyperbolic space by replacing the single coordinate by distinct coordinates.
Metric
The metric of the model on the half-plane, is:
where s measures the length along a (possibly curved) line. The straight lines in the hyperbolic plane (geodesics for this metric tensor, i.e., curves which minimize the distance) are represented in this model by circular arcs perpendicular to the x-axis (half-circles whose centers are on the x-axis) and straight vertical rays perpendicular to the x-axis.
Distance calculation



If and are two points in the half-plane and is the reflection of across the x-axis into the lower half plane, the distance between the two points under the hyperbolic-plane metric is:
where is the Euclidean distance between points and , is the inverse hyperbolic sine, and is the inverse hyperbolic tangent. This formula can be thought of as coming from the chord length in the Minkowski metric between points in the hyperboloid model, , analogous to finding arclength on a sphere in terms of chord length. This formula can be thought of as coming from Euclidean distance in the Poincaré disk model with one point at the origin, analogous to finding arclength on the sphere by taking a stereographic projection centered on one point and measuring the Euclidean distance in the plane from the origin to the other point.
If the two points and are on a hyperbolic line (Euclidean half-circle) which intersects the x-axis at the ideal points and the distance from to is:
Cf. Cross-ratio.
Some special cases can be simplified. Two points with the same coordinate:
Two points with the same coordinate:
One point at the apex of the semicircle and another point at a central angle of .
where is the inverse Gudermannian function.
Special points and curves
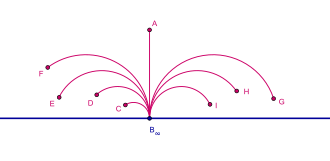
Ideal points (points at infinity) in the Poincaré half-plane model are of two kinds: the points on the -axis, and one imaginary point at which is the ideal point to which all lines orthogonal to the -axis converge.
Straight lines, geodesics (the shortest path between the points contained within it) are modeled by either half-circles whose origin is on the x-axis, or straight vertical rays orthogonal to the x-axis.
A circle (curve equidistant from a central point) with center and radius is modeled by a circle with center and radius .
A hypercycle (a curve equidistant from a straight line, its axis) is modeled by either a circular arc which intersects the -axis at the same two ideal points as the half-circle which models its axis but at an acute or obtuse angle, or a straight line which intersects the -axis at the same point as the vertical line which models its axis, but at an acute or obtuse angle.
A horocycle (a curve whose normals all converge asymptotically in the same direction, its center) is modeled by either a circle tangent to the -axis (but excluding the ideal point of intersection, which is its center), or a line parallel to the -axis, in which case the center is the ideal point at .
Euclidean synopsis
A Euclidean circle with center and radius represents:
- when the circle is completely inside the halfplane a hyperbolic circle with center and radius
- when the circle is completely inside the halfplane and touches the boundary a horocycle centered around the ideal point
- when the circle intersects the boundary orthogonal a hyperbolic line
- when the circle intersects the boundary non- orthogonal a hypercycle.
Compass and straightedge constructions
See also: Compass and straightedge constructionsHere is how one can use compass and straightedge constructions in the model to achieve the effect of the basic constructions in the hyperbolic plane. For example, how to construct the half-circle in the Euclidean half-plane which models a line on the hyperbolic plane through two given points.
Creating the line through two existing points
Draw the line segment between the two points. Construct the perpendicular bisector of the line segment. Find its intersection with the x-axis. Draw the circle around the intersection which passes through the given points. Erase the part which is on or below the x-axis.
Or in the special case where the two given points lie on a vertical line, draw that vertical line through the two points and erase the part which is on or below the x-axis.
Creating the circle through one point with center another point
If the two points are not on a vertical line: Draw the radial line (half-circle) between the two given points as in the previous case. Construct a tangent to that line at the non-central point. Drop a perpendicular from the given center point to the x-axis. Find the intersection of these two lines to get the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.
If the two given points lie on a vertical line and the given center is above the other given point: Draw a circle around the intersection of the vertical line and the x-axis which passes through the given central point. Draw a horizontal line through the non-central point. Construct the tangent to the circle at its intersection with that horizontal line. The midpoint between the intersection of the tangent with the vertical line and the given non-central point is the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.
If the two given points lie on a vertical line and the given center is below the other given point: Draw a circle around the intersection of the vertical line and the x-axis which passes through the given central point. Draw a line tangent to the circle which passes through the given non-central point. Draw a horizontal line through that point of tangency and find its intersection with the vertical line. The midpoint between that intersection and the given non-central point is the center of the model circle. Draw the model circle around that new center and passing through the given non-central point.
Given a circle find its (hyperbolic) center
Drop a perpendicular p from the Euclidean center of the circle to the x-axis. Let point q be the intersection of this line and the x- axis. Draw a line tangent to the circle going through q. Draw the half circle h with center q going through the point where the tangent and the circle meet. The (hyperbolic) center is the point where h and p intersect.
Other constructions
Creating the point which is the intersection of two existing lines, if they intersect: Find the intersection of the two given semicircles (or vertical lines).
Creating the one or two points in the intersection of a line and a circle (if they intersect): Find the intersection of the given semicircle (or vertical line) with the given circle.
Creating the one or two points in the intersection of two circles (if they intersect): Find the intersection of the two given circles.
Symmetry groups

The projective linear group PGL(2,C) acts on the Riemann sphere by the Möbius transformations. The subgroup that maps the upper half-plane, H, onto itself is PSL(2,R), the transforms with real coefficients, and these act transitively and isometrically on the upper half-plane, making it a homogeneous space.
There are four closely related Lie groups that act on the upper half-plane by fractional linear transformations and preserve the hyperbolic distance.
- The special linear group SL(2,R) which consists of the set of 2×2 matrices with real entries whose determinant equals +1. Note that many texts (including Misplaced Pages) often say SL(2,R) when they really mean PSL(2,R).
- The group S*L(2,R) consisting of the set of 2×2 matrices with real entries whose determinant equals +1 or −1. Note that SL(2,R) is a subgroup of this group.
- The projective special linear group PSL(2,R) = SL(2,R)/{±I}, consisting of the matrices in SL(2,R) modulo plus or minus the identity matrix.
- The group PSL(2,R) = SL(2,R)/{±I}=PGL(2,R) is again a projective group, and again, modulo plus or minus the identity matrix. PSL(2,R) is contained as an index-two normal subgroup, the other coset being the set of 2×2 matrices with real entries whose determinant equals −1, modulo plus or minus the identity.
The relationship of these groups to the Poincaré model is as follows:
- The group of all isometries of H, sometimes denoted as Isom(H), is isomorphic to PSL(2,R). This includes both the orientation preserving and the orientation-reversing isometries. The orientation-reversing map (the mirror map) is .
- The group of orientation-preserving isometries of H, sometimes denoted as Isom(H), is isomorphic to PSL(2,R).
Important subgroups of the isometry group are the Fuchsian groups.
One also frequently sees the modular group SL(2,Z). This group is important in two ways. First, it is a symmetry group of the square 2x2 lattice of points. Thus, functions that are periodic on a square grid, such as modular forms and elliptic functions, will thus inherit an SL(2,Z) symmetry from the grid. Second, SL(2,Z) is of course a subgroup of SL(2,R), and thus has a hyperbolic behavior embedded in it. In particular, SL(2,Z) can be used to tessellate the hyperbolic plane into cells of equal (Poincaré) area.
Isometric symmetry
The group action of the projective special linear group on is defined by
Note that the action is transitive: for any , there exists a such that . It is also faithful, in that if for all then g = e.
The stabilizer or isotropy subgroup of an element is the set of which leave z unchanged: gz = z. The stabilizer of i is the rotation group
Since any element is mapped to i by some element of , this means that the isotropy subgroup of any z is isomorphic to SO(2). Thus, . Alternatively, the bundle of unit-length tangent vectors on the upper half-plane, called the unit tangent bundle, is isomorphic to .
The upper half-plane is tessellated into free regular sets by the modular group
Geodesics
Main article: Anosov flowThe geodesics for this metric tensor are circular arcs perpendicular to the real axis (half-circles whose origin is on the real axis) and straight vertical lines ending on the real axis.
The unit-speed geodesic going up vertically, through the point i is given by
Because PSL(2,R) acts transitively by isometries of the upper half-plane, this geodesic is mapped into the other geodesics through the action of PSL(2,R). Thus, the general unit-speed geodesic is given by
This provides a basic description of the geodesic flow on the unit-length tangent bundle (complex line bundle) on the upper half-plane. Starting with this model, one can obtain the flow on arbitrary Riemann surfaces, as described in the article on the Anosov flow.
The model in three dimensions
The metric of the model on the half- space is given by
where s measures length along a possibly curved line. The straight lines in the hyperbolic space (geodesics for this metric tensor, i.e. curves which minimize the distance) are represented in this model by circular arcs normal to the z = 0-plane (half-circles whose origin is on the z = 0-plane) and straight vertical rays normal to the z = 0-plane.
The distance between two points and measured in this metric along such a geodesic is:
The model in n dimensions
This model can be generalized to model an dimensional hyperbolic space by replacing the real number x by a vector in an n dimensional Euclidean vector space.
See also
- Angle of parallelism
- Anosov flow
- Fuchsian group
- Fuchsian model
- Hyperbolic motion
- Kleinian model
- Models of the hyperbolic plane
- Pseudosphere
- Schwarz–Ahlfors–Pick theorem
- Ultraparallel theorem
References
- Notes
- "Distance formula for points in the Poincare half plane model on a "vertical geodesic"". mathematics stackexchange. August 6, 2015. Retrieved 19 September 2015.
- Bochaca, Judit Abardia. "Tools to work with the Half-Plane model". Tools to work with the Half-Plane mode. Retrieved 25 June 2015.
- Flavors of Geometry, MSRI Publications, Volume 31, 1997, Hyperbolic Geometry, J. W. Cannon, W. J. Floyd, R. Kenyon and W. R. Parry, page 87, Figure 19. Constructing the hyperbolic center of a circle
- Sources
- Eugenio Beltrami, Teoria fondamentale degli spazi di curvatura constante, Annali di Matematica Pura ed Applicata, ser II 2 (1868), 232–255
- Henri Poincaré (1882) "Théorie des Groupes Fuchsiens", Acta Mathematica v.1, p. 1. First article in a series exploiting the half-plane model. An archived copy is freely available. On page 52 one can see an example of the semicircle diagrams so characteristic of the model.
- Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. ISBN 0-387-90465-4.
- Jürgen Jost, Compact Riemann Surfaces (2002), Springer-Verlag, New York. ISBN 3-540-43299-X (See Section 2.3).
- Saul Stahl, The Poincaré Half-Plane, Jones and Bartlett, 1993, ISBN 0-86720-298-X.
- John Stillwell (1998) Numbers and Geometry, pp. 100–104, Springer-Verlag, NY ISBN 0-387-98289-2. An elementary introduction to the Poincaré half-plane model of the hyperbolic plane.
 whose
whose  coordinate is greater than zero, the
coordinate is greater than zero, the  -axis, whose
-axis, whose  .
.
 -dimensional
-dimensional  distinct coordinates.
distinct coordinates.
 is:
is:

 and
and  are two points in the half-plane
are two points in the half-plane  and
and  is the reflection of
is the reflection of  across the x-axis into the lower half plane, the distance between the two points under the hyperbolic-plane metric is:
across the x-axis into the lower half plane, the distance between the two points under the hyperbolic-plane metric is:

 is the
is the  and
and  ,
, 
 is the
is the 
 is the
is the  formula can be thought of as coming from the
formula can be thought of as coming from the 
 , analogous to finding arclength on a sphere in terms of chord length. This
, analogous to finding arclength on a sphere in terms of chord length. This  formula can be thought of as coming from Euclidean distance in the
formula can be thought of as coming from Euclidean distance in the  are on a hyperbolic line (Euclidean half-circle) which intersects the x-axis at the ideal points
are on a hyperbolic line (Euclidean half-circle) which intersects the x-axis at the ideal points  and
and  the distance from
the distance from 

 coordinate:
coordinate:

 at the
at the  and another point at a central angle of
and another point at a central angle of  .
.

 is the inverse
is the inverse  which is the
which is the  is modeled by a circle with center
is modeled by a circle with center  and radius
and radius  .
.
 and radius
and radius  represents:
represents:
 and radius
and radius 

 a hyperbolic line
a hyperbolic line .
. on
on  is defined by
is defined by

 , there exists a
, there exists a  such that
such that  . It is also faithful, in that if
. It is also faithful, in that if  for all
for all  then g = e.
then g = e.
 is the set of
is the set of 
 . Alternatively, the
. Alternatively, the 


 is given by
is given by

 and
and  measured in this metric along such a geodesic is:
measured in this metric along such a geodesic is:

 dimensional
dimensional