In physics, a quantum phase transition (QPT) is a phase transition between different quantum phases (phases of matter at zero temperature). Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter—such as magnetic field or pressure—at absolute zero temperature. The transition describes an abrupt change in the ground state of a many-body system due to its quantum fluctuations. Such a quantum phase transition can be a second-order phase transition. Quantum phase transitions can also be represented by the topological fermion condensation quantum phase transition, see e.g. strongly correlated quantum spin liquid. In case of three dimensional Fermi liquid, this transition transforms the Fermi surface into a Fermi volume. Such a transition can be a first-order phase transition, for it transforms two dimensional structure (Fermi surface) into three dimensional. As a result, the topological charge of Fermi liquid changes abruptly, since it takes only one of a discrete set of values.
Classical description
To understand quantum phase transitions, it is useful to contrast them to classical phase transitions (CPT) (also called thermal phase transitions). A CPT describes a cusp in the thermodynamic properties of a system. It signals a reorganization of the particles; A typical example is the freezing transition of water describing the transition between liquid and solid. The classical phase transitions are driven by a competition between the energy of a system and the entropy of its thermal fluctuations. A classical system does not have entropy at zero temperature and therefore no phase transition can occur. Their order is determined by the first discontinuous derivative of a thermodynamic potential.
A phase transition from water to ice, for example, involves latent heat (a discontinuity of the internal energy ) and is of first order. A phase transition from a ferromagnet to a paramagnet is continuous and is of second order. (See phase transition for Ehrenfest's classification of phase transitions by the derivative of free energy which is discontinuous at the transition). These continuous transitions from an ordered to a disordered phase are described by an order parameter, which is zero in the disordered and nonzero in the ordered phase. For the aforementioned ferromagnetic transition, the order parameter would represent the total magnetization of the system.
Although the thermodynamic average of the order parameter is zero in the disordered state, its fluctuations can be nonzero and become long-ranged in the vicinity of the critical point, where their typical length scale ξ (correlation length) and typical fluctuation decay time scale τc (correlation time) diverge:
where
is defined as the relative deviation from the critical temperature Tc. We call ν the (correlation length) critical exponent and z the dynamical critical exponent. Critical behavior of nonzero temperature phase transitions is fully described by classical thermodynamics; quantum mechanics does not play any role even if the actual phases require a quantum mechanical description (e.g. superconductivity).
Quantum description
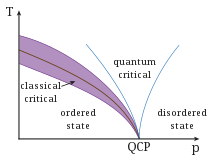
Talking about quantum phase transitions means talking about transitions at T = 0: by tuning a non-temperature parameter like pressure, chemical composition or magnetic field, one could suppress e.g. some transition temperature like the Curie or Néel temperature to 0 K.
As a system in equilibrium at zero temperature is always in its lowest-energy state (or an equally weighted superposition if the lowest-energy is degenerate), a QPT cannot be explained by thermal fluctuations. Instead, quantum fluctuations, arising from Heisenberg's uncertainty principle, drive the loss of order characteristic of a QPT. The QPT occurs at the quantum critical point (QCP), where quantum fluctuations driving the transition diverge and become scale invariant in space and time.
Although absolute zero is not physically realizable, characteristics of the transition can be detected in the system's low-temperature behavior near the critical point. At nonzero temperatures, classical fluctuations with an energy scale of kBT compete with the quantum fluctuations of energy scale ħω. Here ω is the characteristic frequency of the quantum oscillation and is inversely proportional to the correlation time. Quantum fluctuations dominate the system's behavior in the region where ħω > kBT, known as the quantum critical region. This quantum critical behavior manifests itself in unconventional and unexpected physical behavior like novel non Fermi liquid phases. From a theoretical point of view, a phase diagram like the one shown on the right is expected: the QPT separates an ordered from a disordered phase (often, the low temperature disordered phase is referred to as 'quantum' disordered).
At high enough temperatures, the system is disordered and purely classical. Around the classical phase transition, the system is governed by classical thermal fluctuations (light blue area). This region becomes narrower with decreasing energies and converges towards the quantum critical point (QCP). Experimentally, the 'quantum critical' phase, which is still governed by quantum fluctuations, is the most interesting one.
See also
- Superconductor–insulator transition – Type of quantum phase transition
- Quantum phases – Quantum states of matter at zero temperature
- Quantum critical point – Feature of a phase diagram
References
- Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences. 53 (1): 51–81. doi:10.1007/s004070050021. S2CID 121525126.
- Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences. 53 (1): 51–81. doi:10.1007/s004070050021. S2CID 121525126.
- Sachdev, Subir (2011). Quantum Phase Transitions. Cambridge University Press. (2nd ed.). ISBN 978-0-521-51468-2.
- Carr, Lincoln D. (2010). Understanding Quantum Phase Transitions. CRC Press. ISBN 978-1-4398-0251-9.
- Vojta, Thomas (2000). "Quantum phase transitions in electronic systems". Annalen der Physik. 9 (6): 403–440. arXiv:cond-mat/9910514. Bibcode:2000AnP...512..403V. doi:10.1002/1521-3889(200006)9:6<403::AID-ANDP403>3.0.CO;2-R.
- de Souza, Mariano (2020). "Unveiling the Physics of the Mutual Interactions in Paramagnets". Scientific Reports. Vol. 10. doi:10.1038/s41598-020-64632-x.
 ) and is of first order. A phase transition from a
) and is of first order. A phase transition from a 

