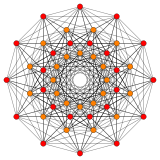
 122 |
 Rectified 122 |
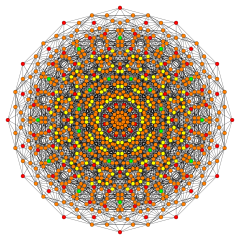 Birectified 122 |
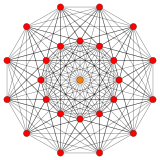 221 |
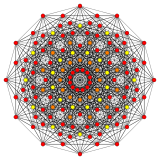 Rectified 221 | |
| orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
In 6-dimensional geometry, the 122 polytope is a uniform polytope, constructed from the E6 group. It was first published in E. L. Elte's 1912 listing of semiregular polytopes, named as V72 (for its 72 vertices).
Its Coxeter symbol is 122, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 1-node sequence. There are two rectifications of the 122, constructed by positions points on the elements of 122. The rectified 122 is constructed by points at the mid-edges of the 122. The birectified 122 is constructed by points at the triangle face centers of the 122.
These polytopes are from a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
122 polytope
| 122 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Family | 1k2 polytope |
| Schläfli symbol | {3,3} |
| Coxeter symbol | 122 |
| Coxeter-Dynkin diagram | |
| 5-faces | 54: 27 121 27 121 |
| 4-faces | 702: 270 111 432 120 |
| Cells | 2160: 1080 110 1080 {3,3} |
| Faces | 2160 {3} |
| Edges | 720 |
| Vertices | 72 |
| Vertex figure | Birectified 5-simplex: 022 
|
| Petrie polygon | Dodecagon |
| Coxeter group | E6, ], order 103680 |
| Properties | convex, isotopic |
The 122 polytope contains 72 vertices, and 54 5-demicubic facets. It has a birectified 5-simplex vertex figure. Its 72 vertices represent the root vectors of the simple Lie group E6.
Alternate names
- Pentacontatetra-peton (Acronym Mo) - 54-facetted polypeton (Jonathan Bowers)
Images
| E6 |
D5 |
D4 / A2 | |
|---|---|---|---|
 (1,2) |
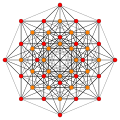 (1,3) |
 (1,9,12) | |
| B6 |
A5 |
A4 ] = |
A3 / D3 |
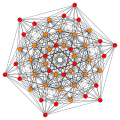 (1,2) |
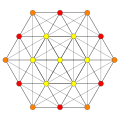 (2,3,6) |
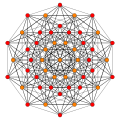 (1,2) |
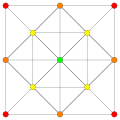 (1,6,8,12) |
Construction
It is created by a Wythoff construction upon a set of 6 hyperplane mirrors in 6-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on either of 2-length branches leaves the 5-demicube, 131, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the birectified 5-simplex, 022, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.
| E6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | notes | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A5 | ( ) | f0 | 72 | 20 | 90 | 60 | 60 | 15 | 15 | 30 | 6 | 6 | r{3,3,3} | E6/A5 = 72*6!/6! = 72 | |
| A2A2A1 | { } | f1 | 2 | 720 | 9 | 9 | 9 | 3 | 3 | 9 | 3 | 3 | {3}×{3} | E6/A2A2A1 = 72*6!/3!/3!/2 = 720 | |
| A2A1A1 | {3} | f2 | 3 | 3 | 2160 | 2 | 2 | 1 | 1 | 4 | 2 | 2 | s{2,4} | E6/A2A1A1 = 72*6!/3!/2/2 = 2160 | |
| A3A1 | {3,3} | f3 | 4 | 6 | 4 | 1080 | * | 1 | 0 | 2 | 2 | 1 | { }∨( ) | E6/A3A1 = 72*6!/4!/2 = 1080 | |
| 4 | 6 | 4 | * | 1080 | 0 | 1 | 2 | 1 | 2 | ||||||
| A4A1 | {3,3,3} | f4 | 5 | 10 | 10 | 5 | 0 | 216 | * | * | 2 | 0 | { } | E6/A4A1 = 72*6!/5!/2 = 216 | |
| 5 | 10 | 10 | 0 | 5 | * | 216 | * | 0 | 2 | ||||||
| D4 | h{4,3,3} | 8 | 24 | 32 | 8 | 8 | * | * | 270 | 1 | 1 | E6/D4 = 72*6!/8/4! = 270 | |||
| D5 | h{4,3,3,3} | f5 | 16 | 80 | 160 | 80 | 40 | 16 | 0 | 10 | 27 | * | ( ) | E6/D5 = 72*6!/16/5! = 27 | |
| 16 | 80 | 160 | 40 | 80 | 0 | 16 | 10 | * | 27 | ||||||
Related complex polyhedron

The regular complex polyhedron 3{3}3{4}2, ![]()
![]()
![]()
![]()
![]() , in has a real representation as the 122 polytope in 4-dimensional space. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces. Its complex reflection group is 332, order 1296. It has a half-symmetry quasiregular construction as
, in has a real representation as the 122 polytope in 4-dimensional space. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces. Its complex reflection group is 332, order 1296. It has a half-symmetry quasiregular construction as ![]()
![]()
![]()
![]()
![]() , as a rectification of the Hessian polyhedron,
, as a rectification of the Hessian polyhedron, ![]()
![]()
![]()
![]()
![]() .
.
Related polytopes and honeycomb
Along with the semiregular polytope, 221, it is also one of a family of 39 convex uniform polytopes in 6-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
| 1k2 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8 | E10 = = E8 | |||
| Coxeter diagram |
|||||||||||
| Symmetry (order) |
] | ||||||||||
| Order | 12 | 120 | 1,920 | 103,680 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph | 
|

|

|

|

|

|
- | - | |||
| Name | 1−1,2 | 102 | 112 | 122 | 132 | 142 | 152 | 162 | |||
Geometric folding
The 122 is related to the 24-cell by a geometric folding E6 → F4 of Coxeter-Dynkin diagrams, E6 corresponding to 122 in 6 dimensions, F4 to the 24-cell in 4 dimensions. This can be seen in the Coxeter plane projections. The 24 vertices of the 24-cell are projected in the same two rings as seen in the 122.
| E6/F4 Coxeter planes | |
|---|---|
 122 |
 24-cell |
| D4/B4 Coxeter planes | |
 122 |
 24-cell |
Tessellations
This polytope is the vertex figure for a uniform tessellation of 6-dimensional space, 222, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Rectified 122 polytope
| Rectified 122 | |
|---|---|
| Type | Uniform 6-polytope |
| Schläfli symbol | 2r{3,3,3} r{3,3} |
| Coxeter symbol | 0221 |
| Coxeter-Dynkin diagram | or |
| 5-faces | 126 |
| 4-faces | 1566 |
| Cells | 6480 |
| Faces | 6480 |
| Edges | 6480 |
| Vertices | 720 |
| Vertex figure | 3-3 duoprism prism |
| Petrie polygon | Dodecagon |
| Coxeter group | E6, ], order 103680 |
| Properties | convex |
The rectified 122 polytope (also called 0221) can tessellate 6-dimensional space as the Voronoi cell of the E6* honeycomb lattice (dual of E6 lattice).
Alternate names
- Birectified 221 polytope
- Rectified pentacontatetrapeton (acronym Ram) - rectified 54-facetted polypeton (Jonathan Bowers)
Images
Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.
| E6 |
D5 |
D4 / A2 |
B6 |
|---|---|---|---|

|

|
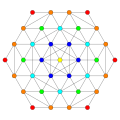
|
|
| A5 |
A4 |
A3 / D3 | |
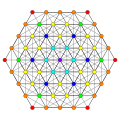
|

|
|
Construction
Its construction is based on the E6 group and information can be extracted from the ringed Coxeter-Dynkin diagram representing this polytope: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the ring on the short branch leaves the birectified 5-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the ring on the either 2-length branch leaves the birectified 5-orthoplex in its alternated form: t2(211), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The vertex figure is determined by removing the ringed node and ringing the neighboring ring. This makes 3-3 duoprism prism, {3}×{3}×{}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.
| E6 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | k-figure | notes | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A2A2A1 | ( ) | f0 | 720 | 18 | 18 | 18 | 9 | 6 | 18 | 9 | 6 | 9 | 6 | 3 | 6 | 9 | 3 | 2 | 3 | 3 | {3}×{3}×{ } | E6/A2A2A1 = 72*6!/3!/3!/2 = 720 | |
| A1A1A1 | { } | f1 | 2 | 6480 | 2 | 2 | 1 | 1 | 4 | 2 | 1 | 2 | 2 | 1 | 2 | 4 | 1 | 1 | 2 | 2 | { }∨{ }∨( ) | E6/A1A1A1 = 72*6!/2/2/2 = 6480 | |
| A2A1 | {3} | f2 | 3 | 3 | 4320 | * | * | 1 | 2 | 1 | 0 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 2 | 1 | Sphenoid | E6/A2A1 = 72*6!/3!/2 = 4320 | |
| 3 | 3 | * | 4320 | * | 0 | 2 | 0 | 1 | 1 | 1 | 0 | 2 | 2 | 1 | 1 | 1 | 2 | ||||||
| A2A1A1 | 3 | 3 | * | * | 2160 | 0 | 0 | 2 | 0 | 2 | 0 | 1 | 0 | 4 | 1 | 0 | 2 | 2 | { }∨{ } | E6/A2A1A1 = 72*6!/3!/2/2 = 2160 | |||
| A2A1 | {3,3} | f3 | 4 | 6 | 4 | 0 | 0 | 1080 | * | * | * | * | 2 | 1 | 0 | 0 | 0 | 1 | 2 | 0 | { }∨( ) | E6/A2A1 = 72*6!/3!/2 = 1080 | |
| A3 | r{3,3} | 6 | 12 | 4 | 4 | 0 | * | 2160 | * | * | * | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | {3} | E6/A3 = 72*6!/4! = 2160 | ||
| A3A1 | 6 | 12 | 4 | 0 | 4 | * | * | 1080 | * | * | 0 | 1 | 0 | 2 | 0 | 0 | 2 | 1 | { }∨( ) | E6/A3A1 = 72*6!/4!/2 = 1080 | |||
| {3,3} | 4 | 6 | 0 | 4 | 0 | * | * | * | 1080 | * | 0 | 0 | 2 | 0 | 1 | 1 | 0 | 2 | |||||
| r{3,3} | 6 | 12 | 0 | 4 | 4 | * | * | * | * | 1080 | 0 | 0 | 0 | 2 | 1 | 0 | 1 | 2 | |||||
| A4 | r{3,3,3} | f4 | 10 | 30 | 20 | 10 | 0 | 5 | 5 | 0 | 0 | 0 | 432 | * | * | * | * | 1 | 1 | 0 | { } | E6/A4 = 72*6!/5! = 432 | |
| A4A1 | 10 | 30 | 20 | 0 | 10 | 5 | 0 | 5 | 0 | 0 | * | 216 | * | * | * | 0 | 2 | 0 | E6/A4A1 = 72*6!/5!/2 = 216 | ||||
| A4 | 10 | 30 | 10 | 20 | 0 | 0 | 5 | 0 | 5 | 0 | * | * | 432 | * | * | 1 | 0 | 1 | E6/A4 = 72*6!/5! = 432 | ||||
| D4 | {3,4,3} | 24 | 96 | 32 | 32 | 32 | 0 | 8 | 8 | 0 | 8 | * | * | * | 270 | * | 0 | 1 | 1 | E6/D4 = 72*6!/8/4! = 270 | |||
| A4A1 | r{3,3,3} | 10 | 30 | 0 | 20 | 10 | 0 | 0 | 0 | 5 | 5 | * | * | * | * | 216 | 0 | 0 | 2 | E6/A4A1 = 72*6!/5!/2 = 216 | |||
| A5 | 2r{3,3,3,3} | f5 | 20 | 90 | 60 | 60 | 0 | 15 | 30 | 0 | 15 | 0 | 6 | 0 | 6 | 0 | 0 | 72 | * | * | ( ) | E6/A5 = 72*6!/6! = 72 | |
| D5 | 2r{4,3,3,3} | 80 | 480 | 320 | 160 | 160 | 80 | 80 | 80 | 0 | 40 | 16 | 16 | 0 | 10 | 0 | * | 27 | * | E6/D5 = 72*6!/16/5! = 27 | |||
| 80 | 480 | 160 | 320 | 160 | 0 | 80 | 40 | 80 | 80 | 0 | 0 | 16 | 10 | 16 | * | * | 27 | ||||||
Truncated 122 polytope
| Truncated 122 | |
|---|---|
| Type | Uniform 6-polytope |
| Schläfli symbol | t{3,3} |
| Coxeter symbol | t(122) |
| Coxeter-Dynkin diagram | or |
| 5-faces | 72+27+27 |
| 4-faces | 32+216+432+270+216 |
| Cells | 1080+2160+1080+1080+1080 |
| Faces | 4320+4320+2160 |
| Edges | 6480+720 |
| Vertices | 1440 |
| Vertex figure | ( )v{3}x{3} |
| Petrie polygon | Dodecagon |
| Coxeter group | E6, ], order 103680 |
| Properties | convex |
Alternate names
- Truncated 122 polytope
Construction
Its construction is based on the E6 group and information can be extracted from the ringed Coxeter-Dynkin diagram representing this polytope: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.
| E6 |
D5 |
D4 / A2 |
B6 |
|---|---|---|---|
|

|
|

|
| A5 |
A4 |
A3 / D3 | |

|

|

|
Birectified 122 polytope
| Birectified 122 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Schläfli symbol | 2r{3,3} |
| Coxeter symbol | 2r(122) |
| Coxeter-Dynkin diagram | or |
| 5-faces | 126 |
| 4-faces | 2286 |
| Cells | 10800 |
| Faces | 19440 |
| Edges | 12960 |
| Vertices | 2160 |
| Vertex figure | |
| Coxeter group | E6, ], order 103680 |
| Properties | convex |
Alternate names
- Bicantellated 221
- Birectified pentacontitetrapeton (barm) (Jonathan Bowers)
Images
Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.
| E6 |
D5 |
D4 / A2 |
B6 |
|---|---|---|---|
|

|
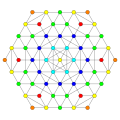
|
|
| A5 |
A4 |
A3 / D3 | |

|
|
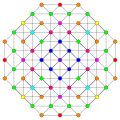
|
Trirectified 122 polytope
| Trirectified 122 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Schläfli symbol | 3r{3,3} |
| Coxeter symbol | 3r(122) |
| Coxeter-Dynkin diagram | or |
| 5-faces | 558 |
| 4-faces | 4608 |
| Cells | 8640 |
| Faces | 6480 |
| Edges | 2160 |
| Vertices | 270 |
| Vertex figure | |
| Coxeter group | E6, ], order 103680 |
| Properties | convex |
Alternate names
- Tricantellated 221
- Trirectified pentacontitetrapeton (trim or cacam) (Jonathan Bowers)
See also
Notes
- Elte, 1912
- Klitzing, (o3o3o3o3o *c3x - mo)
- ^ Coxeter, Regular Polytopes, 11.8 Gossett figures in six, seven, and eight dimensions, p. 202-203
- Coxeter, H. S. M., Regular Complex Polytopes, second edition, Cambridge University Press, (1991). p.30 and p.47
- The Voronoi Cells of the E6* and E7* Lattices Archived 2016-01-30 at the Wayback Machine, Edward Pervin
- Klitzing, (o3o3x3o3o *c3o - ram)
- Klitzing, Richard. "6D convex uniform polypeta o3o3x3o3o *c3o - ram".
- Klitzing, (o3x3o3x3o *c3o - barm)
- Klitzing, (x3o3o3o3x *c3o - cacam
References
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, See p334 (figure 3.6a) by Peter mcMullen: (12-gonal node-edge graph of 122)
- Klitzing, Richard. "6D uniform polytopes (polypeta)". o3o3o3o3o *c3x - mo, o3o3x3o3o *c3o - ram, o3x3o3x3o *c3o - barm
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 has a real representation as the 122 polytope in 4-dimensional space. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces. Its
has a real representation as the 122 polytope in 4-dimensional space. It has 72 vertices, 216 3-edges, and 54 3{3}3 faces. Its  = E8
= E8
 = E8
= E8