| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2022) (Learn how and when to remove this message) |
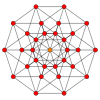 5-cube |
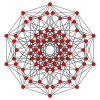 Rectified 5-cube |
 Birectified 5-cube Birectified 5-orthoplex | ||
 5-orthoplex |
 Rectified 5-orthoplex | |||
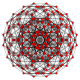
| Orthogonal projections in A5 Coxeter plane | ||||
|---|---|---|---|---|
In five-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.
There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the 5-orthoplex. Vertices of the rectified 5-cube are located at the edge-centers of the 5-cube. Vertices of the birectified 5-cube are located in the square face centers of the 5-cube.
Rectified 5-cube
| Rectified 5-cube rectified penteract (rin) | ||
|---|---|---|
| Type | uniform 5-polytope | |
| Schläfli symbol | r{4,3,3,3} | |
| Coxeter diagram | ||
| 4-faces | 42 | 10 32 |
| Cells | 200 | 40 160 |
| Faces | 400 | 80 320 |
| Edges | 320 | |
| Vertices | 80 | |
| Vertex figure |  Tetrahedral prism | |
| Coxeter group | B5, , order 3840 | |
| Dual | ||
| Base point | (0,1,1,1,1,1)√2 | |
| Circumradius | sqrt(2) = 1.414214 | |
| Properties | convex, isogonal | |
Alternate names
- Rectified penteract (acronym: rin) (Jonathan Bowers)
Construction
The rectified 5-cube may be constructed from the 5-cube by truncating its vertices at the midpoints of its edges.
Coordinates
The Cartesian coordinates of the vertices of the rectified 5-cube with edge length is given by all permutations of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Coxeter plane | B2 | A3 | |
| Graph | 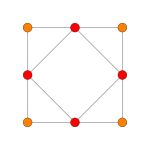
|

| |
| Dihedral symmetry |
Birectified 5-cube
| Birectified 5-cube birectified penteract (nit) | ||
|---|---|---|
| Type | uniform 5-polytope | |
| Schläfli symbol | 2r{4,3,3,3} | |
| Coxeter diagram | ||
| 4-faces | 42 | 10 32 |
| Cells | 280 | 40 160 80 |
| Faces | 640 | 320 320 |
| Edges | 480 | |
| Vertices | 80 | |
| Vertex figure |  {3}×{4} | |
| Coxeter group | B5, , order 3840 D5, , order 1920 | |
| Dual | ||
| Base point | (0,0,1,1,1,1)√2 | |
| Circumradius | sqrt(3/2) = 1.224745 | |
| Properties | convex, isogonal | |
E. L. Elte identified it in 1912 as a semiregular polytope, identifying it as Cr5 as a second rectification of a 5-dimensional cross polytope.
Alternate names
- Birectified 5-cube/penteract
- Birectified pentacross/5-orthoplex/triacontiditeron
- Penteractitriacontiditeron (acronym: nit) (Jonathan Bowers)
- Rectified 5-demicube/demipenteract
Construction and coordinates
The birectified 5-cube may be constructed by birectifying the vertices of the 5-cube at of the edge length.
The Cartesian coordinates of the vertices of a birectified 5-cube having edge length 2 are all permutations of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Coxeter plane | B2 | A3 | |
| Graph | 
|

| |
| Dihedral symmetry |
Related polytopes
| Dim. | 2 | 3 | 4 | 5 | 6 | 7 | 8 | n |
|---|---|---|---|---|---|---|---|---|
| Name | t{4} | r{4,3} | 2t{4,3,3} | 2r{4,3,3,3} | 3t{4,3,3,3,3} | 3r{4,3,3,3,3,3} | 4t{4,3,3,3,3,3,3} | ... |
| Coxeter diagram |
||||||||
| Images | 
|
 
|
 
|
 
|
 
|
 
|
 
| |
| Facets | {3} {4} |
t{3,3} t{3,4} |
r{3,3,3} r{3,3,4} |
2t{3,3,3,3} 2t{3,3,3,4} |
2r{3,3,3,3,3} 2r{3,3,3,3,4} |
3t{3,3,3,3,3,3} 3t{3,3,3,3,3,4} | ||
| Vertex figure |
( )v( ) |  { }×{ } |
 { }v{ } |
 {3}×{4} |
 {3}v{4} |
{3,3}×{3,4} | {3,3}v{3,4} |
Related polytopes
These polytopes are a part of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "5D uniform polytopes (polytera)". o3x3o3o4o - rin, o3o3x3o4o - nit
External links
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 is given by all permutations of:
is given by all permutations of: