In algebra, a resolvent cubic is one of several distinct, although related, cubic polynomials defined from a monic polynomial of degree four:
In each case:
- The coefficients of the resolvent cubic can be obtained from the coefficients of P(x) using only sums, subtractions and multiplications.
- Knowing the roots of the resolvent cubic of P(x) is useful for finding the roots of P(x) itself. Hence the name “resolvent cubic”.
- The polynomial P(x) has a multiple root if and only if its resolvent cubic has a multiple root.
Definitions
Suppose that the coefficients of P(x) belong to a field k whose characteristic is different from 2. In other words, we are working in a field in which 1 + 1 ≠ 0. Whenever roots of P(x) are mentioned, they belong to some extension K of k such that P(x) factors into linear factors in K. If k is the field Q of rational numbers, then K can be the field C of complex numbers or the field Q of algebraic numbers.
In some cases, the concept of resolvent cubic is defined only when P(x) is a quartic in depressed form—that is, when a3 = 0.
Note that the fourth and fifth definitions below also make sense and that the relationship between these resolvent cubics and P(x) are still valid if the characteristic of k is equal to 2.
First definition
Suppose that P(x) is a depressed quartic—that is, that a3 = 0. A possible definition of the resolvent cubic of P(x) is:
The origin of this definition lies in applying Ferrari's method to find the roots of P(x). To be more precise:
Add a new unknown, y, to x + a2/2. Now you have:
If this expression is a square, it can only be the square of
But the equality
is equivalent to
and this is the same thing as the assertion that R1(y) = 0.
If y0 is a root of R1(y), then it is a consequence of the computations made above that the roots of P(x) are the roots of the polynomial
together with the roots of the polynomial
Of course, this makes no sense if y0 = 0, but since the constant term of R1(y) is –a1, 0 is a root of R1(y) if and only if a1 = 0, and in this case the roots of P(x) can be found using the quadratic formula.
Second definition
Another possible definition (still supposing that P(x) is a depressed quartic) is
The origin of this definition is similar to the previous one. This time, we start by doing:
and a computation similar to the previous one shows that this last expression is a square if and only if
A simple computation shows that
Third definition
Another possible definition (again, supposing that P(x) is a depressed quartic) is
The origin of this definition lies in another method of solving quartic equations, namely Descartes' method. If you try to find the roots of P(x) by expressing it as a product of two monic quadratic polynomials x + αx + β and x – αx + γ, then
If there is a solution of this system with α ≠ 0 (note that if a1 ≠ 0, then this is automatically true for any solution), the previous system is equivalent to
It is a consequence of the first two equations that then
and
After replacing, in the third equation, β and γ by these values one gets that
and this is equivalent to the assertion that α is a root of R3(y). So, again, knowing the roots of R3(y) helps to determine the roots of P(x).
Note that
Fourth definition
Still another possible definition is
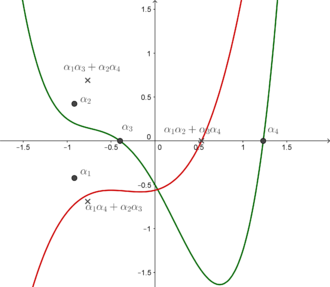
In fact, if the roots of P(x) are α1, α2, α3, and α4, then
a fact the follows from Vieta's formulas. In other words, R4(y) is the monic polynomial whose roots are α1α2 + α3α4, α1α3 + α2α4, and α1α4 + α2α3.
It is easy to see that
Therefore, P(x) has a multiple root if and only if R4(y) has a multiple root. More precisely, P(x) and R4(y) have the same discriminant.
One should note that if P(x) is a depressed polynomial, then
Fifth definition
Yet another definition is
If, as above, the roots of P(x) are α1, α2, α3, and α4, then
again as a consequence of Vieta's formulas. In other words, R5(y) is the monic polynomial whose roots are (α1 + α2)(α3 + α4), (α1 + α3)(α2 + α4), and (α1 + α4)(α2 + α3).
It is easy to see that
Therefore, as it happens with R4(y), P(x) has a multiple root if and only if R5(y) has a multiple root. More precisely, P(x) and R5(y) have the same discriminant. This is also a consequence of the fact that R5(y + a2) = -R4(-y).
Note that if P(x) is a depressed polynomial, then
Applications
Solving quartic equations
It was explained above how R1(y), R2(y), and R3(y) can be used to find the roots of P(x) if this polynomial is depressed. In the general case, one simply has to find the roots of the depressed polynomial P(x − a3/4). For each root x0 of this polynomial, x0 − a3/4 is a root of P(x).
Factoring quartic polynomials
If a quartic polynomial P(x) is reducible in k, then it is the product of two quadratic polynomials or the product of a linear polynomial by a cubic polynomial. This second possibility occurs if and only if P(x) has a root in k. In order to determine whether or not P(x) can be expressed as the product of two quadratic polynomials, let us assume, for simplicity, that P(x) is a depressed polynomial. Then it was seen above that if the resolvent cubic R3(y) has a non-null root of the form α, for some α ∈ k, then such a decomposition exists.
This can be used to prove that, in R, every quartic polynomial without real roots can be expressed as the product of two quadratic polynomials. Let P(x) be such a polynomial. We can assume without loss of generality that P(x) is monic. We can also assume without loss of generality that it is a reduced polynomial, because P(x) can be expressed as the product of two quadratic polynomials if and only if P(x − a3/4) can and this polynomial is a reduced one. Then R3(y) = y + 2a2y + (a2 − 4a0)y − a1. There are two cases:
- If a1 ≠ 0 then R3(0) = −a1 < 0. Since R3(y) > 0 if y is large enough, then, by the intermediate value theorem, R3(y) has a root y0 with y0 > 0. So, we can take α = √y0.
- If a1 = 0, then R3(y) = y + 2a2y + (a2 − 4a0)y. The roots of this polynomial are 0 and the roots of the quadratic polynomial y + 2a2y + a2 − 4a0. If a2 − 4a0 < 0, then the product of the two roots of this polynomial is smaller than 0 and therefore it has a root greater than 0 (which happens to be −a2 + 2√a0) and we can take α as the square root of that root. Otherwise, a2 − 4a0 ≥ 0 and then,
More generally, if k is a real closed field, then every quartic polynomial without roots in k can be expressed as the product of two quadratic polynomials in k. Indeed, this statement can be expressed in first-order logic and any such statement that holds for R also holds for any real closed field.
A similar approach can be used to get an algorithm to determine whether or not a quartic polynomial P(x) ∈ Q is reducible and, if it is, how to express it as a product of polynomials of smaller degree. Again, we will suppose that P(x) is monic and depressed. Then P(x) is reducible if and only if at least one of the following conditions holds:
- The polynomial P(x) has a rational root (this can be determined using the rational root theorem).
- The resolvent cubic R3(y) has a root of the form α, for some non-null rational number α (again, this can be determined using the rational root theorem).
- The number a2 − 4a0 is the square of a rational number and a1 = 0.
Indeed:
- If P(x) has a rational root r, then P(x) is the product of x − r by a cubic polynomial in Q, which can be determined by polynomial long division or by Ruffini's rule.
- If there is a rational number α ≠ 0 such that α is a root of R3(y), it was shown above how to express P(x) as the product of two quadratic polynomials in Q.
- Finally, if the third condition holds and if δ ∈ Q is such that δ = a2 − 4a0, then P(x) = (x + (a2 + δ)/2)(x + (a2 − δ)/2).
Galois groups of irreducible quartic polynomials
The resolvent cubic of an irreducible quartic polynomial P(x) can be used to determine its Galois group G; that is, the Galois group of the splitting field of P(x). Let m be the degree over k of the splitting field of the resolvent cubic (it can be either R4(y) or R5(y); they have the same splitting field). Then the group G is a subgroup of the symmetric group S4. More precisely:
- If m = 1 (that is, if the resolvent cubic factors into linear factors in k), then G is the group {e, (12)(34), (13)(24), (14)(23)}.
- If m = 2 (that is, if the resolvent cubic has one and, up to multiplicity, only one root in k), then, in order to determine G, one can determine whether or not P(x) is still irreducible after adjoining to the field k the roots of the resolvent cubic. If not, then G is a cyclic group of order 4; more precisely, it is one of the three cyclic subgroups of S4 generated by any of its six 4-cycles. If it is still irreducible, then G is one of the three subgroups of S4 of order 8, each of which is isomorphic to the dihedral group of order 8.
- If m = 3, then G is the alternating group A4.
- If m = 6, then G is the whole group S4.
See also
References
- ^ Tignol, Jean-Pierre (2016), "Quartic equations", Galois' Theory of algebraic equations (2nd ed.), World Scientific, ISBN 978-981-4704-69-4, Zbl 1333.12001
- ^ Brookfield, G. (2007), "Factoring quartic polynomials: A lost art" (PDF), Mathematics Magazine, 80 (1): 67–70, doi:10.1080/0025570X.2007.11953453, JSTOR 27642994, S2CID 53375377, Zbl 1227.97040, archived from the original (PDF) on 2015-02-21
- Hartshorne, Robin (1997), "Construction problems and field extensions: Cubic and quartic equations", Geometry: Euclid and Beyond, Springer-Verlag, ISBN 0-387-98650-2, Zbl 0954.51001
- ^ Kaplansky, Irving (1972), "Fields: Cubic and quartic equations", Fields and Rings, Chicago Lectures in Mathematics (2nd ed.), University of Chicago Press, ISBN 0-226-42451-0, Zbl 1001.16500
- Rotman, Joseph (1998), "Galois groups of quadratics, cubics, and quartics", Galois Theory (2nd ed.), Springer-Verlag, ISBN 0-387-98541-7, Zbl 0924.12001
- van der Waerden, Bartel Leendert (1991), "The Galois theory: Equations of the second, third, and fourth degrees", Algebra, vol. 1 (7th ed.), Springer-Verlag, ISBN 0-387-97424-5, Zbl 0724.12001
































