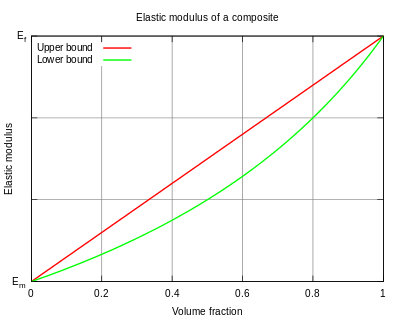
In materials science, a general rule of mixtures is a weighted mean used to predict various properties of a composite material . It provides a theoretical upper- and lower-bound on properties such as the elastic modulus, ultimate tensile strength, thermal conductivity, and electrical conductivity. In general there are two models, one for axial loading (Voigt model), and one for transverse loading (Reuss model).
In general, for some material property (often the elastic modulus), the rule of mixtures states that the overall property in the direction parallel to the fibers may be as high as
where
- is the volume fraction of the fibers
- is the material property of the fibers
- is the material property of the matrix
In the case of the elastic modulus, this is known as the upper-bound modulus, and corresponds to loading parallel to the fibers. The inverse rule of mixtures states that in the direction perpendicular to the fibers, the elastic modulus of a composite can be as low as
If the property under study is the elastic modulus, this quantity is called the lower-bound modulus, and corresponds to a transverse loading.
Derivation for elastic modulus
Voigt Modulus
Consider a composite material under uniaxial tension . If the material is to stay intact, the strain of the fibers, must equal the strain of the matrix, . Hooke's law for uniaxial tension hence gives
| 1 |
where , , , are the stress and elastic modulus of the fibers and the matrix, respectively. Noting stress to be a force per unit area, a force balance gives that
| 2 |
where is the volume fraction of the fibers in the composite (and is the volume fraction of the matrix).
If it is assumed that the composite material behaves as a linear-elastic material, i.e., abiding Hooke's law for some elastic modulus of the composite and some strain of the composite , then equations 1 and 2 can be combined to give
Finally, since , the overall elastic modulus of the composite can be expressed as
Reuss modulus
Now let the composite material be loaded perpendicular to the fibers, assuming that . The overall strain in the composite is distributed between the materials such that
The overall modulus in the material is then given by
since , .
Other properties
Similar derivations give the rules of mixtures for
- mass density: where f is the atomic percent of fiber in the mixture.
- ultimate tensile strength:
- thermal conductivity:
- electrical conductivity:
See also
When considering the empirical correlation of some physical properties and the chemical composition of compounds, other relationships, rules, or laws, also closely resembles the rule of mixtures:
- Amagat's law – Law of partial volumes of gases
- Gladstone–Dale equation – Optical analysis of liquids, glasses and crystals
- Kopp's law – Uses mass fraction
- Kopp–Neumann law – Specific heat for alloys
- Richmann's law – Law for the mixing temperature
- Vegard's law – Crystal lattice parameters
References
- ^ Alger, Mark. S. M. (1997). Polymer Science Dictionary (2nd ed.). Springer Publishing. ISBN 0412608707.
- ^ "Stiffness of long fibre composites". University of Cambridge. Retrieved 1 January 2013.
- ^ Askeland, Donald R.; Fulay, Pradeep P.; Wright, Wendelin J. (2010-06-21). The Science and Engineering of Materials (6th ed.). Cengage Learning. ISBN 9780495296027.
- Voigt, W. (1889). "Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper". Annalen der Physik. 274 (12): 573–587. Bibcode:1889AnP...274..573V. doi:10.1002/andp.18892741206.
- Reuss, A. (1929). "Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle". Zeitschrift für Angewandte Mathematik und Mechanik. 9 (1): 49–58. Bibcode:1929ZaMM....9...49R. doi:10.1002/zamm.19290090104.
- ^ "Derivation of the rule of mixtures and inverse rule of mixtures". University of Cambridge. Retrieved 1 January 2013.
 (often the elastic modulus), the rule of mixtures states that the overall property in the direction parallel to the fibers may be as high as
(often the elastic modulus), the rule of mixtures states that the overall property in the direction parallel to the fibers may be as high as

 is the
is the  is the material property of the fibers
is the material property of the fibers is the material property of the matrix
is the material property of the matrix
 . If the material is to stay intact, the strain of the fibers,
. If the material is to stay intact, the strain of the fibers,  must equal the strain of the matrix,
must equal the strain of the matrix,  .
. 
 ,
,  ,
, 
 is the volume fraction of the fibers in the composite (and
is the volume fraction of the fibers in the composite (and  is the volume fraction of the matrix).
is the volume fraction of the matrix).
 for some elastic modulus of the composite
for some elastic modulus of the composite  and some strain of the composite
and some strain of the composite  , then equations
, then equations 
 , the overall elastic modulus of the composite can be expressed as
, the overall elastic modulus of the composite can be expressed as

 . The overall strain in the composite is distributed between the materials such that
. The overall strain in the composite is distributed between the materials such that


 ,
,  .
.
 where f is the atomic percent of fiber in the mixture.
where f is the atomic percent of fiber in the mixture.

