| IEC 61966-2-1 Default RGB Colour Space - sRGB | |
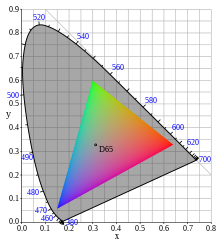 sRGB colors situated at calculated position in CIE 1931 chromaticity diagram. Luminance set so that to avoid mach bands. sRGB colors situated at calculated position in CIE 1931 chromaticity diagram. Luminance set so that to avoid mach bands. | |
| Abbreviation | sRGB |
|---|---|
| Status | Published |
| Year started | 1996 |
| First published | October 18, 1999; 25 years ago (1999-10-18) |
| Organization | IEC |
| Committee | TC/SC: TC 100/TA 2 |
| Base standards | IEC 61966 Colour Measurement and Management in Multimedia Systems and Equipment |
| Domain | Color space, color model |
| Website | webstore |
sRGB is a standard numerical encoding of colors, based on the RGB (red, green, blue) color space, for use on monitors, printers, and the World Wide Web. It was initially proposed by HP and Microsoft in 1996 and became an official standard of the International Electrotechnical Commission (IEC) as IEC 61966-2-1:1999. It is the current defined standard colorspace for the web, and it is usually the assumed colorspace for images that are neither tagged for a colorspace nor have an embedded color profile.
The sRGB standard uses the same color primaries and white point as ITU-R BT.709 standard for HDTV, but a different transfer function (or gamma) compatible with the era's CRT displays, and assumes a viewing environment closer to typical home and office viewing conditions.
The sRGB color space is also the basis of the sYCC color encoding, which is a remapping of the R, G, and B components of sRGB to a luminance (brightness) value and two chroma channels similar to those of the CIE YCbCr encoding.
sRGB definition
Gamut
| Chromaticity | Red | Green | Blue | White point |
|---|---|---|---|---|
| x | 0.6400 | 0.3000 | 0.1500 | 0.3127 |
| y | 0.3300 | 0.6000 | 0.0600 | 0.3290 |
| Y | 0.2126 | 0.7152 | 0.0722 | 1.0000 |
The sRGB standard defines the chromaticities of the red, green, and blue primaries, the colors where one of the three channels is nonzero and the other two are zero. The gamut of chromaticities that can be represented in sRGB is the color triangle defined by these primaries, which are set such that the range of colors inside the triangle is well within the range of colors visible to a human with normal trichromatic vision. As with any RGB color space, for non-negative values of R, G, and B it is not possible to represent colors outside this triangle.
The primaries come from HDTV (ITU-R BT.709), which are somewhat different from those for older color TV systems (ITU-R BT.601). These values were chosen to reflect the approximate color of consumer CRT phosphors at the time of its design. Since flat-panel displays at the time were generally designed to emulate CRT characteristics, the values also reflected prevailing practice for other display devices as well.
Transfer function ("gamma")
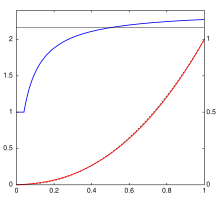

The sRGB standard specifies a non-linear encoding of physical brightness values (proportional to luminous power emitted per unit of area) into the integer R, G, and B values that are to be stored in computer memory or image files. This transfer function commonly called gamma encoding, is the combination of a linear function at low brightness values and a displaced power law for the rest of the range.
Specifically, let be the encoded R, G, or B value, assumed to be an integer ranging from 0 (meaning no light) to some maximum (meaning the maximum displayable intensity of that channel). Typically is 255 when as an 8-bit integer, or generally for an -bit integer. The physical intensity represented by is defined as , where the decoding function is defined as
where , , , and . The result is 0 for no light, and 1 for the maximum intensity. The value is sometimes called the "linear value" or "linear-light value" corresponding to the encoded sample .
Conversely, given a value between 0 and 1 that is proportional to the physical R, G, or B intensity to be displayed, the encoded integer intensity will be , where encoding function is defined as
where , and , , and are the same as in the decoding function .
These sRGB encoding and decoding functions and above are similar in form to those of BT.709, but the values are noticeably different. Because of the rounding of the parameters, they have small discontinuities at the transition between the linear and non-linear part, on the order of 10 — which are too small to matter in most practical situations.
For medium and large values of the argument , the decoding function is actually quite close to a pure power law with exponent (gamma) of 2.2. However, for low values (around and below the breakpoint ) the difference is perceptible.
If needed, the encoding and decoding functions , can be used for arguments greater than 1. They are also extended to negative values by the identities , .
In practice, there is still debate and confusion about the formulas used for encoding and decoding image colors from or into "sRGB" files. Also, programmers may choose use the "pure" power law instead of the correct piecewise formulas above, for the sake of code simplicity or efficiency, but that would introduce some issues near black. Also, some operating systems and programs may directly send sRGB encoded images to monitors which actually have a different effective decoding function, such as pure power law with 2.2 exponent, this is further complicated by the standard saying that reference CRT display should use 2.2 gamma.
Correspondence to CIE XYZ stimulus
The sRGB standard specifies also the colors and relative intensities of the three primaries R, G, and B, by defining the mapping between these values (in linear brightness scale, before the gamma encoding) and the CIE XYZ perceptual color coordinates. This mapping is the same specified by the BT.709 standard; in matrix notation,
These coefficients should be considered exact and assume the 2° standard colorimetric observer for CIE XYZ. In particular, the second row of this matrix specifies the computation of the BT.709-2 luma (brightness) value from the linear R, G, and B values. (BT.709-1 had a typo in these coefficients.)
The inverse conversion, from from CIE XYZ to (linear) sRGB, can be obtained by inverting the matrix above to a suitable numerical accuracy. The 1999 standard provides the matrix
which is not the exact inverse of the sRGB to XYZ transformation, but was expected to be accurate enough for 8-bit encoded samples (with ).
The 2003 amended version of the sRGB standard points out that higher accuracy is needed when the samples are encoded with more than 8 bits. It provides the matrix
- .
which is claimed to be sufficiently accurate for samples with bits ().
For these formulas, the X, Y, and Z values must be scaled so that the Y of D65 ("white") is 1.0 (X = 0.9505, Y = 1.0000, Z = 1.0890). This is usually true but some color spaces use 100 or other values (such as in CIELAB, when using specified white points).
Viewing environment
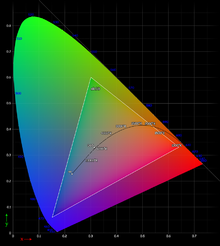
The sRGB specification assumes a dimly lit encoding (creation) environment with an ambient correlated color temperature (CCT) of 5003 K:
| Parameter | Value |
|---|---|
| Screen luminance level | 80 cd/m |
| Illuminant white point | x = 0.3127, y = 0.3290 (D65) |
| Image surround reflectance | 20% (~medium gray) |
| Encoding ambient illuminance level | 64 lux |
| Encoding ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Encoding viewing flare | 1.0% |
| Typical ambient illuminance level | 200 lux |
| Typical ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Typical viewing flare | 5.0% |
The assumed ambient CCT differs from that of the BT.709 standard illuminant (D65), which is still retained for the screen white point. Using D50 for both would have made the white point of most photographic paper appear excessively blue. The other parameters, such as the luminance level, are representative of a typical CRT monitor.
For optimal results, the ICC recommends using the encoding viewing environment (i.e., dim, diffuse lighting) rather than the less-stringent typical viewing environment.
The bg-sRGB space
Annex G of the 2003 amendment of the sRGB standard describes an alternative encoding of color values, called bg-sRGB, that is recommended when the number of bits per channel is 10 or more.
In this alternative encoding, an integer encoded sample value and the corresponding linear R, G, or B value are related by the formulas
and
where the and functions are the same as in the sRGB space. The standard specifies and for , and generally
for . In the bg-sRGB color space, the null intensity is encoded as the integer , and the maximum displayable intensity is encoded as the integer . This encoding is useful for color space manipulations (like the conversion from sYCC) that can generate values that are negative or greater than 1.
History
The non-linear encoding of physical data samples is a common digital signal processing technique that aims to make better use of the bits available for the encoded signal, taking into account the non-linear way human senses perceive physical stimuli. Using smaller increments for smaller signals reduces the quantization artifacts.
This principle was incorporated into the digital-to-analog converters and the analog circuitry of early computer monitors, resulting in an effective decoding function (the mapping from digital sample values to the displayed intensity) which was roughly a power law with an exponent between 2 and 3. The exponent was commonly denoted with the letter , hence the common name "gamma correction" (or similar) for this function. This mapping initially varied according to CRT manufacturers, but was normalized in 1993 for use in HDTV systems, as the ITU BT.709 standard The BT.709 standard specified a decoding function with a linear section near zero, transitioning to a shifted power law with exponent 1/0.45 ≈ 2.2222....
The sRGB encoding was created a few years later by Hewlett-Packard and Microsoft. It was meant to describe the decoding function of most CRT computer monitors used with Windows operating systems at the time, which was still different from that assumed by BT.709. The first draft of the standard was published in 1996. A fourth draft, still incomplete, is available online. Like the BT.709, the sRGB decoding function was defined as a linear section near zero that transitions to a shifted power law
Justification for the formulas
In theory, the parameters of the encoding and decoding functions should be chosen so that the transition from the linear section to the power law section is continuous (without a sudden step) and smooth (without a sudden change of slope).
To derive the decoding function, one considers that the general formula for a linear function, whose graph is a straight line that passes through (0,0), is , and a shifted power law curve that passes through (1,1) is
To obtain a seamless transition between the two functions when has a value , we must have
To avoid a sudden change of slope where the two segments meet, the derivatives must be equal at this point:
Solving the two equations for and we get
Parameter values
The first draft of the sRGB standard initially set the parameters at and so that the resulting decoding function closely resembled a pure power law with exponent (gamma) 2.2, assimed to be typical of computer monitors at the time. This choice implies a breakpoint and a linear coefficient . These values, rounded to and are still incorrectly given in some publications. However, the value of was rounded to already in the sRGB draft standard, resulting in a small discontinuity in the curve.
The first official version of the standard was defined and published by the IEC in 1999. In this version, the rounded value of was retained, but the breakpoint was redefined as to make the curve approximately continuous. With these values, there is still a discontinuity in the slope, from just below the intersection to just above it. The final standard also corrected some small rounding errors present in the draft.
The 1999 IEC standard was amended in 2003. The sRGB to CIE XYZ matrix was retained, but the inverse transformation above was replaced by a more accurate version, with seven decimal fraction digits. The amended standard also included the definition of the sYCC encoding, using brightness (Y) and two chroma coordinates (CC) instead of R, G, and B coordinates, and a bg-sRGB encoding for 10-bit components which allows some component values outside the 0-1 range.
Usage

Due to the standardization of sRGB on the Internet, on computers, and on printers, many low- to medium-end consumer digital cameras and scanners use sRGB as the default (or only available) working color space. However, consumer-level CCDs are typically uncalibrated, meaning that even though the image or device is being labeled as "sRGB", one cannot assume that the encoded values or the colors of displayed images are accurate as specified by the standard. Recently that changed and smartphones and TVs have very good calibration out of the box.
If the color space of an image is unknown and the R, G, and B samples are encoded with 8 bits each, the sRGB encoding usually the assumed default.
As the sRGB gamut mostly meets or exceeds the gamut of a low-end inkjet printer, an sRGB image is often regarded as satisfactory for home printing. The sRGB color space is sometimes avoided by high-end print publishing professionals because its color gamut is not big enough, especially in the blue-green colors, to include all the colors that can be reproduced in CMYK printing. Images intended for professional printing via a fully color-managed workflow (e.g. prepress output) sometimes use another color space such as Adobe RGB (1998), which accommodates a wider gamut and CMYK color space like Fogra39. Such CMYK and sRGB images used on the Internet may be converted to sRGB using color management tools that are usually included with software that works in these other color spaces.
Programming interface support
The two dominant programming interfaces for 3D graphics, OpenGL and Direct3D, have both incorporated support for the sRGB gamma curve. OpenGL supports textures with sRGB gamma encoded color components (first introduced with EXT_texture_sRGB extension, added to the core in OpenGL 2.1) and rendering into sRGB gamma encoded framebuffers (first introduced with EXT_framebuffer_sRGB extension, added to the core in OpenGL 3.0). Correct mipmapping and interpolation of sRGB gamma textures has direct hardware support in texturing units of most modern GPUs (for example nVidia GeForce 8 performs conversion from 8-bit texture to linear values before interpolating those values), and does not have any performance penalty.
ICC profiles
A lookup table may be used to efficiently convert sRGB to other color spaces. The International Color Consortium (ICC) has published color profiles for this purpose, which are widely used. There are several variants, including ICCmax, version 4, and version 2.
Version 4 is generally recommended, but version 2 is still commonly used and is the most compatible with other software including browsers. However, inconsistencies have been pointed out between those ICC profiles and the IEC sRGB standard. In particular, version 2 of the ICC profile specification does not implement the piecewise parametric curve encoding ("para") as specified by the IEC sRGB standard, and has to implement the linear spline using 1DLUT. What is worse in some cases "simplified sRGB" is used which is just 2.2 gamma.
The sYCC color space
Amendment 1 to IEC 61966-2-1:1999, approved in 2003, includes the definition of a Y′Cb′Cr′ color representation called sYCC. Although the RGB color primaries are based on BT.709, the equations for transformation from sRGB to sYCC and vice versa are based on BT.601. The sYCC standard specifies 8 bits for the encoded components, and the matrices result in a range of approximately 0–1 for Y; -0.5–0.5 for C.
As this conversion can result in sRGB values outside the range 0–1, the amendment describes how to apply the gamma correction to negative values, by applying −f(−x) when x is negative (and f is the sRGB↔linear functions described above). This is also used by scRGB.
References
- ^ "IEC 61966-2-1:1999". IEC Webstore. International Electrotechnical Commission. Retrieved 3 March 2017.. The first official specification of sRGB.
- ^ Michael Stokes; Matthew Anderson; Srinivasan Chandrasekar; Ricardo Motta (November 5, 1996). "A Standard Default Color Space for the Internet – sRGB, Version 1.10". Archived from the original on Jul 3, 2023.
- Charles A. Poynton (2003). Digital Video and HDTV: Algorithms and Interfaces. Morgan Kaufmann. ISBN 1-55860-792-7.
- ^ Image Engineering GmbH (2012): "Color spaces - REC.709 vs. sRGB Online document at www.image-engineering.de. Includes a graph comparing two transfer functions. Accessed on 2024-12-17.
- ^ "IEC 61966-2-1:1999 Multimedia systems and equipment – Colour measurement and management – Part 2-1: Colour management – Default RGB colour space – sRGB: Amendment 1". International Electrotechnical Commission. 2003. Replaces the version IEC 61966-2-1:1999, introducing the sYCC encoding for YCbCr color spaces, an extended-gamut RGB encoding bg-sRGB, and a CIELAB transformation.
- Jason Summers (2012): "A close look at the sRGB formula". Online document at entropymine.com. Accessed on 2014-12-17 (archived)
- ^ Daniele Siragusano (2020): "Colour Online: sRGB... We Need To Talk". YouTube video of talk (2020-07-17, 57 min) discussing mismatch between sRGB and actual monitor transfer functions. Posted in channel @FilmLight. Accessed on 2024-12-17.
- Jon Y. Hardeberg (2001). Acquisition and Reproduction of Color Images: Colorimetric and Multispectral Approaches. Universal-Publishers.com. ISBN 1-58112-135-0.
- Conversion matrices for RGB vs. XYZ conversion by Bruce Justin Lindbloom
- ^ International Color Consortium (2015): "How to interpret the sRGB color space (specified in IEC 61966-2-1) for ICC profiles". Online document at www.color.org. Accessed on 2024-12-17 (archived)
- Rodney, Andrew (2005). Color Management for Photographers. Focal Press. p. 121. ISBN 978-0-240-80649-5.
- "Why Calibrate Monitor to D65 When Light Booth is D50". X-Rite. Retrieved 2022-09-11.
- ^ International Color Consortium (undated): "sRGB" Summary page at color.org. Accessed on 2014-12-17 (archiving failed).
- "BT.709 : Parameter values for the HDTV standards for production and international programme exchange". www.itu.net. n.d. Retrieved 2021-04-19.
- ^ sRGB.com Notes on design and use of sRGB (archived) by HP.
- fourth working draft (4WD) for 2CD of IEC 61966-2-1, (archived). Still not the complete standard.
- Roberts, A. BBC RD 1991/6 Methods of Measuring and Calculating Display Transfer Characteristics (PDF) (Report). BBC. p. 1.
- NumFocus Colour Science (2015): "The Importance of Terminology and sRGB Uncertainty". Online document at www.colour-science.org, dated 2015-12-05. Accessed on 2024-12-17 (archived).
- Phil Green & Lindsay W. MacDonald (2002). Colour Engineering: Achieving Device Independent Colour. John Wiley and Sons. ISBN 0-471-48688-4.
- "EXT_texture_sRGB". 24 January 2007. Retrieved 12 May 2020.
- "EXT_framebuffer_sRGB". 17 September 2010. Retrieved 12 May 2020.
- "GPU Gems 3: Chapter 24. The Importance of Being Linear, section 24.4.1". NVIDIA Corporation. Retrieved 3 March 2017.
- ^ International Color Consortium (undated): "sRGB profiles". Summary page at color.org. Accessed on 2014-12-17 (archiving failed).
- "Is your system ICC Version 4 ready?". www.color.org. Retrieved 2024-12-21.
- Will the Real sRGB Profile Please Stand Up? by Elle Stone. Analyzes the inconsistency among sRGB ICC profiles
- "Android lock screen bug and ICC profiles". color.org. Retrieved 2024-12-25.
- Developers, Colour (2019-10-25). "sRGB EOTF: Pure Gamma 2.2 Function or Piece-Wise Function?". Colour Science. Retrieved 2024-12-25.
External links
| Color space | |
|---|---|
| CAM | |
| CIE | |
| RGB | |
| Y′UV | |
| Other | |
| Color systems and standards | |
| For the vision capacities of organisms or machines, see | |
 set so that
set so that  to avoid
to avoid  be the encoded R, G, or B value, assumed to be an integer ranging from 0 (meaning no light) to some maximum
be the encoded R, G, or B value, assumed to be an integer ranging from 0 (meaning no light) to some maximum  (meaning the maximum displayable intensity of that channel). Typically
(meaning the maximum displayable intensity of that channel). Typically  for an
for an  -bit integer. The physical intensity represented by
-bit integer. The physical intensity represented by  , where the decoding function
, where the decoding function  is defined as
is defined as

 ,
,  ,
,  , and
, and  . The result is 0 for no light, and 1 for the maximum intensity. The value
. The result is 0 for no light, and 1 for the maximum intensity. The value  between 0 and 1 that is proportional to the physical R, G, or B intensity to be displayed, the encoded integer intensity will be
between 0 and 1 that is proportional to the physical R, G, or B intensity to be displayed, the encoded integer intensity will be  , where encoding function
, where encoding function  is defined as
is defined as

 , and
, and  ,
,  , and
, and  are the same as in the decoding function
are the same as in the decoding function  , the decoding function
, the decoding function  ) the difference is perceptible.
) the difference is perceptible.
 ,
,  .
.
 instead of the correct piecewise formulas above, for the sake of code simplicity or efficiency, but that would introduce some issues near black. Also, some operating systems and programs may directly send sRGB encoded images to monitors which actually have a different effective decoding function, such as pure power law with 2.2 exponent, this is further complicated by the standard saying that reference CRT display should use 2.2 gamma.
instead of the correct piecewise formulas above, for the sake of code simplicity or efficiency, but that would introduce some issues near black. Also, some operating systems and programs may directly send sRGB encoded images to monitors which actually have a different effective decoding function, such as pure power law with 2.2 exponent, this is further complicated by the standard saying that reference CRT display should use 2.2 gamma.


 ).
).
 .
. bits (
bits ( ).
).


 and
and  for
for  , and generally
, and generally

 .
In the bg-sRGB color space, the null intensity
.
In the bg-sRGB color space, the null intensity  is encoded as the integer
is encoded as the integer  , and the maximum displayable intensity
, and the maximum displayable intensity  is encoded as the integer
is encoded as the integer  . This encoding is useful for color space manipulations (like the conversion from sYCC) that can generate values
. This encoding is useful for color space manipulations (like the conversion from sYCC) that can generate values  , hence the common name "gamma correction" (or similar) for this function. This mapping initially varied according to CRT manufacturers, but was normalized in 1993 for use in HDTV systems, as the
, hence the common name "gamma correction" (or similar) for this function. This mapping initially varied according to CRT manufacturers, but was normalized in 1993 for use in HDTV systems, as the  , and a shifted power law curve that passes through (1,1) is
, and a shifted power law curve that passes through (1,1) is 
 has a value
has a value 


 and a linear coefficient
and a linear coefficient  . These values, rounded to
. These values, rounded to  and
and  are still incorrectly given in some publications. However, the value of
are still incorrectly given in some publications. However, the value of  already in the sRGB draft standard, resulting in a small discontinuity in the curve.
already in the sRGB draft standard, resulting in a small discontinuity in the curve.
 to make the curve approximately continuous. With these values, there is still a discontinuity in the slope, from
to make the curve approximately continuous. With these values, there is still a discontinuity in the slope, from  just below the intersection to
just below the intersection to  just above it. The final standard also corrected some small rounding errors present in the draft.
just above it. The final standard also corrected some small rounding errors present in the draft.