In biology, a substitution model, also called models of sequence evolution, are Markov models that describe changes over evolutionary time. These models describe evolutionary changes in macromolecules, such as DNA sequences or protein sequences, that can be represented as sequence of symbols (e.g., A, C, G, and T in the case of DNA or the 20 "standard" proteinogenic amino acids in the case of proteins). Substitution models are used to calculate the likelihood of phylogenetic trees using multiple sequence alignment data. Thus, substitution models are central to maximum likelihood estimation of phylogeny as well as Bayesian inference in phylogeny. Estimates of evolutionary distances (numbers of substitutions that have occurred since a pair of sequences diverged from a common ancestor) are typically calculated using substitution models (evolutionary distances are used as input for distance methods such as neighbor joining). Substitution models are also central to phylogenetic invariants because they are necessary to predict site pattern frequencies given a tree topology. Substitution models are also necessary to simulate sequence data for a group of organisms related by a specific tree.
Phylogenetic tree topologies and other parameters
Phylogenetic tree topologies are often the parameter of interest; thus, branch lengths and any other parameters describing the substitution process are often viewed as nuisance parameters. However, biologists are sometimes interested in the other aspects of the model. For example, branch lengths, especially when those branch lengths are combined with information from the fossil record and a model to estimate the timeframe for evolution. Other model parameters have been used to gain insights into various aspects of the process of evolution. The Ka/Ks ratio (also called ω in codon substitution models) is a parameter of interest in many studies. The Ka/Ks ratio can be used to examine the action of natural selection on protein-coding regions, it provides information about the relative rates of nucleotide substitutions that change amino acids (non-synonymous substitutions) to those that do not change the encoded amino acid (synonymous substitutions).
Application to sequence data
Most of the work on substitution models has focused on DNA/RNA and protein sequence evolution. Models of DNA sequence evolution, where the alphabet corresponds to the four nucleotides (A, C, G, and T), are probably the easiest models to understand. DNA models can also be used to examine RNA virus evolution; this reflects the fact that RNA also has a four nucleotide alphabet (A, C, G, and U). However, substitution models can be used for alphabets of any size; the alphabet is the 20 proteinogenic amino acids for proteins and the sense codons (i.e., the 61 codons that encode amino acids in the standard genetic code) for aligned protein-coding gene sequences. In fact, substitution models can be developed for any biological characters that can be encoded using a specific alphabet (e.g., amino acid sequences combined with information about the conformation of those amino acids in three-dimensional protein structures).
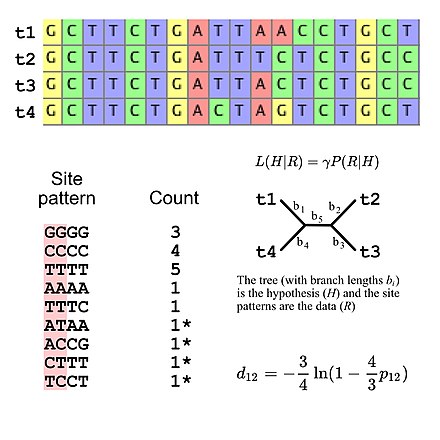
The majority of substitution models used for evolutionary research assume independence among sites (i.e., the probability of observing any specific site pattern is identical regardless of where the site pattern is in the sequence alignment). This simplifies likelihood calculations because it is only necessary to calculate the probability of all site patterns that appear in the alignment then use those values to calculate the overall likelihood of the alignment (e.g., the probability of three "GGGG" site patterns given some model of DNA sequence evolution is simply the probability of a single "GGGG" site pattern raised to the third power). This means that substitution models can be viewed as implying a specific multinomial distribution for site pattern frequencies. If we consider a multiple sequence alignment of four DNA sequences there are 256 possible site patterns so there are 255 degrees of freedom for the site pattern frequencies. However, it is possible to specify the expected site pattern frequencies using five degrees of freedom if using the Jukes-Cantor model of DNA evolution, which is a simple substitution model that allows one to calculate the expected site pattern frequencies only the tree topology and the branch lengths (given four taxa an unrooted bifurcating tree has five branch lengths).
Substitution models also make it possible to simulate sequence data using Monte Carlo methods. Simulated multiple sequence alignments can be used to assess the performance of phylogenetic methods and generate the null distribution for certain statistical tests in the fields of molecular evolution and molecular phylogenetics. Examples of these tests include tests of model fit and the "SOWH test" that can be used to examine tree topologies.
Application to morphological data
The fact that substitution models can be used to analyze any biological alphabet has made it possible to develop models of evolution for phenotypic datasets (e.g., morphological and behavioural traits). Typically, "0" is. used to indicate the absence of a trait and "1" is used to indicate the presence of a trait, although it is also possible to score characters using multiple states. Using this framework, we might encode a set of phenotypes as binary strings (this could be generalized to k-state strings for characters with more than two states) before analyses using an appropriate mode. This can be illustrated using a "toy" example: we can use a binary alphabet to score the following phenotypic traits "has feathers", "lays eggs", "has fur", "is warm-blooded", and "capable of powered flight". In this toy example hummingbirds would have sequence 11011 (most other birds would have the same string), ostriches would have the sequence 11010, cattle (and most other land mammals) would have 00110, and bats would have 00111. The likelihood of a phylogenetic tree can then be calculated using those binary sequences and an appropriate substitution model. The existence of these morphological models make it possible to analyze data matrices with fossil taxa, either using the morphological data alone or a combination of morphological and molecular data (with the latter scored as missing data for the fossil taxa).
There is an obvious similarity between use of molecular or phenotypic data in the field of cladistics and analyses of morphological characters using a substitution model. However, there has been a vociferous debate in the systematics community regarding the question of whether or not cladistic analyses should be viewed as "model-free". The field of cladistics (defined in the strictest sense) favor the use of the maximum parsimony criterion for phylogenetic inference. Many cladists reject the position that maximum parsimony is based on a substitution model and (in many cases) they justify the use of parsimony using the philosophy of Karl Popper. However, the existence of "parsimony-equivalent" models (i.e., substitution models that yield the maximum parsimony tree when used for analyses) makes it possible to view parsimony as a substitution model.
The molecular clock and the units of time
Typically, a branch length of a phylogenetic tree is expressed as the expected number of substitutions per site; if the evolutionary model indicates that each site within an ancestral sequence will typically experience x substitutions by the time it evolves to a particular descendant's sequence then the ancestor and descendant are considered to be separated by branch length x.
Sometimes a branch length is measured in terms of geological years. For example, a fossil record may make it possible to determine the number of years between an ancestral species and a descendant species. Because some species evolve at faster rates than others, these two measures of branch length are not always in direct proportion. The expected number of substitutions per site per year is often indicated with the Greek letter mu (μ).
A model is said to have a strict molecular clock if the expected number of substitutions per year μ is constant regardless of which species' evolution is being examined. An important implication of a strict molecular clock is that the number of expected substitutions between an ancestral species and any of its present-day descendants must be independent of which descendant species is examined.
Note that the assumption of a strict molecular clock is often unrealistic, especially across long periods of evolution. For example, even though rodents are genetically very similar to primates, they have undergone a much higher number of substitutions in the estimated time since divergence in some regions of the genome. This could be due to their shorter generation time, higher metabolic rate, increased population structuring, increased rate of speciation, or smaller body size. When studying ancient events like the Cambrian explosion under a molecular clock assumption, poor concurrence between cladistic and phylogenetic data is often observed. There has been some work on models allowing variable rate of evolution.
Models that can take into account variability of the rate of the molecular clock between different evolutionary lineages in the phylogeny are called “relaxed” in opposition to “strict”. In such models the rate can be assumed to be correlated or not between ancestors and descendants and rate variation among lineages can be drawn from many distributions but usually exponential and lognormal distributions are applied. There is a special case, called “local molecular clock” when a phylogeny is divided into at least two partitions (sets of lineages) and a strict molecular clock is applied in each, but with different rates.
Time-reversible and stationary models
Many useful substitution models are time-reversible; in terms of the mathematics, the model does not care which sequence is the ancestor and which is the descendant so long as all other parameters (such as the number of substitutions per site that is expected between the two sequences) are held constant.
When an analysis of real biological data is performed, there is generally no access to the sequences of ancestral species, only to the present-day species. However, when a model is time-reversible, which species was the ancestral species is irrelevant. Instead, the phylogenetic tree can be rooted using any of the species, re-rooted later based on new knowledge, or left unrooted. This is because there is no 'special' species, all species will eventually derive from one another with the same probability.
A model is time reversible if and only if it satisfies the property (the notation is explained below)
or, equivalently, the detailed balance property,
for every i, j, and t.
Time-reversibility should not be confused with stationarity. A model is stationary if Q does not change with time. The analysis below assumes a stationary model.
The mathematics of substitution models
Stationary, neutral, independent, finite sites models (assuming a constant rate of evolution) have two parameters, π, an equilibrium vector of base (or character) frequencies and a rate matrix, Q, which describes the rate at which bases of one type change into bases of another type; element for i ≠ j is the rate at which base i goes to base j. The diagonals of the Q matrix are chosen so that the rows sum to zero:
The equilibrium row vector π must be annihilated by the rate matrix Q:
The transition matrix function is a function from the branch lengths (in some units of time, possibly in substitutions), to a matrix of conditional probabilities. It is denoted . The entry in the i column and the j row, , is the probability, after time t, that there is a base j at a given position, conditional on there being a base i in that position at time 0. When the model is time reversible, this can be performed between any two sequences, even if one is not the ancestor of the other, if you know the total branch length between them.
The asymptotic properties of Pij(t) are such that Pij(0) = δij, where δij is the Kronecker delta function. That is, there is no change in base composition between a sequence and itself. At the other extreme, or, in other words, as time goes to infinity the probability of finding base j at a position given there was a base i at that position originally goes to the equilibrium probability that there is base j at that position, regardless of the original base. Furthermore, it follows that for all t.
The transition matrix can be computed from the rate matrix via matrix exponentiation:
where Q is the matrix Q multiplied by itself enough times to give its n power.
If Q is diagonalizable, the matrix exponential can be computed directly: let Q = U Λ U be a diagonalization of Q, with
where Λ is a diagonal matrix and where are the eigenvalues of Q, each repeated according to its multiplicity. Then
where the diagonal matrix e is given by
Generalised time reversible
Generalised time reversible (GTR) is the most general neutral, independent, finite-sites, time-reversible model possible. It was first described in a general form by Simon Tavaré in 1986. The GTR model is often called the general time reversible model in publications; it has also been called the REV model.
The GTR parameters for nucleotides consist of an equilibrium base frequency vector, , giving the frequency at which each base occurs at each site, and the rate matrix
Because the model must be time reversible and must approach the equilibrium nucleotide (base) frequencies at long times, each rate below the diagonal equals the reciprocal rate above the diagonal multiplied by the equilibrium ratio of the two bases. As such, the nucleotide GTR requires 6 substitution rate parameters and 4 equilibrium base frequency parameters. Since the 4 frequency parameters must sum to 1, there are only 3 free frequency parameters. The total of 9 free parameters is often further reduced to 8 parameters plus , the overall number of substitutions per unit time. When measuring time in substitutions (=1) only 8 free parameters remain.
In general, to compute the number of parameters, you count the number of entries above the diagonal in the matrix, i.e. for n trait values per site , and then add n-1 for the equilibrium frequencies, and subtract 1 because is fixed. You get
For example, for an amino acid sequence (there are 20 "standard" amino acids that make up proteins), you would find there are 208 parameters. However, when studying coding regions of the genome, it is more common to work with a codon substitution model (a codon is three bases and codes for one amino acid in a protein). There are codons, resulting in 2078 free parameters. However, the rates for transitions between codons which differ by more than one base are often assumed to be zero, reducing the number of free parameters to only parameters. Another common practice is to reduce the number of codons by forbidding the stop (or nonsense) codons. This is a biologically reasonable assumption because including the stop codons would mean that one is calculating the probability of finding sense codon after time given that the ancestral codon is would involve the possibility of passing through a state with a premature stop codon.
An alternative (and commonly used) way to write the instantaneous rate matrix ( matrix) for the nucleotide GTR model is:
The matrix is normalized so .
This notation is easier to understand than the notation originally used by Tavaré, because all model parameters correspond either to "exchangeability" parameters ( through , which can also be written using the notation ) or to equilibrium nucleotide frequencies . Note that the nucleotides in the matrix have been written in alphabetical order. In other words, the transition probability matrix for the matrix above would be:
Some publications write the nucleotides in a different order (e.g., some authors choose to group two purines together and the two pyrimidines together; see also models of DNA evolution). These differences in notation make it important to be clear regarding the order of the states when writing the matrix.
The value of this notation is that instantaneous rate of change from nucleotide to nucleotide can always be written as , where is the exchangeability of nucleotides and and is the equilibrium frequency of the nucleotide. The matrix shown above uses the letters through for the exchangeability parameters in the interest of readability, but those parameters could also be to written in a systematic manner using the notation (e.g., , , and so forth).
Note that the ordering of the nucleotide subscripts for exchangeability parameters is irrelevant (e.g., ) but the transition probability matrix values are not (i.e., is the probability of observing A in sequence 1 and C in sequence 2 when the evolutionary distance between those sequences is whereas is the probability of observing C in sequence 1 and A in sequence 2 at the same evolutionary distance).
An arbitrarily chosen exchangeability parameters (e.g., ) is typically set to a value of 1 to increase the readability of the exchangeability parameter estimates (since it allows users to express those values relative to chosen exchangeability parameter). The practice of expressing the exchangeability parameters in relative terms is not problematic because the matrix is normalized. Normalization allows (time) in the matrix exponentiation to be expressed in units of expected substitutions per site (standard practice in molecular phylogenetics). This is the equivalent to the statement that one is setting the mutation rate to 1) and reducing the number of free parameters to eight. Specifically, there are five free exchangeability parameters ( through , which are expressed relative to the fixed in this example) and three equilibrium base frequency parameters (as described above, only three values need to be specified because must sum to 1).
The alternative notation also makes it easier to understand the sub-models of the GTR model, which simply correspond to cases where exchangeability and/or equilibrium base frequency parameters are constrained to take on equal values. A number of specific sub-models have been named, largely based on their original publications:
| Model | Exchangeability parameters | Base frequency parameters | Reference |
|---|---|---|---|
| JC69 (or JC) | Jukes and Cantor (1969) | ||
| F81 | all values free | Felsenstein (1981) | |
| K2P (or K80) | (transversions), (transitions) | Kimura (1980) | |
| HKY85 | (transversions), (transitions) | all values free | Hasegawa et al. (1985) |
| K3ST (or K81) | ( transversions), ( transversions), (transitions) | Kimura (1981) | |
| TN93 | (transversions), ( transitions), ( transitions) | all values free | Tamura and Nei (1993) |
| SYM | all exchangeability parameters free | Zharkikh (1994) | |
| GTR (or REV) | all exchangeability parameters free | all values free | Tavaré (1986) |
There are 203 possible ways that the exchangeability parameters can be restricted to form sub-models of GTR, ranging from the JC69 and F81 models (where all exchangeability parameters are equal) to the SYM model and the full GTR (or REV) model (where all exchangeability parameters are free). The equilibrium base frequencies are typically treated in two different ways: 1) all values are constrained to be equal (i.e., ); or 2) all values are treated as free parameters. Although the equilibrium base frequencies can be constrained in other ways most constraints that link some but not all values are unrealistic from a biological standpoint. The possible exception is enforcing strand symmetry (i.e., constraining and but allowing ).
The alternative notation also makes it straightforward to see how the GTR model can be applied to biological alphabets with a larger state-space (e.g., amino acids or codons). It is possible to write a set of equilibrium state frequencies as , , ... and a set of exchangeability parameters () for any alphabet of character states. These values can then be used to populate the matrix by setting the off-diagonal elements as shown above (the general notation would be ), setting the diagonal elements to the negative sum of the off-diagonal elements on the same row, and normalizing. Obviously, for amino acids and for codons (assuming the standard genetic code). However, the generality of this notation is beneficial because one can use reduced alphabets for amino acids. For example, one can use and encode amino acids by recoding the amino acids using the six categories proposed by Margaret Dayhoff. Reduced amino acid alphabets are viewed as a way to reduce the impact of compositional variation and saturation.
Importantly, evolutionary patterns can vary among genomic regions and thus different genomic regions can fit with different substitution models. Actually, ignoring heterogeneous evolutionary patterns along sequences can lead to biases in the estimation of evolutionary parameters, including the Ka/Ks ratio. In this regard, the use of mixture models in phylogenentic frameworks is convenient to better mimic the molecular evolution observed in real data.
Mechanistic vs. empirical models
A main difference in evolutionary models is how many parameters are estimated every time for the data set under consideration and how many of them are estimated once on a large data set. Mechanistic models describe all substitutions as a function of a number of parameters which are estimated for every data set analyzed, preferably using maximum likelihood. This has the advantage that the model can be adjusted to the particularities of a specific data set (e.g. different composition biases in DNA). Problems can arise when too many parameters are used, particularly if they can compensate for each other (this can lead to non-identifiability). Then it is often the case that the data set is too small to yield enough information to estimate all parameters accurately.
Empirical models are created by estimating many parameters (typically all entries of the rate matrix as well as the character frequencies, see the GTR model above) from a large data set. These parameters are then fixed and will be reused for every data set. This has the advantage that those parameters can be estimated more accurately. Normally, it is not possible to estimate all entries of the substitution matrix from the current data set only. On the downside, the parameters estimated from the training data might be too generic and therefore have a poor fit to any particular dataset. A potential solution for that problem is to estimate some parameters from the data using maximum likelihood (or some other method). In studies of protein evolution the equilibrium amino acid frequencies (using the one-letter IUPAC codes for amino acids to indicate their equilibrium frequencies) are often estimated from the data while keeping the exchangeability matrix fixed. Beyond the common practice of estimating amino acid frequencies from the data, methods to estimate exchangeability parameters or adjust the matrix for protein evolution in other ways have been proposed.
With the large-scale genome sequencing still producing very large amounts of DNA and protein sequences, there is enough data available to create empirical models with any number of parameters, including empirical codon models. Because of the problems mentioned above, the two approaches are often combined, by estimating most of the parameters once on large-scale data, while a few remaining parameters are then adjusted to the data set under consideration. The following sections give an overview of the different approaches taken for DNA, protein or codon-based models.
DNA substitution models
Main article: Models of DNA evolutionThe first models of DNA evolution was proposed Jukes and Cantor in 1969. The Jukes-Cantor (JC or JC69) model assumes equal transition rates as well as equal equilibrium frequencies for all bases and it is the simplest sub-model of the GTR model. In 1980, Motoo Kimura introduced a model with two parameters (K2P or K80): one for the transition and one for the transversion rate. A year later, Kimura introduced a second model (K3ST, K3P, or K81) with three substitution types: one for the transition rate, one for the rate of transversions that conserve the strong/weak properties of nucleotides ( and , designated by Kimura), and one for rate of transversions that conserve the amino/keto properties of nucleotides ( and , designated by Kimura). In 1981, Joseph Felsenstein proposed a four-parameter model (F81) in which the substitution rate corresponds to the equilibrium frequency of the target nucleotide. Hasegawa, Kishino, and Yano unified the two last models to a five-parameter model (HKY). After these pioneering efforts, many additional sub-models of the GTR model were introduced into the literature (and common use) in the 1990s. Other models that move beyond the GTR model in specific ways were also developed and refined by several researchers.
Almost all DNA substitution models are mechanistic models (as described above). The small number of parameters that one needs to estimate for these models makes it feasible to estimate those parameters from the data. It is also necessary because the patterns of DNA sequence evolution often differ among organisms and among genes within organisms. The later may reflect optimization by the action of selection for specific purposes (e.g. fast expression or messenger RNA stability) or it might reflect neutral variation in the patterns of substitution. Thus, depending on the organism and the type of gene, it is likely necessary to adjust the model to these circumstances.
Two-state substitution models
An alternative way to analyze DNA sequence data is to recode the nucleotides as purines (R) and pyrimidines (Y); this practice is often called RY-coding. Insertions and deletions in multiple sequence alignments can also be encoded as binary data and analyzed in using a two-state model.
The simplest two-state model of sequence evolution is called the Cavender-Farris model or the Cavender-Farris-Neyman (CFN) model; the name of this model reflects the fact that it was described independently in several different publications. The CFN model is identical to the Jukes-Cantor model adapted to two states and it has even been implemented as the "JC2" model in the popular IQ-TREE software package (using this model in IQ-TREE requires coding the data as 0 and 1 rather than R and Y; the popular PAUP* software package can interpret a data matrix comprising only R and Y as data to be analyzed using the CFN model). It is also straightforward to analyze binary data using the phylogenetic Hadamard transform. The alternative two-state model allows the equilibrium frequency parameters of R and Y (or 0 and 1) to take on values other than 0.5 by adding single free parameter; this model is variously called CFu or GTR2 (in IQ-TREE).
Amino acid substitution models
For many analyses, particularly for longer evolutionary distances, the evolution is modeled on the amino acid level. Since not all DNA substitution also alter the encoded amino acid, information is lost when looking at amino acids instead of nucleotide bases. However, several advantages speak in favor of using the amino acid information: DNA is much more inclined to show compositional bias than amino acids, not all positions in the DNA evolve at the same speed (non-synonymous mutations are less likely to become fixed in the population than synonymous ones), but probably most important, because of those fast evolving positions and the limited alphabet size (only four possible states), the DNA suffers from more back substitutions, making it difficult to accurately estimate evolutionary longer distances.
Unlike the DNA models, amino acid models traditionally are empirical models. They were pioneered in the 1960s and 1970s by Dayhoff and co-workers by estimating replacement rates from protein alignments with at least 85% identity (originally with very limited data and ultimately culminating in the Dayhoff PAM model of 1978). This minimized the chances of observing multiple substitutions at a site. From the estimated rate matrix, a series of replacement probability matrices were derived, known under names such as PAM250. Log-odds matrices based on the Dayhoff PAM model were commonly used to assess the significance of homology search results, although the BLOSUM matrices have superseded the PAM log-odds matrices in this context because the BLOSUM matrices appear to be more sensitive across a variety of evolutionary distances, unlike the PAM log-odds matrices.
The Dayhoff PAM matrix was the source of the exchangeability parameters used in one of the first maximum-likelihood analyses of phylogeny that used protein data and the PAM model (or an improved version of the PAM model called DCMut) continues to be used in phylogenetics. However, the limited number of alignments used to generate the PAM model (reflecting the limited amount of sequence data available in the 1970s) almost certainly inflated the variance of some rate matrix parameters (alternatively, the proteins used to generate the PAM model could have been a non-representative set). Regardless, it is clear that the PAM model seldom has as good of a fit to most datasets as more modern empirical models (Keane et al. 2006 tested thousands of vertebrate, bacterial, and archaeal proteins and they found that the Dayhoff PAM model had the best-fit to at most <4% of the proteins).
Starting in the 1990s, the rapid expansion of sequence databases due to improved sequencing technologies led to the estimation of many new empirical matrices (see for a complete list). The earliest efforts used methods similar to those used by Dayhoff, using large-scale matching of the protein database to generate a new log-odds matrix and the JTT (Jones-Taylor-Thornton) model. The rapid increases in compute power during this time (reflecting factors such as Moore's law) made it feasible to estimate parameters for empirical models using maximum likelihood (e.g., the WAG and LG models) and other methods (e.g., the VT and PMB models). The IQ-Tree software package allows users to infer their own time reversible model using QMaker, or non-time-reversible using nQMaker.
The no common mechanism (NCM) model and maximum parsimony
In 1997, Tuffley and Steel described a model that they named the no common mechanism (NCM) model. The topology of the maximum likelihood tree for a specific dataset given the NCM model is identical to the topology of the optimal tree for the same data given the maximum parsimony criterion. The NCM model assumes all of the data (e.g., homologous nucleotides, amino acids, or morphological characters) are related by a common phylogenetic tree. Then parameters are introduced for each homologous character, where is the number of sequences. This can be viewed as estimating a separate rate parameter for every character × branch pair in the dataset (note that the number of branches in a fully resolved phylogenetic tree is ). Thus, the number of free parameters in the NCM model always exceeds the number of homologous characters in the data matrix, and the NCM model has been criticized as consistently "over-parameterized."
References
- ^ Steel M, Penny D (June 2000). "Parsimony, likelihood, and the role of models in molecular phylogenetics". Molecular Biology and Evolution. 17 (6): 839–850. doi:10.1093/oxfordjournals.molbev.a026364. PMID 10833190.
- Bromham L (May 2019). "Six Impossible Things before Breakfast: Assumptions, Models, and Belief in Molecular Dating". Trends in Ecology & Evolution. 34 (5): 474–486. doi:10.1016/j.tree.2019.01.017. PMID 30904189. S2CID 85496215.
- Yang Z, Bielawski JP (December 2000). "Statistical methods for detecting molecular adaptation". Trends in Ecology & Evolution. 15 (12): 496–503. doi:10.1016/s0169-5347(00)01994-7. PMC 7134603. PMID 11114436.
- Perron U, Kozlov AM, Stamatakis A, Goldman N, Moal IH (September 2019). Pupko T (ed.). "Modeling Structural Constraints on Protein Evolution via Side-Chain Conformational States". Molecular Biology and Evolution. 36 (9): 2086–2103. doi:10.1093/molbev/msz122. PMC 6736381. PMID 31114882.
- ^ Jukes TH, Cantor CH (1969). "Evolution of Protein Molecules". In Munro HN (ed.). Mammalian Protein Metabolism. Vol. 3. Elsevier. pp. 21–132. doi:10.1016/b978-1-4832-3211-9.50009-7. ISBN 978-1-4832-3211-9.
- Huelsenbeck JP, Hillis DM (1993-09-01). "Success of Phylogenetic Methods in the Four-Taxon Case". Systematic Biology. 42 (3): 247–264. doi:10.1093/sysbio/42.3.247. ISSN 1063-5157.
- Goldman N (February 1993). "Statistical tests of models of DNA substitution". Journal of Molecular Evolution. 36 (2): 182–198. Bibcode:1993JMolE..36..182G. doi:10.1007/BF00166252. PMID 7679448. S2CID 29354147.
- Swofford D.L. Olsen G.J. Waddell P.J. Hillis D.M. 1996. "Phylogenetic inference." in Molecular systematics (ed. Hillis D.M. Moritz C. Mable B.K.) 2nd ed. Sunderland, MA: Sinauer. p. 407–514. ISBN 978-0878932825
- Church SH, Ryan JF, Dunn CW (November 2015). "Automation and Evaluation of the SOWH Test with SOWHAT". Systematic Biology. 64 (6): 1048–1058. doi:10.1093/sysbio/syv055. PMC 4604836. PMID 26231182.
- Lewis PO (2001-11-01). "A likelihood approach to estimating phylogeny from discrete morphological character data". Systematic Biology. 50 (6): 913–925. doi:10.1080/106351501753462876. PMID 12116640.
- Lee MS, Cau A, Naish D, Dyke GJ (May 2014). "Morphological clocks in paleontology, and a mid-Cretaceous origin of crown Aves". Systematic Biology. 63 (3): 442–449. doi:10.1093/sysbio/syt110. PMID 24449041.
- Ronquist F, Klopfstein S, Vilhelmsen L, Schulmeister S, Murray DL, Rasnitsyn AP (December 2012). "A total-evidence approach to dating with fossils, applied to the early radiation of the hymenoptera". Systematic Biology. 61 (6): 973–999. doi:10.1093/sysbio/sys058. PMC 3478566. PMID 22723471.
- Brower, A. V .Z. (2016). "Are we all cladists?" in Williams, D., Schmitt, M., & Wheeler, Q. (Eds.). The future of phylogenetic systematics: The legacy of Willi Hennig (Systematics Association Special Volume Series Book 86). Cambridge University Press. pp. 88-114 ISBN 978-1107117648
- Farris JS, Kluge AG, Carpenter JM (June 2001). Olmstead R (ed.). "Popper and likelihood versus "Popper"". Systematic Biology. 50 (3): 438–444. doi:10.1080/10635150119150. PMID 12116585.
- Goldman, Nick (December 1990). "Maximum Likelihood Inference of Phylogenetic Trees, with Special Reference to a Poisson Process Model of DNA Substitution and to Parsimony Analyses". Systematic Zoology. 39 (4): 345–361. doi:10.2307/2992355. JSTOR 2992355.
- Gu X, Li WH (September 1992). "Higher rates of amino acid substitution in rodents than in humans". Molecular Phylogenetics and Evolution. 1 (3): 211–214. doi:10.1016/1055-7903(92)90017-B. PMID 1342937.
- Li WH, Ellsworth DL, Krushkal J, Chang BH, Hewett-Emmett D (February 1996). "Rates of nucleotide substitution in primates and rodents and the generation-time effect hypothesis". Molecular Phylogenetics and Evolution. 5 (1): 182–187. doi:10.1006/mpev.1996.0012. PMID 8673286.
- Martin AP, Palumbi SR (May 1993). "Body size, metabolic rate, generation time, and the molecular clock". Proceedings of the National Academy of Sciences of the United States of America. 90 (9): 4087–4091. Bibcode:1993PNAS...90.4087M. doi:10.1073/pnas.90.9.4087. PMC 46451. PMID 8483925.
- Yang Z, Nielsen R (April 1998). "Synonymous and nonsynonymous rate variation in nuclear genes of mammals". Journal of Molecular Evolution. 46 (4): 409–418. Bibcode:1998JMolE..46..409Y. CiteSeerX 10.1.1.19.7744. doi:10.1007/PL00006320. PMID 9541535. S2CID 13917969.
- Kishino H, Thorne JL, Bruno WJ (March 2001). "Performance of a divergence time estimation method under a probabilistic model of rate evolution". Molecular Biology and Evolution. 18 (3): 352–361. doi:10.1093/oxfordjournals.molbev.a003811. PMID 11230536.
- Thorne JL, Kishino H, Painter IS (December 1998). "Estimating the rate of evolution of the rate of molecular evolution". Molecular Biology and Evolution. 15 (12): 1647–1657. doi:10.1093/oxfordjournals.molbev.a025892. PMID 9866200.
- ^ Tavaré S. "Some Probabilistic and Statistical Problems in the Analysis of DNA Sequences" (PDF). Lectures on Mathematics in the Life Sciences. 17: 57–86.
- ^ Yang Z (2006). Computational molecular evolution. Oxford: Oxford University Press. ISBN 978-1-4294-5951-8. OCLC 99664975.
- ^ Yang Z (July 1994). "Estimating the pattern of nucleotide substitution". Journal of Molecular Evolution. 39 (1): 105–111. Bibcode:1994JMolE..39..105Y. doi:10.1007/BF00178256. PMID 8064867. S2CID 15895455.
- Swofford, D.L., Olsen, G.J., Waddell, P.J. and Hillis, D.M. (1996) Phylogenetic Inference. In: Hillis, D.M., Moritz, C. and Mable, B.K., Eds., Molecular Systematics, 2nd Edition, Sinauer Associates, Sunderland (MA), 407-514. ISBN 0878932828 ISBN 978-0878932825
- Felsenstein J (2004). Inferring phylogenies. Sunderland, Mass.: Sinauer Associates. ISBN 0-87893-177-5. OCLC 52127769.
- Swofford DL, Bell CD (1997). "(Draft) PAUP* manual". Retrieved 31 December 2019.
- ^ Felsenstein J (November 1981). "Evolutionary trees from DNA sequences: a maximum likelihood approach". Journal of Molecular Evolution. 17 (6): 368–376. Bibcode:1981JMolE..17..368F. doi:10.1007/BF01734359. PMID 7288891. S2CID 8024924.
- ^ Kimura M (December 1980). "A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences". Journal of Molecular Evolution. 16 (2): 111–120. Bibcode:1980JMolE..16..111K. doi:10.1007/BF01731581. PMID 7463489. S2CID 19528200.
- ^ Hasegawa M, Kishino H, Yano T (October 1985). "Dating of the human-ape splitting by a molecular clock of mitochondrial DNA". Journal of Molecular Evolution. 22 (2): 160–174. Bibcode:1985JMolE..22..160H. doi:10.1007/BF02101694. PMID 3934395. S2CID 25554168.
- ^ Kimura M (January 1981). "Estimation of evolutionary distances between homologous nucleotide sequences". Proceedings of the National Academy of Sciences of the United States of America. 78 (1): 454–458. Bibcode:1981PNAS...78..454K. doi:10.1073/pnas.78.1.454. PMC 319072. PMID 6165991.
- ^ Tamura K, Nei M (May 1993). "Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees". Molecular Biology and Evolution. 10 (3): 512–526. doi:10.1093/oxfordjournals.molbev.a040023. PMID 8336541.
- ^ Zharkikh A (September 1994). "Estimation of evolutionary distances between nucleotide sequences". Journal of Molecular Evolution. 39 (3): 315–329. Bibcode:1994JMolE..39..315Z. doi:10.1007/BF00160155. PMID 7932793. S2CID 33845318.
- Huelsenbeck JP, Larget B, Alfaro ME (June 2004). "Bayesian phylogenetic model selection using reversible jump Markov chain Monte Carlo". Molecular Biology and Evolution. 21 (6): 1123–1133. doi:10.1093/molbev/msh123. PMID 15034130.
- Yap VB, Pachter L (April 2004). "Identification of evolutionary hotspots in the rodent genomes". Genome Research. 14 (4): 574–579. doi:10.1101/gr.1967904. PMC 383301. PMID 15059998.
- Susko E, Roger AJ (September 2007). "On reduced amino acid alphabets for phylogenetic inference". Molecular Biology and Evolution. 24 (9): 2139–2150. doi:10.1093/molbev/msm144. PMID 17652333.
- Arbiza, Leonardo; Patricio, Mateus; Dopazo, Hernán; Posada, David (2011-01-01). "Genome-Wide Heterogeneity of Nucleotide Substitution Model Fit". Genome Biology and Evolution. 3: 896–908. doi:10.1093/gbe/evr080. ISSN 1759-6653. PMC 3175760. PMID 21824869.
- Halpern, A. L.; Bruno, W. J. (1998-07-01). "Evolutionary distances for protein-coding sequences: modeling site- specific residue frequencies". Molecular Biology and Evolution. 15 (7): 910–917. doi:10.1093/oxfordjournals.molbev.a025995. ISSN 0737-4038. PMID 9656490.
- Ponciano JM, Burleigh JG, Braun EL, Taper ML (December 2012). "Assessing parameter identifiability in phylogenetic models using data cloning". Systematic Biology. 61 (6): 955–972. doi:10.1093/sysbio/sys055. PMC 3478565. PMID 22649181.
- ^ Whelan S, Goldman N (May 2001). "A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach". Molecular Biology and Evolution. 18 (5): 691–699. doi:10.1093/oxfordjournals.molbev.a003851. PMID 11319253.
- Braun EL (July 2018). "An evolutionary model motivated by physicochemical properties of amino acids reveals variation among proteins". Bioinformatics. 34 (13): i350 – i356. doi:10.1093/bioinformatics/bty261. PMC 6022633. PMID 29950007.
- Goldman N, Whelan S (November 2002). "A novel use of equilibrium frequencies in models of sequence evolution". Molecular Biology and Evolution. 19 (11): 1821–1831. doi:10.1093/oxfordjournals.molbev.a004007. PMID 12411592.
- Kosiol C, Holmes I, Goldman N (July 2007). "An empirical codon model for protein sequence evolution". Molecular Biology and Evolution. 24 (7): 1464–1479. doi:10.1093/molbev/msm064. PMID 17400572.
- Tamura K (July 1992). "Estimation of the number of nucleotide substitutions when there are strong transition-transversion and G+C-content biases". Molecular Biology and Evolution. 9 (4): 678–687. doi:10.1093/oxfordjournals.molbev.a040752. PMID 1630306.
- Halpern AL, Bruno WJ (July 1998). "Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies". Molecular Biology and Evolution. 15 (7): 910–917. doi:10.1093/oxfordjournals.molbev.a025995. PMID 9656490. S2CID 7332698.
- ^ Braun EL, Kimball RT (August 2002). Kjer K (ed.). "Examining Basal avian divergences with mitochondrial sequences: model complexity, taxon sampling, and sequence length". Systematic Biology. 51 (4): 614–625. doi:10.1080/10635150290102294. PMID 12228003.
- Phillips MJ, Delsuc F, Penny D (July 2004). "Genome-scale phylogeny and the detection of systematic biases". Molecular Biology and Evolution. 21 (7): 1455–1458. doi:10.1093/molbev/msh137. PMID 15084674.
- Ishikawa SA, Inagaki Y, Hashimoto T (January 2012). "RY-Coding and Non-Homogeneous Models Can Ameliorate the Maximum-Likelihood Inferences From Nucleotide Sequence Data with Parallel Compositional Heterogeneity". Evolutionary Bioinformatics Online. 8: 357–371. doi:10.4137/EBO.S9017. PMC 3394461. PMID 22798721.
- Simmons MP, Ochoterena H (June 2000). "Gaps as characters in sequence-based phylogenetic analyses". Systematic Biology. 49 (2): 369–381. doi:10.1093/sysbio/49.2.369. PMID 12118412.
- Yuri T, Kimball RT, Harshman J, Bowie RC, Braun MJ, Chojnowski JL, et al. (March 2013). "Parsimony and model-based analyses of indels in avian nuclear genes reveal congruent and incongruent phylogenetic signals". Biology. 2 (1): 419–444. doi:10.3390/biology2010419. PMC 4009869. PMID 24832669.
- Houde P, Braun EL, Narula N, Minjares U, Mirarab S (2019-07-06). "Phylogenetic Signal of Indels and the Neoavian Radiation". Diversity. 11 (7): 108. doi:10.3390/d11070108.
- Cavender JA (August 1978). "Taxonomy with confidence". Mathematical Biosciences. 40 (3–4): 271–280. doi:10.1016/0025-5564(78)90089-5.
- Farris JS (1973-09-01). "A Probability Model for Inferring Evolutionary Trees". Systematic Biology. 22 (3): 250–256. doi:10.1093/sysbio/22.3.250. ISSN 1063-5157.
- Neyman J (1971). Gupta SS, Yackel J (eds.). Molecular Studies of Evolution: A Source of Novel Statistical Problems. New York, NY, USA: New York Academic Press. pp. 1–27.
- Waddell PJ, Penny D, Moore T (August 1997). "Hadamard conjugations and modeling sequence evolution with unequal rates across sites". Molecular Phylogenetics and Evolution. 8 (1): 33–50. doi:10.1006/mpev.1997.0405. PMID 9242594.
- Dayhoff MO, Eck RV, Park CM (1969). "A model of evolutionary change in proteins". In Dayhoff MO (ed.). Atlas of Protein Sequence and Structure. Vol. 4. pp. 75–84.
- Dayhoff MO, Schwartz RM, Orcutt BC (1978). "A model of evolutionary change in proteins" (PDF). In Dayhoff MO (ed.). Atlas of Protein Sequence and Structure. Vol. 5. pp. 345–352.
- Henikoff S, Henikoff JG (November 1992). "Amino acid substitution matrices from protein blocks". Proceedings of the National Academy of Sciences of the United States of America. 89 (22): 10915–10919. Bibcode:1992PNAS...8910915H. doi:10.1073/pnas.89.22.10915. PMC 50453. PMID 1438297.
- Altschul SF (March 1993). "A protein alignment scoring system sensitive at all evolutionary distances". Journal of Molecular Evolution. 36 (3): 290–300. Bibcode:1993JMolE..36..290A. doi:10.1007/BF00160485. PMID 8483166. S2CID 22532856.
- Kishino H, Miyata T, Hasegawa M (August 1990). "Maximum likelihood inference of protein phylogeny and the origin of chloroplasts". Journal of Molecular Evolution. 31 (2): 151–160. Bibcode:1990JMolE..31..151K. doi:10.1007/BF02109483. S2CID 24650412.
- Kosiol C, Goldman N (February 2005). "Different versions of the Dayhoff rate matrix". Molecular Biology and Evolution. 22 (2): 193–199. doi:10.1093/molbev/msi005. PMID 15483331.
- Keane TM, Creevey CJ, Pentony MM, Naughton TJ, Mclnerney JO (March 2006). "Assessment of methods for amino acid matrix selection and their use on empirical data shows that ad hoc assumptions for choice of matrix are not justified". BMC Evolutionary Biology. 6 (1): 29. Bibcode:2006BMCEE...6...29K. doi:10.1186/1471-2148-6-29. PMC 1435933. PMID 16563161.
- Bigot T, Guglielmini J, Criscuolo A (August 2019). "Simulation data for the estimation of numerical constants for approximating pairwise evolutionary distances between amino acid sequences". Data in Brief. 25: 104212. Bibcode:2019DIB....2504212B. doi:10.1016/j.dib.2019.104212. PMC 6699465. PMID 31440543.
- Gonnet GH, Cohen MA, Benner SA (June 1992). "Exhaustive matching of the entire protein sequence database". Science. 256 (5062): 1443–1445. Bibcode:1992Sci...256.1443G. doi:10.1126/science.1604319. PMID 1604319.
- Jones DT, Taylor WR, Thornton JM (June 1992). "The rapid generation of mutation data matrices from protein sequences". Computer Applications in the Biosciences. 8 (3): 275–282. doi:10.1093/bioinformatics/8.3.275. PMID 1633570.
- Le SQ, Gascuel O (July 2008). "An improved general amino acid replacement matrix". Molecular Biology and Evolution. 25 (7): 1307–1320. doi:10.1093/molbev/msn067. PMID 18367465.
- Müller T, Vingron M (December 2000). "Modeling amino acid replacement". Journal of Computational Biology. 7 (6): 761–776. doi:10.1089/10665270050514918. PMID 11382360.
- Veerassamy S, Smith A, Tillier ER (December 2003). "A transition probability model for amino acid substitutions from blocks". Journal of Computational Biology. 10 (6): 997–1010. doi:10.1089/106652703322756195. PMID 14980022.
- Minh, Bui Quang; Dang, Cuong Cao; Vinh, Le Sy; Lanfear, Robert (11 August 2021). "QMaker: Fast and Accurate Method to Estimate Empirical Models of Protein Evolution". Systematic Biology. 70 (5): 1046–1060. doi:10.1093/sysbio/syab010. PMC 8357343. PMID 33616668.
- Dang, Cuong Cao; Minh, Bui Quang; McShea, Hanon; Masel, Joanna; James, Jennifer Eleanor; Vinh, Le Sy; Lanfear, Robert (9 February 2022). "nQMaker: Estimating Time Nonreversible Amino Acid Substitution Models". Systematic Biology. 71 (5): 1110–1123. doi:10.1093/sysbio/syac007. PMC 9366462. PMID 35139203.
- Tuffley C, Steel M (May 1997). "Links between maximum likelihood and maximum parsimony under a simple model of site substitution". Bulletin of Mathematical Biology. 59 (3): 581–607. doi:10.1007/bf02459467. PMID 9172826. S2CID 189885872.
- Holder MT, Lewis PO, Swofford DL (July 2010). "The akaike information criterion will not choose the no common mechanism model". Systematic Biology. 59 (4): 477–485. doi:10.1093/sysbio/syq028. hdl:1808/9209. PMID 20547783.
A good model for phylogenetic inference must be rich enough to deal with sources of noise in the data, but ML estimation conducted using models that are clearly overparameterized can lead to drastically wrong conclusions. The NCM model certainly falls in the realm of being too parameter rich to serve as a justification of the use of parsimony based on it being an ML estimator under a general model.
External links
Notes
- The link describes the #ParsimonyGate controversy, which provides a concrete example of the debate regarding the philosophical nature of the maximum parsimony criterion. #ParsimonyGate was the reaction on Twitter to an editorial in the journal Cladistics, published by the Willi Hennig Society. The editorial states that the "...epistemological paradigm of this journal is parsimony" and stating that there are philosophical reasons to prefer parsimony to other methods of phylogenetic inference. Since other methods (i.e., maximum likelihood, Bayesian inference, phylogenetic invariants, and most distance methods) of phylogenetic inference are model-based this statement implicitly rejects the notion that parsimony is a model.


 for i ≠ j is the rate at which base i goes to base j. The diagonals of the Q matrix are chosen so that the rows sum to zero:
for i ≠ j is the rate at which base i goes to base j. The diagonals of the Q matrix are chosen so that the rows sum to zero:


 . The entry in the i column and the j row,
. The entry in the i column and the j row,  , is the probability, after time t, that there is a base j at a given position, conditional on there being a base i in that position at time 0. When the model is time reversible, this can be performed between any two sequences, even if one is not the ancestor of the other, if you know the total branch length between them.
, is the probability, after time t, that there is a base j at a given position, conditional on there being a base i in that position at time 0. When the model is time reversible, this can be performed between any two sequences, even if one is not the ancestor of the other, if you know the total branch length between them.
 or, in other words, as time goes to infinity the probability of finding base j at a position given there was a base i at that position originally goes to the equilibrium probability that there is base j at that position, regardless of the original base. Furthermore, it follows that
or, in other words, as time goes to infinity the probability of finding base j at a position given there was a base i at that position originally goes to the equilibrium probability that there is base j at that position, regardless of the original base. Furthermore, it follows that  for all t.
for all t.


 are the eigenvalues of Q, each repeated according to its multiplicity. Then
are the eigenvalues of Q, each repeated according to its multiplicity. Then


 , giving the frequency at which each base occurs at each site, and the rate matrix
, giving the frequency at which each base occurs at each site, and the rate matrix

 , the overall number of substitutions per unit time. When measuring time in substitutions (
, the overall number of substitutions per unit time. When measuring time in substitutions ( , and then add n-1 for the equilibrium frequencies, and subtract 1 because
, and then add n-1 for the equilibrium frequencies, and subtract 1 because 
 codons, resulting in 2078 free parameters. However, the rates for transitions between codons which differ by more than one base are often assumed to be zero, reducing the number of free parameters to only
codons, resulting in 2078 free parameters. However, the rates for transitions between codons which differ by more than one base are often assumed to be zero, reducing the number of free parameters to only  parameters. Another common practice is to reduce the number of codons by forbidding the stop (or
parameters. Another common practice is to reduce the number of codons by forbidding the stop (or  after time
after time  given that the ancestral codon is
given that the ancestral codon is  would involve the possibility of passing through a state with a premature stop codon.
would involve the possibility of passing through a state with a premature stop codon.
 matrix) for the nucleotide GTR model is:
matrix) for the nucleotide GTR model is:

 .
.
 through
through  , which can also be written using the notation
, which can also be written using the notation  ) or to equilibrium
) or to equilibrium  . Note that the nucleotides in the
. Note that the nucleotides in the 
 , where
, where  is the equilibrium frequency of the
is the equilibrium frequency of the  nucleotide. The matrix shown above uses the letters
nucleotide. The matrix shown above uses the letters  ,
,  , and so forth).
, and so forth).
 ) but the transition probability matrix values are not (i.e.,
) but the transition probability matrix values are not (i.e.,  is the probability of observing A in sequence 1 and C in sequence 2 when the evolutionary distance between those sequences is
is the probability of observing A in sequence 1 and C in sequence 2 when the evolutionary distance between those sequences is  is the probability of observing C in sequence 1 and A in sequence 2 at the same evolutionary distance).
is the probability of observing C in sequence 1 and A in sequence 2 at the same evolutionary distance).
 ) is typically set to a value of 1 to increase the readability of the exchangeability parameter estimates (since it allows users to express those values relative to chosen exchangeability parameter). The practice of expressing the exchangeability parameters in relative terms is not problematic because the
) is typically set to a value of 1 to increase the readability of the exchangeability parameter estimates (since it allows users to express those values relative to chosen exchangeability parameter). The practice of expressing the exchangeability parameters in relative terms is not problematic because the  to be expressed in units of expected substitutions per site (standard practice in molecular phylogenetics). This is the equivalent to the statement that one is setting the mutation rate
to be expressed in units of expected substitutions per site (standard practice in molecular phylogenetics). This is the equivalent to the statement that one is setting the mutation rate  , which are expressed relative to the fixed
, which are expressed relative to the fixed  in this example) and three equilibrium base frequency parameters (as described above, only three
in this example) and three equilibrium base frequency parameters (as described above, only three  values need to be specified because
values need to be specified because  must sum to 1).
must sum to 1).


 (
( (
( (
(
 (
(
 (
(

 and
and  but allowing
but allowing  ).
).
 ,
,  , ...
, ...  and a set of exchangeability parameters (
and a set of exchangeability parameters ( character states. These values can then be used to populate the
character states. These values can then be used to populate the  ), setting the diagonal elements
), setting the diagonal elements  to the negative sum of the off-diagonal elements on the same row, and normalizing. Obviously,
to the negative sum of the off-diagonal elements on the same row, and normalizing. Obviously,  for
for  for
for  and encode amino acids by recoding the amino acids using the six categories proposed by
and encode amino acids by recoding the amino acids using the six categories proposed by  (using the
(using the  and
and  , designated
, designated  and
and  , designated
, designated  parameters are introduced for each homologous character, where
parameters are introduced for each homologous character, where  is the number of sequences. This can be viewed as estimating a separate rate parameter for every character × branch pair in the dataset (note that the number of branches in a fully resolved phylogenetic tree is
is the number of sequences. This can be viewed as estimating a separate rate parameter for every character × branch pair in the dataset (note that the number of branches in a fully resolved phylogenetic tree is