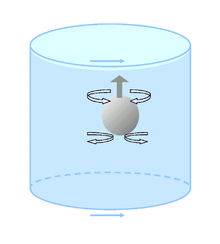
A Taylor column is a fluid dynamics phenomenon that occurs as a result of the Coriolis effect. It was named after Geoffrey Ingram Taylor. Rotating fluids that are perturbed by a solid body tend to form columns parallel to the axis of rotation called Taylor columns.
An object moving parallel to the axis of rotation in a rotating fluid experiences more drag force than what it would experience in a non rotating fluid. For example, a strongly buoyant ball (such as a pingpong ball) will rise to the surface more slowly than it would in a non-rotating fluid. This is because fluid in the path of the ball that is pushed out of the way tends to circulate back to the point it is shifted away from, due to the Coriolis effect. The faster the rotation rate, the smaller the radius of the inertial circle traveled by the fluid.
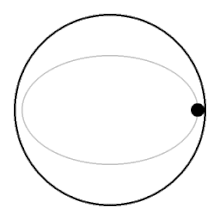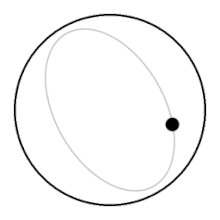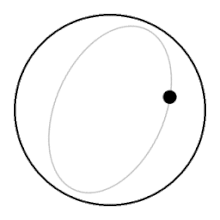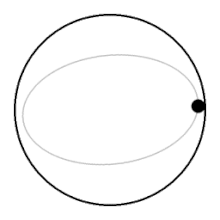
In a non-rotating fluid the fluid parts above the rising ball and closes in underneath it, offering relatively little resistance to the ball. In a rotating fluid, the ball needs to push up a whole column of fluid above it, and it needs to drag a whole column of fluid along beneath it in order to rise to the surface.
A rotating fluid thus displays some degree of rigidity.
History
Taylor columns were first observed by William Thomson, Lord Kelvin, in 1868. Taylor columns were featured in lecture demonstrations by Kelvin in 1881 and by John Perry in 1890. The phenomenon is explained via the Taylor–Proudman theorem, and it has been investigated by Taylor, Grace, Stewartson, and Maxworthy—among others.
Theory

Taylor columns have been rigorously studied. For Re<<1, Ek<<1, Ro<<1, the drag equation for a cylinder of radius, a, the following relation has been found.
To derive this, Moore and Saffman solved the linearised Navier–Stokes equation along in cylindrical coordinates, where some of the vertical and radial components of the viscous term are taken to be small relative to the Coriolis term:
To solve these equations, we incorporate the volume conservation condition as well:
We use the Ekman compatibility relation for this geometry to restrict the form of the velocity at the disk surface:
The resultant velocity fields can be solved in terms of Bessel functions.
whereby for Ek<<1 the function A(k) is given by,
Integrating the equation for the v, we can find the pressure and thus the drag force given by the first equation.
Geophysical example
Taylor columns form above peaks in the South Scotia Ridge in the Southern Ocean. They affect circulation and mixing in the Weddell-Scotia Confluence where the Antarctic circumpolar current (ACC) and the subpolar Weddell Gyre mix.
The iceberg A23a is approximately 50km across and broke free from the Antarctic coast in 1986. From July 2021 it tracked along the length of the Antarctic Peninsula, and in April 2024 it got stuck in one such Taylor Column in the ACC located over the Pirie Bank.
References
- James Thomson (Lord Kelvin's brother) (1868) Letter to William Thomson (30 September). Glasgow University Library, MS Kelvin T120.
- Velasco Fuentes, O. U. (2008). "Kelvin's discovery of Taylor columns" (PDF). European Journal of Mechanics. B / Fluids. 28 (3): 469–472. doi:10.1016/j.euromechflu.2008.11.002. Archived from the original (PDF) on 23 July 2011.
- Thomson, W. (1882) "Elasticity viewed as possibly a mode of motion," Proceedings of the Royal Institution, vol. 9, pages 520–521; also in: Popular Lectures and Addresses, vol. 1, pages 142–146. See also: Thomson, W. (1887) "On the stability of steady and of periodic fluid motion," Philosophical Magazine, vol. 23, pages 459–464. Also in: Mathematical and Physical Papers (Cambridge, England: Cambridge University Press, 1910), vol. 4, pp. 166-172.
- Perry, J. Spinning tops. The “Operatives’ lecture” of the British Association meeting at Leeds, 6th September, 1890. (London: Society for Promoting Christian Knowledge, 1910).
- Taylor, G.I. (1922) "The motion of a sphere in a rotating liquid," Proceedings of the Royal Society of London A, vol. 102, pages 180–189.
- Grace, S.F. (1922) "Free motion of a sphere in a rotating liquid parallel to the axis of rotation," Proceedings of the Royal Society of London A, vol. 102, pages 89–111.
- ^ Stewartson, K. (1952) "On the slow motion of a sphere along the axis of a rotating fluid," Proceedings of the Cambridge Philosophical Society, vol. 48, pages 168–177.
- Maxworthy, T. (1968) "The observed motion of a sphere through a short, rotating cylinder of fluid," Journal of Fluid Mechanics, vol. 31, pages 643–655. See also: Maxworthy, T. (1970) "The flow created by a sphere moving along the axis of a rotating, slightly-viscous fluid," Journal of Fluid Mechanics, vol. 40, pages 453–479.
- ^ Moore, D. W.; Saffman, P. G. (18 September 1969). "The Structure of Free Vertical Shear Layers in a Rotating Fluid and the Motion Produced by a Slowly Rising Body". Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 264 (1156): 597–634. Bibcode:1969RSPTA.264..597M. doi:10.1098/rsta.1969.0036. ISSN 1364-503X. S2CID 120026980.
- Meredith, M. P., A. S. Meijers, A. C. Naveira Garabato, P. J. Brown, H. J. Venables, E. P. Abrahamsen, L. Jullion, and M.-J. Messias (2015), Circulation, retention, and mixing of waters within the Weddell-Scotia Confluence, Southern Ocean: The role of stratified Taylor columns, J. Geophys. Res. Oceans, 120, 547–562, doi:10.1002/2014JC010462.
 This article incorporates text from this source, which is available under the CC BY 4.0 license.
This article incorporates text from this source, which is available under the CC BY 4.0 license.
- World's biggest iceberg spins in ocean trap, BBC News, 4 August 2024
Further reading
- Brenner, Michael P.; Stone, Howard A. (May 2000). "Modern Classical Physics Through the Work of G. I. Taylor". Physics Today. 53 (5): 30–35. Bibcode:2000PhT....53e..30B. doi:10.1063/1.883100.
External links
- Taylor columns (Martha Buckley, MIT)
- Record Player Fluid Dynamics: A Taylor Column Experiment (UCLA Spin Lab)









