In statistics, econometrics, epidemiology and related disciplines, the method of instrumental variables (IV) is used to estimate causal relationships when controlled experiments are not feasible or when a treatment is not successfully delivered to every unit in a randomized experiment. Intuitively, IVs are used when an explanatory variable of interest is correlated with the error term (endogenous), in which case ordinary least squares and ANOVA give biased results. A valid instrument induces changes in the explanatory variable (is correlated with the endogenous variable) but has no independent effect on the dependent variable and is not correlated with the error term, allowing a researcher to uncover the causal effect of the explanatory variable on the dependent variable.
Instrumental variable methods allow for consistent estimation when the explanatory variables (covariates) are correlated with the error terms in a regression model. Such correlation may occur when:
- changes in the dependent variable change the value of at least one of the covariates ("reverse" causation),
- there are omitted variables that affect both the dependent and explanatory variables, or
- the covariates are subject to measurement error.
Explanatory variables that suffer from one or more of these issues in the context of a regression are sometimes referred to as endogenous. In this situation, ordinary least squares produces biased and inconsistent estimates. However, if an instrument is available, consistent estimates may still be obtained. An instrument is a variable that does not itself belong in the explanatory equation but is correlated with the endogenous explanatory variables, conditionally on the value of other covariates.
In linear models, there are two main requirements for using IVs:
- The instrument must be correlated with the endogenous explanatory variables, conditionally on the other covariates. If this correlation is strong, then the instrument is said to have a strong first stage. A weak correlation may provide misleading inferences about parameter estimates and standard errors.
- The instrument cannot be correlated with the error term in the explanatory equation, conditionally on the other covariates. In other words, the instrument cannot suffer from the same problem as the original predicting variable. If this condition is met, then the instrument is said to satisfy the exclusion restriction.
Example
Informally, in attempting to estimate the causal effect of some variable X ("covariate" or "explanatory variable") on another Y ("dependent variable"), an instrument is a third variable Z which affects Y only through its effect on X.
For example, suppose a researcher wishes to estimate the causal effect of smoking (X) on general health (Y). Correlation between smoking and health does not imply that smoking causes poor health because other variables, such as depression, may affect both health and smoking, or because health may affect smoking. It is not possible to conduct controlled experiments on smoking status in the general population. The researcher may attempt to estimate the causal effect of smoking on health from observational data by using the tax rate for tobacco products (Z) as an instrument for smoking. The tax rate for tobacco products is a reasonable choice for an instrument because the researcher assumes that it can only be correlated with health through its effect on smoking. If the researcher then finds tobacco taxes and state of health to be correlated, this may be viewed as evidence that smoking causes changes in health.
History
The first use of an instrument variable occurred in a 1928 book by Philip G. Wright, best known for his excellent description of the production, transport and sale of vegetable and animal oils in the early 1900s in the United States. In 1945, Olav Reiersøl applied the same approach in the context of errors-in-variables models in his dissertation, giving the method its name.
Wright attempted to determine the supply and demand for butter using panel data on prices and quantities sold in the United States. The idea was that a regression analysis could produce a demand or supply curve because they are formed by the path between prices and quantities demanded or supplied. The problem was that the observational data did not form a demand or supply curve as such, but rather a cloud of point observations that took different shapes under varying market conditions. It seemed that making deductions from the data remained elusive.
The problem was that price affected both supply and demand so that a function describing only one of the two could not be constructed directly from the observational data. Wright correctly concluded that he needed a variable that correlated with either demand or supply but not both – that is, an instrumental variable.
After much deliberation, Wright decided to use regional rainfall as his instrumental variable: he concluded that rainfall affected grass production and hence milk production and ultimately butter supply, but not butter demand. In this way he was able to construct a regression equation with only the instrumental variable of price and supply.
Formal definitions of instrumental variables, using counterfactuals and graphical criteria, were given by Judea Pearl in 2000. Angrist and Krueger (2001) present a survey of the history and uses of instrumental variable techniques. Notions of causality in econometrics, and their relationship with instrumental variables and other methods, are discussed by Heckman (2008).
Theory
While the ideas behind IV extend to a broad class of models, a very common context for IV is in linear regression. Traditionally, an instrumental variable is defined as a variable that is correlated with the independent variable and uncorrelated with the "error term" U in the linear equation
is a vector. is a matrix, usually with a column of ones and perhaps with additional columns for other covariates. Consider how an instrument allows to be recovered. Recall that OLS solves for such that (when we minimize the sum of squared errors, , the first-order condition is exactly .) If the true model is believed to have due to any of the reasons listed above—for example, if there is an omitted variable which affects both and separately—then this OLS procedure will not yield the causal impact of on . OLS will simply pick the parameter that makes the resulting errors appear uncorrelated with .
Consider for simplicity the single-variable case. Suppose we are considering a regression with one variable and a constant (perhaps no other covariates are necessary, or perhaps we have partialed out any other relevant covariates):
In this case, the coefficient on the regressor of interest is given by . Substituting for gives
where is what the estimated coefficient vector would be if . In this case, it can be shown that is an unbiased estimator of . If in the underlying model that we believe, then OLS gives an inconsistent estimate which does not reflect the underlying causal effect of interest. IV helps to fix this problem by identifying the parameters not based on whether is uncorrelated with , but based on whether another variable is uncorrelated with . If theory suggests that is related to (the first stage) but uncorrelated with (the exclusion restriction), then IV may identify the causal parameter of interest where OLS fails. Because there are multiple specific ways of using and deriving IV estimators even in just the linear case (IV, 2SLS, GMM), we save further discussion for the Estimation section below.
Graphical definition
IV techniques have been developed among a much broader class of non-linear models. General definitions of instrumental variables, using counterfactual and graphical formalism, were given by Pearl (2000; p. 248). The graphical definition requires that Z satisfy the following conditions:
where stands for d-separation and stands for the graph in which all arrows entering X are cut off.
The counterfactual definition requires that Z satisfies
where Yx stands for the value that Y would attain had X been x and stands for independence.
If there are additional covariates W then the above definitions are modified so that Z qualifies as an instrument if the given criteria hold conditional on W.
The essence of Pearl's definition is:
- The equations of interest are "structural", not "regression".
- The error term U stands for all exogenous factors that affect Y when X is held constant.
- The instrument Z should be independent of U.
- The instrument Z should not affect Y when X is held constant (exclusion restriction).
- The instrument Z should not be independent of X.
These conditions do not rely on specific functional form of the equations and are applicable therefore to nonlinear equations, where U can be non-additive (see Non-parametric analysis). They are also applicable to a system of multiple equations, in which X (and other factors) affect Y through several intermediate variables. An instrumental variable need not be a cause of X; a proxy of such cause may also be used, if it satisfies conditions 1–5. The exclusion restriction (condition 4) is redundant; it follows from conditions 2 and 3.
Selecting suitable instruments
Since U is unobserved, the requirement that Z be independent of U cannot be inferred from data and must instead be determined from the model structure, i.e., the data-generating process. Causal graphs are a representation of this structure, and the graphical definition given above can be used to quickly determine whether a variable Z qualifies as an instrumental variable given a set of covariates W. To see how, consider the following example.
Suppose that we wish to estimate the effect of a university tutoring program on grade point average (GPA). The relationship between attending the tutoring program and GPA may be confounded by a number of factors. Students who attend the tutoring program may care more about their grades or may be struggling with their work. This confounding is depicted in the Figures 1–3 on the right through the bidirected arc between Tutoring Program and GPA. If students are assigned to dormitories at random, the proximity of the student's dorm to the tutoring program is a natural candidate for being an instrumental variable.
-
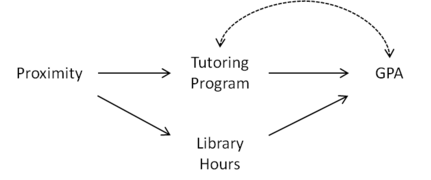 Figure 1: Proximity qualifies as an instrumental variable given Library Hours
Figure 1: Proximity qualifies as an instrumental variable given Library Hours
-
 Figure 2: , which is used to determine whether Proximity is an instrumental variable.
Figure 2: , which is used to determine whether Proximity is an instrumental variable.
-
 Figure 3: Proximity does not qualify as an instrumental variable given Library Hours
Figure 3: Proximity does not qualify as an instrumental variable given Library Hours
-
 Figure 4: Proximity qualifies as an instrumental variable, as long as we do not include Library Hours as a covariate.
Figure 4: Proximity qualifies as an instrumental variable, as long as we do not include Library Hours as a covariate.
However, what if the tutoring program is located in the college library? In that case, Proximity may also cause students to spend more time at the library, which in turn improves their GPA (see Figure 1). Using the causal graph depicted in the Figure 2, we see that Proximity does not qualify as an instrumental variable because it is connected to GPA through the path Proximity Library Hours GPA in . However, if we control for Library Hours by adding it as a covariate then Proximity becomes an instrumental variable, since Proximity is separated from GPA given Library Hours in .
Now, suppose that we notice that a student's "natural ability" affects his or her number of hours in the library as well as his or her GPA, as in Figure 3. Using the causal graph, we see that Library Hours is a collider and conditioning on it opens the path Proximity Library Hours GPA. As a result, Proximity cannot be used as an instrumental variable.
Finally, suppose that Library Hours does not actually affect GPA because students who do not study in the library simply study elsewhere, as in Figure 4. In this case, controlling for Library Hours still opens a spurious path from Proximity to GPA. However, if we do not control for Library Hours and remove it as a covariate then Proximity can again be used an instrumental variable.
Estimation
We now revisit and expand upon the mechanics of IV in greater detail. Suppose the data are generated by a process of the form
where
- i indexes observations,
- is the i-th value of the dependent variable,
- is a vector of the i-th values of the independent variable(s) and a constant,
- is the i-th value of an unobserved error term representing all causes of other than , and
- is an unobserved parameter vector.
The parameter vector is the causal effect on of a one unit change in each element of , holding all other causes of constant. The econometric goal is to estimate . For simplicity's sake assume the draws of e are uncorrelated and that they are drawn from distributions with the same variance (that is, that the errors are serially uncorrelated and homoskedastic).
Suppose also that a regression model of nominally the same form is proposed. Given a random sample of T observations from this process, the ordinary least squares estimator is
where X, y and e denote column vectors of length T. This equation is similar to the equation involving in the introduction (this is the matrix version of that equation). When X and e are uncorrelated, under certain regularity conditions the second term has an expected value conditional on X of zero and converges to zero in the limit, so the estimator is unbiased and consistent. When X and the other unmeasured, causal variables collapsed into the e term are correlated, however, the OLS estimator is generally biased and inconsistent for β. In this case, it is valid to use the estimates to predict values of y given values of X, but the estimate does not recover the causal effect of X on y.
To recover the underlying parameter , we introduce a set of variables Z that is highly correlated with each endogenous component of X but (in our underlying model) is not correlated with e. For simplicity, one might consider X to be a T × 2 matrix composed of a column of constants and one endogenous variable, and Z to be a T × 2 consisting of a column of constants and one instrumental variable. However, this technique generalizes to X being a matrix of a constant and, say, 5 endogenous variables, with Z being a matrix composed of a constant and 5 instruments. In the discussion that follows, we will assume that X is a T × K matrix and leave this value K unspecified. An estimator in which X and Z are both T × K matrices is referred to as just-identified .
Suppose that the relationship between each endogenous component xi and the instruments is given by
The most common IV specification uses the following estimator:
This specification approaches the true parameter as the sample gets large, so long as in the true model:
As long as in the underlying process which generates the data, the appropriate use of the IV estimator will identify this parameter. This works because IV solves for the unique parameter that satisfies , and therefore hones in on the true underlying parameter as the sample size grows.
Now an extension: suppose that there are more instruments than there are covariates in the equation of interest, so that Z is a T × M matrix with M > K. This is often called the over-identified case. In this case, the generalized method of moments (GMM) can be used. The GMM IV estimator is
where refers to the projection matrix .
This expression collapses to the first when the number of instruments is equal to the number of covariates in the equation of interest. The over-identified IV is therefore a generalization of the just-identified IV.
Proof that βGMM collapses to βIV in the just-identified caseDeveloping the expression:
In the just-identified case, we have as many instruments as covariates, so that the dimension of X is the same as that of Z. Hence, and are all squared matrices of the same dimension. We can expand the inverse, using the fact that, for any invertible n-by-n matrices A and B, (AB) = BA (see Invertible matrix#Properties):
Reference: see Davidson and Mackinnnon (1993)
There is an equivalent under-identified estimator for the case where m < k. Since the parameters are the solutions to a set of linear equations, an under-identified model using the set of equations does not have a unique solution.
Interpretation as two-stage least squares
One computational method which can be used to calculate IV estimates is two-stage least squares (2SLS or TSLS). In the first stage, each explanatory variable that is an endogenous covariate in the equation of interest is regressed on all of the exogenous variables in the model, including both exogenous covariates in the equation of interest and the excluded instruments. The predicted values from these regressions are obtained:
Stage 1: Regress each column of X on Z, ():
and save the predicted values:
In the second stage, the regression of interest is estimated as usual, except that in this stage each endogenous covariate is replaced with the predicted values from the first stage:
Stage 2: Regress Y on the predicted values from the first stage:
which gives
This method is only valid in linear models. For categorical endogenous covariates, one might be tempted to use a different first stage than ordinary least squares, such as a probit model for the first stage followed by OLS for the second. This is commonly known in the econometric literature as the forbidden regression, because second-stage IV parameter estimates are consistent only in special cases.
Proof: computation of the 2SLS estimatorThe usual OLS estimator is: . Replacing and noting that is a symmetric and idempotent matrix, so that
The resulting estimator of is numerically identical to the expression displayed above. A small correction must be made to the sum-of-squared residuals in the second-stage fitted model in order that the covariance matrix of is calculated correctly.
Non-parametric analysis
When the form of the structural equations is unknown, an instrumental variable can still be defined through the equations:
where and are two arbitrary functions and is independent of . Unlike linear models, however, measurements of and do not allow for the identification of the average causal effect of on , denoted ACE
Balke and Pearl derived tight bounds on ACE and showed that these can provide valuable information on the sign and size of ACE.
In linear analysis, there is no test to falsify the assumption the is instrumental relative to the pair . This is not the case when is discrete. Pearl (2000) has shown that, for all and , the following constraint, called "Instrumental Inequality" must hold whenever satisfies the two equations above:
Interpretation under treatment effect heterogeneity
The exposition above assumes that the causal effect of interest does not vary across observations, that is, that is a constant. Generally, different subjects will respond in different ways to changes in the "treatment" x. When this possibility is recognized, the average effect in the population of a change in x on y may differ from the effect in a given subpopulation. For example, the average effect of a job training program may substantially differ across the group of people who actually receive the training and the group which chooses not to receive training. For these reasons, IV methods invoke implicit assumptions on behavioral response, or more generally assumptions over the correlation between the response to treatment and propensity to receive treatment.
The standard IV estimator can recover local average treatment effects (LATE) rather than average treatment effects (ATE). Imbens and Angrist (1994) demonstrate that the linear IV estimate can be interpreted under weak conditions as a weighted average of local average treatment effects, where the weights depend on the elasticity of the endogenous regressor to changes in the instrumental variables. Roughly, that means that the effect of a variable is only revealed for the subpopulations affected by the observed changes in the instruments, and that subpopulations which respond most to changes in the instruments will have the largest effects on the magnitude of the IV estimate.
For example, if a researcher uses presence of a land-grant college as an instrument for college education in an earnings regression, she identifies the effect of college on earnings in the subpopulation which would obtain a college degree if a college is present but which would not obtain a degree if a college is not present. This empirical approach does not, without further assumptions, tell the researcher anything about the effect of college among people who would either always or never get a college degree regardless of whether a local college exists.
Weak instruments problem
As Bound, Jaeger, and Baker (1995) note, a problem is caused by the selection of "weak" instruments, instruments that are poor predictors of the endogenous question predictor in the first-stage equation. In this case, the prediction of the question predictor by the instrument will be poor and the predicted values will have very little variation. Consequently, they are unlikely to have much success in predicting the ultimate outcome when they are used to replace the question predictor in the second-stage equation.
In the context of the smoking and health example discussed above, tobacco taxes are weak instruments for smoking if smoking status is largely unresponsive to changes in taxes. If higher taxes do not induce people to quit smoking (or not start smoking), then variation in tax rates tells us nothing about the effect of smoking on health. If taxes affect health through channels other than through their effect on smoking, then the instruments are invalid and the instrumental variables approach may yield misleading results. For example, places and times with relatively health-conscious populations may both implement high tobacco taxes and exhibit better health even holding smoking rates constant, so we would observe a correlation between health and tobacco taxes even if it were the case that smoking has no effect on health. In this case, we would be mistaken to infer a causal effect of smoking on health from the observed correlation between tobacco taxes and health.
Testing for weak instruments
The strength of the instruments can be directly assessed because both the endogenous covariates and the instruments are observable. A common rule of thumb for models with one endogenous regressor is: the F-statistic against the null that the excluded instruments are irrelevant in the first-stage regression should be larger than 10.
Statistical inference and hypothesis testing
When the covariates are exogenous, the small-sample properties of the OLS estimator can be derived in a straightforward manner by calculating moments of the estimator conditional on X. When some of the covariates are endogenous so that instrumental variables estimation is implemented, simple expressions for the moments of the estimator cannot be so obtained. Generally, instrumental variables estimators only have desirable asymptotic, not finite sample, properties, and inference is based on asymptotic approximations to the sampling distribution of the estimator. Even when the instruments are uncorrelated with the error in the equation of interest and when the instruments are not weak, the finite sample properties of the instrumental variables estimator may be poor. For example, exactly identified models produce finite sample estimators with no moments, so the estimator can be said to be neither biased nor unbiased, the nominal size of test statistics may be substantially distorted, and the estimates may commonly be far away from the true value of the parameter.
Testing the exclusion restriction
The assumption that the instruments are not correlated with the error term in the equation of interest is not testable in exactly identified models. If the model is overidentified, there is information available which may be used to test this assumption. The most common test of these overidentifying restrictions, called the Sargan–Hansen test, is based on the observation that the residuals should be uncorrelated with the set of exogenous variables if the instruments are truly exogenous. The Sargan–Hansen test statistic can be calculated as (the number of observations multiplied by the coefficient of determination) from the OLS regression of the residuals onto the set of exogenous variables. This statistic will be asymptotically chi-squared with m − k degrees of freedom under the null that the error term is uncorrelated with the instruments.
See also
- Control function (econometrics) – Statistical methods to correct for endogeneity problems
- Optimal instruments – Technique for improving the efficiency of estimators in conditional moment models
References
- ^ Imbens, G.; Angrist, J. (1994). "Identification and estimation of local average treatment effects". Econometrica. 62 (2): 467–476. doi:10.2307/2951620. JSTOR 2951620. S2CID 153123153.
- Bullock, J. G.; Green, D. P.; Ha, S. E. (2010). "Yes, But What's the Mechanism? (Don't Expect an Easy Answer)". Journal of Personality and Social Psychology. 98 (4): 550–558. CiteSeerX 10.1.1.169.5465. doi:10.1037/a0018933. PMID 20307128. S2CID 7913867.
- https://www.stata.com/meeting/5nasug/wiv.pdf
- Nichols, Austin (2006-07-23). "Weak Instruments: An Overview and New Techniques".
{{cite journal}}: Cite journal requires|journal=(help) - Leigh, J. P.; Schembri, M. (2004). "Instrumental Variables Technique: Cigarette Price Provided Better Estimate of Effects of Smoking on SF-12". Journal of Clinical Epidemiology. 57 (3): 284–293. doi:10.1016/j.jclinepi.2003.08.006. PMID 15066689.
- Epstein, Roy J. (1989). "The Fall of OLS in Structural Estimation". Oxford Economic Papers. 41 (1): 94–107. doi:10.1093/oxfordjournals.oep.a041930. JSTOR 2663184.
- Stock, James H.; Trebbi, Francesco (2003). "Retrospectives: Who Invented Instrumental Variable Regression?". Journal of Economic Perspectives. 17 (3): 177–194. doi:10.1257/089533003769204416.
- Reiersøl, Olav (1945). Confluence Analysis by Means of Instrumental Sets of Variables. Arkiv for Mathematic, Astronomi, och Fysik. Vol. 32A. Uppsala: Almquist & Wiksells. OCLC 793451601.
- Wooldridge, J.: Introductory Econometrics. South-Western, Scarborough, Kanada, 2009.
- ^ Pearl, J. (2000). Causality: Models, Reasoning, and Inference. New York: Cambridge University Press. ISBN 978-0-521-89560-6.
- Angrist, J.; Krueger, A. (2001). "Instrumental Variables and the Search for Identification: From Supply and Demand to Natural Experiments". Journal of Economic Perspectives. 15 (4): 69–85. doi:10.1257/jep.15.4.69. hdl:1721.1/63775.
- Heckman, J. (2008). "Econometric Causality". International Statistical Review. 76 (1): 1–27. doi:10.1111/j.1751-5823.2007.00024.x.
- Bowden, R.J.; Turkington, D.A. (1984). Instrumental Variables. Cambridge, England: Cambridge University Press.
- Davidson, Russell; Mackinnon, James (1993). Estimation and Inference in Econometrics. New York: Oxford University Press. ISBN 978-0-19-506011-9.
- Wooldridge, J. (2010). Econometric Analysis of Cross Section and Panel Data. Econometric Analysis of Cross Section and Panel Data. MIT Press.
- Lergenmuller, Simon (2017). Two-stage predictor substitution for time-to-event data (Thesis). hdl:10852/57801.
- Balke, A.; Pearl, J. (1997). "Bounds on treatment effects from studies with imperfect compliance". Journal of the American Statistical Association. 92 (439): 1172–1176. CiteSeerX 10.1.1.26.3952. doi:10.1080/01621459.1997.10474074. S2CID 18365761.
- Heckman, J. (1997). "Instrumental variables: A study of implicit behavioral assumptions used in making program evaluations". Journal of Human Resources. 32 (3): 441–462. doi:10.2307/146178. JSTOR 146178.
- Bound, J.; Jaeger, D. A.; Baker, R. M. (1995). "Problems with Instrumental Variables Estimation when the Correlation between the Instruments and the Endogenous Explanatory Variable is Weak". Journal of the American Statistical Association. 90 (430): 443. doi:10.1080/01621459.1995.10476536.
- Stock, J.; Wright, J.; Yogo, M. (2002). "A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments". Journal of the American Statistical Association. 20 (4): 518–529. CiteSeerX 10.1.1.319.2477. doi:10.1198/073500102288618658. S2CID 14793271.
- Nelson, C. R.; Startz, R. (1990). "Some Further Results on the Exact Small Sample Properties of the Instrumental Variable Estimator". Econometrica. 58 (4): 967–976. doi:10.2307/2938359. JSTOR 2938359. S2CID 119872226.
- Hayashi, Fumio (2000). "Testing Overidentifying Restrictions". Econometrics. Princeton: Princeton University Press. pp. 217–221. ISBN 978-0-691-01018-2.
Further reading
- Greene, William H. (2008). Econometric Analysis (Sixth ed.). Upper Saddle River: Pearson Prentice-Hall. pp. 314–353. ISBN 978-0-13-600383-0.
- Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill Irwin. pp. 711–736. ISBN 978-0-07-337577-9.
- Keane, Michael P.; Neal, Timothy (2024). "A Practical Guide to Weak Instruments". Annual Review of Economics. 16: 185–212.
- Sargan, Denis (1988). Lectures on Advanced Econometric Theory. Oxford: Basil Blackwell. pp. 42–67. ISBN 978-0-631-14956-9.
- Wooldridge, Jeffrey M. (2013). Introductory Econometrics: A Modern Approach (Fifth international ed.). Mason, OH: South-Western. pp. 490–528. ISBN 978-1-111-53439-4.
Bibliography
- Wooldridge, J. (1997): Quasi-Likelihood Methods for Count Data, Handbook of Applied Econometrics, Volume 2, ed. M. H. Pesaran and P. Schmidt, Oxford, Blackwell, pp. 352–406
- Terza, J. V. (1998): "Estimating Count Models with Endogenous Switching: Sample Selection and Endogenous Treatment Effects." Journal of Econometrics (84), pp. 129–154
- Wooldridge, J. (2002): "Econometric Analysis of Cross Section and Panel Data", MIT Press, Cambridge, Massachusetts.
External links
- Chapter from Daniel McFadden's textbook
- Econometrics lecture (topic: instrumental variable) on YouTube by Mark Thoma.
- Econometrics lecture (topic: two-stages least square) on YouTube by Mark Thoma
 that is correlated with the independent variable
that is correlated with the independent variable
 and uncorrelated with the "error term" U in the linear equation
and uncorrelated with the "error term" U in the linear equation

 is a vector.
is a vector.  to be recovered. Recall that
to be recovered. Recall that  such that
such that  (when we minimize the sum of squared errors,
(when we minimize the sum of squared errors,  , the first-order condition is exactly
, the first-order condition is exactly  .) If the true model is believed to have
.) If the true model is believed to have  due to any of the reasons listed above—for example, if there is an
due to any of the reasons listed above—for example, if there is an 
 . Substituting for
. Substituting for  gives
gives

 is what the estimated coefficient vector would be if
is what the estimated coefficient vector would be if
 . In this case, it can be shown that
. In this case, it can be shown that  in the underlying model that we believe, then
in the underlying model that we believe, then  not based on whether
not based on whether  is uncorrelated with
is uncorrelated with  , but based on whether another variable
, but based on whether another variable  is uncorrelated with
is uncorrelated with 
 stands for
stands for  stands for the
stands for the 
 Library Hours
Library Hours  GPA. As a result, Proximity cannot be used as an instrumental variable.
GPA. As a result, Proximity cannot be used as an instrumental variable.

 is the i-th value of the dependent variable,
is the i-th value of the dependent variable, is a vector of the i-th values of the independent variable(s) and a constant,
is a vector of the i-th values of the independent variable(s) and a constant, is the i-th value of an unobserved error term representing all causes of
is the i-th value of an unobserved error term representing all causes of 
 in the introduction (this is the matrix version of that equation). When X and e are
in the introduction (this is the matrix version of that equation). When X and e are 

 in the true model:
in the true model:


 refers to the
refers to the  .
.
 expression:
expression:

 and
and  are all squared matrices of the same dimension. We can expand the inverse, using the fact that, for any invertible n-by-n matrices A and B, (AB) = BA (see
are all squared matrices of the same dimension. We can expand the inverse, using the fact that, for any invertible n-by-n matrices A and B, (AB) = BA (see 
 does not have a unique solution.
does not have a unique solution.
 ):
):




 .
Replacing
.
Replacing  and noting that
and noting that 



 and
and  are two arbitrary functions and
are two arbitrary functions and  . Unlike linear models, however, measurements of
. Unlike linear models, however, measurements of  and
and 
 . This is not the case when
. This is not the case when 
 (the number of observations multiplied by the
(the number of observations multiplied by the