| This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: "Virtual fixture" – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove this message) |
A virtual fixture is an overlay of augmented sensory information upon a user's perception of a real environment in order to improve human performance in both direct and remotely manipulated tasks. Developed in the early 1990s by Louis Rosenberg at the U.S. Air Force Research Laboratory (AFRL), Virtual Fixtures was a pioneering platform in virtual reality and augmented reality technologies.
History
Virtual Fixtures was first developed by Louis Rosenberg in 1992 at the USAF Armstrong Labs, resulting in the first immersive augmented reality system ever built. Because 3D graphics were too slow in the early 1990s to present a photorealistic and spatially-registered augmented reality, Virtual Fixtures used two real physical robots, controlled by a full upper-body exoskeleton worn by the user. To create the immersive experience for the user, a unique optics configuration was employed that involved a pair of binocular magnifiers aligned so that the user's view of the robot arms were brought forward so as to appear registered in the exact location of the user's real physical arms. The result was a spatially-registered immersive experience in which the user moved his or her arms, while seeing robot arms in the place where his or her arms should be. The system also employed computer-generated virtual overlays in the form of simulated physical barriers, fields, and guides, designed to assist in the user while performing real physical tasks.
Fitts Law performance testing was conducted on batteries of human test subjects, demonstrating for the first time, that a significant enhancement in human performance of real-world dexterous tasks could be achieved by providing immersive augmented reality overlays to users.
Concept

The concept of virtual fixtures was first introduced as an overlay of virtual sensory information on a workspace in order to improve human performance in direct and remotely manipulated tasks. The virtual sensory overlays can be presented as physically realistic structures, registered in space such that they are perceived by the user to be fully present in the real workspace environment. The virtual sensory overlays can also be abstractions that have properties not possible of real physical structures. The concept of sensory overlays is difficult to visualize and talk about, as a consequence the virtual fixture metaphor was introduced. To understand what a virtual fixture is an analogy with a real physical fixture such as a ruler is often used. A simple task such as drawing a straight line on a piece of paper free-hand is a task that most humans are unable to perform with good accuracy and high speed. However, the use of a simple device such as a ruler allows the task to be carried out quickly and with good accuracy. The use of a ruler helps the user by guiding the pen along the ruler reducing the tremor and mental load of the user, thus increasing the quality of the results.

When the Virtual Fixture concept was proposed to the U.S. Air Force in 1991, augmented surgery was an example use case, expanding the idea from a virtual ruler guiding a real pencil, to a virtual medical fixture guiding a real physical scalpel manipulated by a real surgeon. The objective was to overlay virtual content upon the surgeon's direct perception of the real workspace with sufficient realism that it would be perceived as authentic additions to the surgical environment and thereby enhance surgical skill, dexterity, and performance. A proposed benefit of virtual medical fixtures as compared to real hardware was that because they were virtual additions to the ambient reality, they could be partially submerged within real patients, providing guidance and/or barriers within unexposed tissues.
The definition of virtual fixtures is much broader than simply providing guidance of the end-effector. For example, auditory virtual fixtures are used to increase the user awareness by providing audio clues that helps the user by providing multi modal cues for localization of the end-effector. However, in the context of human-machine collaborative systems, the term virtual fixtures is often used to refer to a task dependent virtual aid that is overlaid upon a real environment and guides the user's motion along desired directions while preventing motion in undesired directions or regions of the workspace.
Virtual fixtures can be either guiding virtual fixtures or forbidden regions virtual fixtures. A forbidden regions virtual fixture could be used, for example, in a teleoperated setting where the operator has to drive a vehicle at a remote site to accomplish an objective. If there are pits at the remote site which would be harmful for the vehicle to fall into forbidden regions could be defined at the various pits locations, thus preventing the operator from issuing commands that would result in the vehicle ending up in such a pit.
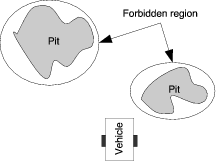
Such illegal commands could easily be sent by an operator because of, for instance, delays in the teleoperation loop, poor telepresence or a number of other reasons.
An example of a guiding virtual fixture could be when the vehicle must follow a certain trajectory,

The operator is then able to control the progress along the preferred direction while motion along the non-preferred direction is constrained.
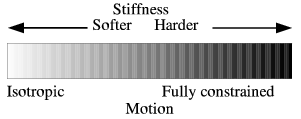
With both forbidden regions and guiding virtual fixtures the stiffness, or its inverse the compliance, of the fixture can be adjusted. If the compliance is high (low stiffness) the fixture is soft. On the other hand, when the compliance is zero (maximum stiffness) the fixture is hard.
Virtual fixture control law
This section describes how a control law that implements virtual fixtures can be derived. It is assumed that the robot is a purely kinematic device with end-effector position and end-effector orientation expressed in the robot's base frame . The input control signal to the robot is assumed to be a desired end-effector velocity . In a tele-operated system it is often useful to scale the input velocity from the operator, before feeding it to the robot controller. If the input from the user is of another form such as a force or position it must first be transformed to an input velocity, by for example scaling or differentiating.
Thus the control signal would be computed from the operator's input velocity as:
If there exists a one-to-one mapping between the operator and the slave robot.
If the constant is replaced by a diagonal matrix it is possible to adjust the compliance independently for different dimensions of . For example, setting the first three elements on the diagonal of to and all other elements to zero would result in a system that only permits translational motion and not rotation. This would be an example of a hard virtual fixture that constrains the motion from to . If the rest of the elements on the diagonal were set to a small value, instead of zero, the fixture would be soft, allowing some motion in the rotational directions.
To express more general constraints assume a time-varying matrix which represents the preferred direction at time . Thus if the preferred direction is along a curve in . Likewise, would give preferred directions that span a surface. From two projection operators can be defined, the span and kernel of the column space:
If does not have full column rank the span can not be computed, consequently it is better to compute the span by using the pseudo-inverse, thus in practice the span is computed as:
where denotes the pseudo-inverse of .
If the input velocity is split into two components as:
it is possible to rewrite the control law as:
Next introduce a new compliance that affects only the non-preferred component of the velocity input and write the final control law as:
References
- Rosenberg, Louis B. (2022). "Augmented Reality: Reflections at Thirty Years". In Arai, Kohei (ed.). Proceedings of the Future Technologies Conference (FTC) 2021, Volume 1. Lecture Notes in Networks and Systems. Vol. 358. Cham: Springer International Publishing. pp. 1–11. doi:10.1007/978-3-030-89906-6_1. ISBN 978-3-030-89906-6.
- ^ L. B. Rosenberg (1992). "The Use of Virtual Fixtures As Perceptual Overlays to Enhance Operator Performance in Remote Environments" (PDF). Technical Report AL-TR-0089. Wright-Patterson AFB OH: USAF Armstrong Laboratory. Archived (PDF) from the original on July 10, 2019.
- ^ Rosenberg, L.B. (1993). "Virtual fixtures: Perceptual tools for telerobotic manipulation". Proceedings of IEEE Virtual Reality Annual International Symposium. IEEE. pp. 76–82. doi:10.1109/vrais.1993.380795. ISBN 0-7803-1363-1.
- Rosenberg, Louis (1993). "The use of virtual fixtures to enhance telemanipulation with time delay". Proceedings of the ASME Winter Annual Meeting on Advances in Robotics, Mechatronics, and Haptic Interfaces. 49. New Orleans, LA: 29–36.
- ^ Rosenberg, Louis (1993). "The use of virtual fixtures to enhance operator performance in time delayed teleoperation" (PDF). J. Dyn. Syst. Control. 49: 29–36. Archived (PDF) from the original on July 10, 2019.
- Noer, Michael (1998-09-21). "Desktop fingerprints". Forbes. Retrieved 22 April 2014.
- ^ Rosenberg, L. (1993). Kim, Won S. (ed.). "Virtual fixtures as tools to enhance operator performance in telepresence environments". SPIE Manipulator Technology. Telemanipulator Technology and Space Telerobotics. 2057: 10. Bibcode:1993SPIE.2057...10R. doi:10.1117/12.164901. S2CID 111277519.
- Abbott, Jake J.; Marayong, Panadda; Okamura, Allison M. (2007). "Haptic Virtual Fixtures for Robot-Assisted Manipulation". In Thrun, Sebastian; Brooks, Rodney; Durrant-Whyte, Hugh (eds.). Robotics Research. Springer Tracts in Advanced Robotics. Vol. 28. Berlin, Heidelberg: Springer. pp. 49–64. doi:10.1007/978-3-540-48113-3_5. ISBN 978-3-540-48113-3.
- ^ Rosenberg (1994). Das, Hari (ed.). "Virtual Haptic Overlays Enhance Performance in Telepresence Tasks". Telemanipulator and Telepresence Technologies. 2351: 99–108. doi:10.1117/12.197302. S2CID 110971407.
- Makhataeva, Zhanat; Varol, Huseyin Atakan (2020). "Augmented Reality for Robotics: A Review". Robotics. 9 (2): 21. doi:10.3390/robotics9020021. ISSN 2218-6581.
- Leonard, Simon (2015). "Registration of planar virtual fixtures by using augmented reality with dynamic textures". 2015 IEEE International Conference on Robotics and Automation (ICRA). Seattle, WA, USA: IEEE. pp. 4418–4423. doi:10.1109/ICRA.2015.7139810. ISBN 978-1-4799-6923-4. S2CID 16744811.
- Xia, Tian; Léonard, Simon; Deguet, Anton; Whitcomb, Louis; Kazanzides, Peter (2012). "Augmented reality environment with virtual fixtures for robotic telemanipulation in space". 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. pp. 5059–5064. doi:10.1109/IROS.2012.6386169. ISBN 978-1-4673-1736-8. S2CID 2708501.
- Rosenberg, Louis B. (1993). Kim, Won S. (ed.). "Virtual fixtures as tools to enhance operator performance in telepresence environments". Telemanipulator Technology and Space Telerobotics. 2057: 10–21. Bibcode:1993SPIE.2057...10R. doi:10.1117/12.164901. S2CID 111277519.
- Rosenberg, L. B. (1992). "The Use of Virtual Fixtures as Perceptual Overlays to Enhance Operator Performance" Stanford University, Stanford CA, Center for Design Research (CDR)
- Yamamoto, Tomonori; Abolhassani, Niki; Jung, Sung; Okamura, Allison M.; Judkins, Timothy N. (2011-11-08). "Augmented reality and haptic interfaces for robot-assisted surgery". The International Journal of Medical Robotics and Computer Assisted Surgery. 8 (1): 45–56. doi:10.1002/rcs.421. ISSN 1478-5951. PMID 22069247. S2CID 1603125.
- Abbott, J.J.; Okamura, A.M. (2003). "Virtual fixture architectures for telemanipulation". 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422). Vol. 2. Taipei, Taiwan: IEEE. pp. 2798–2805. doi:10.1109/ROBOT.2003.1242016. ISBN 978-0-7803-7736-3. S2CID 8678829.
- Marayong, Panadda; Hager, Gregory D.; Okamura, Allison M. (2008). "Control methods for guidance virtual fixtures in compliant human-machine interfaces". 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. pp. 1166–1172. doi:10.1109/IROS.2008.4650838. ISBN 978-1-4244-2057-5. S2CID 6828466.
- Marayong, P.; Hager, G.D.; Okamura, A.M. (2006). "Effect of Hand Dynamics on Virtual Fixtures for Compliant Human-Machine Interfaces". 2006 14th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems. Alexandria, VA, USA: IEEE. pp. 109–115. doi:10.1109/HAPTIC.2006.1627075. ISBN 978-1-4244-0226-7.
- ^ Marayong, P.; Okamura, A.M.; Hager, G.D. (2003). "Spatial motion constraints: theory and demonstrations for robot guidance using virtual fixtures". 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422). IEEE. pp. 1270–1275. doi:10.1109/robot.2003.1241880. ISBN 0-7803-7736-2.
 and end-effector orientation
and end-effector orientation  expressed in the robot's base frame
expressed in the robot's base frame  . The input control signal
. The input control signal  to the robot is assumed to be a desired end-effector velocity
to the robot is assumed to be a desired end-effector velocity  . In a tele-operated system it is often useful to scale the input velocity from the operator,
. In a tele-operated system it is often useful to scale the input velocity from the operator,  before feeding it to the robot controller. If the input from the user is of another form such as a force or position it must first be transformed to an input velocity, by for example scaling or differentiating.
before feeding it to the robot controller. If the input from the user is of another form such as a force or position it must first be transformed to an input velocity, by for example scaling or differentiating.

 there exists a one-to-one mapping between the operator and the slave robot.
there exists a one-to-one mapping between the operator and the slave robot.
 is replaced by a diagonal matrix
is replaced by a diagonal matrix  it is possible to adjust the compliance independently for different dimensions of
it is possible to adjust the compliance independently for different dimensions of  . For example, setting the first three elements on the diagonal of
. For example, setting the first three elements on the diagonal of  to
to
 . If the rest of the elements on the diagonal were set to a small value, instead of zero, the fixture would be soft, allowing some motion in the rotational directions.
. If the rest of the elements on the diagonal were set to a small value, instead of zero, the fixture would be soft, allowing some motion in the rotational directions.
 which represents the preferred direction at time
which represents the preferred direction at time  . Thus if
. Thus if  the preferred direction is along a curve in
the preferred direction is along a curve in  . Likewise,
. Likewise,  would give preferred directions that span a surface. From
would give preferred directions that span a surface. From  two
projection operators can be defined, the span and kernel of the column space:
two
projection operators can be defined, the span and kernel of the column space:


 denotes the pseudo-inverse of
denotes the pseudo-inverse of 

