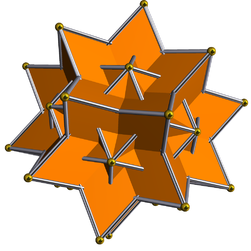
| Great rhombic triacontahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 30, E = 60 V = 32 (χ = 2) |
| Symmetry group | Ih, , *532 |
| Index references | DU54 |
| dual polyhedron | Great icosidodecahedron |

In geometry, the great rhombic triacontahedron is a nonconvex isohedral, isotoxal polyhedron. It is the dual of the great icosidodecahedron (U54). Like the convex rhombic triacontahedron it has 30 rhombic faces, 60 edges and 32 vertices (also 20 on 3-fold and 12 on 5-fold axes).
It can be constructed from the convex solid by expanding the faces by factor of , where is the golden ratio.
This solid is to the compound of great icosahedron and great stellated dodecahedron what the convex one is to the compound of dodecahedron and icosahedron: The crossing edges in the dual compound are the diagonals of the rhombs.
What resembles an "excavated" rhombic triacontahedron (compare excavated dodecahedron and excavated icosahedron) can be seen within the middle of this compound. The rest of the polyhedron strikingly resembles a rhombic hexecontahedron.
The rhombs have two angles of , and two of . Its dihedral angles equal . Part of each rhomb lies inside the solid, hence is invisible in solid models. The ratio between the lengths of the long and short diagonal of the rhombs equals the golden ratio .
      Convex, medial and great rhombic triacontahedron on the right (shown with pyritohedral symmetry) and the corresponding dual compounds of regular solids on the left Convex, medial and great rhombic triacontahedron on the right (shown with pyritohedral symmetry) and the corresponding dual compounds of regular solids on the left
|
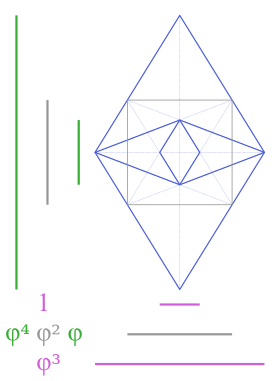 |
   Orthographic projections from 2-, 3- and 5-fold axes Orthographic projections from 2-, 3- and 5-fold axes
|
References
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
External links
- Weisstein, Eric W. "Great rhombic triacontahedron". MathWorld.
- David I. McCooey: animation and measurements
- Uniform polyhedra and duals
| Star-polyhedra navigator | |
|---|---|
| Kepler-Poinsot polyhedra (nonconvex regular polyhedra) | |
| Uniform truncations of Kepler-Poinsot polyhedra | |
| Nonconvex uniform hemipolyhedra | |
| Duals of nonconvex uniform polyhedra |
|
| Duals of nonconvex uniform polyhedra with infinite stellations | |
This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |
 , where
, where  is the
is the  , and two of
, and two of  . Its
. Its  . Part of each rhomb lies inside the solid, hence is invisible in solid models. The ratio between the lengths of the long and short diagonal of the rhombs equals the golden ratio
. Part of each rhomb lies inside the solid, hence is invisible in solid models. The ratio between the lengths of the long and short diagonal of the rhombs equals the golden ratio  .
.