 First iterations of the quadratic type 2 Koch curve, the Minkowski sausage
First iterations of the quadratic type 2 Koch curve, the Minkowski sausage Alternative generator with dimension of ln 18/ln 6 ≈ 1.61
Alternative generator with dimension of ln 18/ln 6 ≈ 1.61


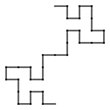 Generator
Generator island
island
The Minkowski sausage or Minkowski curve is a fractal first proposed by and named for Hermann Minkowski as well as its casual resemblance to a sausage or sausage links. The initiator is a line segment and the generator is a broken line of eight parts one fourth the length.
The Sausage has a Hausdorff dimension of . It is therefore often chosen when studying the physical properties of non-integer fractal objects. It is strictly self-similar. It never intersects itself. It is continuous everywhere, but differentiable nowhere. It is not rectifiable. It has a Lebesgue measure of 0. The type 1 curve has a dimension of ln 5/ln 3 ≈ 1.46.
Multiple Minkowski Sausages may be arranged in a four sided polygon or square to create a quadratic Koch island or Minkowski island/flake:
Islands Island formed by a different generator with a dimension of ≈1.36521 or 3/2
Island formed by a different generator with a dimension of ≈1.36521 or 3/2 Island formed by using the Sausage as the generator
Island formed by using the Sausage as the generator Anti-island: the generator's symmetry results in the island mirrored
Anti-island: the generator's symmetry results in the island mirrored Quadratic island formed using curves with a different generator
Quadratic island formed using curves with a different generator
See also
Notes
- ^ Quadratic Koch curve type 2
- ^ Quadratic Koch curve type 1
- ^ Neither type 1 nor 2
- This has been called the "zig-zag quadratic Koch snowflake".
References
- Cohen, Nathan (Summer 1995). "Fractal antennas Part 1". Communication Quarterly: 7–23.
- Ghosh, Basudeb; Sinha, Sachendra N.; and Kartikeyan, M. V. (2014). Fractal Apertures in Waveguides, Conducting Screens and Cavities: Analysis and Design, p. 88. Volume 187 of Springer Series in Optical Sciences. ISBN 9783319065359.
- Lauwerier, Hans (1991). Fractals: Endlessly Repeated Geometrical Figures. Translated by Gill-Hoffstädt, Sophia. Princeton University Press. p. 37. ISBN 0-691-02445-6.
The so-called Minkowski sausage. Mandelbrot gave it this name to honor the friend and colleague of Einstein who died so untimely (1864-1909).
- ^ Addison, Paul (1997). Fractals and Chaos: An illustrated course, p. 19. CRC Press. ISBN 0849384435.
- ^ Weisstein, Eric W. (1999). "Minkowski Sausage", archive.lib.msu.edu. Accessed: 21 September 2019.
- ^ Pamfilos, Paris. "Minkowski Sausage", user.math.uoc.gr/~pamfilos/. Accessed: 21 September 2019.
- ^ Weisstein, Eric W. "Minkowski Sausage". MathWorld. Retrieved 22 September 2019.
- Mandelbrot, B. B. (1983). The Fractal Geometry of Nature, p. 48. New York: W. H. Freeman. ISBN 9780716711865. Cited in Weisstein MathWorld.
- Schmidt, Jack (2011). "The Koch snowflake worksheet II", p. 3, UK MA111 Spring 2011, ms.uky.edu. Accessed: 22 September 2019.
External links
- "Square Koch Fractal Curves". Wolfram Demonstrations Project. Retrieved 23 September 2019.
| Fractals | |
|---|---|
| Characteristics | |
| Iterated function system | |
| Strange attractor | |
| L-system | |
| Escape-time fractals | |
| Rendering techniques | |
| Random fractals | |
| People | |
| Other |
|
 . It is therefore often chosen when studying the physical properties of non-integer fractal objects. It is strictly
. It is therefore often chosen when studying the physical properties of non-integer fractal objects. It is strictly