This is an old revision of this page, as edited by Cydebot (talk | contribs) at 15:49, 16 February 2012 (Robot - Speedily moving category Kepler-Poinsot polyhedra to Category:Kepler–Poinsot polyhedra per CFDS.). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 15:49, 16 February 2012 by Cydebot (talk | contribs) (Robot - Speedily moving category Kepler-Poinsot polyhedra to Category:Kepler–Poinsot polyhedra per CFDS.)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff)| Great dodecahedron | |
|---|---|

| |
| Type | Kepler–Poinsot polyhedron |
| Stellation core | regular dodecahedron |
| Elements | F = 12, E = 30 V = 12 (χ = -6) |
| Faces by sides | 12{5} |
| Schläfli symbol | {5,5⁄2} |
| Face configuration | V(5⁄2) |
| Wythoff symbol | 5⁄2 | 2 5 |
| Coxeter diagram | |
| Symmetry group | Ih, H3, , (*532) |
| References | U35, C44, W21 |
| Properties | Regular nonconvex |
 (5)/2 (Vertex figure) |
 Small stellated dodecahedron (dual polyhedron) |
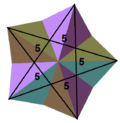
In geometry, the great dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol {5,5/2} and Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), with five pentagons meeting at each vertex, intersecting each other making a pentagrammic path.
. It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), with five pentagons meeting at each vertex, intersecting each other making a pentagrammic path.
Images
| Transparent model | Spherical tiling |
|---|---|
 (With animation) |
 This polyhedron represents a spherical tiling with a density of 3. (One spherical pentagon face is shown above in yellow) |
| Net | Stellation |
 Net for surface geometry |
 It can also be constructed as the second of three stellations of the dodecahedron, and referenced as Wenninger model . |
Related polyhedra
It shares the same edge arrangement as the convex regular icosahedron.
If the great dodecahedron is considered as a properly intersected surface geometry, it has the same topology as a triakis icosahedron with concave pyramids rather than convex ones.
A truncation process applied to the great dodecahedron produces a series of nonconvex uniform polyhedra. Truncating edges down to points produces the dodecadodecahedron as a rectified great dodecahedron. The process completes as a birectification, reducing the original faces down to points, and producing the small stellated dodecahedron.
The truncated small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 pentagonal faces: 12 as the truncation facets of the former vertices, and 12 more (coinciding with the first set) as truncated pentagrams.
| Name | Small stellated dodecahedron | Truncated small stellated dodecahedron | Dodecadodecahedron | Truncated great dodecahedron |
Great dodecahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
|||||
| Picture | 
|

|

|

|

|
Usage
- This shape was the basis for the Rubik's Cube-like Alexander's Star puzzle.
See also
External links
- Weisstein, Eric W., "Great dodecahedron" ("Uniform polyhedron") at MathWorld.
- Uniform polyhedra and duals
- Metal sculpture of Great Dodecahedron
| Star-polyhedra navigator | |
|---|---|
| Kepler-Poinsot polyhedra (nonconvex regular polyhedra) | |
| Uniform truncations of Kepler-Poinsot polyhedra | |
| Nonconvex uniform hemipolyhedra | |
| Duals of nonconvex uniform polyhedra |
|
| Duals of nonconvex uniform polyhedra with infinite stellations | |
| Stellations of the dodecahedron | ||||||
| Platonic solid | Kepler–Poinsot solids | |||||
| Dodecahedron | Small stellated dodecahedron | Great dodecahedron | Great stellated dodecahedron | |||
|---|---|---|---|---|---|---|

|

|

|

| |||

|

|

|

| |||