| Gyrate rhombicosidodecahedron | |
|---|---|
 | |
| Type | Canonical polyhedron Johnson J71 – J72 – J73 |
| Faces | 20 triangles 30 squares 12 pentagons |
| Edges | 120 |
| Vertices | 60 |
| Vertex configuration | |
| Symmetry group | |
| Properties | convex, Rupert property |
| Net | |
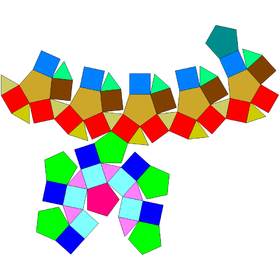 | |
In geometry, the gyrate rhombicosidodecahedron is one of the Johnson solids (J72). It is also a canonical polyhedron.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Construction
The gyrate rhombicosidodecahedron can be constructed similarly as rhombicosidodecahedron: it is constructed from parabidiminished rhombicosidodecahedron by attaching two regular pentagonal cupolas onto its decagonal faces. As a result, these pentagonal cupolas cover its dodecagonal faces, so the resulting polyhedron has 20 equilateral triangles, 30 squares, and 10 regular pentagons as its faces. The difference between those two polyhedrons is that one of two pentagonal cupolas from the gyrate rhombicosidodecahedron is rotated through 36°. A convex polyhedron in which all faces are regular polygons is called the Johnson solid, and the gyrate rhombicosidodecahedron is among them, enumerated as the 72th Johnson solid .

 The difference between rhombicosidodecahedron (left) and gyrate rhombicosidodecahedron (right) by their construction
The difference between rhombicosidodecahedron (left) and gyrate rhombicosidodecahedron (right) by their construction
Properties
Because the two aforementioned polyhedrons have similar construction, they have the same surface area and volume. A gyrate rhombicosidodecahedron with edge length has a surface area by adding all of the area of its faces: Its volume can be calculated by slicing it into two regular pentagonal cupolas and one parabigyrate rhombicosidodecahedron, and adding their volumes:
The gyrate rhombicosidodecahedron is one of the five Johnson solids that do not have Rupert property, meaning a polyhedron of the same or larger size and the same shape as it cannot pass through a hole in it. The other Johnson solids with no such property are parabigyrate rhombicosidodecahedron, metabigyrate rhombicosidodecahedron, trigyrate rhombicosidodecahedron, and paragyrate diminished rhombicosidodecahedron.
See also
Alternative Johnson solids, constructed by rotating different cupolae of a rhombicosidodecahedron, are:
- The parabigyrate rhombicosidodecahedron where two opposing cupolae are rotated;
- The metabigyrate rhombicosidodecahedron where two non-opposing cupolae are rotated;
- And the trigyrate rhombicosidodecahedron where three cupolae are rotated.
References
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ^ Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
- Fredriksson, Albin (2024), "Optimizing for the Rupert property", The American Mathematical Monthly, 131 (3): 255–261, arXiv:2210.00601, doi:10.1080/00029890.2023.2285200.


 .
.
 Its volume can be calculated by slicing it into two regular pentagonal cupolas and one parabigyrate rhombicosidodecahedron, and adding their volumes:
Its volume can be calculated by slicing it into two regular pentagonal cupolas and one parabigyrate rhombicosidodecahedron, and adding their volumes:

 where two opposing cupolae are rotated;
where two opposing cupolae are rotated; where two non-opposing cupolae are rotated;
where two non-opposing cupolae are rotated; where three cupolae are rotated.
where three cupolae are rotated.