| Pentagonal bipyramid | |
|---|---|
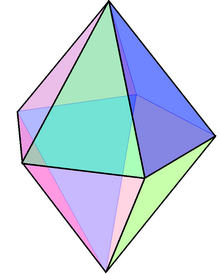 | |
| Type | Bipyramid, Deltahedra Johnson J12 – J13 – J14 |
| Faces | 10 triangles |
| Edges | 15 |
| Vertices | 7 |
| Vertex configuration | |
| Symmetry group | |
| Dihedral angle (degrees) | As a Johnson solid:
|
| Dual polyhedron | pentagonal prism |
| Properties | convex, composite, face-transitive |
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid.
The pentagonal bipyramid may be represented as four-connected well-covered graph. This polyhedron may be used in the chemical compound as the description of an atom cluster known as pentagonal bipyramidal molecular geometry, as a solution in Thomson problem, as well as in decahedral nanoparticles.
Special cases
As a right bipyramid
Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has ten triangles as its faces, fifteen edges, and seven vertices. The pentagonal bipyramid is said to be right if the pyramids are symmetrically regular and both of their apices are on the line passing through the base's center; otherwise, it is oblique.
Like other right bipyramids, the pentagonal bipyramid has three-dimensional symmetry group of dihedral group of order twenty: the appearance is symmetrical by rotating around the axis of symmetry that passing through apices and base's center vertically, and it has mirror symmetry relative to any bisector of the base; it is also symmetrical by reflecting it across a horizontal plane. Therefore, the pentagonal bipyramid is face-transitive or isohedral.
The pentagonal bipyramid is four-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four four-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.
The dual polyhedron of a pentagonal bipyramid is the pentagonal prism. More generally, the dual polyhedron of every bipyramid is the prism, and the vice versa is true. The pentagonal prism has two pentagonal faces at the base, and the rest are five rectangular.
As a Johnson solid

 Pentagonal bipyramid with regular faces, alongside its net.
Pentagonal bipyramid with regular faces, alongside its net.

If the pyramids are regular, all edges of the triangular bipyramid are equal in length, making up the faces equilateral triangles. A polyhedron with only equilateral triangles as faces is called a deltahedron. There are only eight different convex deltahedra, one of which is the pentagonal bipyramid with regular faces. More generally, the convex polyhedron in which all faces are regular is the Johnson solid, and every convex deltahedra is a Johnson solid. The pentagonal bipyramid with the regular faces is among the numbered Johnson solids as , the thirteenth Johnson solid. It is an example of a composite polyhedron because it is constructed by attaching two regular pentagonal pyramids.
A pentagonal bipyramid's surface area is 10 times that of all triangles, and its volume can be ascertained by slicing it into two pentagonal pyramids and adding their volume. In the case of edge length , they are:
The dihedral angle of a pentagonal bipyramid with regular faces can be calculated by adding the angle of pentagonal pyramids:
- the dihedral angle of a pentagonal bipyramid between two adjacent triangles is that of a pentagonal pyramid, approximately 138.2°, and
- the dihedral angle of a pentagonal bipyramid with regular faces between two adjacent triangular faces, on the edge where two pyramids are attached, is 74.8°, obtained by summing the dihedral angle of a pentagonal pyramid between the triangular face and the base.
Applications
In the geometry of chemical compounds, the pentagonal bipyramid can be used as the atom cluster surrounding an atom. The pentagonal bipyramidal molecular geometry describes clusters for which this polyhedron is a pentagonal bipyramid. An example of such a cluster is iodine heptafluoride in the gas phase.
The Thomson problem concerns the minimum-energy configuration of charged particles on a sphere. One of them is a pentagonal bipyramid, a known solution for the case of seven electrons, by placing vertices of a pentagonal bipyramid inscribed in a sphere.
Pentagonal bipyramids and related five-fold shapes are found in decahedral nanoparticles, which can also be macroscopic in size when they are also called fiveling cyclic twins in mineralogy.
References
- Rajwade, A. R. (2001), Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem, Texts and Readings in Mathematics, Hindustan Book Agency, p. 84, doi:10.1007/978-93-86279-06-4, ISBN 978-93-86279-06-4.
- ^ Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- Polya, G. (1954), Mathematics and Plausible Reasoning: Induction and analogy in mathematics, Princeton University Press, p. 138, ISBN 0-691-02509-6.
- Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. p. 403. ISBN 978-1-285-19569-8.
- McLean, K. Robin (1990), "Dungeons, dragons, and dice", The Mathematical Gazette, 74 (469): 243–256, doi:10.2307/3619822, JSTOR 3619822, S2CID 195047512.
- Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.
- Montroll, John (2011), Origami Polyhedra Design, CRC Press, p. 5, ISBN 978-1-4398-7106-5.
- Goldberg, Nicholas; Haylett, Christine (2019), Oxford Mathematics for the Caribbean: Book 1 (6th ed.), Oxford University Press, ISBN 978-0-19-842569-4.
- Trigg, Charles W. (1978), "An infinite class of deltahedra", Mathematics Magazine, 51 (1): 55–57, doi:10.1080/0025570X.1978.11976675, JSTOR 2689647, MR 1572246.
- Uehara, Ryuhei (2020), Introduction to Computational Origami: The World of New Computational Geometry, Springer, doi:10.1007/978-981-15-4470-5, ISBN 978-981-15-4470-5, S2CID 220150682.
- Timofeenko, A. V. (2009), "Convex Polyhedra with Parquet Faces" (PDF), Docklady Mathematics, 80 (2): 720–723, doi:10.1134/S1064562409050238.
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603.
- Gillespie, Ronald J.; Hargittai, István (2013), The VSEPR Model of Molecular Geometry, Dover Publications, p. 152, ISBN 978-0-486-48615-4.
- Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete & Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734, S2CID 26955765.
- Marks, L. D.; Peng, L. (2016), "Nanoparticle shape, thermodynamics and kinetics", Journal of Physics: Condensed Matter, 28 (5): 053001, Bibcode:2016JPCM...28e3001M, doi:10.1088/0953-8984/28/5/053001, ISSN 0953-8984, PMID 26792459.
- Rose, Gustav (1831), "Ueber die Krystallformen des Goldes und des Silbers", Annalen der Physik, 99 (10): 196–204, Bibcode:1831AnP....99..196R, doi:10.1002/andp.18310991003, ISSN 0003-3804.
External links
- Weisstein, Eric W., "Pentagonal dipyramid" ("Dipyramid") at MathWorld.
- Conway Notation for Polyhedra Try: dP5


 , the thirteenth Johnson solid. It is an example of a
, the thirteenth Johnson solid. It is an example of a  is 10 times that of all triangles, and its volume
is 10 times that of all triangles, and its volume  can be ascertained by slicing it into two pentagonal pyramids and adding their volume. In the case of edge length
can be ascertained by slicing it into two pentagonal pyramids and adding their volume. In the case of edge length  , they are:
, they are:
