Misplaced Pages

Pentagonal pyramid
Type	Pyramid Johnson J1 – J2 – J3
Faces	5 triangles 1 pentagon
Edges	10
Vertices	6
Vertex configuration	${\displaystyle 5\times (3^{2}\times 5)+1\times 3^{5}}$
Symmetry group	${\displaystyle C_{5\mathrm {v} }}$
Dihedral angle (degrees)	As a Johnson solid: triangle-to-triangle: 138.19° triangle-to-pentagon: 37.37°
Dual polyhedron	self-dual
Properties	convex, elementary (Johnson solid)
Net

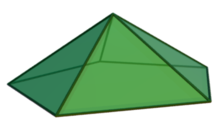
In geometry, a pentagonal pyramid is a pyramid with a pentagon base and five triangular faces, having a total of six faces. It is categorized as a Johnson solid if all of the edges are equal in length, forming equilateral triangular faces and a regular pentagonal base.

Pentagonal pyramids occur as pieces and tools in the construction of many polyhedra. They also appear in the field of natural science, as in stereochemistry where the shape can be described as the pentagonal pyramidal molecular geometry, as well as the study of shell assembling in the underlying potential energy surfaces and disclination in fivelings and related shapes such as pyramidal copper and other metal nanowires.

Properties

A pentagonal pyramid has six vertices, ten edges, and six faces. One of its faces is pentagon, a base of the pyramid; five others are triangles. Five of the edges make up the pentagon by connecting its five vertices, and the other five edges are known as the lateral edges of the pyramid, meeting at the sixth vertex called the apex. A pentagonal pyramid is said to be regular if its base is circumscribed in a circle that forms a regular pentagon, and it is said to be right if its altitude is erected perpendicularly to the base's center.

Like other right pyramids with a regular polygon as a base, this pyramid has pyramidal symmetry of cyclic group ${\displaystyle C_{5\mathrm {v} }}$: the pyramid is left invariant by rotations of one, two, three, four-fifths around its axis of symmetry, the line connecting the apex to the center of the base. It is also mirror symmetric relative to any perpendicular plane passing through a bisector of the base. It can be represented as the wheel graph ${\displaystyle W_{5}}$, meaning its skeleton can be interpreted as a pentagon in which its five vertices connects a vertex in the center called the universal vertex. It is self-dual, meaning its dual polyhedron is the pentagonal pyramid itself.

When all edges are equal in length, the five triangular faces are equilateral and the base is a regular pentagon. Because this pyramid remains convex and all of its faces are regular polygons, it is classified as the second Johnson solid ${\displaystyle J_{2}}$. The dihedral angle between two adjacent triangular faces is approximately 138.19° and that between the triangular face and the base is 37.37°. It is an elementary polyhedron, meaning that it cannot be separated by a plane to create two small convex polyhedrons with regular faces. A polyhedron's surface area is the sum of the areas of its faces. Therefore, the surface area of a pentagonal pyramid is the sum of the areas of the four triangles and the one pentagon. The volume of every pyramid equals one-third of the area of its base multiplied by its height. So, the volume of a pentagonal pyramid is one-third of the product of the height and a pentagonal pyramid's area. In the case of Johnson solid with edge length ${\displaystyle a}$, its surface area ${\displaystyle A}$ and volume ${\displaystyle V}$ are: $${\displaystyle {\begin{aligned}A&={\frac {a^{2}}{2}}{\sqrt {{\frac {5}{2}}\left(10+{\sqrt {5}}+{\sqrt {75+30{\sqrt {5}}}}\right)}}\approx 3.88554a^{2},\\V&={\frac {5+{\sqrt {5}}}{24}}a^{3}\approx 0.30150a^{3}.\end{aligned}}}$$

Applications

Pentagonal pyramids can be found as components of many polyhedrons. Attaching its base to the pentagonal face of another polyhedron is an example of the construction process known as augmentation, and attaching it to prisms or antiprisms is known as elongation or gyroelongation, respectively. Examples of polyhedrons are the pentakis dodecahedron is constructed from the dodecahedron by attaching the base of pentagonal pyramids onto each pentagonal face, small stellated dodecahedron is constructed from a regular dodecahedron stellated by pentagonal pyramids, and a regular icosahedron constructed from a pentagonal antiprism by attaching two pentagonal pyramids onto its pentagonal bases. Some Johnson solids are constructed by either augmenting pentagonal pyramids or augmenting other shapes with pentagonal pyramids: an elongated pentagonal pyramid ${\displaystyle J_{9}}$, a gyroelongated pentagonal pyramid ${\displaystyle J_{11}}$, a pentagonal bipyramid ${\displaystyle J_{13}}$, an elongated pentagonal bipyramid ${\displaystyle J_{16}}$, an augmented dodecahedron ${\displaystyle J_{58}}$, a parabiaugmented dodecahedron ${\displaystyle J_{59}}$, a metabiaugmented dodecahedron ${\displaystyle J_{60}}$, and a triaugmented dodecahedron ${\displaystyle J_{61}}$. Relatedly, the removal of a pentagonal pyramid from polyhedra is an example of a technique known as diminishment; the metabidiminished icosahedron ${\displaystyle J_{62}}$ and tridiminished icosahedron ${\displaystyle J_{63}}$ are the examples in which their constructions begin by removing pentagonal pyramids from a regular icosahedron.

In stereochemistry, an atom cluster can have a pentagonal pyramidal geometry. This molecule has a main-group element with one active lone pair of electrons, which can be described by a model that predicts the geometry of molecules known as VSEPR theory. An example of a molecule with this structure is nido-cage carbonate CB₅H₉.

Fejer et al. (2009) modeled the formation of virus shells, known as capsids, from pieces shaped like pentagonal and hexagonal pyramids. These shapes were chosen to resemble those of the protein subunits of natural viruses. By appropriately choosing the attractive and repulsive forces between pyramids, they found that the pyramids could self-assemble into icosahedral shells reminiscent of those found in nature.

Gryzunova (2017) studied the relaxation of internal elastic stress fields due to disclinations in twinned copper particles. Such a shape is the pentagonal pyramid, which allows growth to a large size and preserves symmetry. This can be done by activating cathode by the process of initial crystal growth in the electrolyte, by the movement of aluminum and silicon oxides' abrasive particles.

References

Notes

1. ^ Johnson (1966).
2. • Ball & Coxeter (1987), p. 130
   • Grgić et al. (2022), p. 476
3. Smith (2000), p. 98.
4. • Calter & Calter (2011), p. 198
   • Polya (1954), p. 138
5. Pisanski & Servatius (2013), p. 21.
6. Wohlleben (2019), p. 485–486.
7. Uehara (2020), p. 62.
8. • Hartshorne (2000), p. 464
   • Johnson (1966)
9. Calter & Calter (2011), p. 198.
10. Berman (1971).
11. Slobodan, Obradović & Ðukanović (2015).
12. • Çolak & Gelişgen (2015)
    • Kappraff (2001), p. 309
    • Silvester (2001), p. 140–141
13. Rajwade (2001), pp. 84–88. See Table 12.3, where ${\displaystyle P_{n}}$ denotes the ${\displaystyle n}$-sided prism and ${\displaystyle A_{n}}$ denotes the ${\displaystyle n}$-sided antiprism.
14. Gailiunas (2001).
15. Petrucci, Harwood & Herring (2002), p. 414.
16. Macartney (2017), p. 482.
17. Fejer et al. (2009).
18. Gryzunova (2017).

Works cited

• Ball, W. W. R.; Coxeter, H. S. M. (1987). Mathematical Recreations and Essays. Dover Publications. ISBN 978-0-486-25357-2.
• Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
• Calter, Paul A.; Calter, Michael A. (2011). Technical Mathematics. John Wiley & Sons. ISBN 978-0-470-53492-2.
• Çolak, Zeynep; Gelişgen, Özcan (2015). "New Metrics for Deltoidal Hexacontahedron and Pentakis Dodecahedron". Sakarya University Journal of Science. 19 (3): 353–360. doi:10.16984/saufenbilder.03497.
• Fejer, Szilard N.; James, Tim R. James; Hernández-Rojasc, Javier; Wales, David J. (2009). "Energy landscapes for shells assembled from pentagonal and hexagonal pyramids". Physical Chemistry Chemical Physics. 11: 2098–2104. doi:10.1039/B818062H.
• Gailiunas, Paul (2001). "A Polyhedral Byway" (PDF). In Sarhangi, Reza; Jablan, Slavik (eds.). Bridges: Mathematical Connections in Art, Music, and Science (Thesis). Bridges Conference. pp. 115–122.
• Grgić, Ivan; Karakašić, Mirko; Ivandić, Željko; Glavaš, Hrvoje (2022). "Maintaining the Descriptive Geometry's Design Knowledge". In Glavaš, Hrvoje; Hadzima-Nyarko, Marijana; Karakašić, Mirko; Ademović, Naida; Avdaković, Samir (eds.). 30th International Conference on Organization and Technology of Maintenance (OTO 2021): Proceedings of 30th International Conference on Organization and Technology of Maintenance (OTO 2021). International Conference on Organization and Technology of Maintenance. doi:10.1007/978-3-030-92851-3.
• Gryzunova, N. N. (2017). "К вопросу о дисклинационной природе пентагональных пирамид с высокими ступенями роста электролитического происхождения" [On the disclination nature of pentagonal pyramids with high growth steps of electrolytic origin]. Letters on Materials (in Russian). 7 (1): 39–43. doi:10.22226/2410-3535-2017-1-39-43.
• Hartshorne, Robin (2000). Geometry: Euclid and Beyond. Undergraduate Texts in Mathematics. Springer-Verlag. ISBN 9780387986500.
• Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
• Kappraff, Jay (2001). Connections: The Geometric Bridge Between Art and Science (2nd ed.). World Scientific. ISBN 981-02-4585-8.
• Macartney, D. H. (2017). "Cucurbiturils in Drug Binding and Delivery". In Gokel, George W.; Barbour, Leonard J. (eds.). Comprehensive Supramolecular Chemistry II. Elsevier. ISBN 978-0-12-803198-8.
• Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry: Principles and Modern Applications. Vol. 1. Prentice Hall. ISBN 9780130143297.
• Pisanski, Tomaž; Servatius, Brigitte (2013). Configuration from a Graphical Viewpoint. Springer. doi:10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4.
• Polya, G. (1954). Mathematics and Plausible Reasoning: Induction and analogy in mathematics. Princeton University Press. ISBN 0-691-02509-6.
• Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
• Silvester, John R. (2001). Geometry: Ancient and Modern. Oxford University Publisher.
• Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms" (PDF). Journal for Geometry and Graphics. 19 (1): 79–91.
• Smith, James T. (2000). Methods of Geometry. John Wiley & Sons. ISBN 0-471-25183-6.
• Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5.
• Wohlleben, Eva (2019). "Duality in Non-Polyhedral Bodies Part I: Polyliner". In Cocchiarella, Luigi (ed.). ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary - Milan, Italy, August 3-7, 2018. International Conference on Geometry and Graphics. Springer. doi:10.1007/978-3-319-95588-9. ISBN 978-3-319-95588-9.

External links

• Weisstein, Eric W., "Pentagonal pyramid" ("Johnson solid") at MathWorld.
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRML model)

• Elementary polyhedron
• Johnson solids
• Prismatoid polyhedra
• Pyramids (geometry)
• Self-dual polyhedra